フォロワー2700人突破記念問題の解答
はじめに
この記事は、最近twitterで公開した次の問題の解答について解説します。
フォロワー$2700$人突破記念問題!
— apu (@apu_yokai) December 29, 2021
図のように正三角形の辺を$31$等分した点と頂点をつなぐ線分を引き、正三角形の内部の交点の数を$A$とします。同様に正三角形の辺を$32$等分した点と頂点をつなぐ線分を引き、正三角形の内部の交点の数を$B$とします。
$B-A$はいくつ? pic.twitter.com/OyH8MkT3HA
図のように正三角形の辺を$31$等分した点と頂点をつなぐ線分を引き、正三角形の内部の交点の数を$A$とします。同様に正三角形の辺を$32$等分した点と頂点をつなぐ線分を引き、正三角形の内部の交点の数を$B$とします。
$B-A$はいくつ?
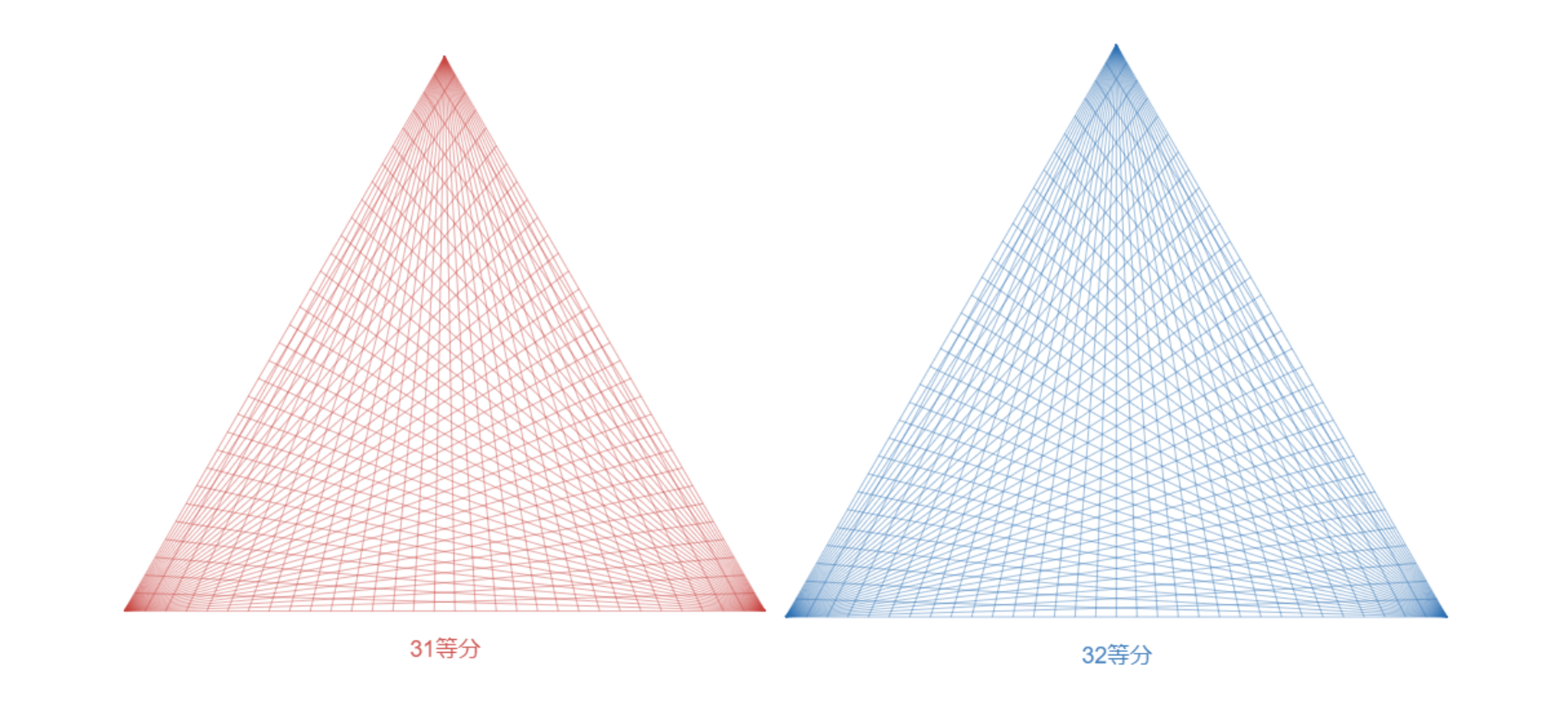 問題
問題
この記事では、正三角形の辺を$n$等分した点と頂点をつなぐ線分を引いたときの正三角形の内部の交点の数を $T(n)$ で表すことにします。
そうすると、
$A=T(31),B=T(32)$
ですから、
$B-A=T(32)-T(31)$
を求めることになります。
観察
いきなり解いてもいいのですが、小さい数から試してみると、ちょっと面白い現象が起きることに気が付きます。
小さい数から試してみる
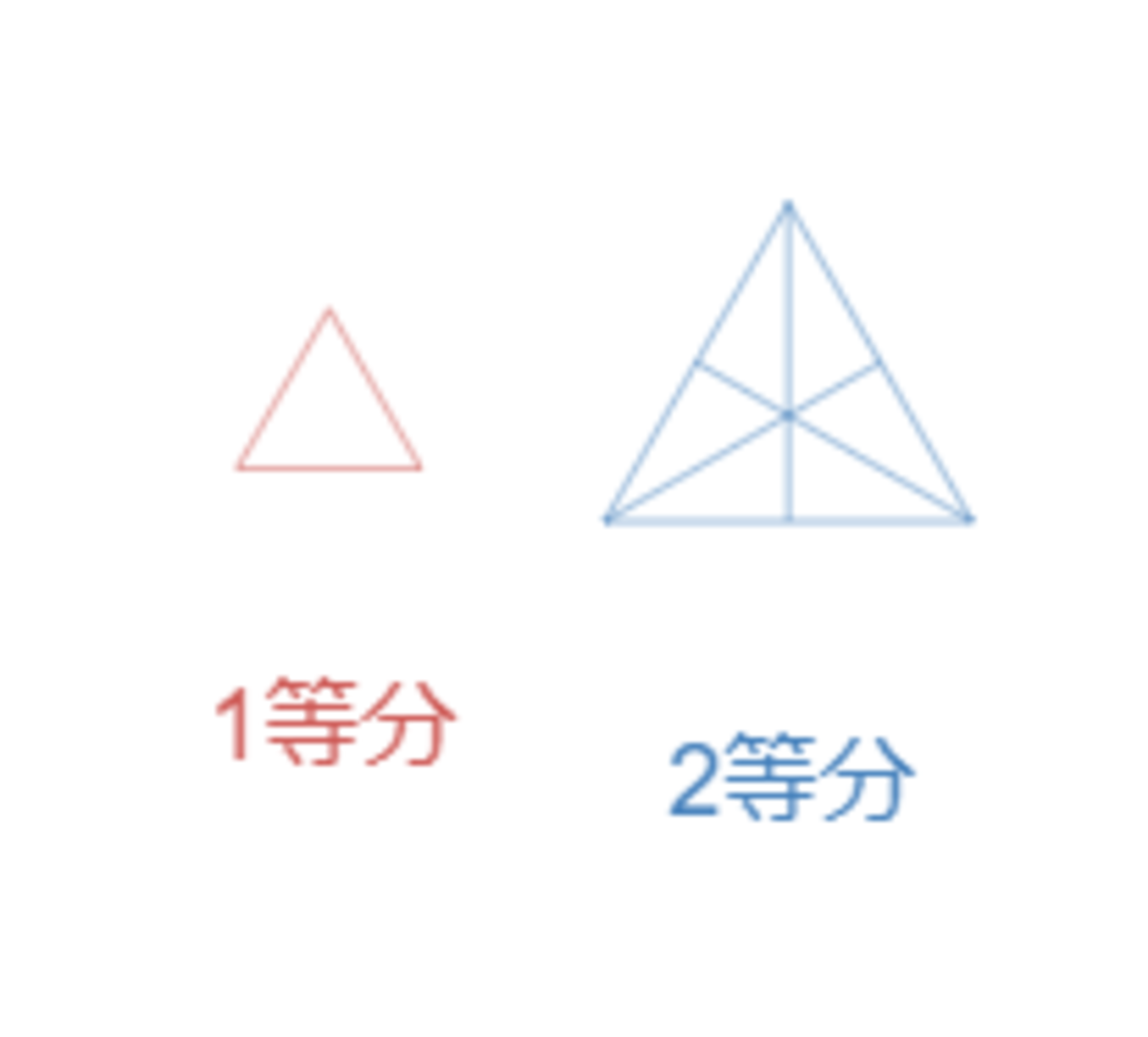 1等分(0点)・2等分(1点)
1等分(0点)・2等分(1点)
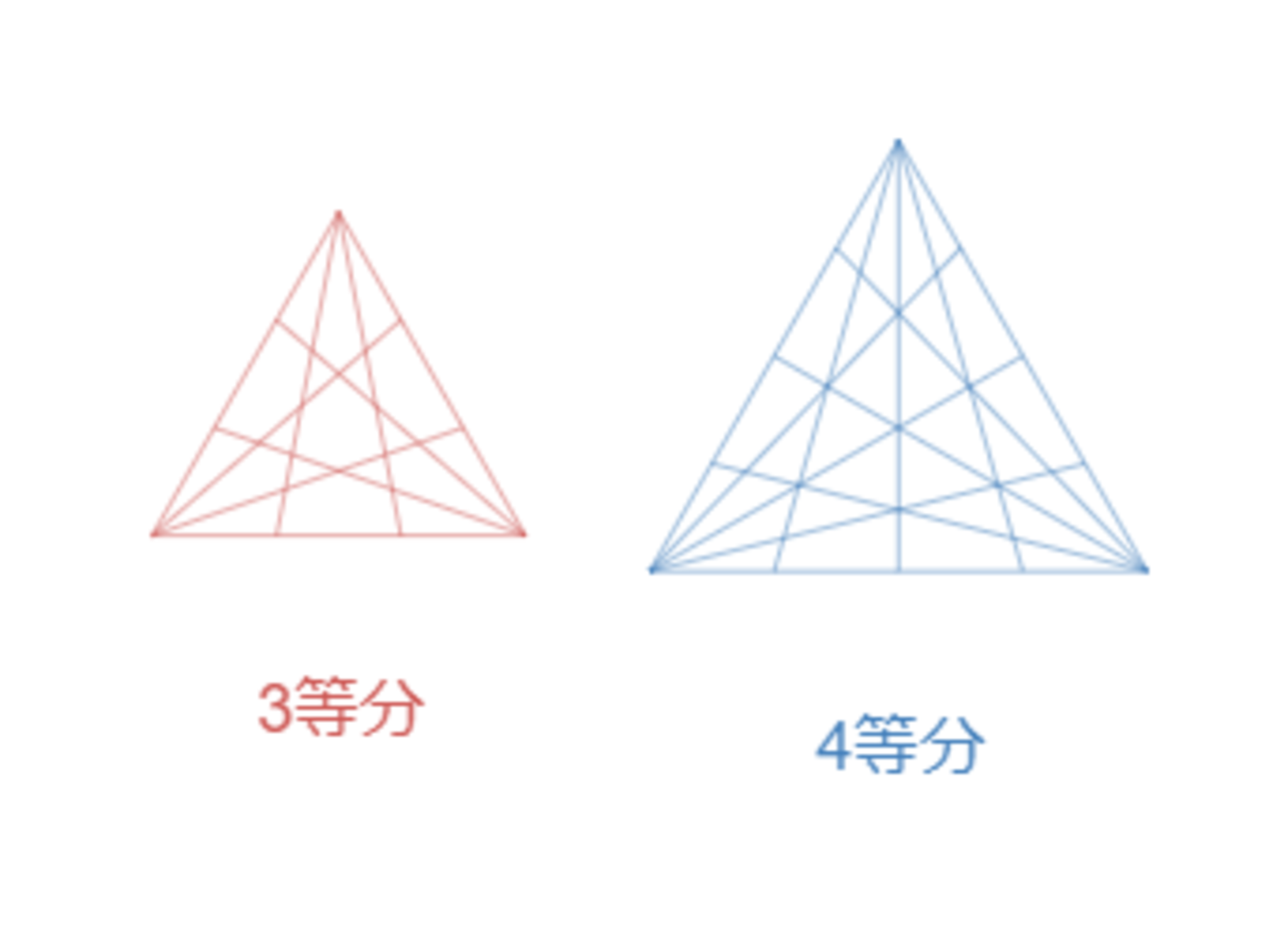 3等分(12点)・4等分(13点)
3等分(12点)・4等分(13点)
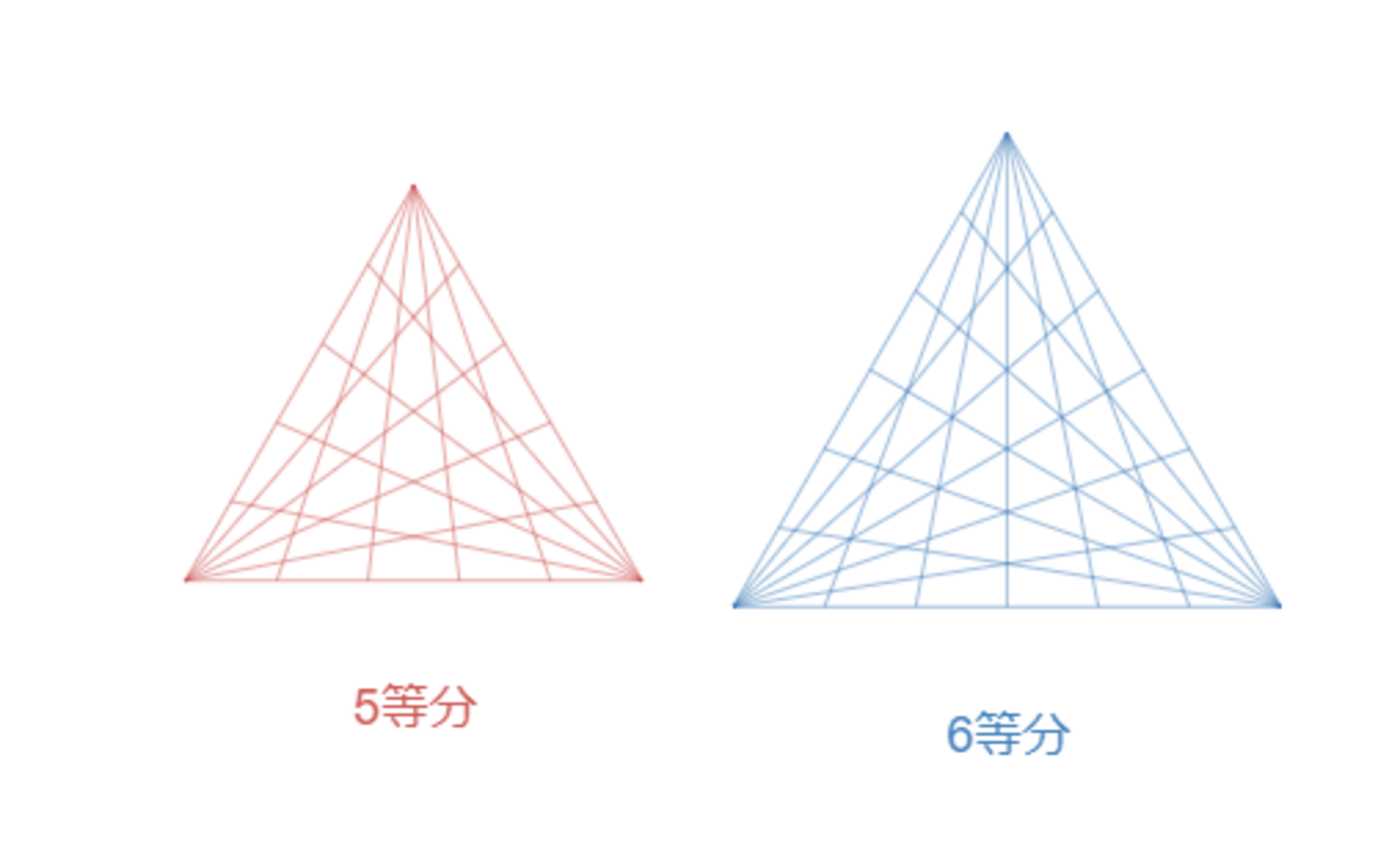 5等分(48点)・6等分(49点)
5等分(48点)・6等分(49点)
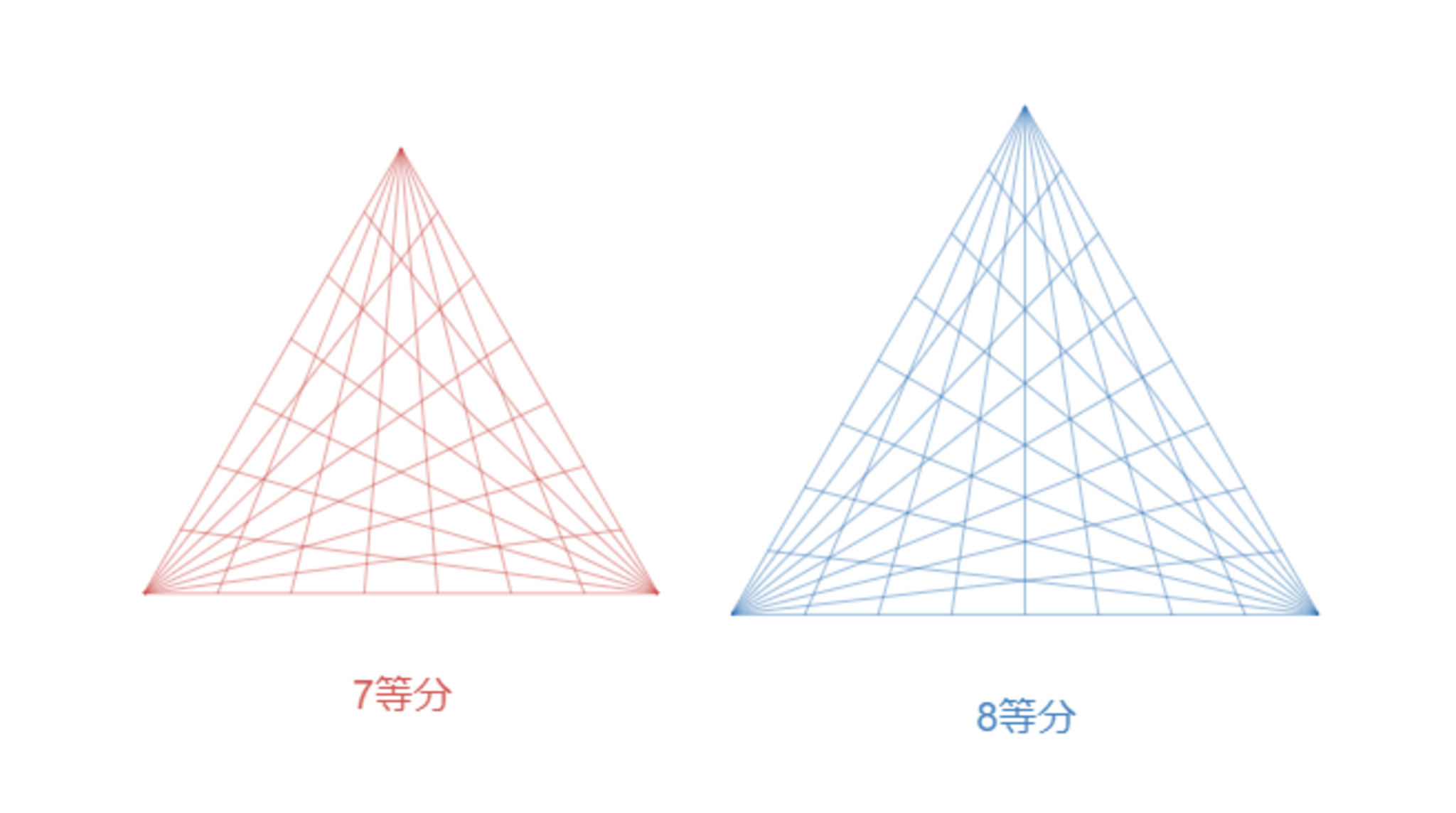 7等分(108点)・8等分(109点)
7等分(108点)・8等分(109点)
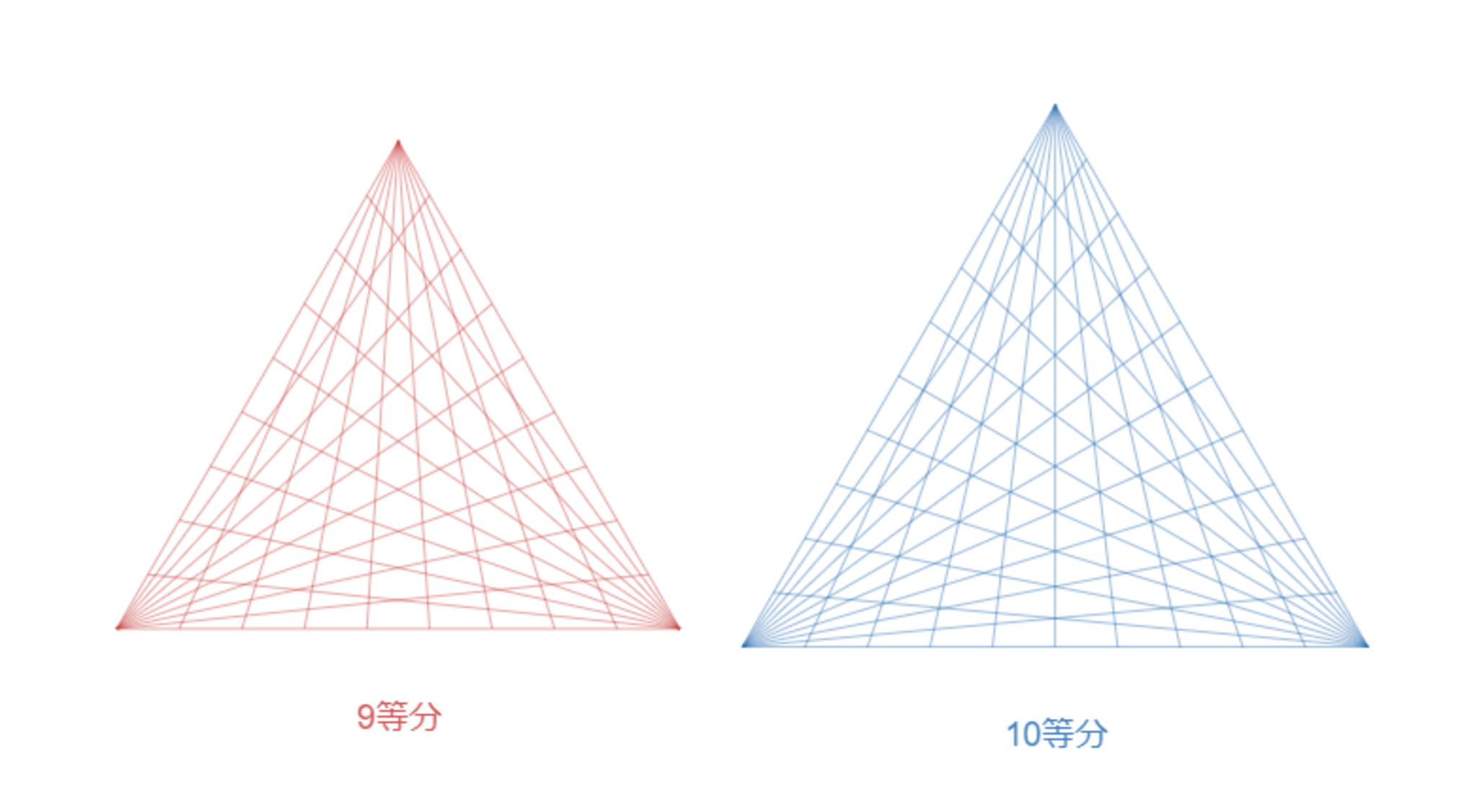 9等分(192点)・10等分(193点)
9等分(192点)・10等分(193点)
ここまでの結果を表にしてみましょう。
| $n$ | $T(n)$ |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 3 | 12 |
| 4 | 13 |
| 5 | 48 |
| 6 | 49 |
| 7 | 108 |
| 8 | 109 |
| 9 | 192 |
| 10 | 193 |
ここまでは全部、$T(2n)=T(2n-1)+1$ という法則が成り立っていることに気が付きます。
そうすると、この後もずっとこの法則が成り立つのではないか、と予想できます。
実際にはどうなんでしょうか?
例外もある
残念ながら、$n$が小さい場合は $T(2n)=T(2n-1)+1$ が成立していますが、$n$ が大きくなってくるとこの法則が成り立たないケースが出てきてしまいます。
最初の例外は $T(15)=576,T(16)=589$ の組合せです。
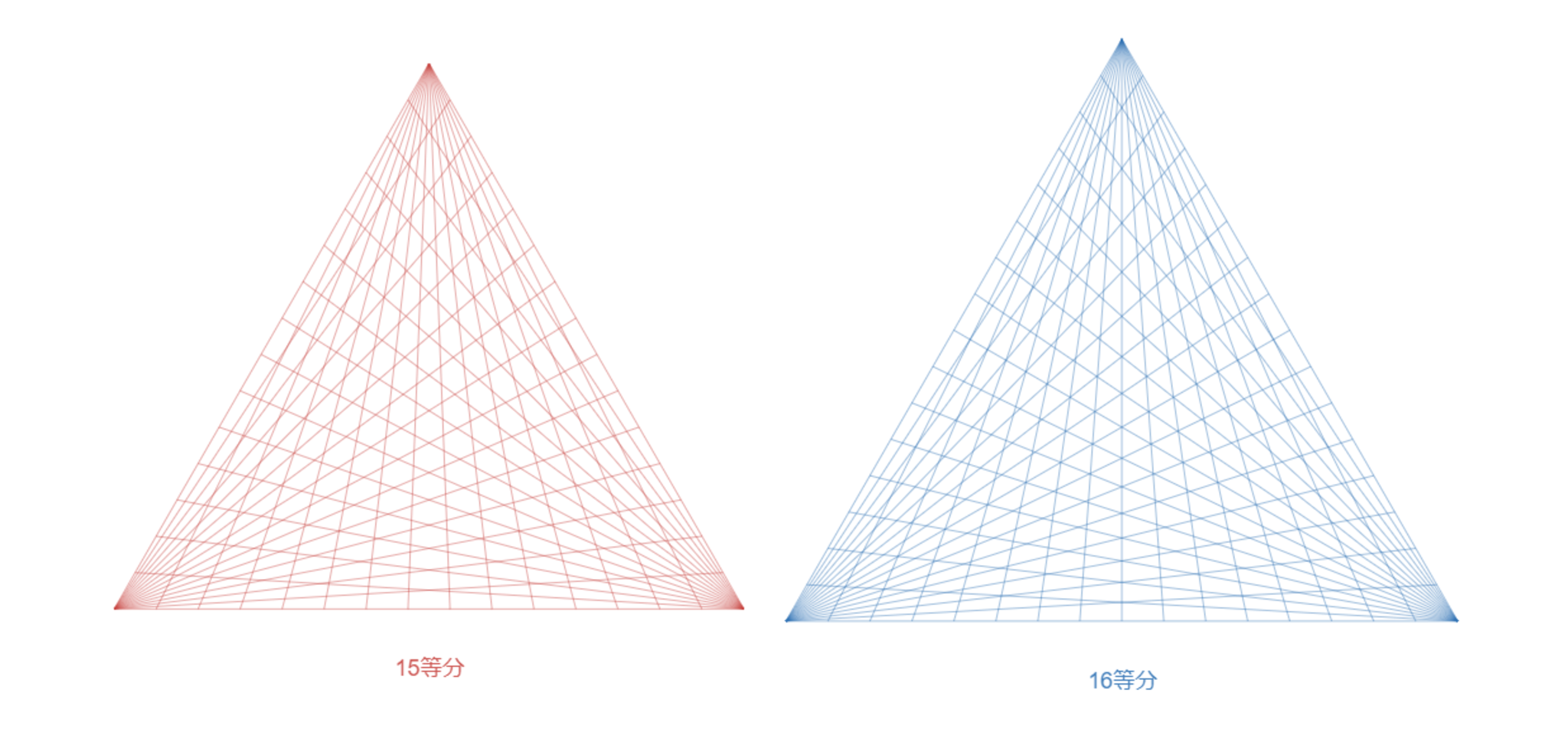 15等分(576点)・16等分(589点)
15等分(576点)・16等分(589点)
3つの線分がが1点で集まる数を数える
あらためて、問題を解くための方針を考えます。
まず、異なる頂点を通る線分を$2$本選ぶと、その$2$本の線分は正三角形の内部で交点を持ちます。
それぞれの頂点からは $n-1$ 本の線分が引かれていますので、2つの頂点からの線分の選び方の組合せは $(n-1)^2$ となります。
$n$等分の場合の$2$本の線分の選び方の場合の数を $T_2(n)$ で表すことにしましょう。対称性を考えると、
$T_2(n)=3(n-1)^2$
となります。
正三角形内部の交点には、$2$つの線分が$1$ 点で交わる場合のほか、$3$つの線分が$1$点で交わる場合がありますが、$T_ 2(n)$ ではそのような点を$3$回カウントしていることになります。
そこで、$n$等分の場合の$3$本の線分が$1$点で交わる交点の数を $T_3(n)$ で表すことにすると、次のように表すことができます。
$T(n)=T_2(n)-2\,T_3(n)$
$15$等分、$16$等分の場合で確認してみましょう。
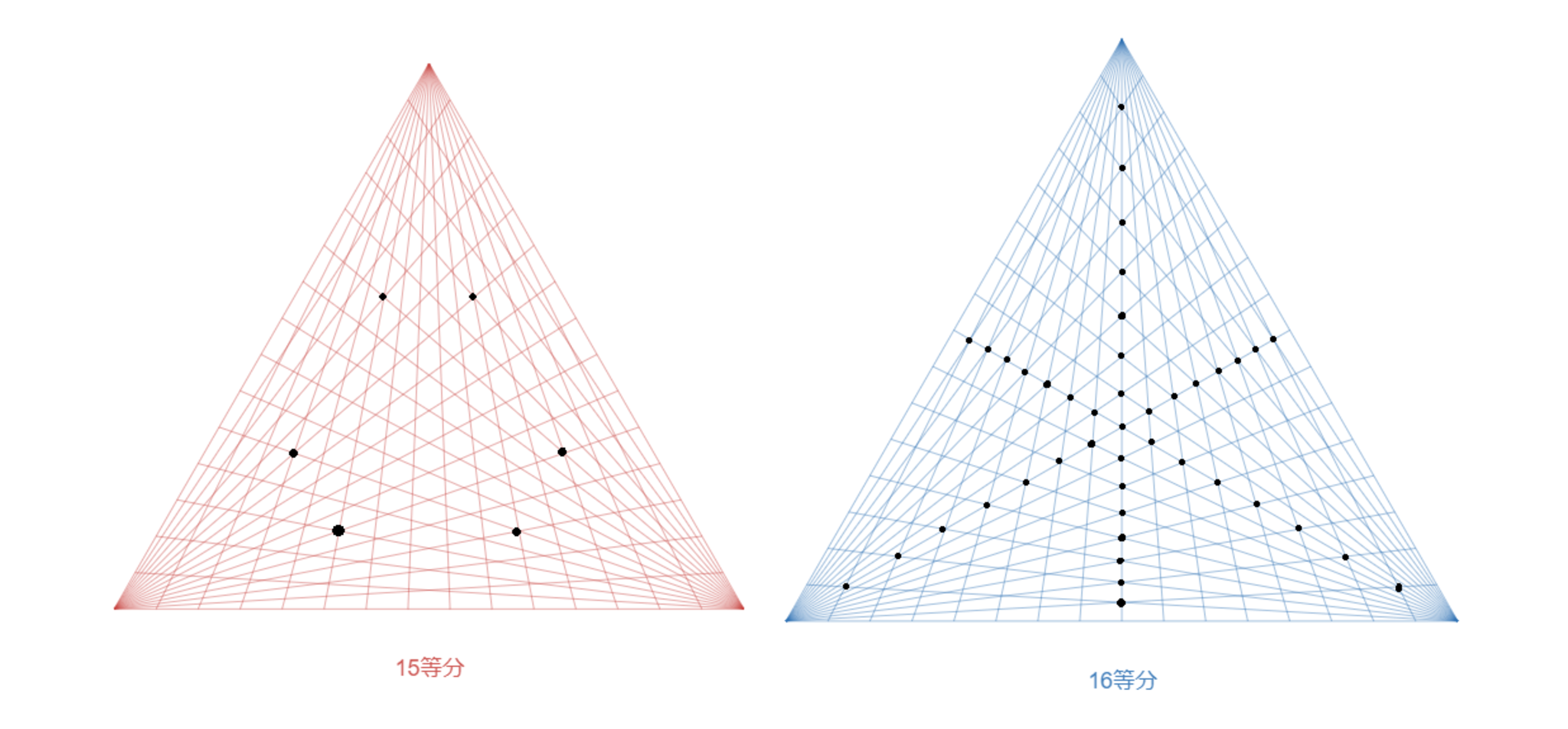 3つの線分が1点で集まる位置
3つの線分が1点で集まる位置
| $n$ | 15 | 16 |
|---|---|---|
| $T(n)$ | 576 | 589 |
| $T_2(n)$ | 588 | 675 |
| $T_3(n)$ | 6 | 43 |
$T(n)=T_2(n)-2\,T_3(n)$ が確かに成り立っていますね!
チェバの定理
しかし、3つの線分が1点で交わっているかどうかを確かめるにはどうすればいいのでしょうか。
それには、チェバの定理を使うのが便利です。
三角形$ABC$において、三角形の内部に任意の点$O$をとり、直線$AO$と$BC$、$BO$と$CA$、$CO$と$AB$の交点をそれぞれ$D$、$E$、$F$とする。この時、次の等式が成立する。なお、点$O$は、三角形の内部にあっても外部にあってもよい。
${\displaystyle {AF \over FB}\cdot {BD \over DC}\cdot {CE \over EA}=1}$
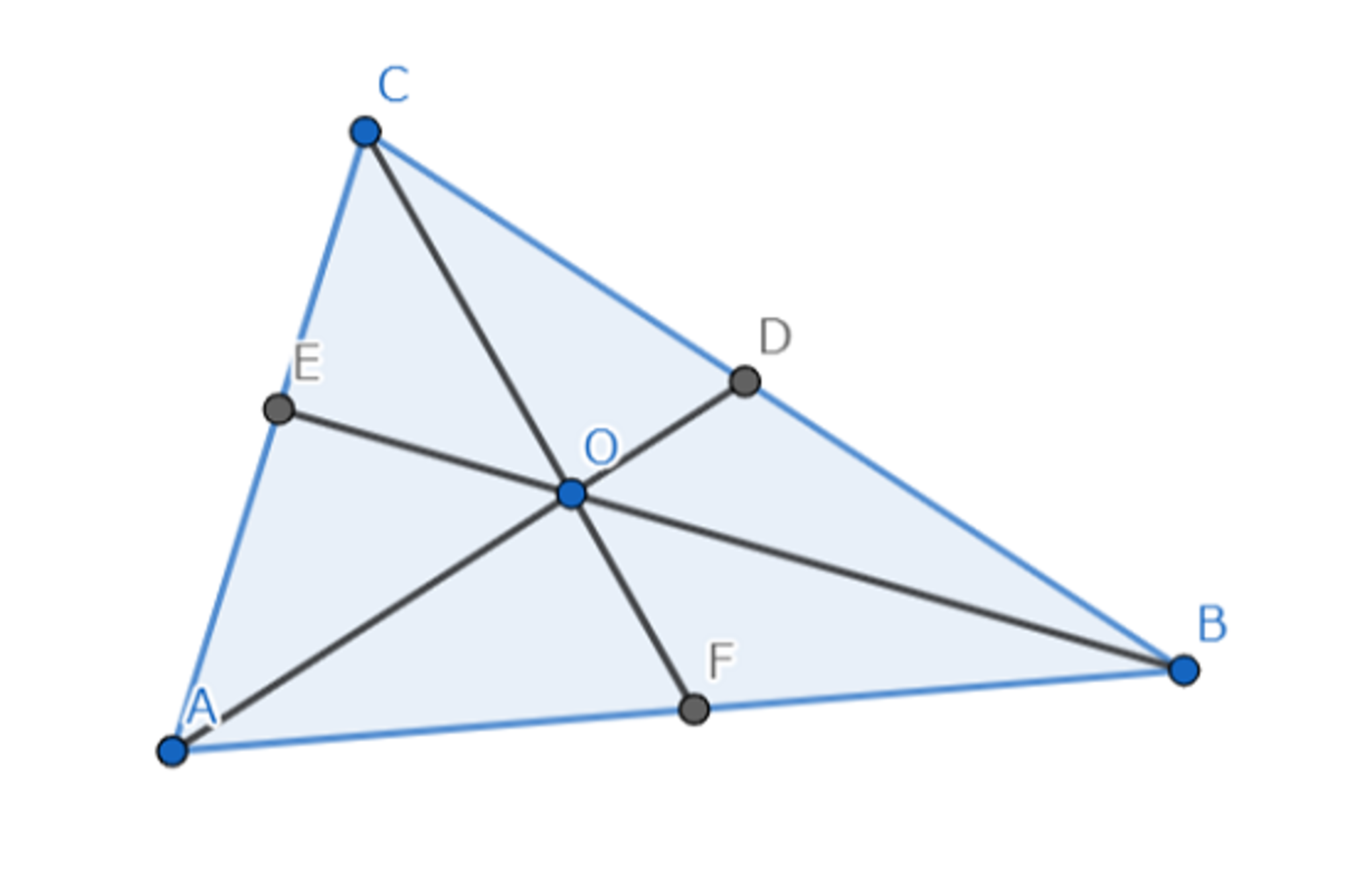 チェバの定理
チェバの定理
具体的に求める
準備が整ったので、後は計算を進めましょう。
重複を含めた$2$線分の交点の数
$T_2(31)$ を計算する
$T_2(31)=3(31-1)^2=2700$
$T_2(32)$ を計算する
$T_2(32)=3(32-1)^2=2883$
$3$線分の交点の数
$T_3(31)$ を計算する
チェバの定理により、$T_3(31)$ は
$\dfrac{i}{31-i}\cdot\dfrac{j}{31-j}=\dfrac{k}{31-k}$
となるような$1$ 以上 $30$ 以下の $i,j,k$ の組合せの場合の数と同じになります。
対称性を考えて、$j,j$について $1$ 以上 $15$ 以下の整数について調べれば十分です。
![!FORMULA[76][836579695][0] について調べる](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20211231190203.png?alt=media) $i=1\cdots15,j=1\cdots15$ について調べる
$i=1\cdots15,j=1\cdots15$ について調べる
しらみつぶしに調べてみると、条件を満たす組み合わせは存在しないことがわかります。
$T_3(31)=0$
$T_3(32)$ を計算する
チェバの定理により、$T_3(32)$ は
$\dfrac{i}{32-i}\cdot\dfrac{j}{32-j}=\dfrac{k}{32-k}$
となるような$1$ 以上 $31$ 以下の $i,j,k$ の組合せを探します。
対称性を考えて、$j,j$について $1$ 以上 $16$ 以下の整数について調べれば十分です。
![!FORMULA[87][331021101][0] について調べる](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20211231190255.png?alt=media) $i=1\cdots16,j=1\cdots16$ について調べる
$i=1\cdots16,j=1\cdots16$ について調べる
しらみつぶしに調べてみると、条件を満たす組み合わせは次のとおりです。
$\dfrac{1}{31}\cdot\dfrac{16}{16}=\dfrac{1}{31}$
$\dfrac{2}{30}\cdot\dfrac{16}{16}=\dfrac{2}{30}$
$\dfrac{3}{29}\cdot\dfrac{16}{16}=\dfrac{3}{29}$
$\qquad\vdots$
$\dfrac{15}{17}\cdot\dfrac{16}{16}=\dfrac{15}{17}$
$\dfrac{16}{16}\cdot\dfrac{1}{31}=\dfrac{1}{31}$
$\dfrac{16}{16}\cdot\dfrac{2}{30}=\dfrac{2}{30}$
$\dfrac{16}{16}\cdot\dfrac{3}{29}=\dfrac{3}{29}$
$\qquad\vdots$
$\dfrac{16}{16}\cdot\dfrac{16}{16}=\dfrac{16}{16}$
正三角形の中心に$1$個と、辺の中点を通る線分上に$15\cdot2=30$個となります。
対称性から、交点の数は全部で
$T_3(32)=30\cdot3+1=91$
とわかります。
交点の数
以上より
31等分の場合の交点の数
$A=T(31)=T_2(31)-2\,T_3(31)=2700-2\cdot0=2700$
32等分の場合の交点の数
$B=T(32)=T_2(32)-2\,T_3(32)=2883-2\cdot91=2701$
したがって求める交点の差は
$\therefore B=A=2701-2700=1$
というわけで、答えは1でした!
おわりに
今回は、フォロワー$2700$人記念ということで、$2700$にちなんだ問題をつくってみたというわけでした。
答えの図
— apu (@apu_yokai) December 30, 2021
A=2700
B=2701
で、問題の答えは
B-A=1
でした!
2700を超えたのも、1人1人のフォローのおかげです!
今後ともよろしくお願いします!🙇♂️ pic.twitter.com/VCS3tEsS36
$31$等分のときは交点が$2700$個、$32$等分のときは交点が$2701$個になるのですが、交差する$2$本の線分の組合せは$183$個も増えるのに、交点は $1$個しか増えないのってちょっとおもしろくないですか?
なお、この記事は$2022$年$1$月$1$日に公開しました。
$1$月$1$日に答えが$1$になる問題の解説を公開することができて、なんだかとても縁起がいい気がしますね!
あけましておめでとうございます。
今年もよろしくお願いします!
