Fibonacci 数を含む無限連分数
連分数-9
前提知識 : 特に無し.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
Fibonacci 数
お久振りです. 今回の記事は, 以前に見付けたとある連分数のご紹介になります.
通例に従い, Fibonacci 数列$(F_n)_{n\in\mathbb{Z}}$を
\begin{align}
F_0=0,\ F_1=1,\ F_{n+2}=F_{n+1}+F_n
\end{align}
の漸化式によって定義する. 即ち Fibonacci 数列とは, このような整数の羅列である.
\begin{align}
\ldots\ 0,\ 1,\ 1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34,\ 55,\ 89,\ 144,\ \ldots.
\end{align}
あらゆる整数$m,\ n$にたいして, 等式$F_{m+n+1}=F_{m+1}F_{n+1}+F_mF_n$が成立つ.
帰納法に依る (略).
あらゆる整数$l,\ m,\ n$にたいして, 等式$F_{n+l}F_{n+m}-F_nF_{n+l+m}=(-1)^nF_lF_m$が成立つ.
代りに, 命題
\begin{align}
a+b=c+d\Longrightarrow F_aF_b-F_cF_d=(-1)^n\left(F_{a-n}F_{b-n}-F_{c-n}F_{d-n}\right)
\end{align}
を証明する. $n=1$および$n=-1$にたいしては, この等式は加法定理から自明に成立し, また$|n|\neq1$なる場合には, $n=1$あるいは$n=-1$に対応する命題を繰返し適用すれば証明がなされる. 故にこの命題は真であり, これに$a=n+l,\ $$b=n+m,\ $$c=n,\ $$d=n+l+m$を代入すれば
\begin{align}
F_{n+l}F_{n+m}-F_nF_{n+l+m}=(-1)^n\left(F_lF_m-F_0F_{l+m}\right)=(-1)^nF_lF_m
\end{align}
を得て, 示すべき等式に達する. $\quad\Box$
あらゆる整数$n$にたいして, 等式$F_n^4-1=F_{n+2}F_{n+1}F_{n-1}F_{n-2}$が成立つ
先の命題の系として
\begin{align}
&F_{n+1}F_{n-1}-F_n^2=(-1)^n,\\
&F_{n+2}F_{n-2}-F_n^2=-(-1)^n
\end{align}
の二式が成立する. これを用いれば, $F_n^4-1$は
\begin{align}
F_n^4-1&=(F_n^2+(-1)^n)(F_n^2-(-1)^n)\\
&=F_{n+2}F_{n+1}F_{n-1}F_{n-2}
\end{align}
と因子分解される. $\quad\Box$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
Fibonacci 数を含む無限連分数
今回の連分数は, 次に示す等式から構成されるものである.
あらゆる整数$m,\ n$にたいして, 等式$F_{m+n+2}=F_{m+2}F_{n+2}-F_mF_n$が成立つ.
帰納法に依る (略).
先述の定理の式
\begin{align}
F_{n+l}F_{n+m}-F_nF_{n+l+m}=(-1)^nF_lF_m
\end{align}
に$n=2$を代入しても得られる. $\quad\Box$
今の命題の式に$m=i+1,\ n=i$を代入し, 両辺を$F_{i+3}F_i$によって割れば
\begin{align}
&F_{2i+3}=F_{i+3}F_{i+2}-F_{i+1}F_i,\\
&\ \\
&\frac{\,F_{2i+3}\,}{\,F_{i+3}F_i\,}=\frac{\,F_{i+2}\,}{\,F_i\,}-\frac{\,F_{i+1}\,}{\,F_{i+3}\,}
\end{align}
を得られる. ここにおいて$a_i=F_{2i+3}/(F_{i+3}F_i),\ $$b_i=F_{i+2}/F_i$と改める. 然らば
\begin{align}
b_i=a_i+\frac{\,1\,}{\,b_{i+1}\,}
\end{align}
が成立ち, 従って
\begin{align}
2=b_1&=a_1+\cfrac{\,1\,}{\,a_2+\cfrac{\,1\,}{\,a_3+\cfrac{\,1\,}{\,\ddots\,}\,}\,}\\
&=\frac{\,F_5\,}{\,F_4F_1\,}+\cfrac{\,1\,}{\,\cfrac{\,F_7\,}{\,F_5F_2\,}+\cfrac{\,1\,}{\,\cfrac{\,F_9\,}{\,F_6F_3\,}+\cfrac{\,1\,}{\,\ddots\,}\,}\,}\\
&=\frac{\,F_5\,}{\,F_4F_1\,}+\cfrac{\,F_5F_2\,}{\,F_7+\cfrac{\,F_6F_5F_3F_2\,}{\,F_9+\cfrac{\,F_7F_6F_4F_3\,}{\,\ddots\,}\,}\,}.
\end{align}
である. 両辺に$F_4F_1$を乗じて整えれば
\begin{align}
1&=\cfrac{\,F_5F_4F_2F_1\,}{\,F_7+\cfrac{\,F_6F_5F_3F_2\,}{\,F_9+\cfrac{\,F_7F_6F_4F_3\,}{\,\ddots\,}\,}\,}\\
&=\cfrac{\,F_3^4-1\,}{\,F_7+\cfrac{\,F_4^4-1\,}{\,F_9+\cfrac{\,F_5^4-1\,}{\,\ddots\,}\,}\,}\\
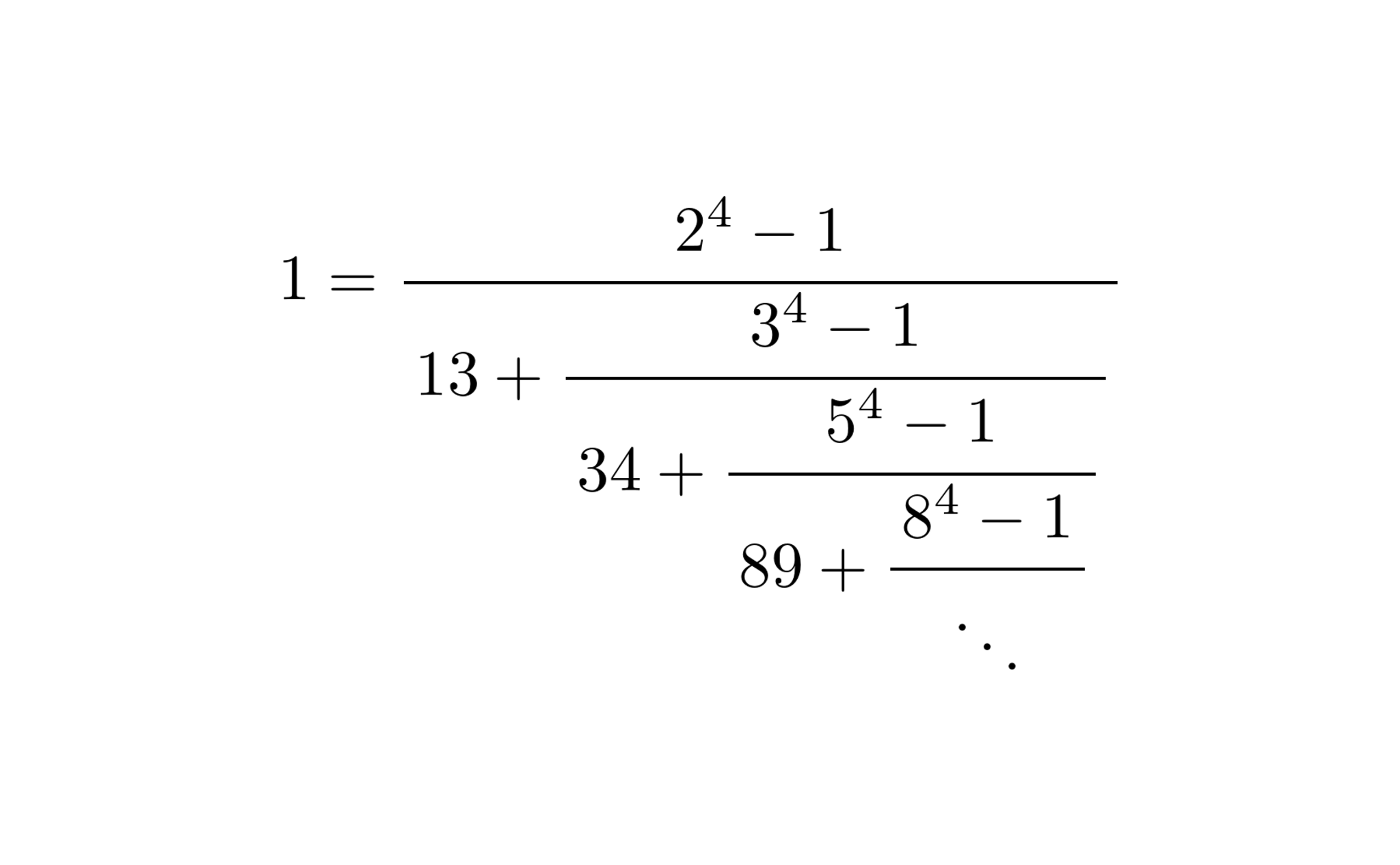
&=\cfrac{\,2^4-1\,}{\,13+\cfrac{\,3^4-1\,}{\,34+\cfrac{\,5^4-1\,}{\,89+\cfrac{\,8^4-1\,}{\,\ddots\,}\,}\,}\,}
\end{align}
となる. 実際, 途中において得られる各$1$の表示分数は, 収束子との誤差が$0$に漸近してゆくように出来ている. 故に収束性も確かである.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
この記事を高評価した人
この記事に送られたバッジ
投稿者
