日曜数学会発表資料「1=0.999...って本当？」

超実数,日曜数学会

766

はじめに

　この記事では私、子葉が1/22(土)に開催された第23回日曜数学会にて発表した内容をそれとなーくまとめたものになります(発表の一部始終についてはここで見れます)。

$1=0.999\ldots$って本当？

スライド1

　こんにちは。子葉です。今日は「$1=0.999\ldots$って本当？」という話をしていきたいと思います。ちなみに左の人物は後で紹介する超実数というものの基礎を築いた数学者であるアブラハム・ロビンソンさんです。

スライド2

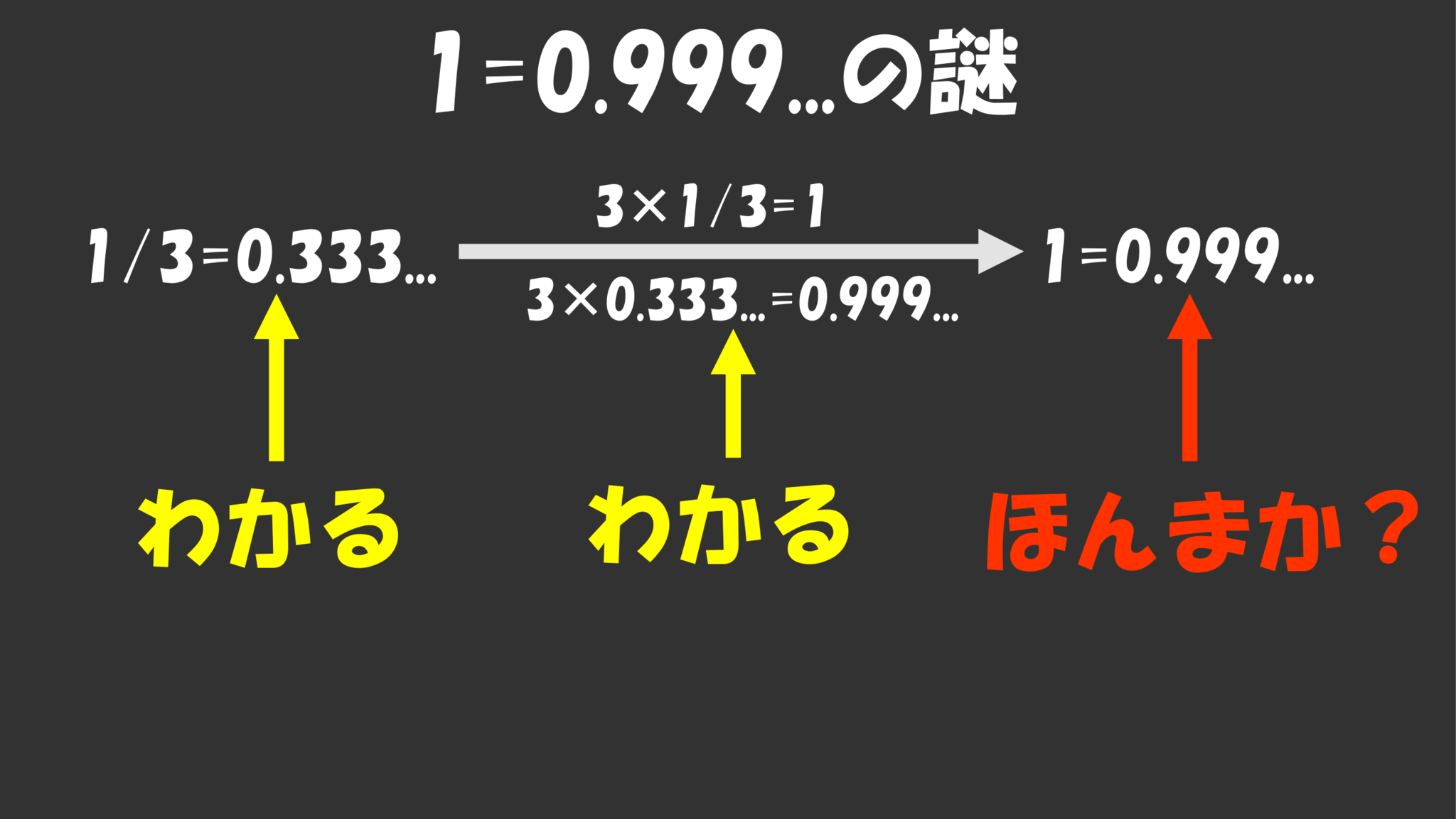
　一か月くらい前に次のような話がTwitterで話題になりました。

・$\dis\frac13=0.333\ldots$
　これはわかります。$1$割る$3$の筆算をすると$0.3$掛けて$1$余って、また$3$掛けて$1$余って、と無限に続くわけですから商は$0.333\ldots$になります。
・$\dis3\times\frac13=1,\quad3\times0.333\ldots=0.999\ldots$
　これもわかります。逆数にもとの数を掛けているから$1$、各桁に$3$を掛けたら$0.999\ldots$ですね。
・以上より$1=0.999\ldots$
　ふむ？う～ん？ほんまか～？同じ$10$進法で違う見た目なのに等しくなんのか～？

　たしかに$1$と$0.999\ldots$は違う数に見えます。これは本当に正しいのでしょうか。

スライド3

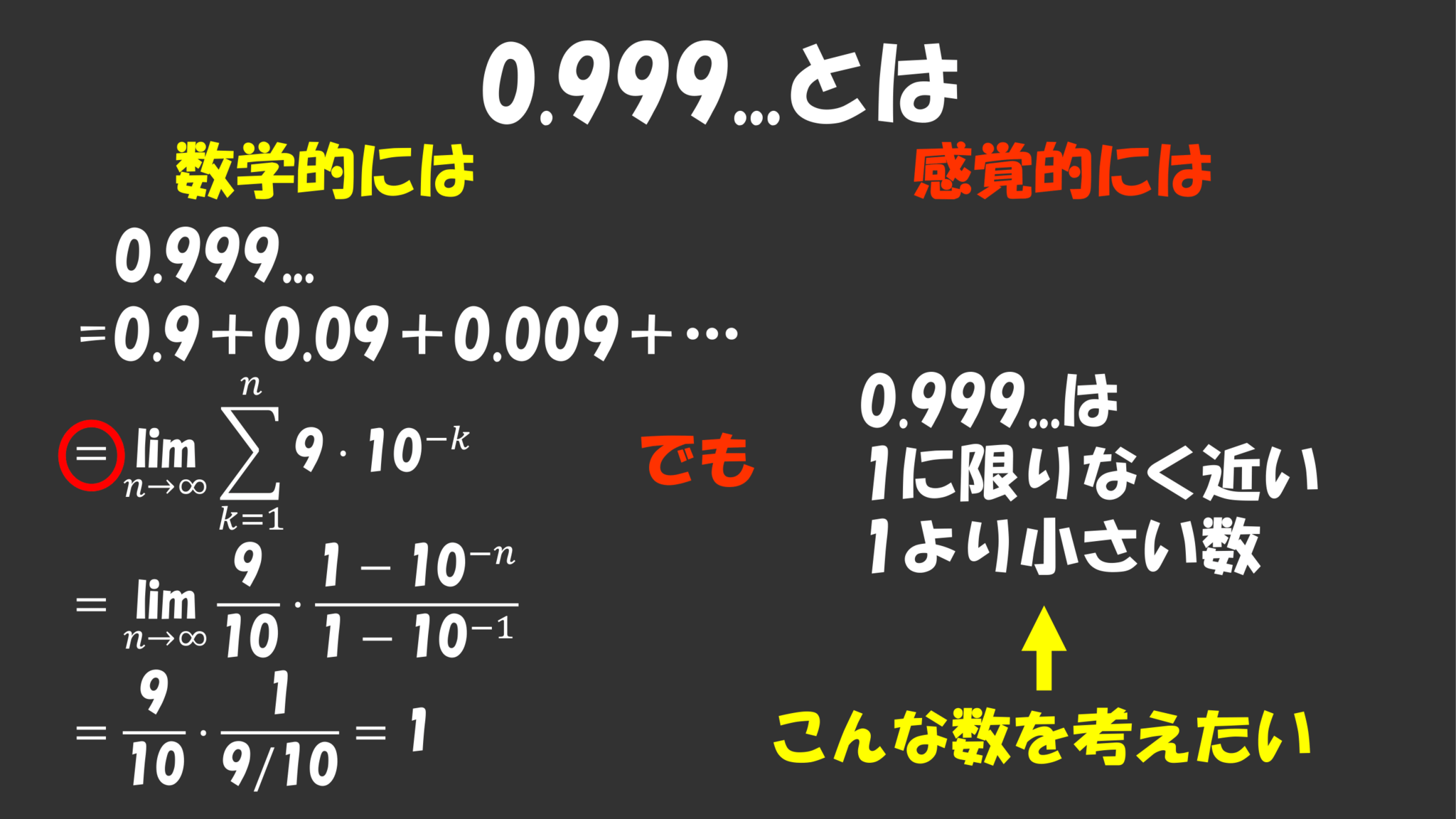
　そもそも$0.999\ldots$って何なのか。というと、まず$10$進法は各桁に$10$の整数乗を対応させた記数法なので
$0.999\ldots=0.9+0.09+0.009+\cdots$
なわけですね。これをちゃんとした数式で書くと
$\dis\lim_{n\to\infty}\sum^n_{k=1}9\cdot10^{-k}$
となります。これは簡単に計算できて、確かに$1$になることがわかります。

でもでもですよ

　やっぱり$0.999\ldots$は「$1$に限りなく近い、けど、$1$よりも僅かに小さい数」であってほしいんです。そんな数を考えたいんです。
　じゃあ考えちゃいましょうよ。
　「といってもさっき$0.999\ldots=1$は証明されちゃったじゃないか。」って？実は先ほど結んだ等号
$\dis0.9+0.09+0.009+\cdots=\lim_{n\to\infty}\sum^n_{k=1}9\cdot10^{-k}$
にはある穴があるんです。ここでは何の断りもなしに「無限に足し合わせる」という操作を「極限」として解釈していました。しかし数学において「無限」の扱いには重々注意しなければなりません。つまり$0.999\ldots$の「極限」以外の解釈の余地があることを忘れてはいけないということです。

スライド4

　じゃあ$0.999\ldots$って結局何なのかというと、すこし飲み込みづらいかもしれませんが、
「数列$(0.9,\;0.99,\;0.999,\;\ldots)$に対応する数」
のことを$0.999\ldots$と考えることにしましょう。
　実数の立場ではこの数列の要素はそれぞれ$1$に対して数値的にほとんど同じ($1\fallingdotseq0.999\ldots9$)なので、対応する数である$0.999\ldots$は$1$に等しい。と解釈していたわけです。この解釈の仕方を「極限」と呼んでいました。

　$0.999\ldots$が$1$と異なる数であるためにはこの解釈を変えなければいけません。そこで「超積」という解釈を用いた超実数というものを考えてみましょう。
　超実数の立場では数列$(1,1,1,\ldots)$と数列$(0.9,\;0.99,\;0.999,\;\ldots)$を比較すると、これらは要素的にほとんど(というか全く)異なる($1\neq0.999\ldots9$)ので、それぞれの数列に対応する数である$1$と$0.999\ldots$は異なる数である。といった解釈をします。
　かくして$1\neq0.999\ldots$である。という主張に正当性を持たせることができました！やったね！
　
　おいおいおい。ちょっと待てと。
　いきなり超実数とかいうよくわからない数が出てきたけどもよ、でたらめなことを言われちゃ困る。でたらめな世界で$1\neq0.999\ldots$が成り立ってもちっとも嬉しかねえ。俺たちゃあくまで"感覚的な数"として$0.999\ldots$は「$1$に限りなく近いけど、$1$よりも僅かに小さい数」であってほしいんだわ。と。
　そう思われるかもしれません。では超実数がいかに"感覚的な数"であるか説明しておきましょう。

スライド5

　超実数とはどんな数であるか、簡単な特徴をまとめると次のようになります。ちなみに一番上の項は超実数の定義となりますが、ややこしいので省略します(この"ほとんど同じ"と表現した関係が意外とクセモノで、実は超実数は"ほとんど同じ"の意味の定め方によって違う数が出来たりします。詳しくは参考文献を参照してください)。
　まずこの「$1=0.999\ldots$問題」においてもっとも注目したい性質としてほとんど実数と同じ構造を持つという点が挙げられます。超実数は数列によって特徴づけられる数なので項ごとに演算や関係を考えることで四則演算や不等式、また実関数への超実数の代入などが考えられ、それらは実数と全く同じ感覚で扱うことができます(例えば四則演算には体、不等式には全順序という構造が入っています)。
　また超実数ならではの性質として無限小や無限大が"数"として存在しています。

※ここは少し長くて小難しいので読み飛ばしてもらってかまいません
　ここで注意してほしいのが無限小とは「(絶対値が)どんな正の実数よりも小さい超実数」であって「どんな正の"超"実数よりも小さい超実数」ではありません。超実数には無限小と呼ばれる数が無数に存在しており、(全順序なので)それぞれに大小関係が考えられます。全ての($0$でない)無限小にはそれよりも$0$に近い無限小が存在するんですね(例えば無限小$\e\;(\neq0)$に対して$\frac12\e$は$\e$よりも$0$に近い無限小になります)。無限大についても同様です。
　無限小$\e$や無限大$\infty$という概念は定数のように考えがちですが、超実数の世界においては無限小も無限大も無数に存在し、「$m,n$を自然数とする」とか「$p$を素数とする」と言うのと同じように$\e$や$\infty$も「無数にある無限小・無限大の中から一つ選んで$\e,\infty$とおいた」と考えるのが適切だと思います。こうすることで本来考えることができなかった$\e\cdot\infty$や$\frac{\infty}{\infty}$などを考えたりすることができます(これらの値は$\e$や$\infty$の取り方によって変わります。$\frac\infty\infty$は$1$ですが、分母と分子が違う無限大超実数$\infty_1,\infty_2$ならば一定の値は取りません)。

　そしてこれも今回の話題として注目したい性質として(有限)超実数は実数からちょっと(無限小)だけずらしたものであるという性質があります。具体的には無限大ではない任意の超実数$a$に対してある実数$\a$(と無限小$\e$)が一意に存在して$a=\a+\e$と表せれる。というわけです。これは"個人的な感覚"として「超実数は数直線上には(実数しか)存在しないが数直線上の"点の中"に存在する」とか「超実数は数直線上の各点に厚みを持たせた数である」といった風にイメージしています。

※ここも少し長くて小難しいので読み飛ばしてもらってかまいません
　以上より超実数がいかに"感覚的な数"であるかはなんとなくわかってもらえたと思います。とはいってもまだ超実数は「天下り的に出てきた数」であることには変わりないと思うので最後にこのような数を考えるメリットを簡単に紹介しておきましょう。
　上では「無限小や無限大が数として扱える」そして「超実数は実数をちょっとずらしたもの」という性質があることを紹介しましたが、それらの性質を使えば関数の極限を直感的に扱うことができます。例えば「$\dis\lim_{x\to\infty}f(x)=\a$である」とは超実数の世界において「任意の無限大$\infty$に対して$f(\infty)=\a+\e$が成り立つ」と言い換えられます。もしくは超実数$a$の$a=\a+\e$という表示に対し、この実数部分(これを標準部と言います)を取り出す関数$\st(a)=\a$を使うと「任意の無限大$\infty$に対して$\st(f(\infty))=\a$が成り立つ」と表現することができます。
　特に面白いのが微分との関係で、微分とは接線の傾きを「ちょっとずらした点との傾き」を考えることで求める手法でした。それが超実数の世界では"ちょっとずらす"という操作が"無限小だけずらす"という具体的な表現に代わるので、「グラフ$y=f(x)$の$x=a$における接線の傾きが$m$である」とは「任意の無限小$dx$に対して$\dis\frac{f(a+dx)-f(a)}{dx}=m+\e$が成り立つ」もしくは「任意の無限小$\e$に対して$\dis\st\l(\frac{f(a+dx)-f(a)}{dx}\r)=m$が成り立つ」と表現できます。
　このように書けるのがどのように面白いのかというと、例えば$x^3$の微分を考えてみたとき、任意の無限小$\e$に対し
$\dis\frac{(x+\e)^3-x^3}{\e}=3x^2+3\e x+\e^2$
が成り立ちますが、無限小の持つ「(無限小)×(有限超実数)=(無限小)」「(無限小)+(無限小)=(無限小)」という性質を考えると$3\e x+\e^2$は無限小となります。つまり
$\dis\st\l(\frac{(x+\e)^3-x^3}{\e}\r)=3x^2$
となって$x^3$の導関数が$3x^2$であることがわかります。この「無限小が数として扱える」ことの面白さが伝わったかどうかわかりませんが(実際のところ極限による計算とやってることは同じだし)、まあ少しでも興味を持ってもらえたなら嬉しいです。

スライド6

　なにはともあれこの"実数とよく似た数・実数をちょっと膨らませた数"であり"無限小や無限大が数として扱える"という点で"感覚的な数"である超実数を皆さんが(存在する)数であると認めるならば、$0.999\ldots$は確かに「$1$に限りなく近いけど、$1$よりも僅かに小さい数」であってくれ(るように定義することができ)ます。(ちなみにこの場合そもそも$\frac13\neq0.333\ldots$なので冒頭の$1=0.999\ldots$の導出は最初っから間違っていることになります。)
　そしてあくまで実数だけが数だと考えているのであれば$1$と$0.999\ldots$が違う数に見えるのは、おそらく「任意の実数は$10$進法で"一意的に"表すことができる」という誤った先入観を持っているせいなだけで、ただの気のせいです。
　どちらにせよ$1\neq0.999\ldots$となる世界もあるということは知っていただけるとありがたいです。

スライド7

　ご清聴ありがとうございました。

おまけ

　今回の発表の後に「発表では数列$(0.9,\;0.99,\;0.999,\;\ldots)$に対応する超実数を$0.999\ldots$とおいていたが、他の数列で定義したらどうなるのか」という質問をいただいたのですが、実のところ例えば一項ずらした数列$(0,\;0.9,\;0.99,\;0.999,\;\ldots)$に対応する超実数を${}^*0.999\ldots$とおくと${}^*0.999\ldots\neq0.999\ldots$となります(「$1$に限りなく近いけど、$1$よりも僅かに小さい数」であることには変わりませんが)。同一視の条件が「ほとんどの$n$に対して$a_n=b_n$」というかなり狭い命題であるだけに数列の構成がちょっと違うだけで違う超実数が出来てしまいます。こうなってくると「超実数の$0.999\ldots$って結局何なのか」となってきますね。(強いて言うなら「$1$に限りなく近いけど、$1$よりも僅かに小さい数」全体のことを指すものとでも定めておけばいいと思いますけど。)

　(追記)twitterの方で既に何人かの方から指摘されている通り超実数において「$0.999\ldots$を何と定めるか」ということについてはいくつもの視点があり、そしてその視点によって違う数が出来てしまいます。また超実数の世界においても$0.999\ldots$の解釈の仕方によっては$1=0.999\ldots$が成り立つこともあります。そのことについては私も理解しています。
　ただ今回の発表の趣旨としては$1=0.999\ldots$問題に「$0.999\ldots$は『$1$に限りなく近いけど、$1$よりも僅かに小さい数』であってほしい」「実数の世界では"そういう数"が存在しないから等号が成立してしまう」という背景があることに対して「"そういう数"の存在する世界があって、$0.999\ldots$をそのような数として解釈できる($0.999\ldots$に似ても似つかない数が"そういう数"だったとしても仕方ないですからね)」という別の視点があることを伝えるのが主であり、「$0.999\ldots$が何者であるか」という話題については意図的に避けるようにしています。その点については理解していただけるとありがたいです。

　また今回紹介した「$1=0.999\ldots$問題」には「$1\neq0.999\ldots$じゃないの？」という立場と「いやいや$1=0.999\ldots$でしょ」という立場の人がいますが、私としては発表者の皆さんに言われたように「$1=0.999\ldots$であることに納得いかない人たちに『君たちの考えが完全に間違っているわけじゃないよ』と手を差し伸べる発表」というよりも「$1=0.999\ldots$に決まってんじゃんと思っている人たちに『決め付けるのはよくないよ』と指摘する発表」のつもりで発表をしていました。個人的に数学の面白さとして「自分のやりたいことを定式化すること」よりも「今までの常識・固定観念を破壊すること」の方が好きなので、みなさんにもそういった面白さを伝えたかったわけです。
　まあなんにせよ超実数とは中々面白い概念なので私の発表を機にみなさんに興味を持ってもらえたのなら嬉しい限りです。超実数についてもっとよく知りたいという人は、手始めに今回私が参考にさせていただいた文献を読んでみると入門として丁度いいかもしれません。

　とりあえず今回はこんなところで。では。　