有向角の使い方
「数学オリンピック幾何への挑戦：ユークリッド幾何学をめぐる船旅」に有向角の解説が載っています. 参照してください.
はじめに
この記事では、数学オリンピックでよく使われる有向角という表記方法を紹介します。有向角は問題を解く際のテクニックではなく、答案を簡潔に書く方法です。有向角は答案を綺麗に書くのに非常に便利な記法ですが、インターネット上に出回っている情報が少ないと思い、この記事を作成しました。初心者にもわかりやすい丁寧な説明を心掛けましたが、もしも不鮮明な箇所・誤植等ございましたら遠慮なくコメントにてご指摘ください。
この記事にかかわらず、今後私の全ての記事において、「共点」で3本以上の図形が1点で交わること、「共線」で3点以上が同一直線上にあること、「共円」で4点以上が同一円周上にあることを指します。
有向角導入の前に
証明の欠陥を探せ
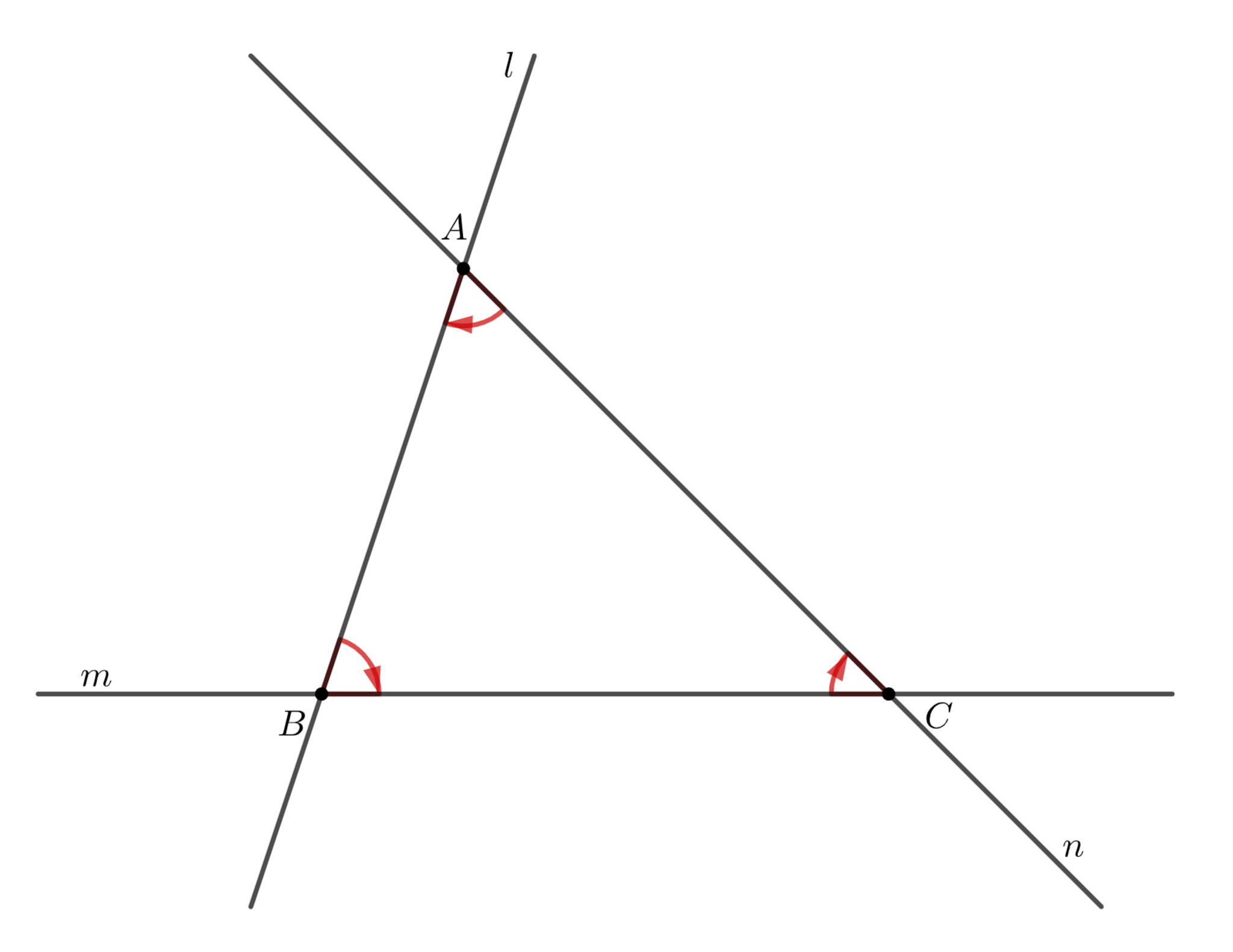
早速ですが、以下のミケルの三角形定理の証明には重大な欠陥が含まれています。それはどこでしょうか。
ミケル (Miquel) の三角形定理:
三角形$ABC$がある. 直線$BC,CA,AB$上にそれぞれ点$D,E,F$をとるとき, 円$AEF,BDE,CDF$は1点$P$で交わる. この$P$をミケル点 (Miquel Point)という.
円$AEF,BDE$の交点を$P$とする. 4点$CPDF$の共円を示せばよい.
円$APEF$について, $\angle CDP=\angle BEP$
円$BPDE$について, $\angle BEP=\angle PFA$
よって, $\angle CDP=\angle PFA$
従って, 4点$CPDF$は共円であるから主張は従う.
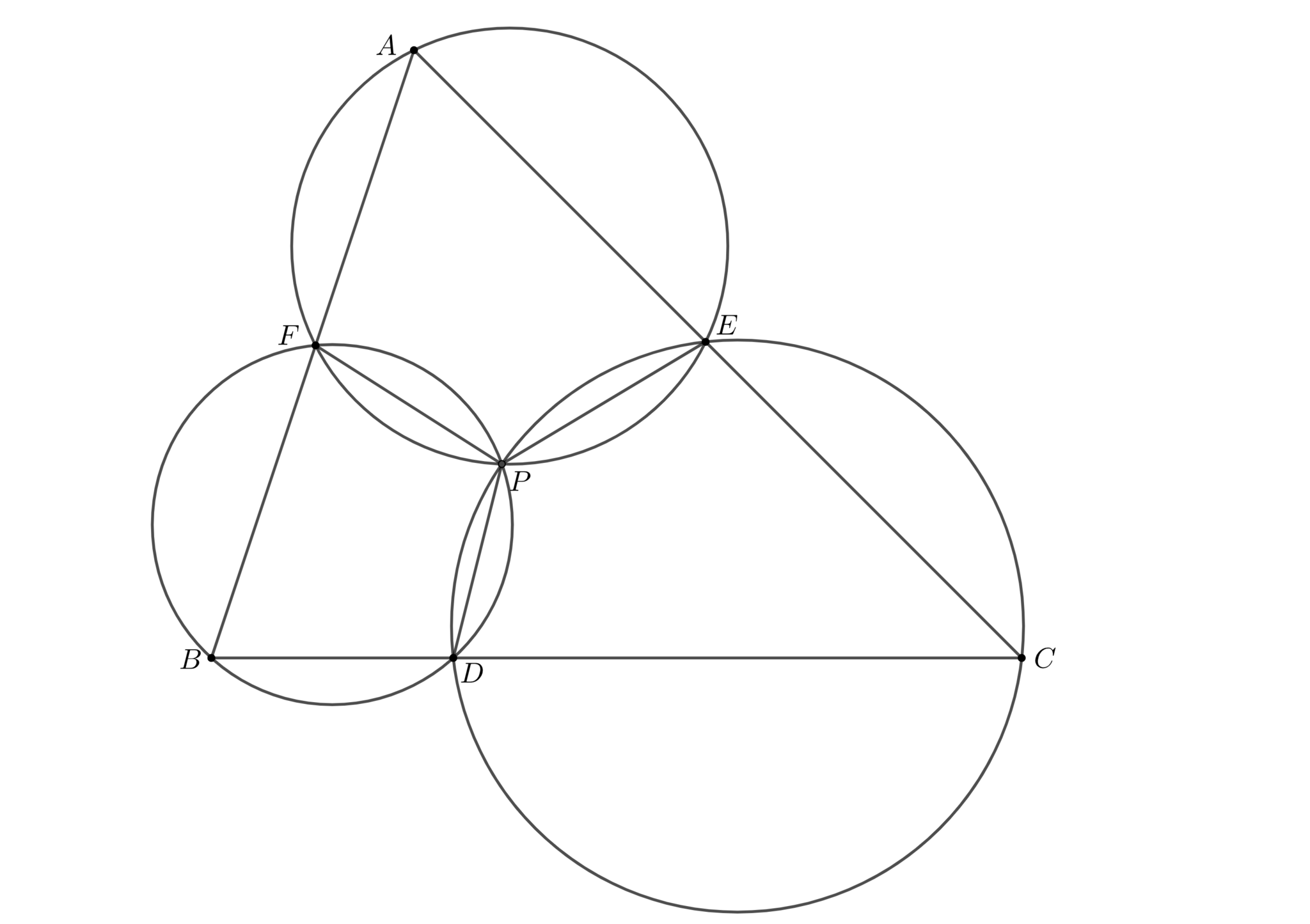ミケルの定理
幾何でよくある間違い
まずは条件不足などの理由で偽である命題を2つみていきましょう。
偽命題:
平面上にどの3点も共線でない4点$A,B,P,Q$がある. このとき, $\angle APB=\angle AQB$ならば4点$ABPQ$は共円である.
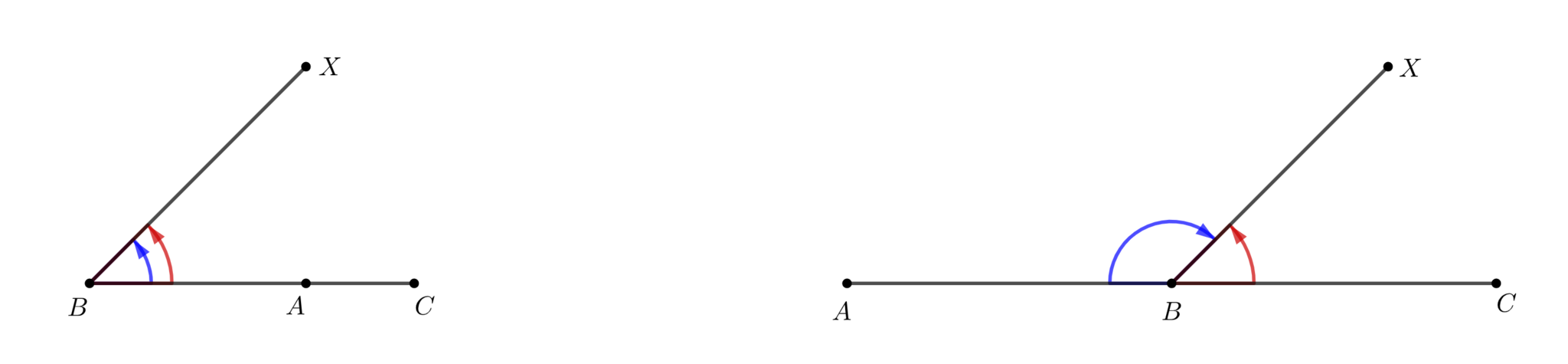
よく学校で円周角の定理を習うときに注意されることですが、命題2では$P,Q$が$AB$について同じ側にあるときという条件が抜け落ちています。図2のような状況ではこの命題は成り立ちますが、図3の様に$P,Q$が$AB$に対して反対側にあると成り立たなくなってしまいます。
答案中に円周角の定理の逆を用いる際には位置関係に注意するようにしましょう。
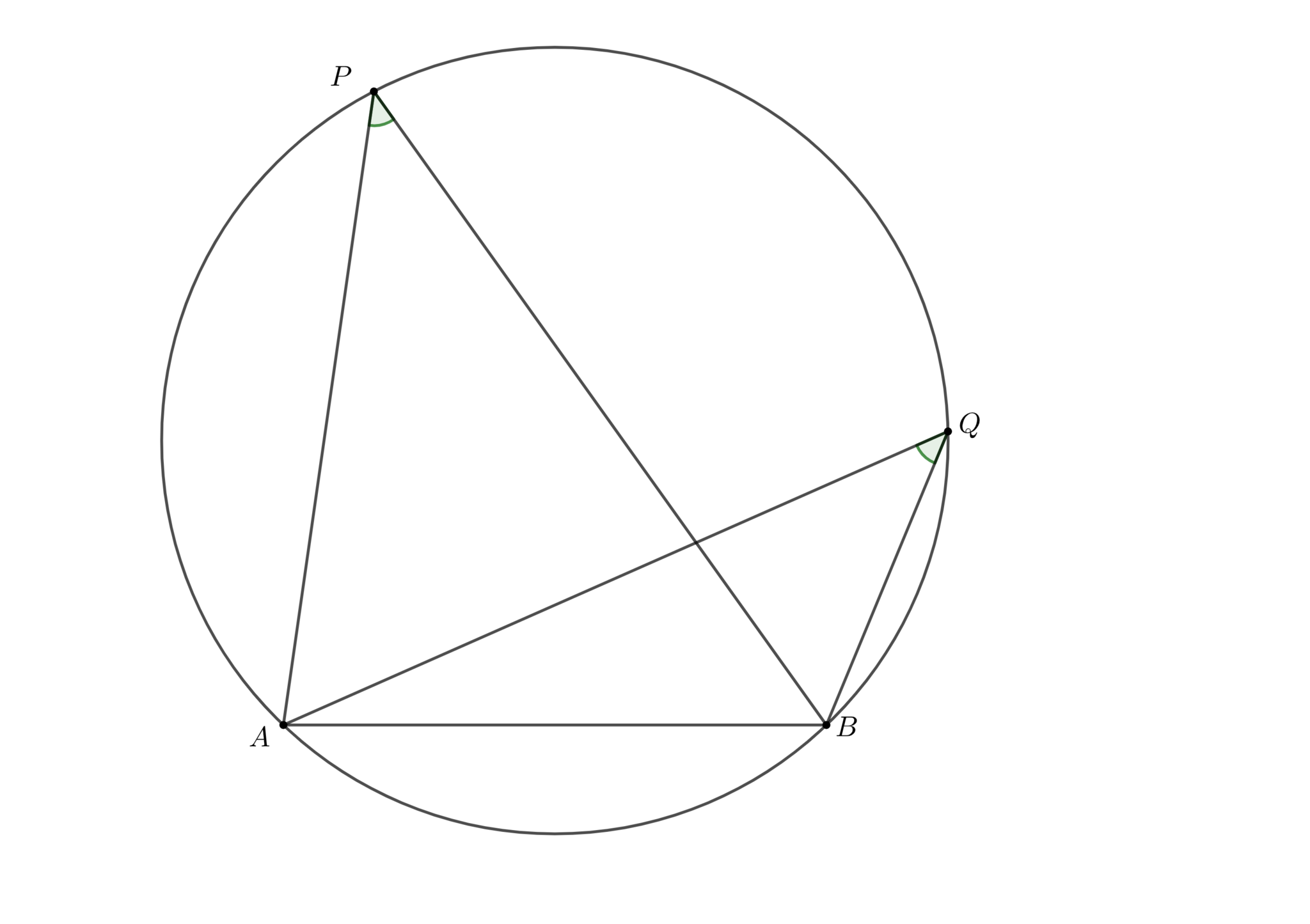同じ側
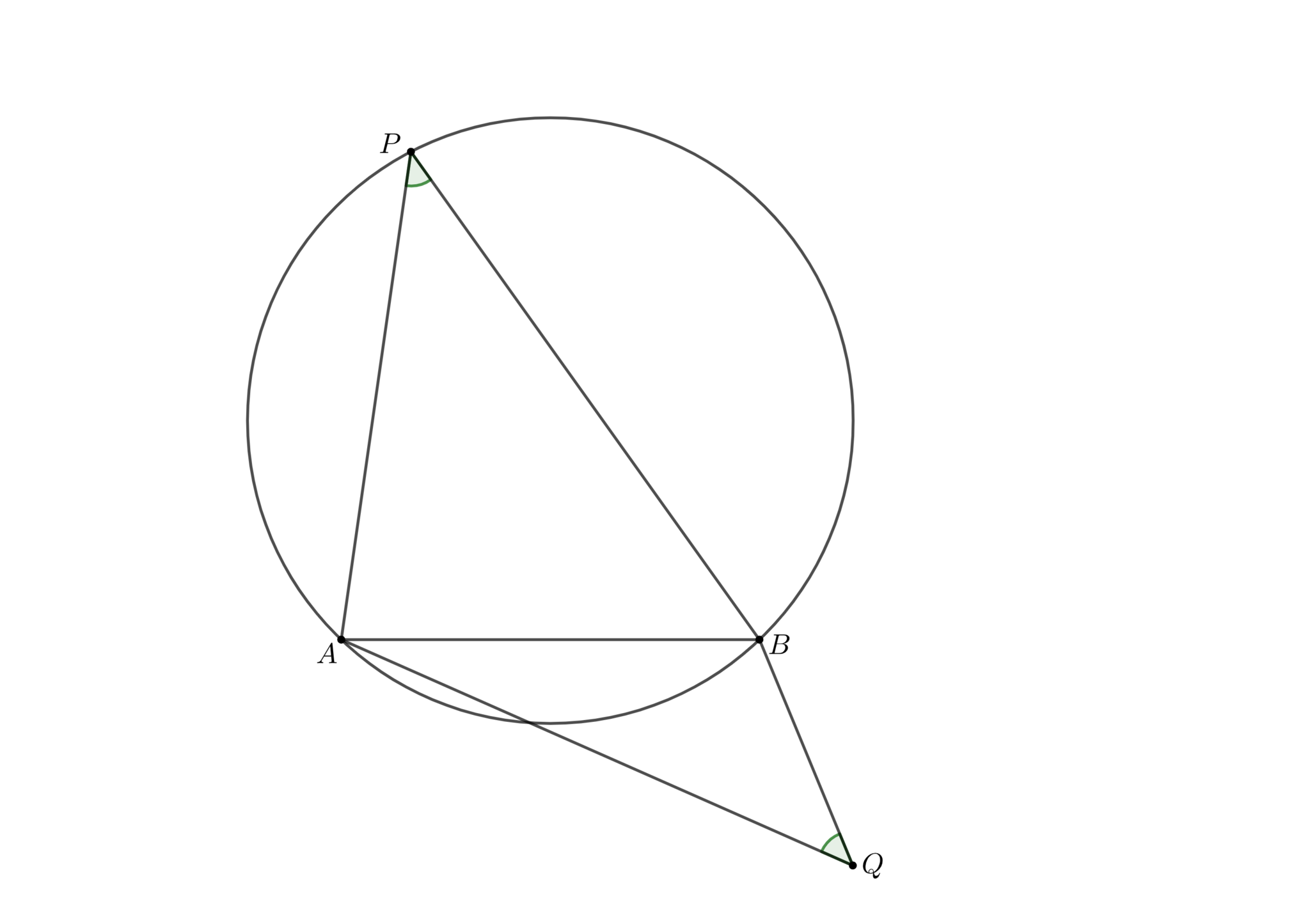異なる側
偽命題:
平面上にどの3点も共線でない4点$A,B,O,P$について, $\angle AOP+\angle POB=\angle AOP$が成立する.
これは「角度の足し算」といえます。$P$という中継地点を経由して角度を測るときそのまま足すことはできません。この場合は$A,B$が$OP$について異なる側にあるという条件が抜けています。図4のような状況ではこの命題は成り立ちますが、図5の様に$P$が$\angle AOB$の「外」にあるときは明らかに右辺の方が大きくなります。
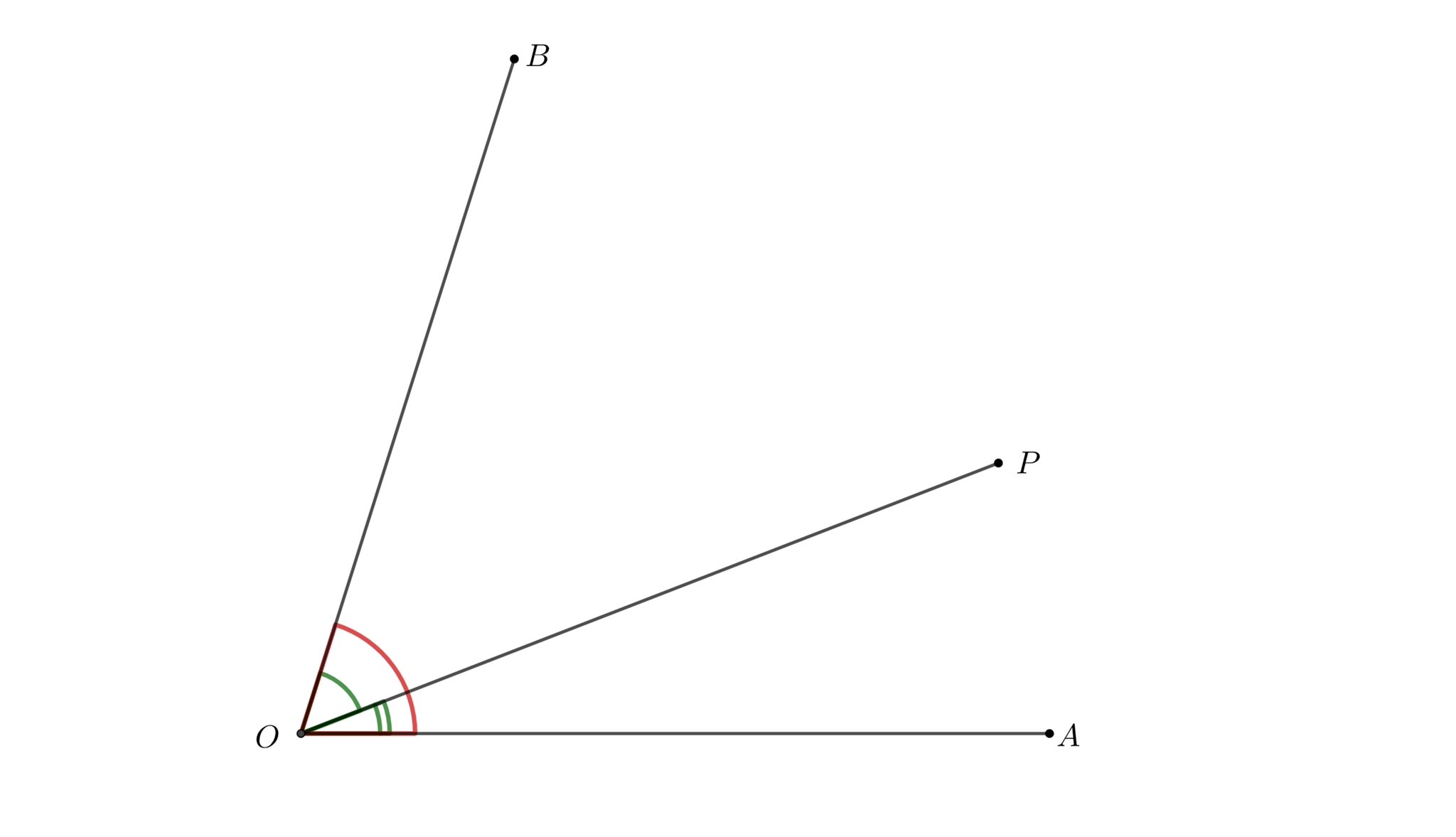Pが角の「内部」
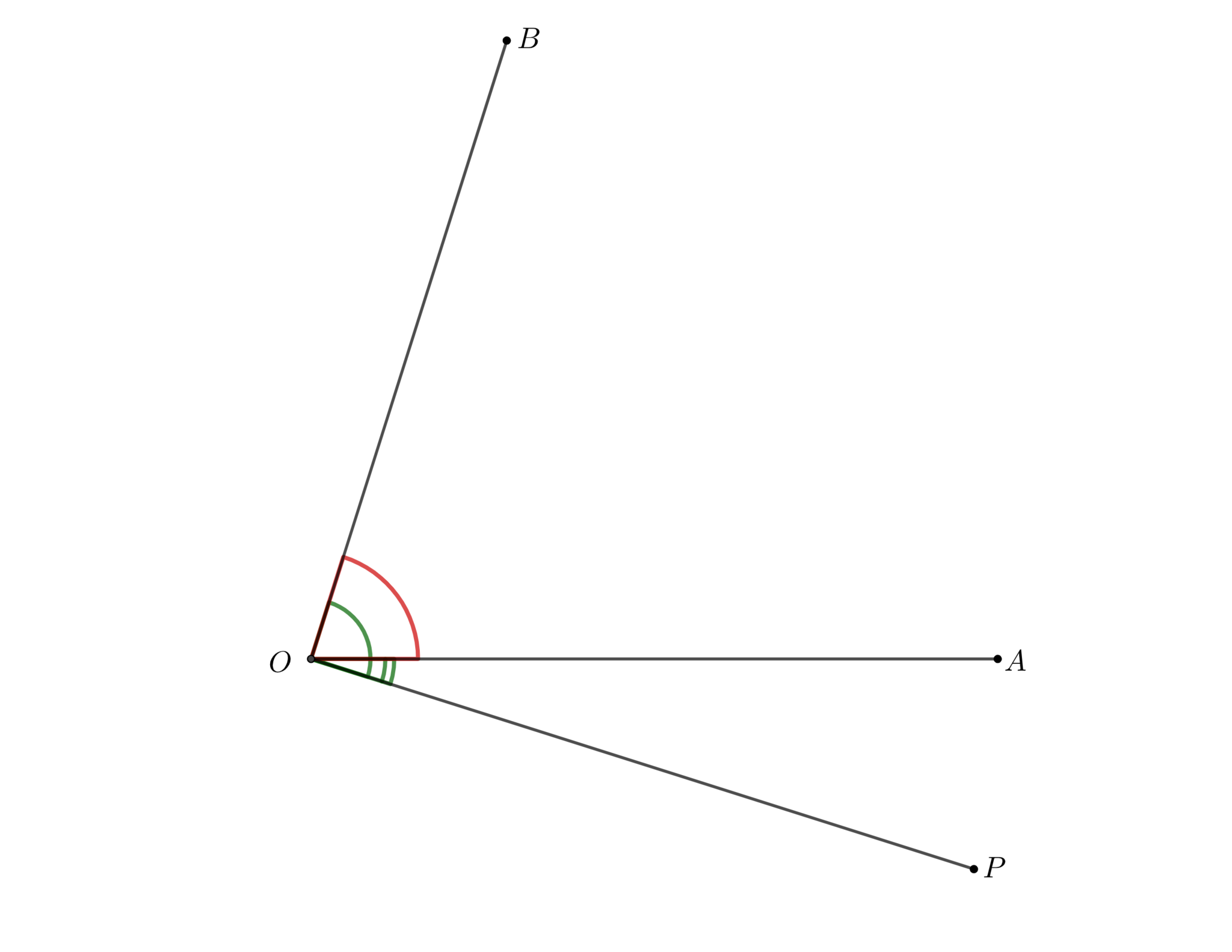Pが角の「外部」
図の位置関係に依らない議論をするということ
2つの偽命題に共通しているのは、図の位置関係による場合分けが不足しているという点です。数学オリンピックの幾何では、図の位置関係に依らない議論をすることがとても重要であり、本選以降の記述式問題においてはコーナーケース（ある点とある点が一致して証明が破綻してしまう場合）は分離して記述しないと減点されることがあります。
しかし、円周角の定理が出てくるたびに位置関係を確認するのは少し面倒です。そこで有向角を導入すると、これらの問題を解決することができるのです。
有向角の定義
有向角の特徴は、符号付き角度、つまり負の角度を導入するという点です。座標やベクトルといった解析幾何が誕生する以前のユークリッド幾何学では、負の角度の概念はまだ存在しませんでした。しかし、解析幾何のような抽象的な手法が用いられるようになると、厳密性を求め、負の角度の概念を考えるようになりました。
平面上に2直線$l,m$がある. $l$を反時計回りに$\theta$回転させると$m$に重なるとき, $\theta=\measuredangle (l,m)$とする.
逆向きに測ると正負が反転 : $\mang (l,m)=-\mang (m,l)$
有向角は、反時計回りに測る際は正の値、時計回りに測るときは負の値になります。
有向角の記号の$\TeX$コマンドは\measuredangleです。
図6において$\measuredangle (l,m)=50^{\circ},\measuredangle (m,l)=130^{\circ}$である.
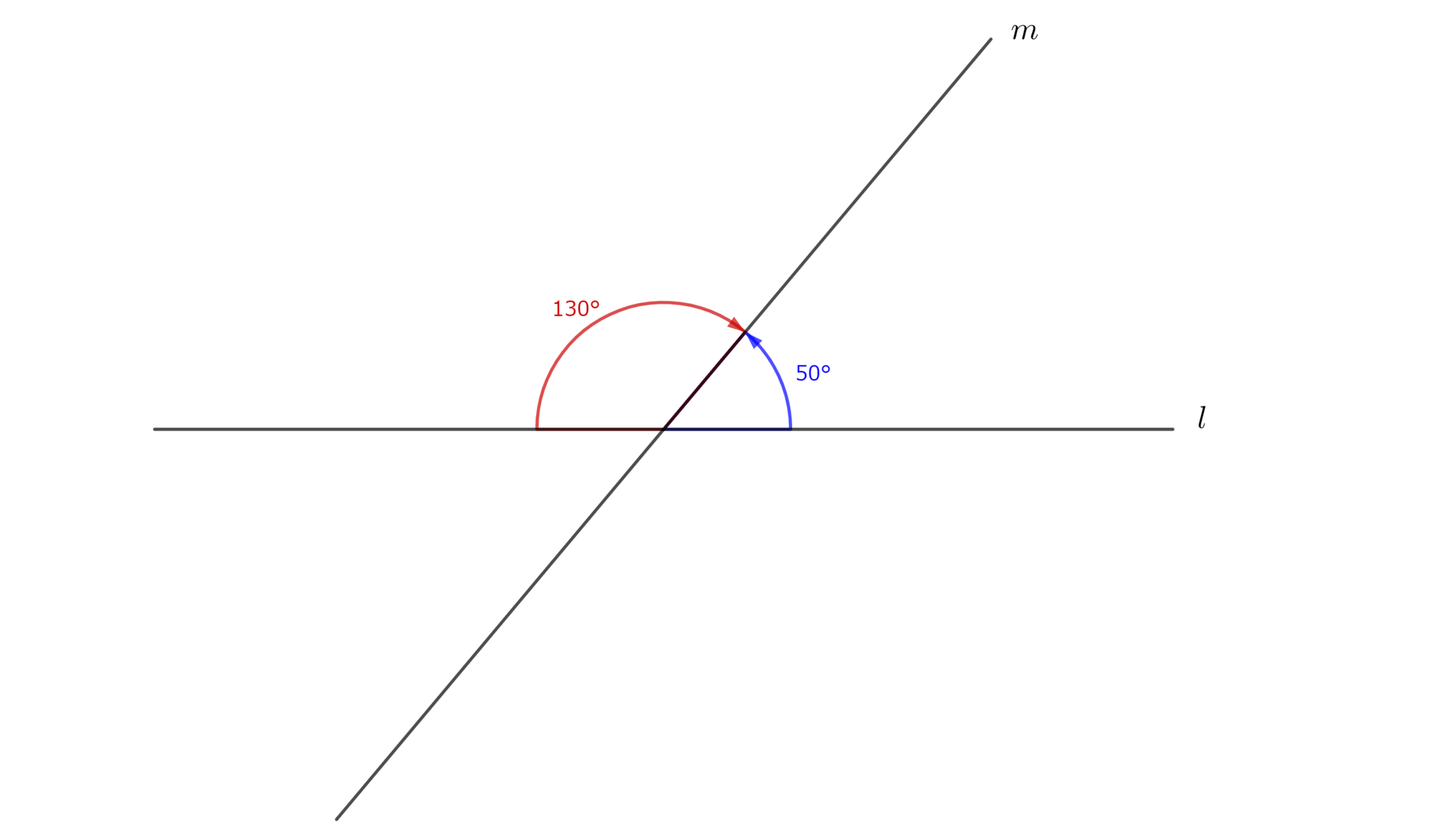例1
有向角において, $180^{\circ}$を法として合同な角度は同一視する. 例えば, 例1において$\mang (l,m)=50\do=230\do=410\do=-130\do=-310\do=\cdots$である.
なお, 便宜上$\mathrm{mod}180\do$における$\equiv$を省略し, 単に$=$とかく.
負の角度の定義はできましたが、2直線$l,m$に対しての定義では普段我々が使っている通常の角度$\angle ABC$と表記の形式が異なるため、3点$A,O,B$に対して有向角を定義します。
平面上の3点$A,O,B$に対し, $\mang AOB=\mang (AO,BO)$と定める.
逆向きに測ると正負が反転 : $\mang AOB=-\mang BOA$
図7において$\measuredangle AOB=50^{\circ},\measuredangle BOA=130^{\circ}$である.
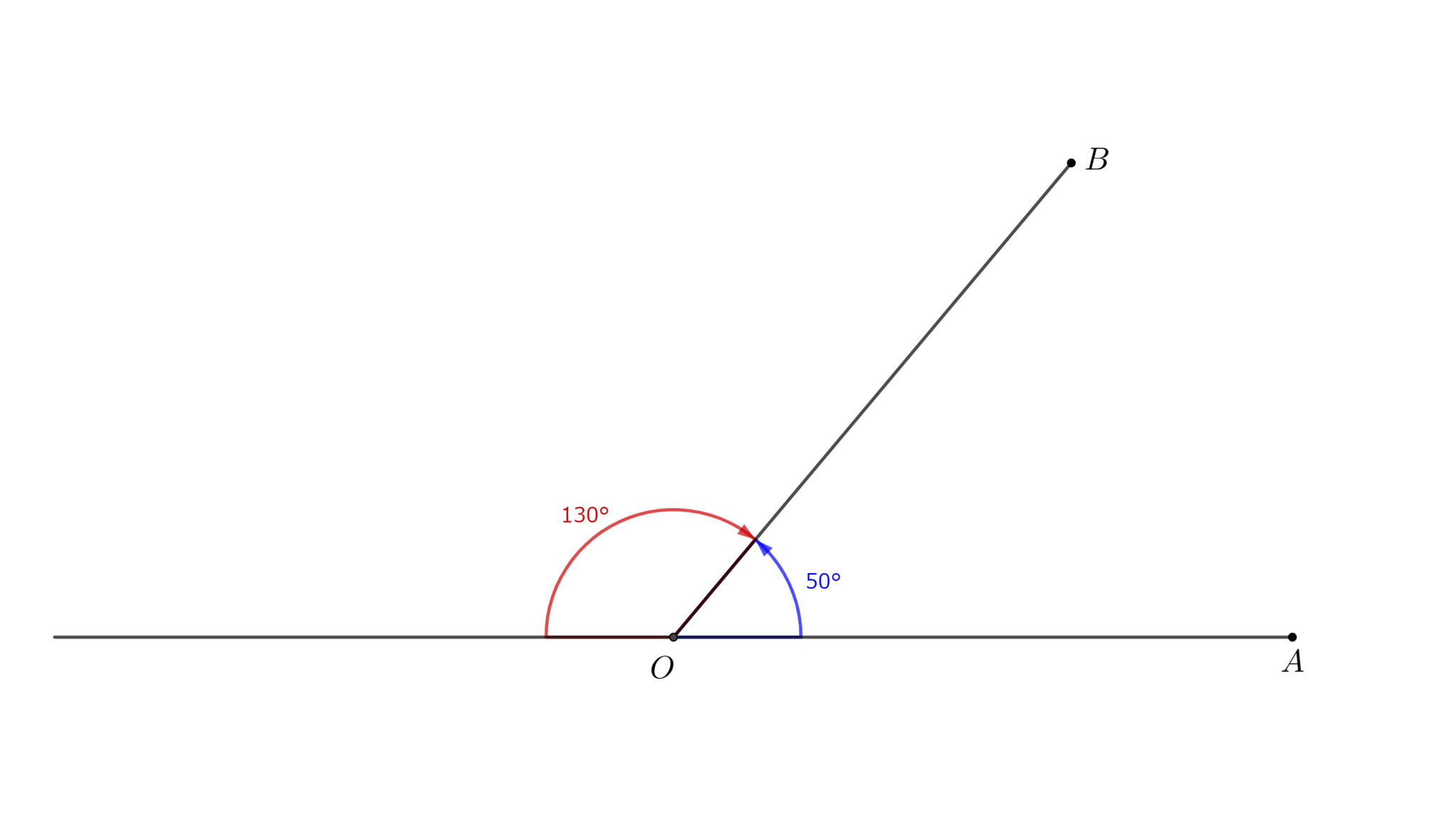例2
$\mang (l,m)$の記法は交点に名前の付いていない2直線がなす角を測るときによく使われます。どちらの表記方法にも慣れておきましょう。
有向角の性質
有向角の加法
幾何でよくある間違いの所で紹介した角度の足し算ですが、有向角を用いると通常の角度では偽であった命題を問題なく使えるようになります。
3直線$l,m,n$について, $\mang (l,m)+\mang (m,n)=\mang(l,n)$
4点$A,O,B,P$に対し, $\mang AOP+\mang POB=\mang AOB$
明らか. わからない場合は図を見て理解せよ.
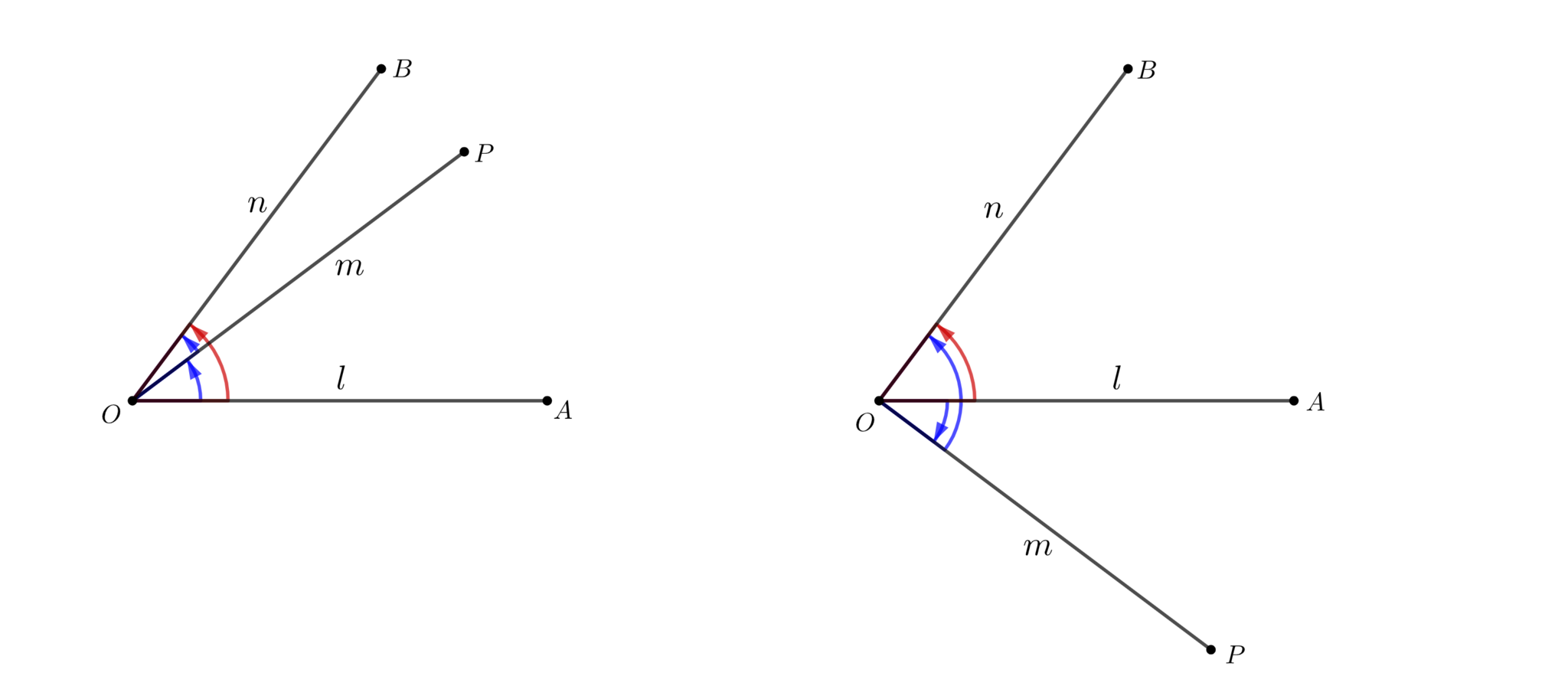定理4
共線条件
有向角を用いると、共線を簡単に判定することができます。
4点$A,B,C,X$に対し, 3点$A,B,C$が共線である必要十分条件は$\mang ABX=\mang CBX$である.
$A,B,C$が共線
$ \Longleftrightarrow $ $\mang ABC=0$
$ \Longleftrightarrow $ $\mang ABX =\mang ABC+\mang CBX=\mang CBX$（命題1より）
よりよい.
定理5
共円条件
通常の角度では共円条件は2つに場合分けをする必要がありました。有向角を用いると、この2つの場合分けを1つにまとめることができます。その前に通常の角度における共円条件を確認しておきましょう。
平面上のどの3点も共線でない4点$A,B,P,Q$に対し, 次が成り立つ.
$P,Q$が$AB$について同じ側にあるとき:
4点$ABPQ$が共円$ \Longleftrightarrow $ $\angle APB=\angle AQB$
$P,Q$が$AB$について異なる側にあるとき:
4点$ABPQ$が共円$ \Longleftrightarrow $ $\angle APB+\angle AQB=180\do$
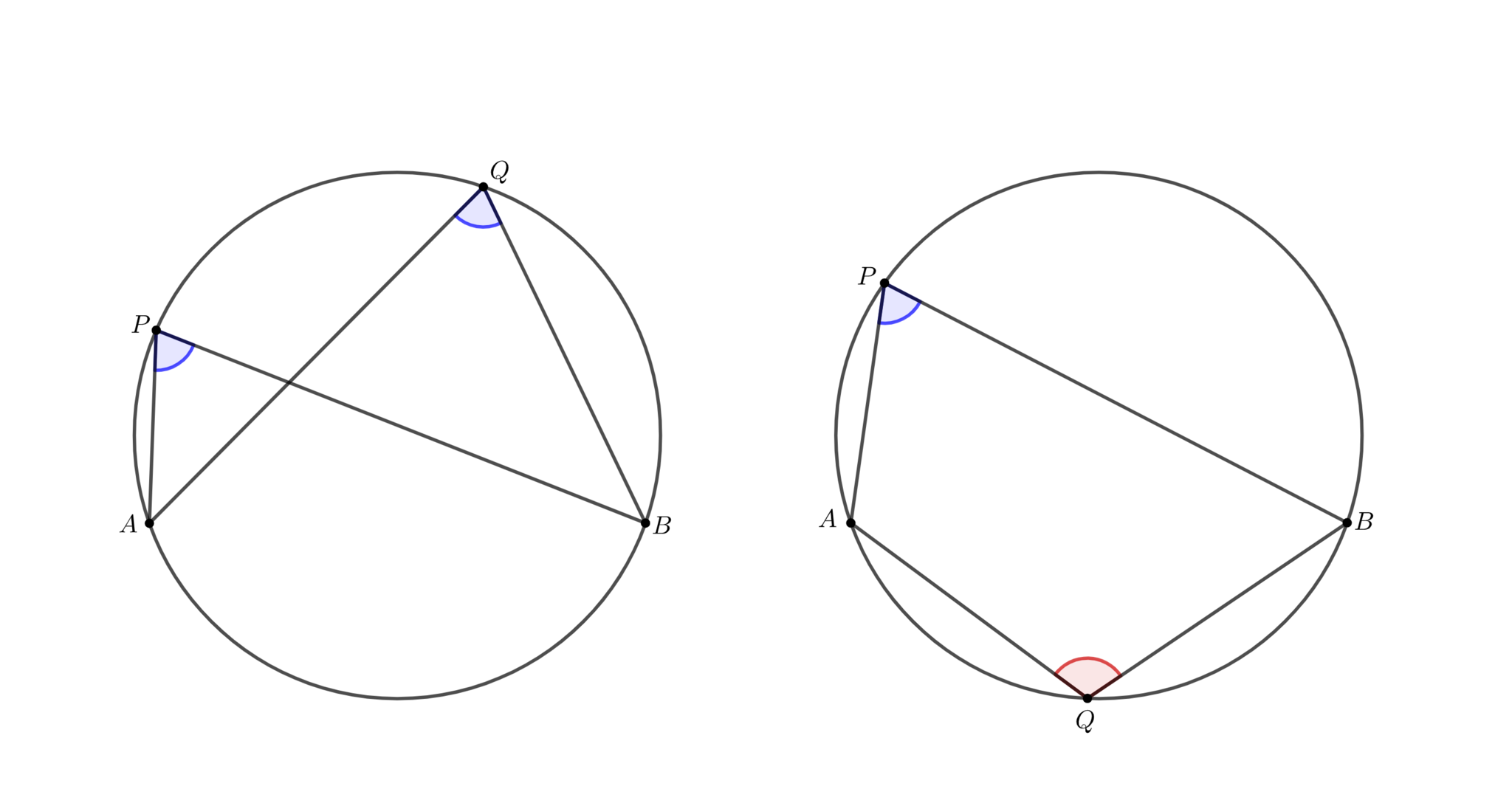定理6
平面上にどの3点も共線でない4点$A,B,P,Q$に対し,次が成り立つ.
4点$ABPQ$が共円$ \Longleftrightarrow $ $\mang APB=\mang AQB$
通常の角度と有向角を等号で結ぶ際のみ区別のため$\equiv$を用いる.
$P,Q$が$AB$について同じ側にあるとき:
明らか.
$P,Q$が$AB$について異なる側にあるとき:
($\Rightarrow$)を示す.
$\mang APB>0$として一般性を失わない
$$
\begin{eqnarray*}
\mang APB &\equiv& \angle APB （\mang APB>0\text{より}）\\
&=& 180\do-\angle AQB （命題3より）\\
&\equiv & -\mang BQA\\
&=& \mang AQB （\text{定義1系より}）
\end{eqnarray*}
$$
逆は容易であるため読者への課題とする.
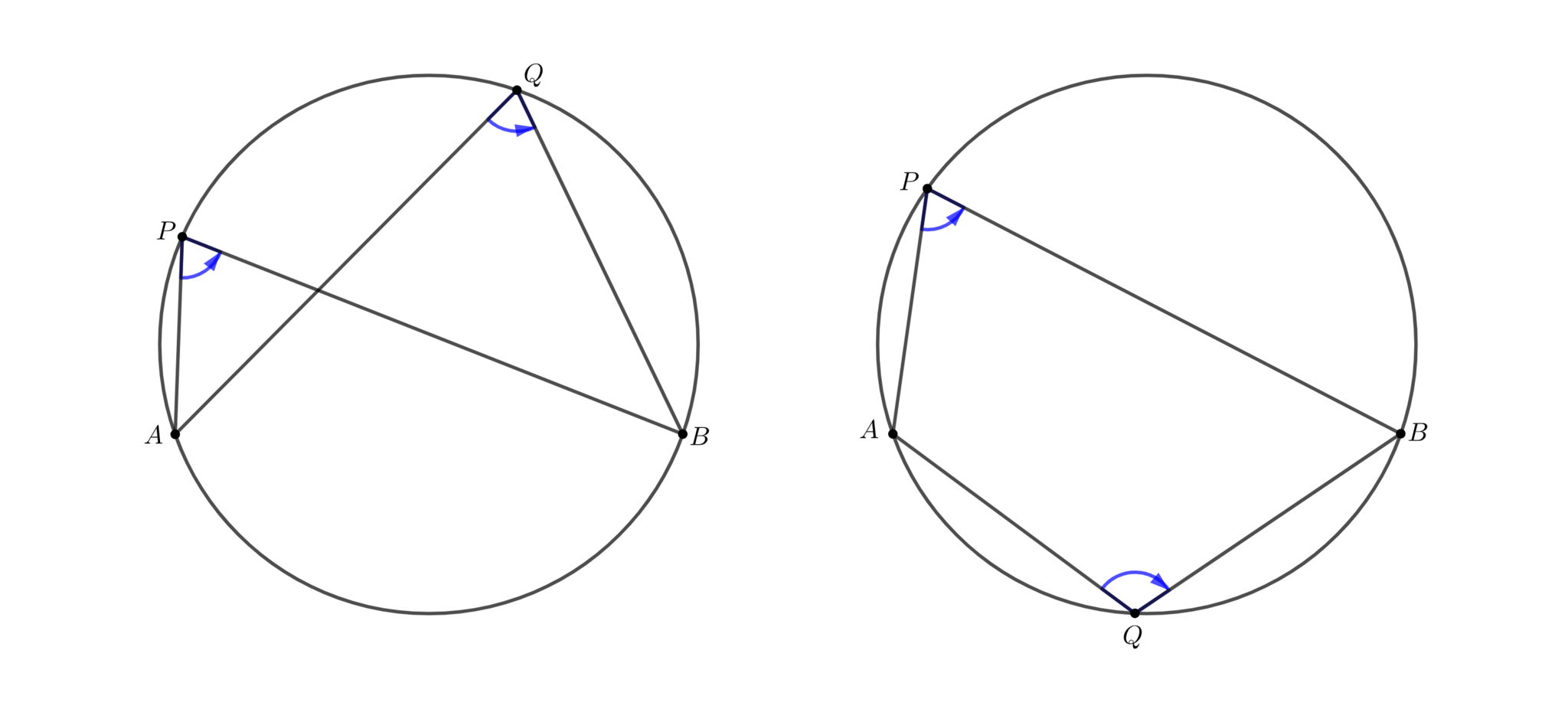定理7
三角形の内角の和
通常の角度において三角形の内角の和が$180\do$になったことと似たことが有向角においても成り立ち、さらにそれは3直線に一般化されます。
3直線$l,m,n$に対し, $\mang (l,m)+\mang(m,n)+\mang(n,l)=0$
特に, 3点$A,B,C$に対し, $\mang ABC+\mang BCA+\mang CAB=0$
明らか.
定理8
二等辺三角形
3点$A,B,C$に対し, $AB=AC \Longleftrightarrow \mang ACB=\mang CBA$
中心角の定理
共円条件だけでなく中心角の定理（円周角の定理）も有向角を用いて記述できます。通常の角度の場合と変わりません。
円$ABC$の中心$O$に対し, $\mang AOB=2\mang ACB$
平行線
$AB\parallel CD$ならば, $\mang ABC+\mang BCD=0$
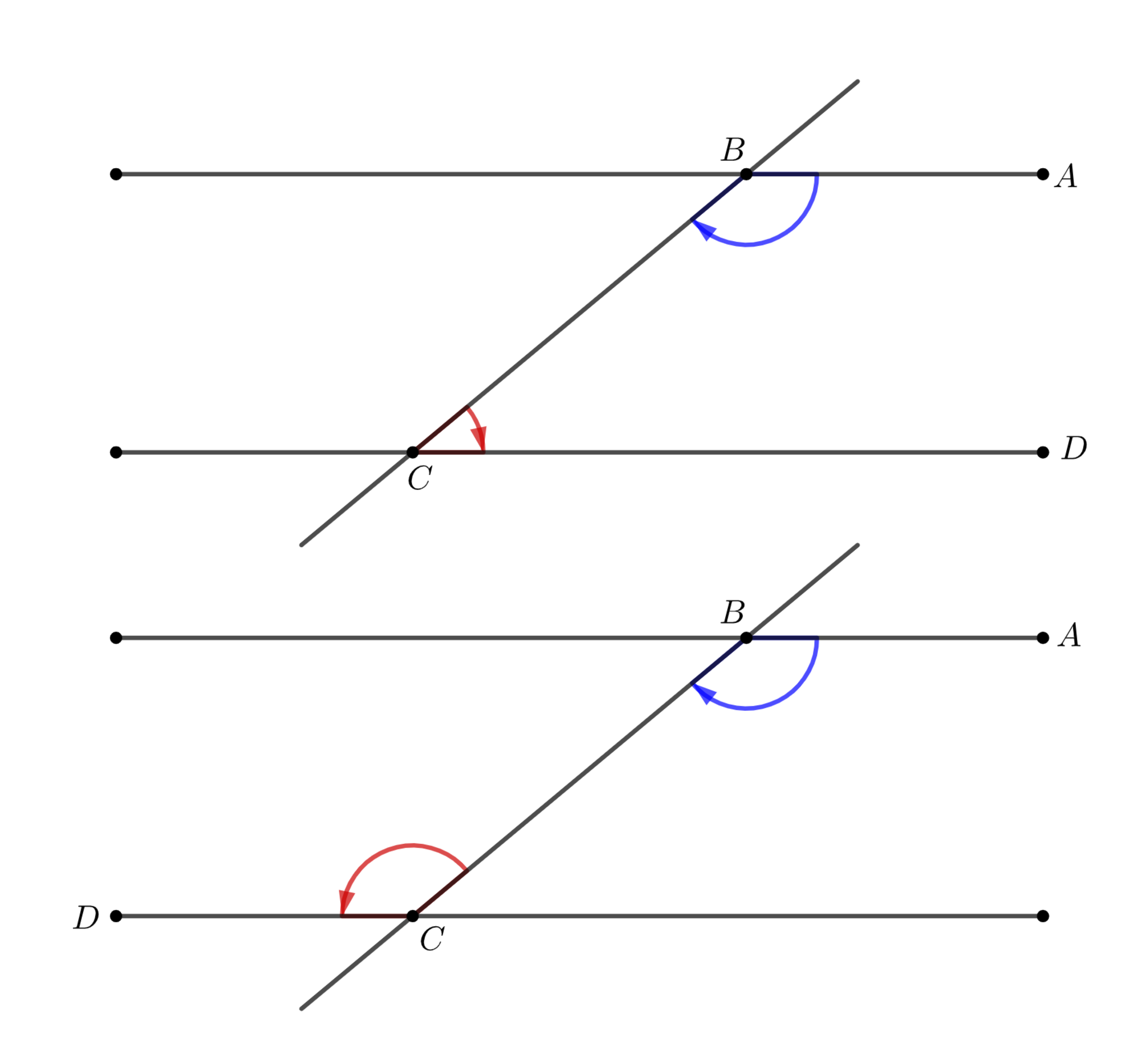定理11
接弦定理
円$ABC$と点$P$があり, $AP$は$P$で円$ABC$に接している. このとき, $\mang PAB=\mang ACB$である.
通常の接弦定理と同様なので略.
有向角ならではの注意
通常の角度では許されているが有向角に対しては許されていない操作があります。
有向角において, $2\mang ABC=2\mang XYZ$であっても$\mang ABC=\mang XYZ$とは限らない. 例えば, $\mang ABC=30\do, \mang XYZ=120\do$などが反例である.
これは合同式の両辺を割る操作が許されていないことと同様です。有向角における等号は$\mathrm{mod}180\do$での等号であることは念頭に入れておきましょう。
有向角の使用例
有向角の基本性質を一通り紹介したので、次は有向角を実際に使ってみましょう。
ミケルの三角形定理
この記事の最初にあったミケルの三角形定理の証明を有向角を用いて正しく書きなおします。
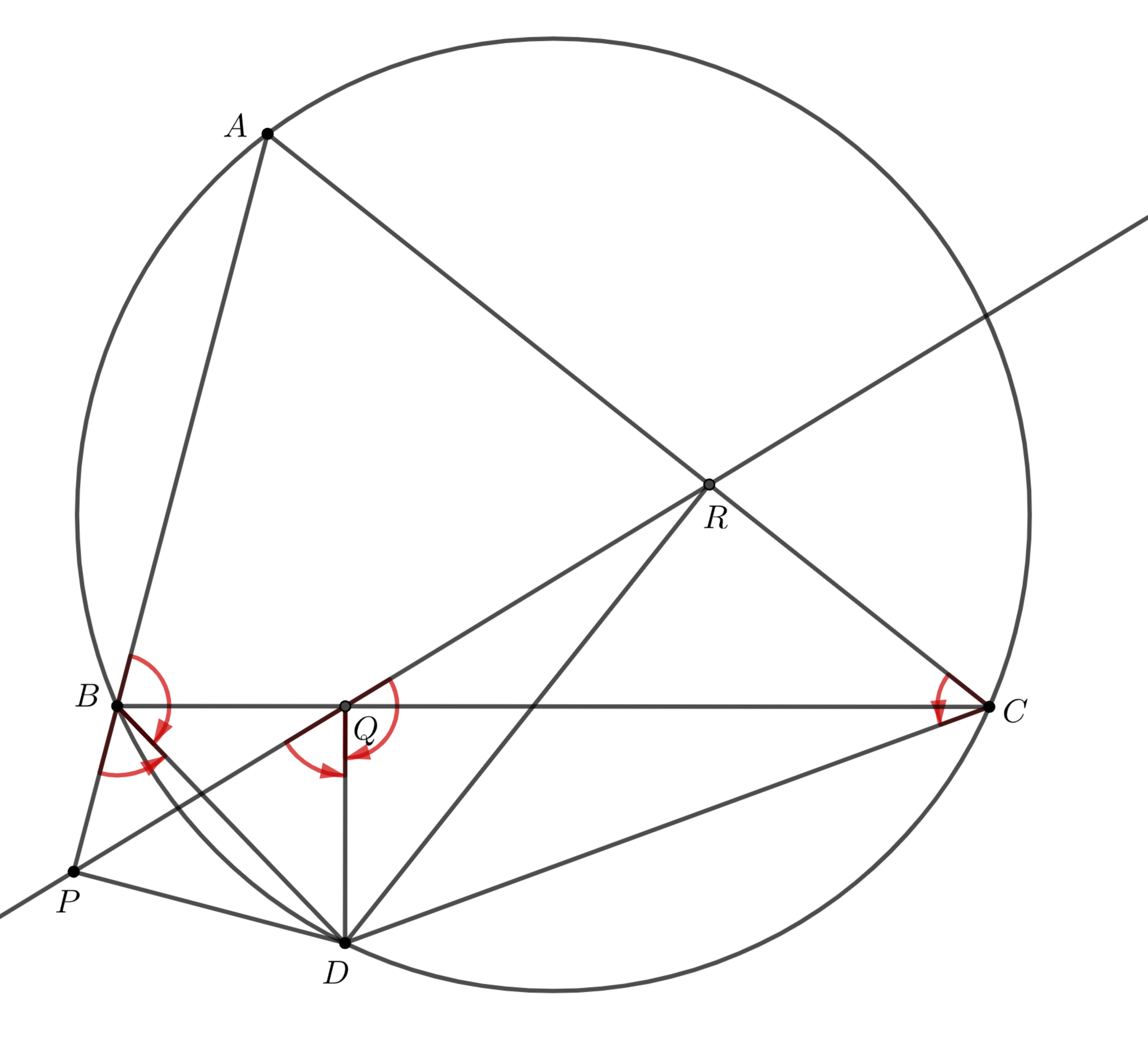
三角形$ABC$がある. 直線$BC,CA,AB$上にそれぞれ点$D,E,F$をとるとき, 円$AEF,BDE,CDF$は1点$P$で交わる. この$P$をミケル点という.
円$AEF,BDE$の交点を$P$とする. 4点$CPDF$の共円を示せばよい.
円$APEF$について, $\mang CDP=\mang BEP$ （定理4より）
円$BPDE$について, $\mang BEP=\mang PFA$ （定理4より）
よって, $\mang CDP=\mang PFA$
従って, 定理7より4点$CPDF$は共円であるから主張は従う.
この証明は以下の3つの図のうちどの場合でも成立します。時計回りか、反時計回りかに意識して角度を追ってみてください。
また、参考程度に$D,E,F$を$A,B,C$に近づけるとミケル点$P$はブロカール点に収束します。
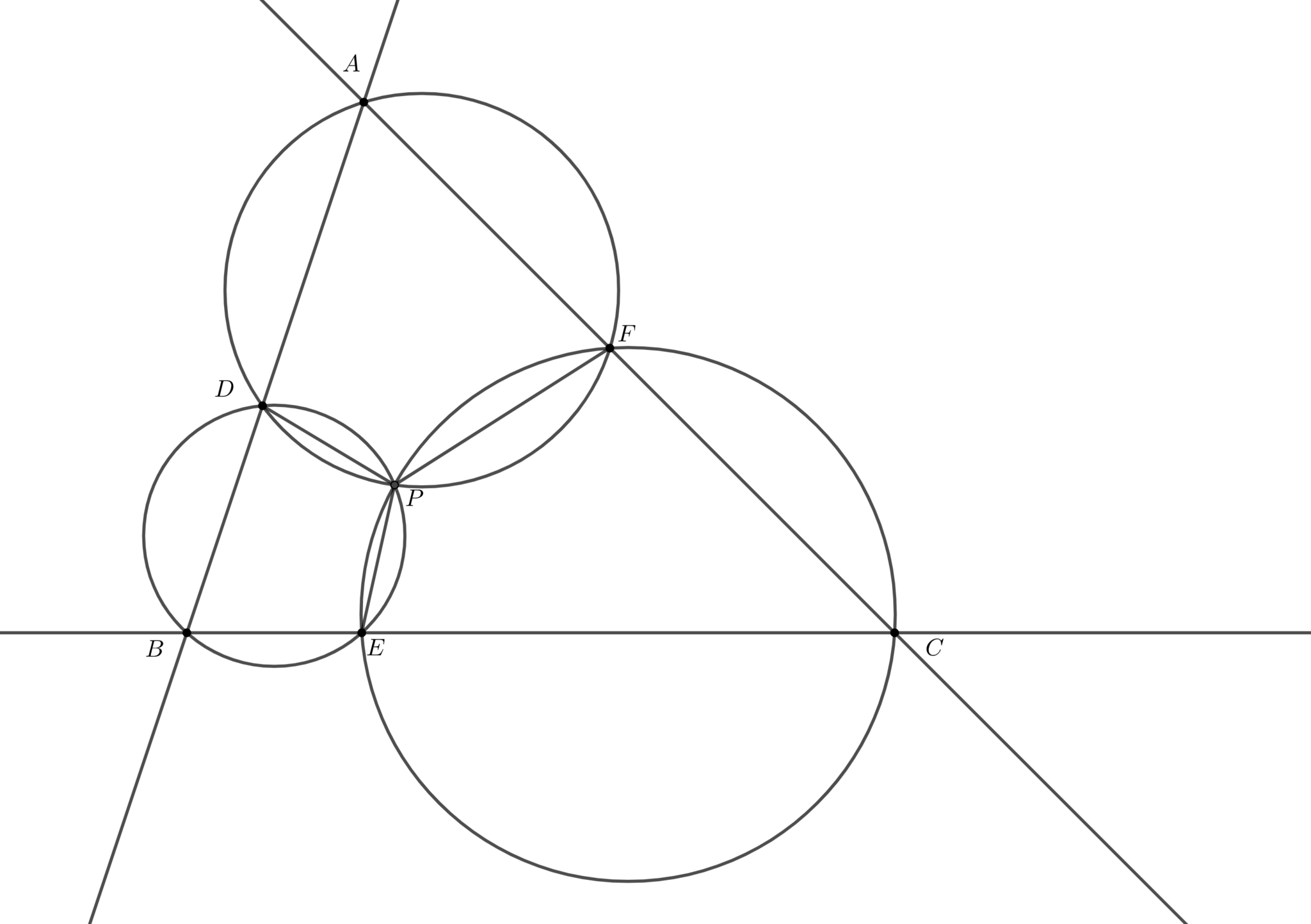定理13（その1）
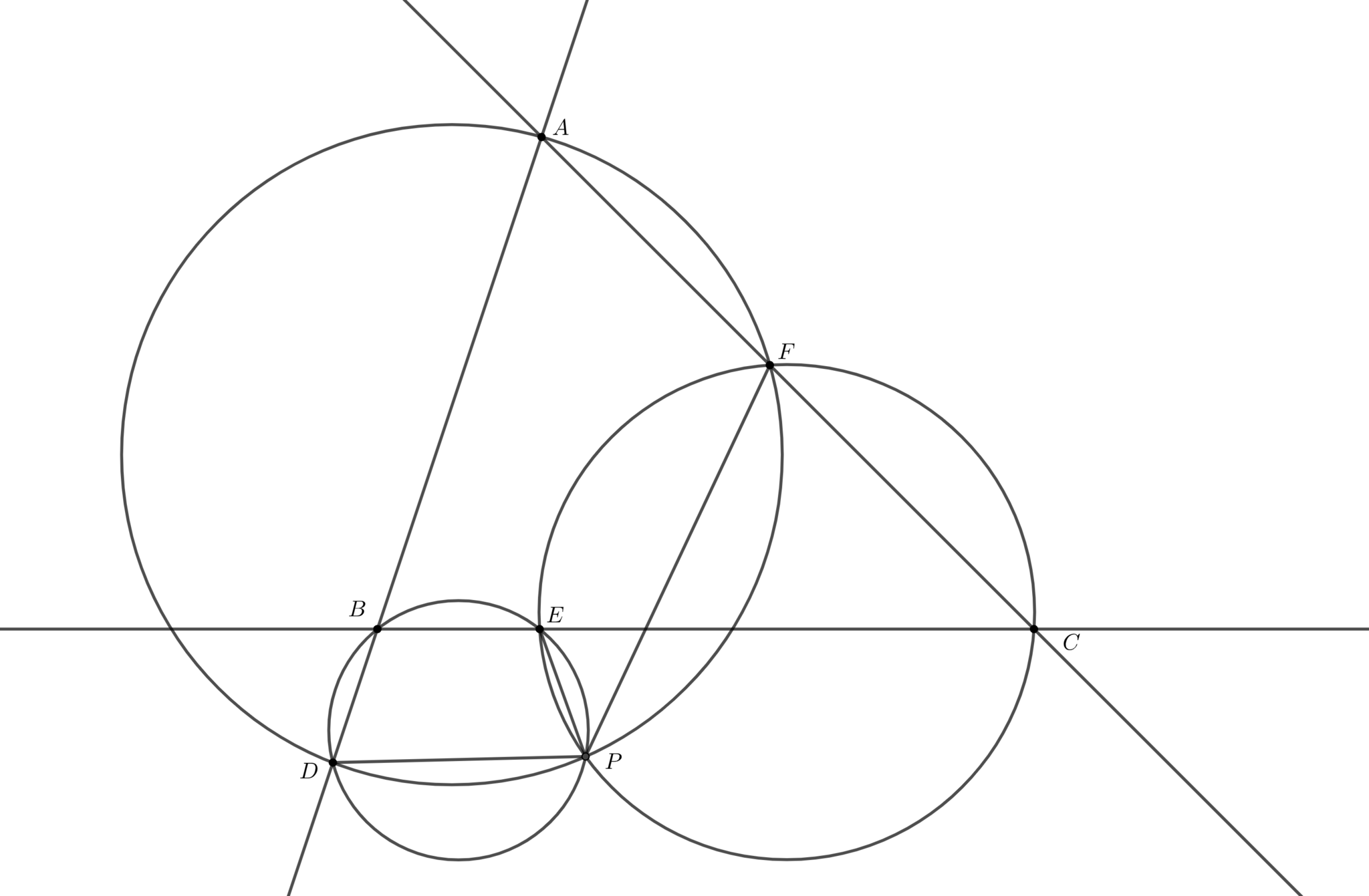定理13（その2）
定理13（その3）
シムソンの定理
次に有向角を用いてシムソンの定理を証明します。
三角形$ABC$とその外接円上に点$D$がある. $D$から直線$AB,BC,CA$に下した垂線の足をそれぞれ$P,Q,R$とするとき, 3点$P,Q,R$は同一直線上にある. この3点を通る直線をシムソン線 (Simson Line)という.
$\mang PQR=0$を示せばよい.
$\mang BPD=\mang PQD=90\do, \mang CQD=\mang CRD=90\do$より,
4点$BDPQ,CDQR$はそれぞれ共円.
$$
\begin{eqnarray*}
\mang PQR &=& \mang PQD+\mang DQR \\
&=& \mang PBD+\mang DCR \\
&=& \mang ABD+\mang DCA \\
&=& \mang ABD-\mang ACD \\
&=& 0
\end{eqnarray*}
$$
従って, 主張は従う.
定理14
図17では$P,Q$が$BD$に対して異なる側にある場合のみが示されていますが、$P,Q$が$BD$に対して同じ側にあるような図でも証明が破綻しないことを確認してみてください。
シムソンの定理は逆も成り立ちます。逆も有向角を用いて証明が記述できますので興味のある方は書いてみてください。また、シムソンの定理にはいくつもの興味深い拡張が存在しますが、それを紹介するのはこの記事の目的でないので割愛させていただきます。
向きの付いた相似（2021.2.11追記）
ここまで、有向角によって円周りの定理の記述が簡潔になることを見てきました。しかし、有向角を用いて合同や相似を記述しようとすると不自然になることがあります。より具体的には、頂点の対応関係が崩れてしまいます。そこで、合同と相似にも向きを付けて考えることによって、共円条件だけでなく合同や相似も有向角で扱える枠組みを整えます。
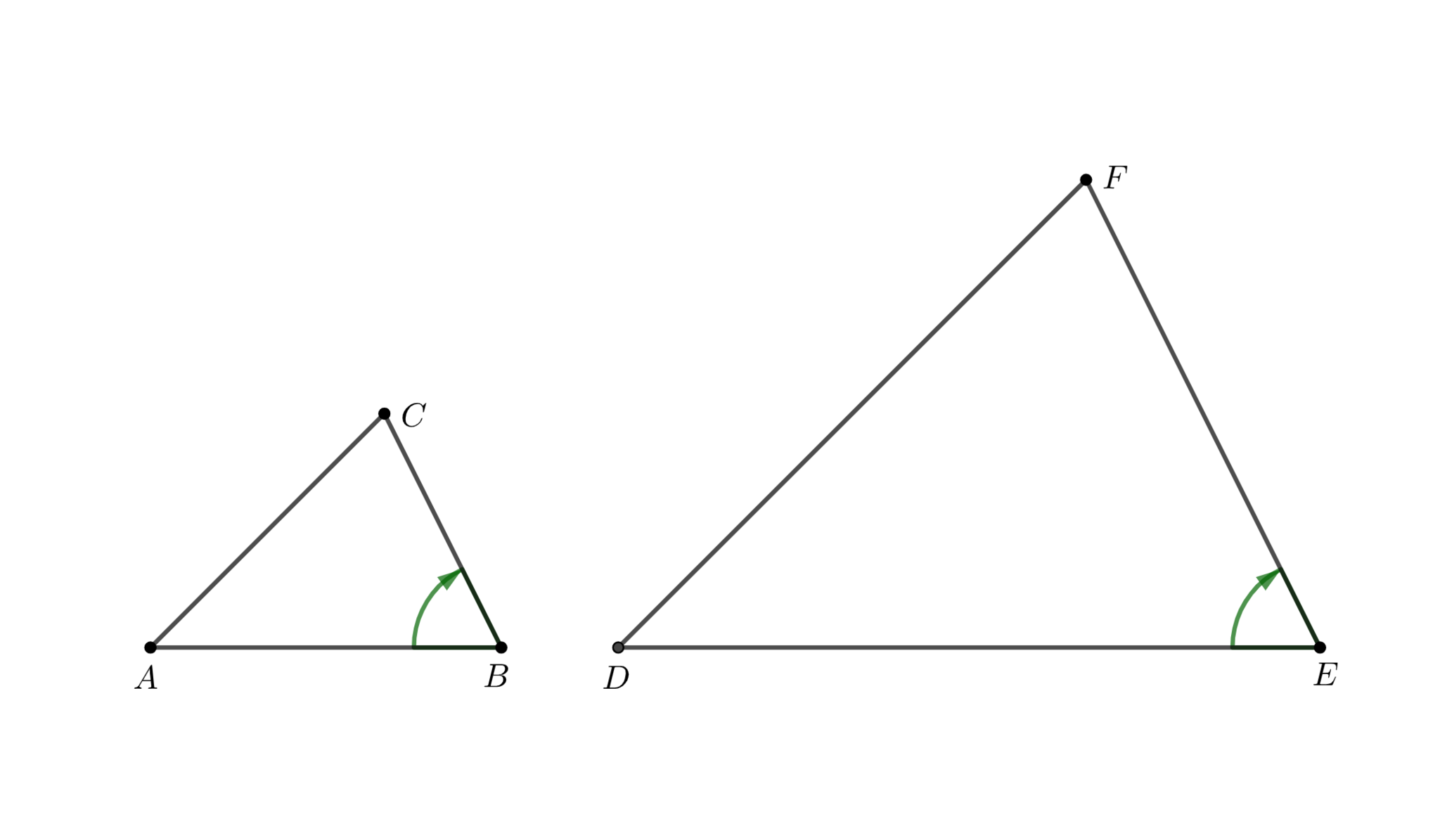
平面上に$\triangle ABC\sim DEF$なる2つの三角形$ABC,DEF$がある. これらが以下を満たすとき, 三角形$ABC$と$DEF$は正の向きに相似, または直接相似(directly similar)であると定める:
$$
\mang ABC=\mang DEF, \mang BCA=\mang EFD, \mang CAB=\mang FDE
$$
正の向きに相似とは、一方を正の倍率の相似拡大と平行移動の合成で他方に重ねることができる関係を指します。特に、正の向きに合同であることを一方を平行移動と回転移動の合成で他方に重ねることができる関係として定義します。
定義3
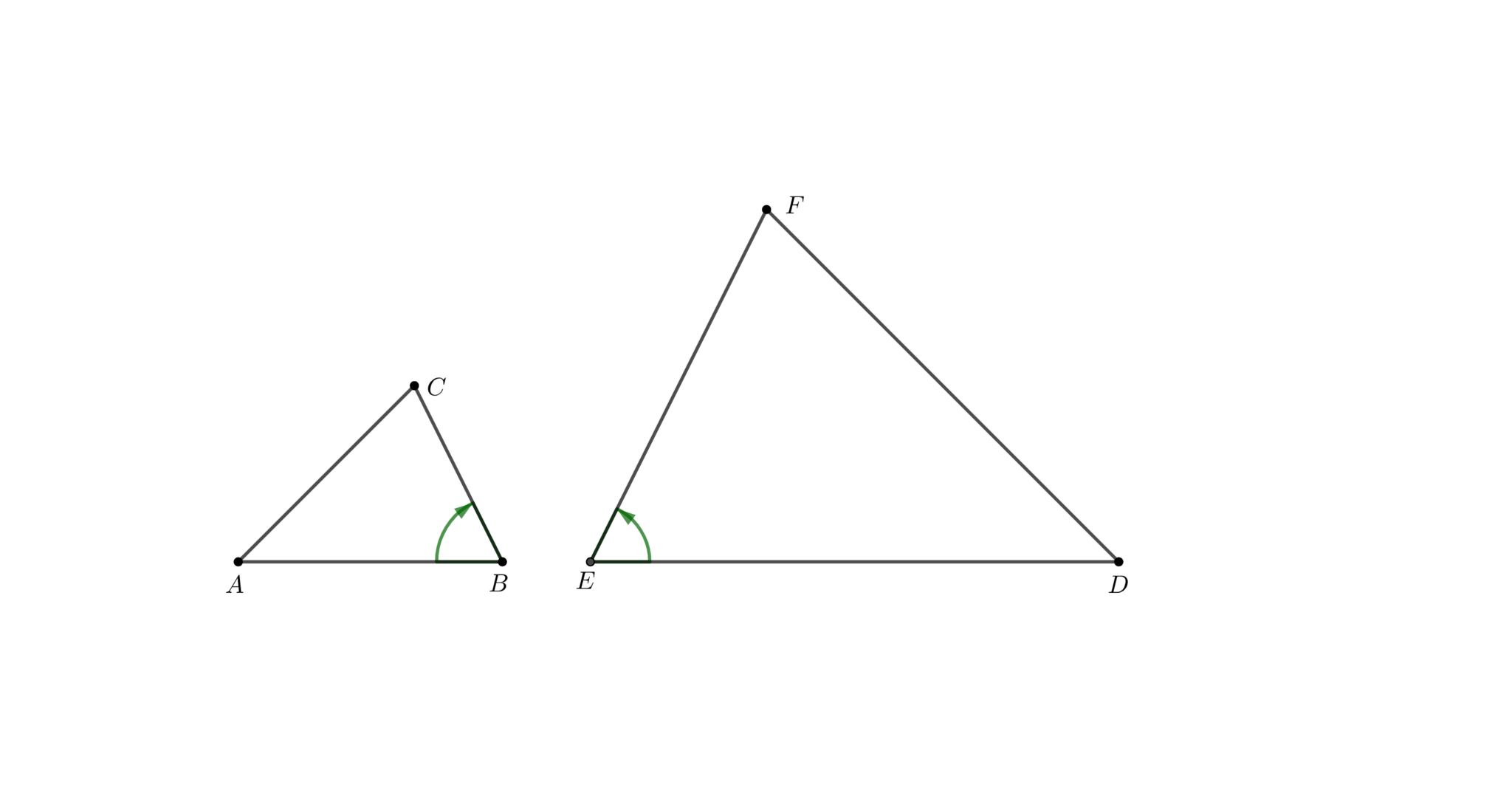
平面上に$\triangle ABC\sim DEF$なる2つの三角形$ABC,DEF$がある. これらが以下を満たすとき, 三角形$ABC$と$DEF$は負の向きに相似, または逆相似(oppositely similar)であると定める:
$$
\mang ABC=-\mang DEF, \mang BCA=-\mang EFD, \mang CAB=-\mang FDE
$$
負の向きに相似とは、一方を負の倍率の相似拡大と平行移動の合成で他方に重ねることができる関係を指します。言い換えれば、「ひっくり返した相似」です。特に、負の向きに合同であることを一方を対称移動と平行移動、回転移動の合成で他方に重ねることができる関係とした定義します。
定義4
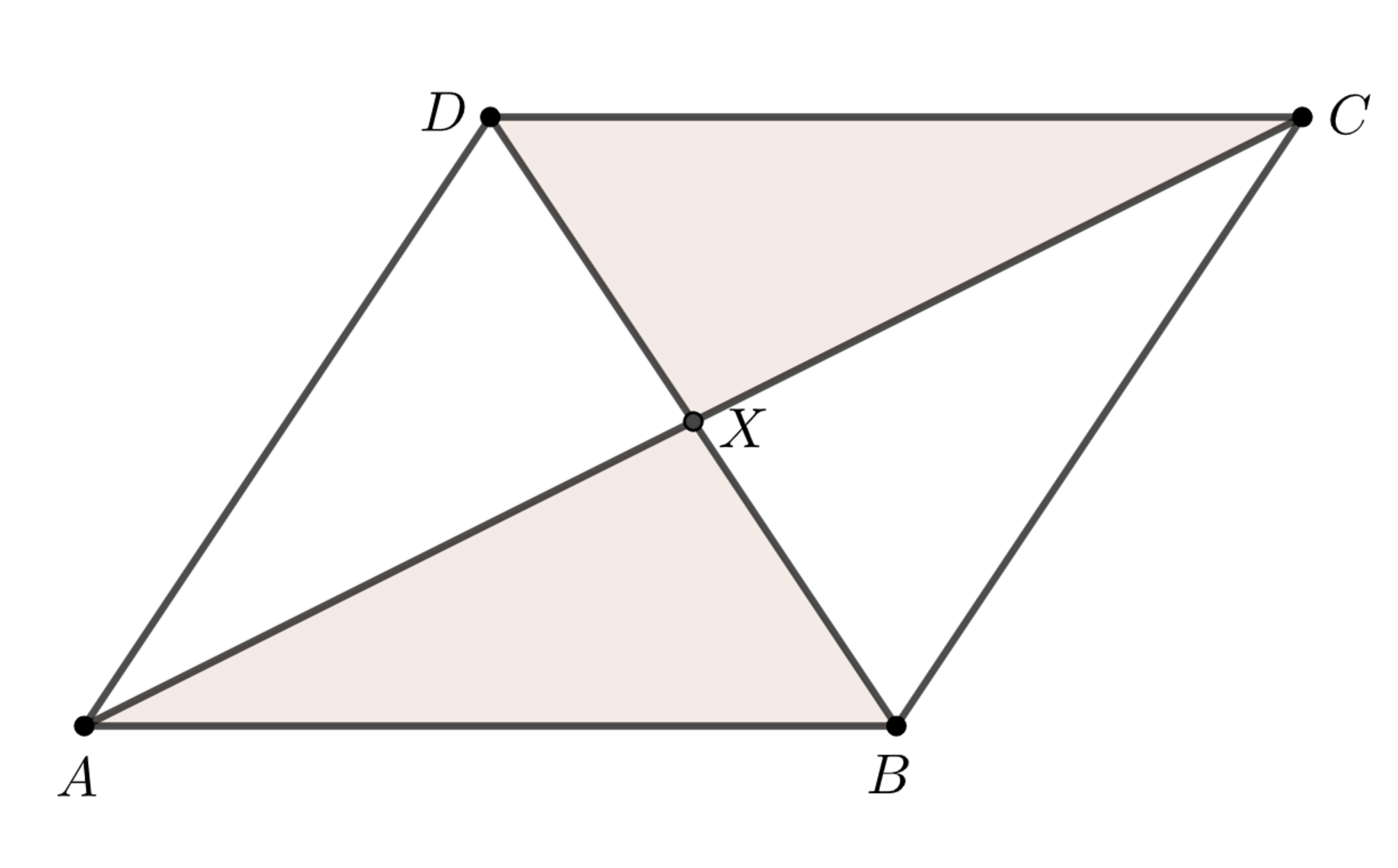
平行四辺形$ABCD$とその対角線の交点$X$について, 三角形$ABX,CDX$は正の向きに合同である.
例3
$AB=AC$なる二等辺三角形$ABC$と辺$BC$の中点$M$について, 三角形$ABM,ACM$は負の向きに合同である.
例4
三角形$ABC$と辺$AB,AC$の中点$M,N$について, 三角形$AMN,ABC$は正の向きに相似である.
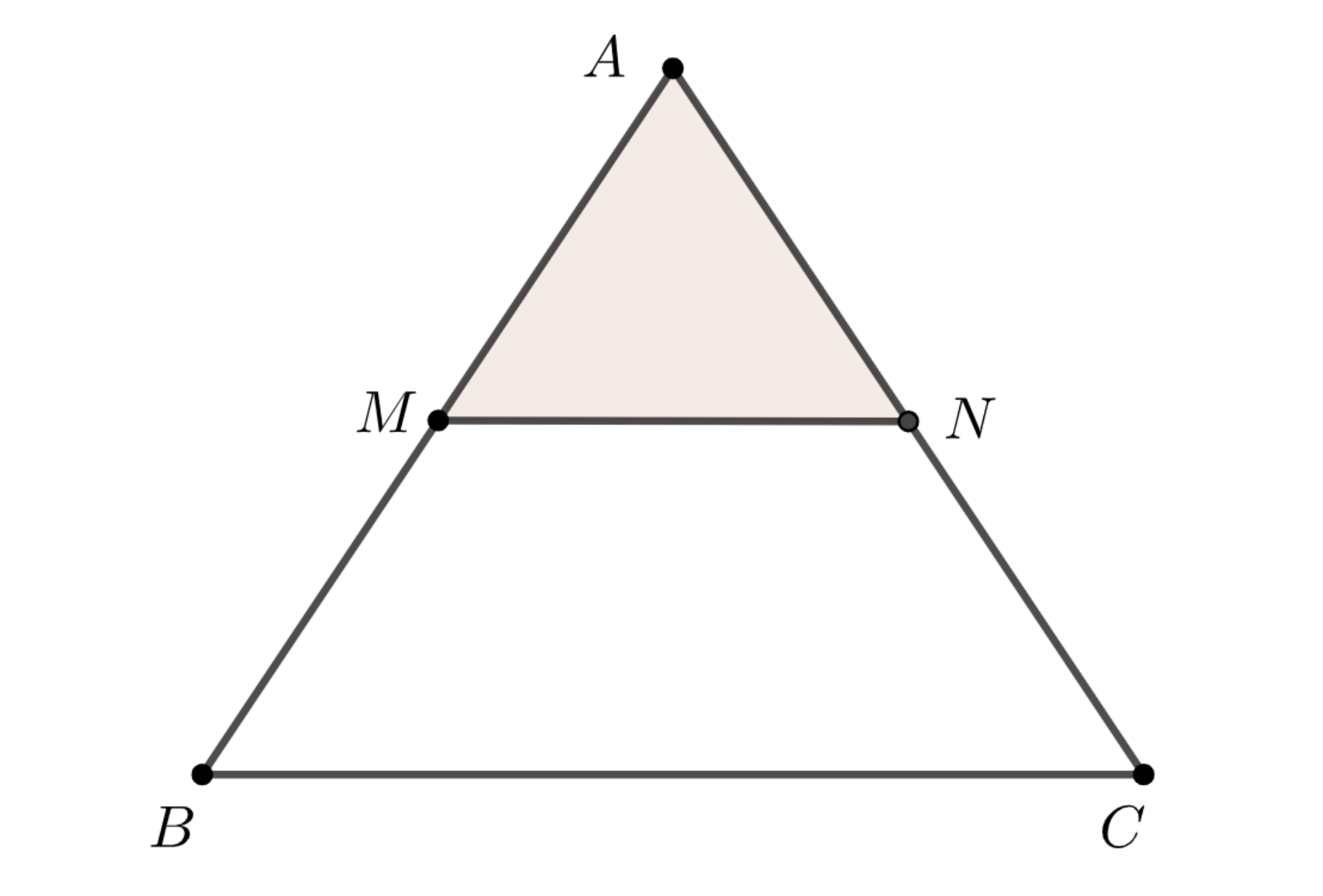例5
円に内接する四角形$ABCD$とその対角線の交点$X$について, 三角形$ABX,DCX$は負の向きに相似である.
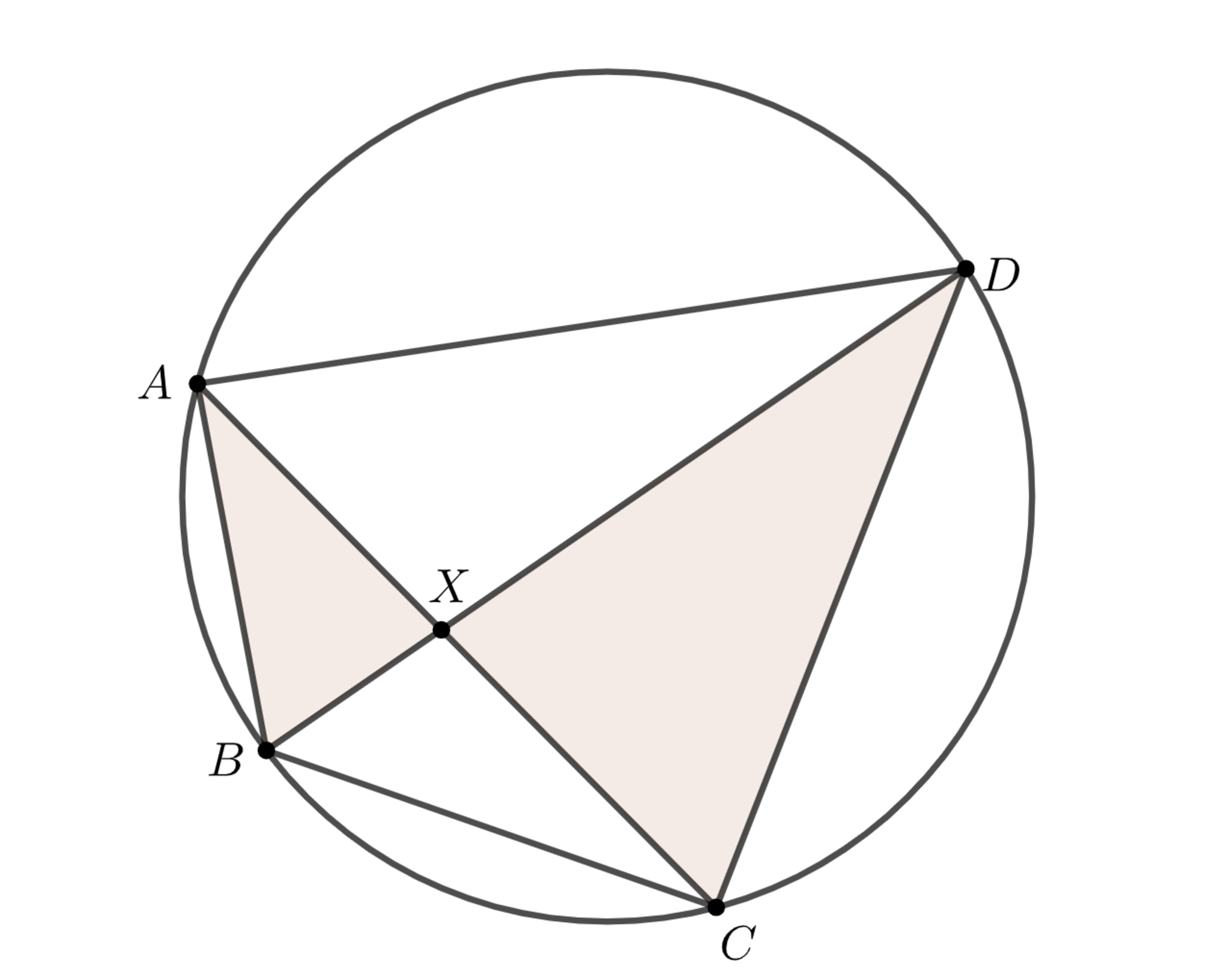例6
おわりに
最後まで読んでくださりありがとうございました。この記事が共に数学オリンピックを目指す方々のお役に立てれば幸いです。これからも初等幾何の解説記事を書いていこうと思います。
