幾何的に見る放物線
この記事では,従来,円と直線を主に扱う初等的(座標や複雑な計算を用いない)な幾何に,対象図形として「放物線」を加えてみたいと思う．
数Ⅰまでの放物線というと通常$y=ax^2+bx+c$で表される曲線であるが,本稿の趣旨にそって,数Ⅲのより図形的な定義を用いて,以下の議論を進める．
もちろん$y=ax^2+bx+c$を用いても同じ結果が得られる(道具として図形の方程式,微分が使える)．
放物線の定義
平面上の点$F$および直線$l$に対して次の条件を満たす点$P$の集合を,放物線と呼び,点$F$および直線$l$をそれぞれこの放物線の焦点,準線と呼ぶ．
条件：$P,F$の距離と$P,l$の距離が等しい
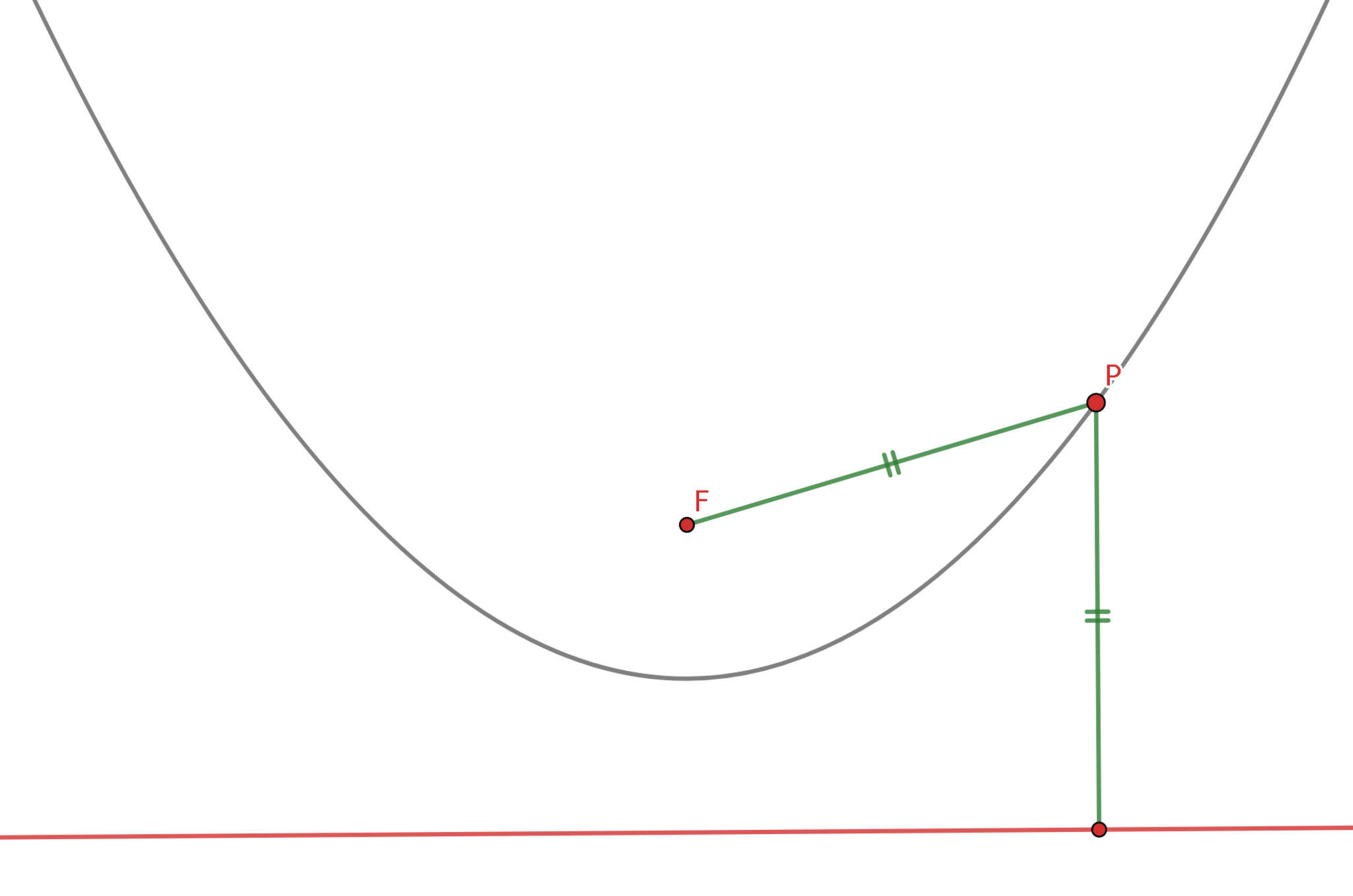放物線の定義
問題集(有名事実)
以下,点$F$,直線$l$はそれぞれの焦点,準線とする．
放物線上に2点$A,B$があり,$AB$と$l$は平行でないとする．
直線$AB$と$l$の交点を$P$とすると直線$FP$は$\angle AFB$の外角を二等分することを示せ．
放物線上に点$A$があり,$A$での放物線の接線と$l$は平行でないとする．
$A$から$l$に下ろした垂線の足を$A^{\prime}$とする．
このとき$A$での放物線の接線は$\angle FAA^{\prime}$を二等分することを示せ．
点$T$から放物線に接線を2本引くことができるとき,接点を$A,B$とする．次の(1),(2),(3)を示せ．
(1)線分$AB$を中点$M$とすると,$TM\perp l$
(2)$\triangle FTA$と$\triangle FBT$は相似
(3)点$T$が$l$上にあるとき,$F$は線分$AB$上にあり,$\angle ATB=90^{\circ}$
この3つが主要な定理,補題となる．
自作問題
点$F$,直線$l$はそれぞれの焦点,準線とする．
放物線上に点$A,B,C,D$があり,$AB/\!/CD$を満たす．
直線$AC,BD$の交点,直線$AD,BC$の交点をそれぞれ$X,Y$とする。$XY\perp l$を示せ．
点$T$から放物線に接線を2本引くことができるとき,接点を$A,B$とする．
$A,B$から$l$に下ろした垂線の足をそれぞれ$A^{\prime},B^{\prime}$とする．
三角形$TAB$の外接円の半径を$R$としたとき$AB\cdot FT=R\cdot A^{\prime}B^{\prime}$を示せ．
終わりに
この記事で紹介した性質はほんの一部です．
「放物線 初等幾何」などで検索をかけるとさまざまな美しい定理がヒットするのでぜひ調べてみてください．ほかの二次曲線に対しても初等的なアプローチをしてみたいですね．
時間があればですが問題の想定解もまとめたいと思っています．
拙い文章でしたが,記事を読んでいただきありがとうございました．
この記事を高評価した人
この記事に送られたバッジ
投稿者
