正多角形の対角線の交点の数について(GIFあり)

はじめに
論文の紹介
きっかけのツイート
交点の数の上限
正多角形の対角線の交点の数の上限は二項係数でわかる
正多角形の対角線の交点の数の公式
公式を分解する
正 $30$ 角形は特別
対角線で分割される領域数を数える
論文での証明のアイデア
$3$ 本の対角線が共点となる条件
三角関数版ディオファントス方程式
複素数の不定方程式を作る
さらに一般化して考える
おまけ(チェバの定理との関係)
おわりに
参考文献

高校数学解説

文献あり

正多角形の対角線の交点の数について(GIFあり)

GIF,正多角形,日曜数学会

1216

はじめに

　この記事は $2022$ 年 $1$ 月 $22$ 日に開催された日曜数学会で私が発表した内容についての記事です。

　私のTwitterのフォロワー $2500$ 人記念で正多角形の対角線の交点の数に関連する問題を出題したときに見つけた論文の内容について、なかなか興味深い内容でしたので、私はまだ証明の部分は完全には理解できていないですが、理解できた範囲についてご紹介したいと思います。

論文の紹介

　まずは、論文のご紹介から。

(arxiv)Bjorn Poonen, Michael Rubinstein:The Number of Intersection Points Made by the Diagonals of a Regular Polygon(1995)

　この論文は、正 $n$ 角形の対角線の交点の数を完全に解析して、 $n$ の式で表すことができたというものです。さらにその系として、対角線で分割される領域の数も $n$ の式で表しています。

　実際にやってみるとわかりますが、任意の正 $n$ 角形の対角線の交点の数を求めることは非常に難しいです。この論文は $1995$ 年に発表されたもので、 $2006$ 年にv3版にアップデートされています。

　つまり、今から $27$ 年前に公式ができた、ということです。割と最近まで公式化されていなかったということで、このことからも、この問題がなかなか難しい問題であることがわかるのではないでしょうか。

きっかけのツイート

　この論文を見つけるきっかけとなったのは次の問題を作問したときでした。

==以下引用==

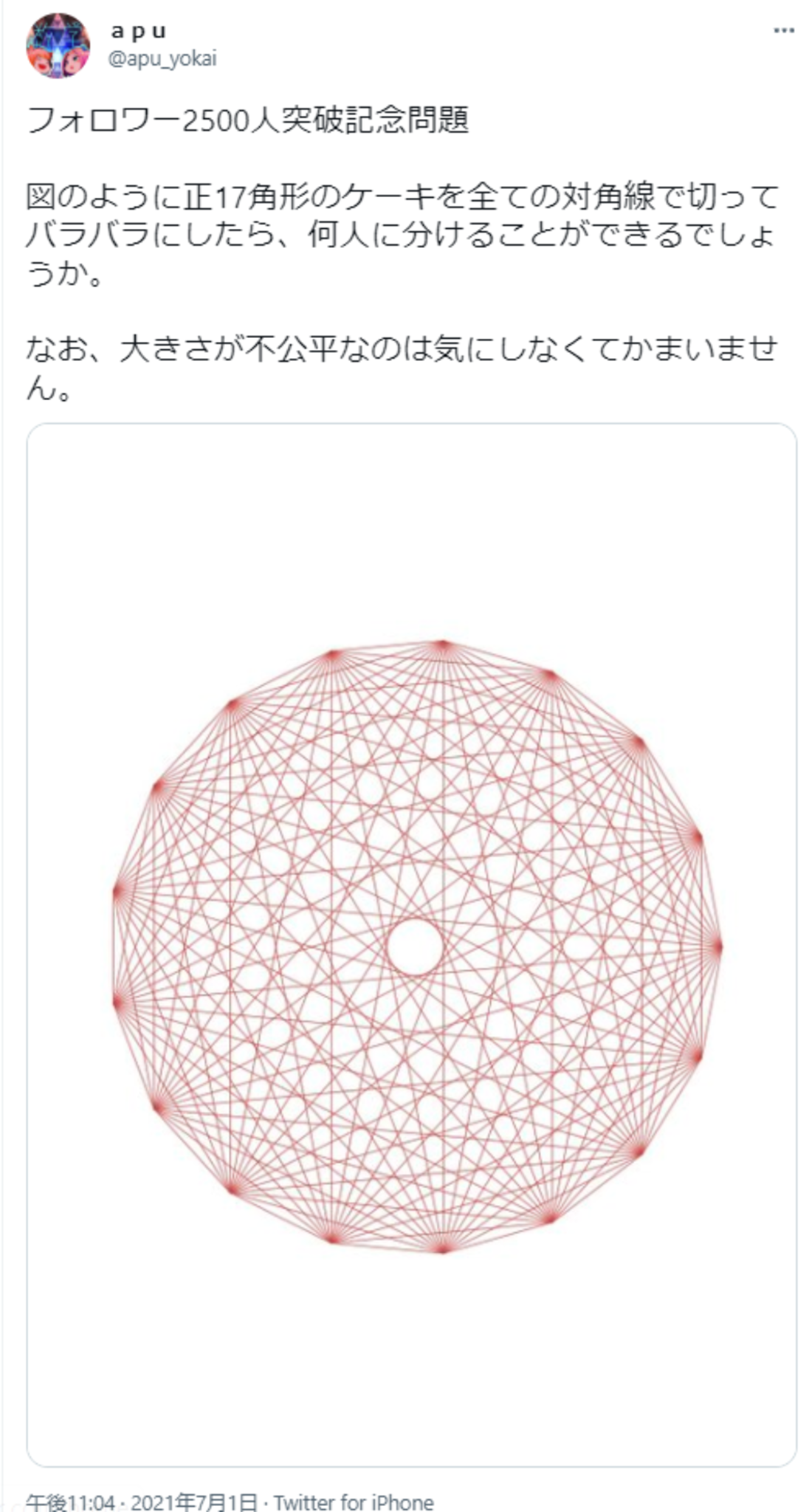
フォロワー2500人突破記念問題

図のように正17角形のケーキを全ての対角線で切ってバラバラにしたら、何人に分けることができるでしょうか。

なお、大きさが不公平なのは気にしなくてかまいません。 pic.twitter.com/c2kpK01MRS
— ａｐｕ (@apu_yokai) July 1, 2021

きっかけのツイート

==引用おわり==

交点の数の上限

　正 $17$ 角形を対角線でバラバラにするといくつの領域に分かれるか、という問題です。

　正 $17$ 角形の対角線の交点の数がわかれば、それをもとに領域の数を計算できるので、まず対角線の交点の数を計算する必要があります。

　そして、正 $17$ 角形の対角線の交点の数は、「 $n$ が奇数のとき、正 $n$ 角形について $3$ 本以上の対角線が共点となる( $1$ 点で交わる)ことはない」という性質を使えば手計算できます。

　この記事を最後まで読めばこの問題の答えがわかるはずですので、ここではこの問題はいったん棚に上げておいて、一般化した「正(奇数)角形の対角線の交点の数」の計算方法について解説したいと思います。

正多角形の対角線の交点の数の上限は二項係数でわかる

　正 $n$ 角形の頂点を $4$ つ選ぶと、対角線の交点が $1$ つ対応することから、 $(\binom{n}{4})$ は交点の数の上限になります。 $n$ が奇数のときは $3$ 本以上の対角線が共点となることはないことから、上限はそのまま実際の対角線の数となります。
※　 $(\binom{n}{4})$ は二項係数の表し方の一つです。つまり $(\binom{n}{4}) =_{n} C_{4}$

対角線の交点の数の上限 $= (\binom{n}{4})$

nが奇数のときの対角線の交点の数 $= (\binom{n}{4})$

4つの頂点を選ぶと1つの交点が対応する

　 $n$ が偶数のときは、 $3$ 本以上の対角線が共点となることがありますので、 $(\binom{n}{4})$ は交点の数の上限にはなりますが、実際の交点の数はこれより少なくなります。

正多角形の対角線の交点の数の公式

　 $n$ が奇数のときは対角線の交点の数は簡単にわかるのですが、偶数のときはとても難しいです。
　偶数のときは $3$ 本以上の対角線が $1$ 点で交差することがあるのですが、そのパターンが非常に多くて調べ上げるのがすごく大変なのです。

　しかし、上記の論文ではそのすべてのパターンを調べ上げて公式を作ったのです。
　まずは、論文で紹介されている公式をご紹介します!
　ここからは、 $I (n)$ で正 $n$ 角形の対角線の交点の数を表します。また、 $δ_{m} (n)$ は $n$ が $m$ の倍数のとき $1$ 、それ以外のときは $0$ となる関数です。

$\begin{aligned} I (n) = & (\binom{n}{4}) + \frac{- 5 n^{3} + 45 n^{2} - 70 n + 24}{24} \cdot δ_{2} (n) \\ - \frac{3 n}{2} \cdot δ_{4} (n) + \frac{- 45 n^{2} + 262 n}{6} \cdot δ_{6} (n) \\ + 42 n \cdot δ_{12} (n) + 60 n \cdot δ_{18} (n) \\ + 35 n \cdot δ_{24} (n) - 38 n \cdot δ_{30} (n) \\ - 82 n \cdot δ_{42} (n) - 330 n \cdot δ_{60} (n) \\ - 144 n \cdot δ_{84} (n) - 96 n \cdot δ_{90} (n) \\ - 144 n \cdot δ_{120} (n) - 96 n \cdot δ_{210} (n) \end{aligned}$

$δ_{m} (n) = {\begin{cases} 1 & if n \equiv 0 (\mod m), \\ 0 & otherwise. \end{cases}$

$n$ に具体的な値を代入して計算すると次のようになります。


$n$	3	4	5	6	7	8	9	10	$\dots$
$I (n)$	0	1	5	13	35	49	126	161	$\dots$

公式を分解する

もう少しくわしく、公式をみていきましょう。
実は、先ほどの公式を次のように分解することができます。
ここで、 $a_{k} (n)$ は、正 $n$ 角形のちょうど $k$ 本の対角線が中心以外の場所で交わる点の数を表しています。

$I (n) = δ_{2} (n) + a_{2} (n) + a_{3} (n) + a_{4} (n) + a_{5} (n) + a_{6} (n) + a_{7} (n)$

$\begin{aligned} a_{2} (n) = & n (\frac{n^{3} - 6 n^{2} + 11 n - 6}{24} + \frac{- 5 n^{2} + 46 n - 72}{16} d_{2} (n) - \frac{9}{4} d_{4} (n) + \\ + \frac{- 19 n + 110}{2} d_{6} (n) + 54 d_{12} (n) + 84 d_{18} (n) + 50 d_{24} (n) - 24 d_{30} (n) - 100 d_{42} (n) \\ - 432 d_{60} (n) - 204 d_{84} (n) - 144 d_{90} (n) - 204 d_{120} (n) - 144 d_{210} (n)) \end{aligned}$
$\begin{aligned} a_{3} (n) = & n (\frac{5 n^{2} - 48 n + 76}{48} d_{2} (n) + \frac{3}{4} d_{4} (n) + \frac{7 n - 38}{6} d_{6} (n) \\ - 8 d_{12} (n) - 20 d_{18} (n) - 16 d_{24} (n) - 19 d_{30} (n) + 8 d_{42} (n) \\ + 68 d_{60} (n) + 60 d_{84} (n) + 48 d_{90} (n) + 60 d_{120} (n) + 48 d_{210} (n)) \end{aligned}$
$\begin{aligned} a_{4} (n) = & n (\frac{7 n - 42}{12} d_{6} (n) - \frac{5}{2} d_{12} (n) - 4 d_{18} (n) + 3 d_{24} (n) + 6 d_{42} (n) \\ + 34 d_{60} (n) - 6 d_{84} (n) - 6 d_{120} (n)) \end{aligned}$
$a_{5} (n) = n (\frac{n - 6}{4} d_{6} (n) - \frac{3}{2} d_{12} (n) - 2 d_{24} (n) + 4 d_{42} (n) + 6 d_{84} (n) + 6 d_{120} (n))$
$a_{6} (n) = n (4 d_{30} (n) - 4 d_{60} (n))$
$a_{7} (n) = n (d_{30} (n) + 4 d_{60} (n))$

$I (n)$ のそれぞれの項の意味は次のようになります。

$I (n) = \underset{中心の交点の数}{\underset{⏟}{δ_{2} (n)}} + \underset{ちょうど2～7本の対角線の交点(中心除く)の数}{\underset{⏟}{a_{2} (n) + a_{3} (n) + a_{4} (n) + a_{5} (n) + a_{6} (n) + a_{7} (n)}}$

この式をよく見ると、いろいろなことがわかります。

・中心を除くと対角線は最大 $7$ 本が共点となる。 $8$ 本以上が共点となることはない。
・中心以外で $7$ 本が共点となるのは $n$ が $30$ の倍数のとき
・中心以外で $6$ 本が共点となるのは $n$ が $30$ の倍数であって $60$ の倍数でないとき
・ $n$ が $6$ の倍数でないときに中心以外で共点となる対角線は最大 $3$ 本
・ $n$ が奇数のときに共点となる対角線は最大 $2$ 本

上記の式は複雑そうに見えるかもしれませんが、これらのことは簡単に確認できますので上記の式と見比べてみてください。

正 $30$ 角形は特別

次に、正 $30$ 角形の場合についてみてみましょう。
$n = 30$ のとき、初めて $a_{7} (n)$ がゼロでなくなります。(つまり、初めて $7$ 本の対角線が中心以外で共点となる。)
さらにこのとき、 $a_{2} (n)$ ～ $a_{7} (n)$ がすべてゼロではなくなります。
そのことを実際に確かめてみましょう。

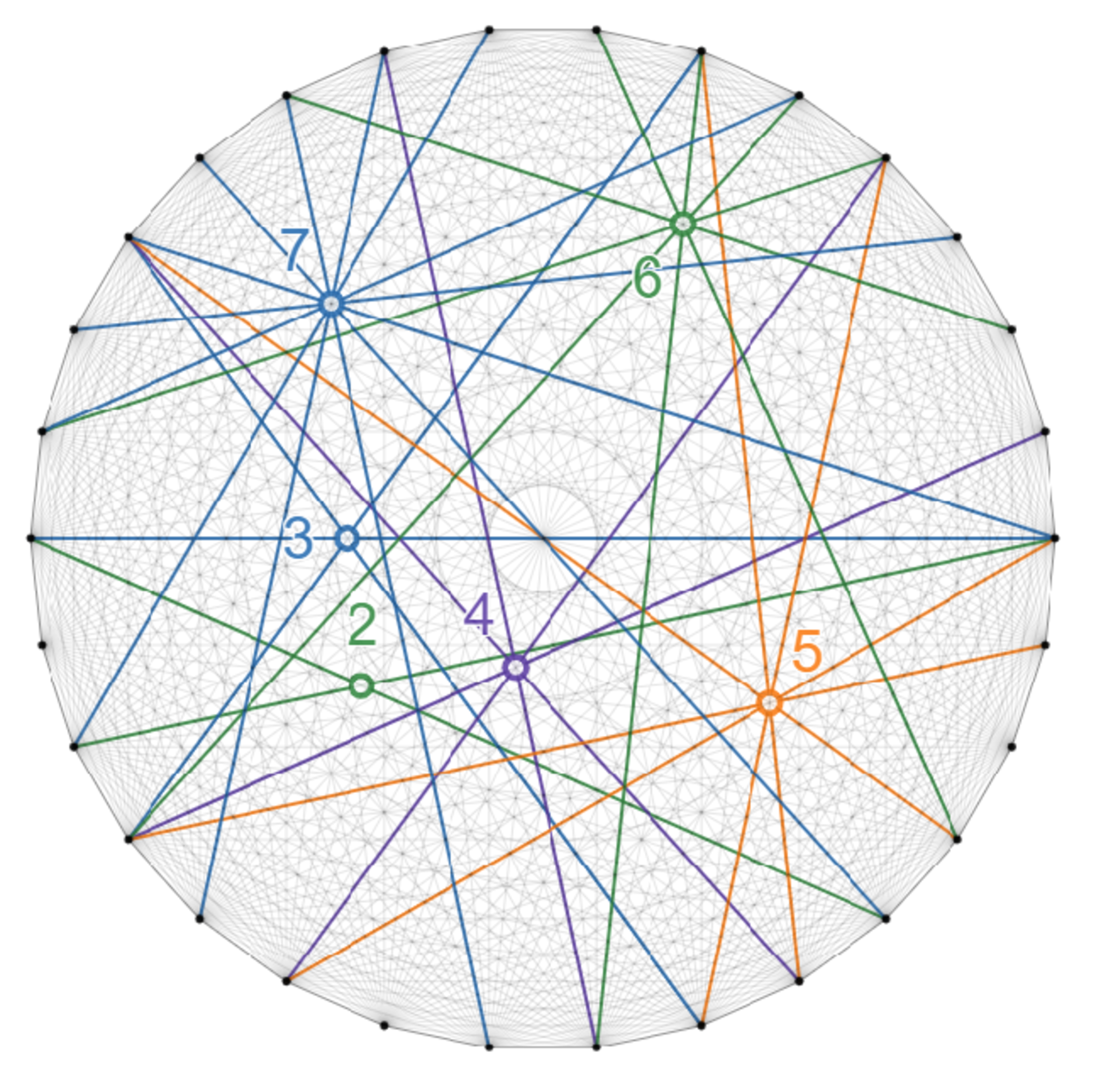正30角形の対角線2本共点～7本共点

Desmosファイルへのリンク

また、 $\frac{a_{6} (n)}{n}$ と $\frac{a_{7} (n)}{n}$ のとりうる値は次のように $2$ 種類又は $3$ 種類しかありません。

$\frac{a_{6} (n)}{n} = {\begin{cases} 4 & if n \equiv 0 (\mod 30) \land n ≢ 0 (\mod 60), \\ 0 & otherwise. \end{cases}$

$\frac{a_{7} (n)}{n} = {\begin{cases} 5 & if n \equiv 0 (\mod 60) \\ 1 & if n \equiv 0 (\mod 30) \land n ≢ 0 (\mod 60), \\ 0 & otherwise. \end{cases}$

このことは、対角線 $6$ 本以上が共点となるのは、本質的に正 $30$ 角形のときにあらわれる $5$ つのパターンしかないことを意味しています。(左辺について $n$ で割っていることに注意してください。)

具体的には、次の図の $5$ 点のみが本質的に対角線 $6$ 本以上が共点となりうる位置であり、 $n$ が $60$ の倍数のときは、対角線 $6$ 本以上共点となりうる位置は全て対角線 $7$ 本共点となるということになります。

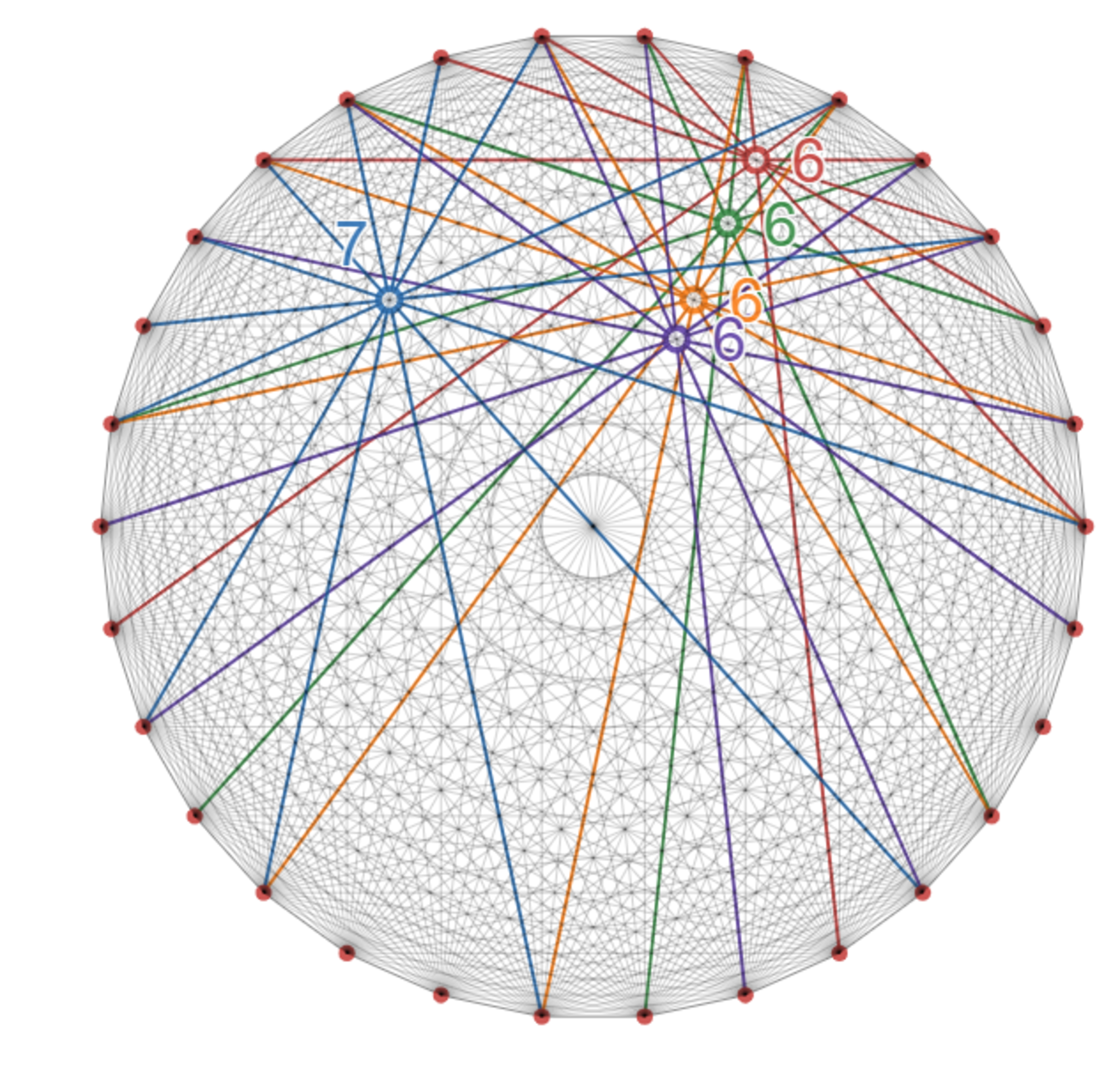対角線６本以上共点となりうる位置は本質的に5種類だけ

対角線で分割される領域数を数える

さて、先ほど対角線の交点の数を、共点となる対角線の本数ごとに分解して計算する式が得られましたので、この式を使うことで、対角線で分割される領域数を数えることができます。
ここからは、正 $n$ 角形が対角線で分割される領域の数を $R (n)$ で表すことにします。
すると、次のように計算することができます。

$\begin{aligned} R (n) = & 1 + \frac{n (n - 3)}{2} + (\frac{n}{2} - 1) δ_{2} (n) \\ + a_{2} (n) + 2 a_{3} (n) + 3 a_{4} (n) + 4 a_{5} (n) + 5 a_{6} (n) + 6 a_{7} (n) \end{aligned}$

この式の意味は次のようになります。

$\begin{aligned} R (n) = & \underset{最初の１個}{\underset{⏟}{1}} + \underset{対角線の端}{\underset{⏟}{\frac{n (n - 3)}{2}}} + \underset{正偶数角形の中心で交差}{\underset{⏟}{(\frac{n}{2} - 1) δ_{2} (n)}} \\ + \underset{中心以外の対角線の交点で交差}{\underset{⏟}{a_{2} (n) + 2 a_{3} (n) + 3 a_{4} (n) + 4 a_{5} (n) + 5 a_{6} (n) + 6 a_{7} (n)}} \end{aligned}$

次のように考えると理解できると思います。
まず、正 $n$ 角形の形のケーキを対角線に沿ってゆっくり切るところをイメージすると、他の対角線と交差するとき又は先端がケーキの端に達したときに領域が１つ増えますね。

ケーキを切る先端が他の対角線と交差するとき領域数が増える

そのことから、先端が他の対角線と交差する回数とケーキの端に達する回数を数えれば分割される領域の数がわかるというわけです。

具体的な値は次のようになります。


$n$	3	4	5	6	7	8	9	10	$\dots$
$I (n)$	0	1	5	13	35	49	126	161	$\dots$
$R (n)$	1	4	1	24	50	80	154	220	$\dots$

領域の数を数えるもう一つの方法

なお、論文の方ではこのような考え方ではなく、まず対角線の交点を多面体の頂点とみなした場合の「辺」の数を数え、オイラーの多面体定理　 $V - E + F = 2$ をあてはめるという方法で $R (n)$ を計算しています。もちろん、どちらの方法で計算しても結果は一致します。

論文での証明のアイデア

　初めに書いた通り、私は論文の内容を理解できたわけではないですが、ここからは、私がわかった範囲で論文のアイデアを紹介します。

　正多角形の対角線の交点の数についての問題を、チェバの定理の派生版を使って三角関数版ディオファントス方程式の問題に帰着して、まず $3$ 本の対角線が共点となるパターンを見つけます。そして、 $3$ 本の対角線が共点となる可能性のある配置を注意深く分析すれば、理論的には公式を導き出すのに十分な情報が得られると考えられます。しかし、それは非常に複雑であるため、まず答えの形だけを推測し，次に結果を正確に決定できるほど十分な数の計算を行った、ということのようです。

解析にあたり、円分多項式の性質やガロア群を使って効率的なアルゴリズムを作ったということのようです。

　それでも手計算では複雑な場合分けを完璧に行うことは難しかったらしく、最終的にはコンピュータの力も借りてすべてのパターンを調べ上げたそうです。

　論文によれば、実は、 $1936$ 年にもGerrit Bolという数学者が同様の方法で同様の公式を作っていたのですが、残念ながら一部の係数が誤っていたそうです。
　このことからも、容易には計算できないことが感じられますね。

　「ようです」「そうです」と続きましたが、私自身よくわかっていません。間違っていたらゴメンネ。

　ここからは、私に理解できた範囲で、論文のアイデアをもう少しかみ砕いていきます。

$3$ 本の対角線が共点となる条件

　論文のアイデアは、まず３本の対角線が共点となる条件についての問題を次の関係で式に表すというものでした。

対角線 $A D, B E, C F$ が $1$ 点で交差するとき

　　　 $\frac{A F}{F B} \cdot \frac{B D}{D C} \cdot \frac{C E}{E A} = 1$

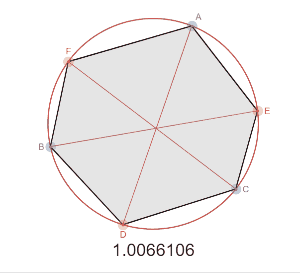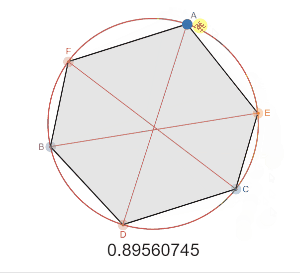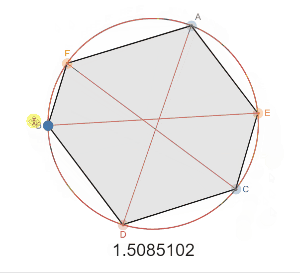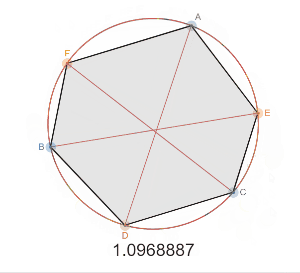弦 AD,BE,CFが 1点で交差するときAF/FB・BD/DC・CE/EA=1となる

相似を使って証明できます。

弦バージョンのチェバの定理

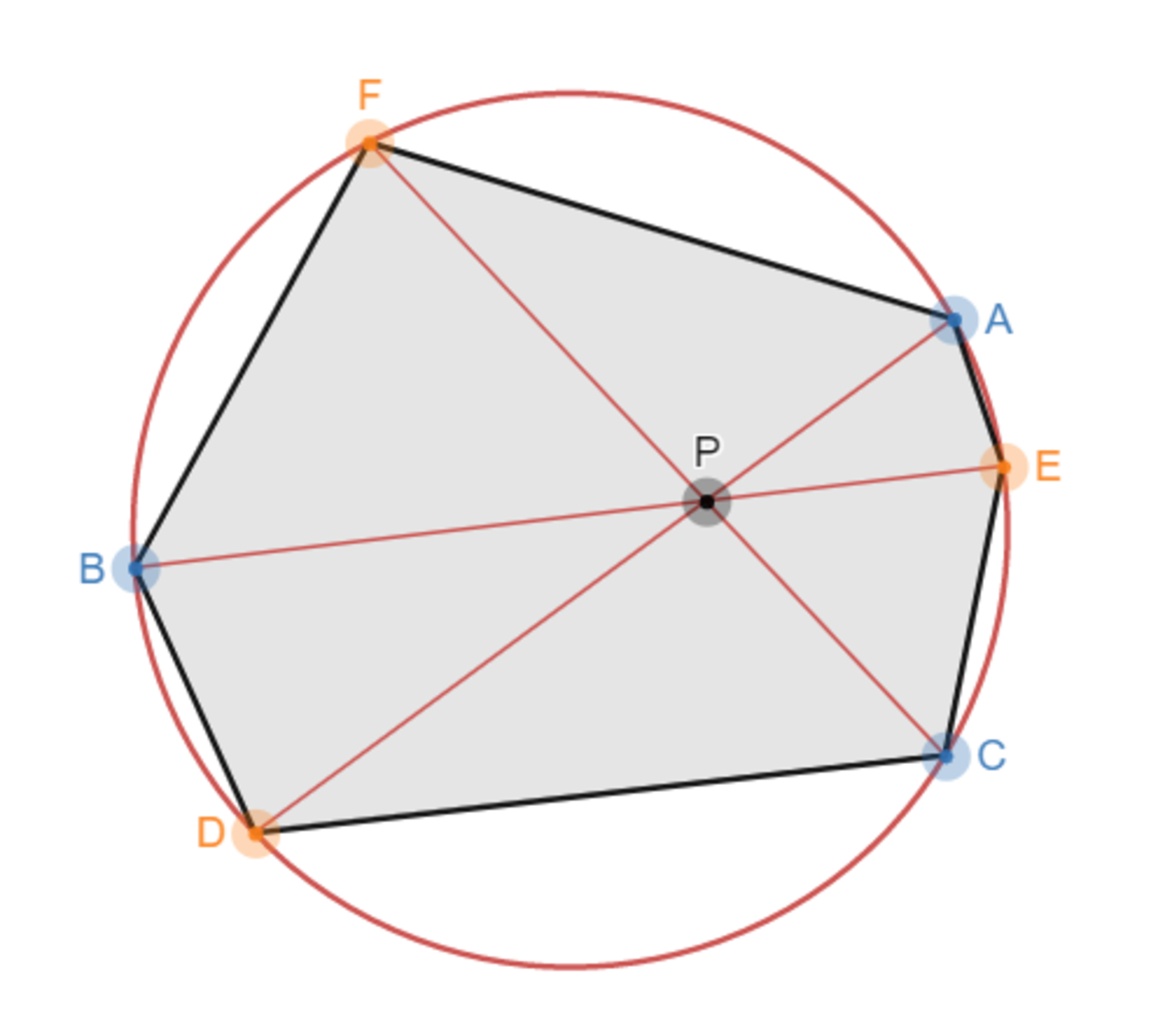AF/FB・BD/DC・CE/EA=1

$△ A F P ∽ △ C D P, △ B D P ∽ △ A E P, △ C E P ∽ △ B F P$ より

$\frac{A F}{C D} = \frac{P F}{P D}$

$\frac{B D}{A E} = \frac{P D}{P E}$

$\frac{C E}{B F} = \frac{P E}{P F}$

辺々掛け合わせて

$\frac{A F}{F B} \cdot \frac{B D}{D C} \cdot \frac{C E}{E A} = 1$

三角関数版ディオファントス方程式

　図の円の半径を $1$ (つまり単位円)とします。
　弧の長さを図のように $u, v, w, x, y, z$ として、さきほどの式を書き直します。

弧の長さを使って書き換える

$\frac{A F}{F B} \cdot \frac{B D}{D C} \cdot \frac{C E}{E A} = 1$

を $u, v, w, x, y, z$ で書き換えると

$\frac{2 \sin (x / 2)}{2 \sin (u / 2)} \cdot \frac{2 \sin (y / 2)}{2 \sin (v / 2)} \cdot \frac{2 \sin (z / 2)}{2 \sin (w / 2)} = 1$

$∴ \sin (u / 2) \sin (v / 2) \sin (w / 2) = \sin (x / 2) \sin (y / 2) \sin (z / 2)$

なお、逆も成り立つので、この式は単位円の $3$ 本の弦が共点となるための必要十分条件を与えていることになります。

さらに、 $U = \frac{u}{2 π}$ のように書き換えると、次のような不定方程式の形になります。

$\sin (π U) \sin (π V) \sin (π W) = \sin (π X) \sin (π Y) \sin (π Z)$
$U + V + W + X + Y + Z = 1$

論文ではこの不定方程式を"trigonometric diophantine equation"と呼んでいます。直訳すれば「三角関数版ディオファントス方程式」といったところでしょうか。
ここからは、この不定方程式の有理数解のパターンを分析することになります。

複素数の不定方程式を作る

先ほどの式に $\sin (θ) = \frac{e^{i θ} - e^{- i θ}}{2 i}$ を使い、両辺に $(2 i)^{3}$ を掛けて展開し、 $U + V + W = 1 - (X + Y + Z)$ を使って整理すると次の式が得られます。

$- e^{i π (V + W - U)} + e^{- i π (V + W - U)} - e^{i π (W + U - V)} + e^{- i π (W + U - V)} - e^{i π (U + V - W)} + e^{- i π (U + V - W)} = - e^{i π (Y + Z - X)} + e^{- i π (Y + Z - X)} - e^{i π (Z + X - Y)} + e^{- i π (Z + X - Y)} - e^{i π (X + Y - Z)} + e^{- i π (X + Y - Z)}$

すべての項を左辺に移動し、マイナス記号を $e^{- i π}$ に変換し、 $i = e^{i π / 2}$ を掛けて、

$α_{1} = V + W - U - 1 / 2$
$α_{2} = W + U - V - 1 / 2$
$α_{3} = U + V - W - 1 / 2$
$α_{4} = Y + Z - X + 1 / 2$
$α_{5} = Z + X - Y + 1 / 2$
$α_{6} = X + Y - Z + 1 / 2$

としてみると、このようになります。

$\sum_{j = 1}^{6} e^{i π α_{j}} + \sum_{j = 1}^{6} e^{- i π α_{j}} = 0$

このとき
$\sum_{j = 1}^{6} α_{j} = U + V + W + X + Y + Z = 1$
です。

逆に、和が $1$ になり上式を満たす有理数 $α_{1}, α_{2}, α_{3}, α_{4}, α_{5}, α_{6}$ （必ずしも正ではない）があれば、 $U, V, W, X, Y, Z$ が復元できます（例えば、 $U ＝（ α_{2} ＋ α_{3} ） / 2 ＋ 1 / 2$ のように）。
ただし、この場合、解が正になることを確認する必要があります。

さらに一般化して考える

論文では、さらに一般化して

$\sum_{i = 1}^{k} a_{i} η_{i} = 0$

のような関係を考察していきます。
ここで、 $a_{i}$ は正の整数で、 $η_{i}$ は相異なる１の冪根です。
このような関係を満たすパターンは有限で、円分多項式やガロア群を使って分類できるようです。ここから先の論文の内容は私の理解を超えていますので、どなたか論文を読み解いていただけるとうれしいです。

おまけ(チェバの定理との関係)

ところで、この式の形がいわゆるチェバの定理と同じ形であることにお気づきでしょうか。

$\frac{A F}{F B} \cdot \frac{B D}{D C} \cdot \frac{C E}{E A} = 1$

弦バージョンのチェバの定理 AF/FB・BD/DC・CE/EA=1

普通のチェバの定理 AF/FB・BD/DC・CE/EA=1

実際、チェバの定理と密接な関係があります。

そのことに関して、偶然みつけたこちらのPDFに興味深い記事がありました。なかなか面白いと思いますのでご紹介します。

PDFファイル

おわりに

とりあえず、現時点でわかっている範囲の情報をまとめたつもりです。

足りない部分も多々あると思いますが、適宜フォローしていただけるとありがたいと思います。

最後に、記事中の式などを含むDesmosファイルを置いておきますので、いろいろ遊んでみてください。

Desmosファイル

参考文献

[1]

Bjorn Poonen, Michael Rubinstein, (arxiv)The Number of Intersection Points Made by the Diagonals of a Regular Polygon, 閲覧日 2022年2月5日, https://arxiv.org/abs/math/9508209

[2]

数学研究-正18角形の対角線-, 閲覧日 2022年2月5日, https://tomodak.com/report/#18

投稿日：2022年2月5日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

apu_yokai

488

66818

他の人のコメント

コメントはありません。

読み込み中

apu_yokai

正多角形の対角線の交点の数について(GIFあり)

はじめに
論文の紹介
きっかけのツイート
交点の数の上限
正多角形の対角線の交点の数の上限は二項係数でわかる
正多角形の対角線の交点の数の公式
公式を分解する
正 $30$ 角形は特別
対角線で分割される領域数を数える
論文での証明のアイデア
$3$ 本の対角線が共点となる条件
三角関数版ディオファントス方程式
複素数の不定方程式を作る
さらに一般化して考える
おまけ(チェバの定理との関係)
おわりに
参考文献

正多角形の対角線の交点の数について(GIFあり)

はじめに

論文の紹介

きっかけのツイート

交点の数の上限

正多角形の対角線の交点の数の上限は二項係数でわかる

正多角形の対角線の交点の数の公式

公式を分解する

正30角形は特別

対角線で分割される領域数を数える

領域の数を数えるもう一つの方法

論文での証明のアイデア

3本の対角線が共点となる条件

三角関数版ディオファントス方程式

複素数の不定方程式を作る

さらに一般化して考える

おまけ(チェバの定理との関係)

おわりに

参考文献

この記事を高評価した人

この記事に送られたバッジ

投稿者

コメント

他の人のコメント

正 $30$ 角形は特別

$3$ 本の対角線が共点となる条件