高校数学解説

三角形の内接円と外接円の相似比

三角関数,初等幾何,高校数学

251

これは Math Advent Calendar 2024 の $1$ 日目の記事です。

この記事は、「三角形の内接円と外接円の相似比の明示公式とその例・応用について述べるもの」です。
内容のレベルは高校数学で、ジャンルは初等幾何学です。

平面において、三角形に対し内接円・外接円と呼ばれる $2$ つの円を見出すことができるのでした。これは、それぞれ次のように定義されるものです。

（内心の存在）

三角形の各角の二等分線は一点で交わる。この交点のことをもとの三角形の内心と呼ぶ。

（内接円）

内心を中心として三角形のある辺（どの辺でもよい）までの距離を半径とした円を書くと、これはその三角形の全ての辺に接する。

こうして作った円をもとの三角形の内接円と呼ぶ。

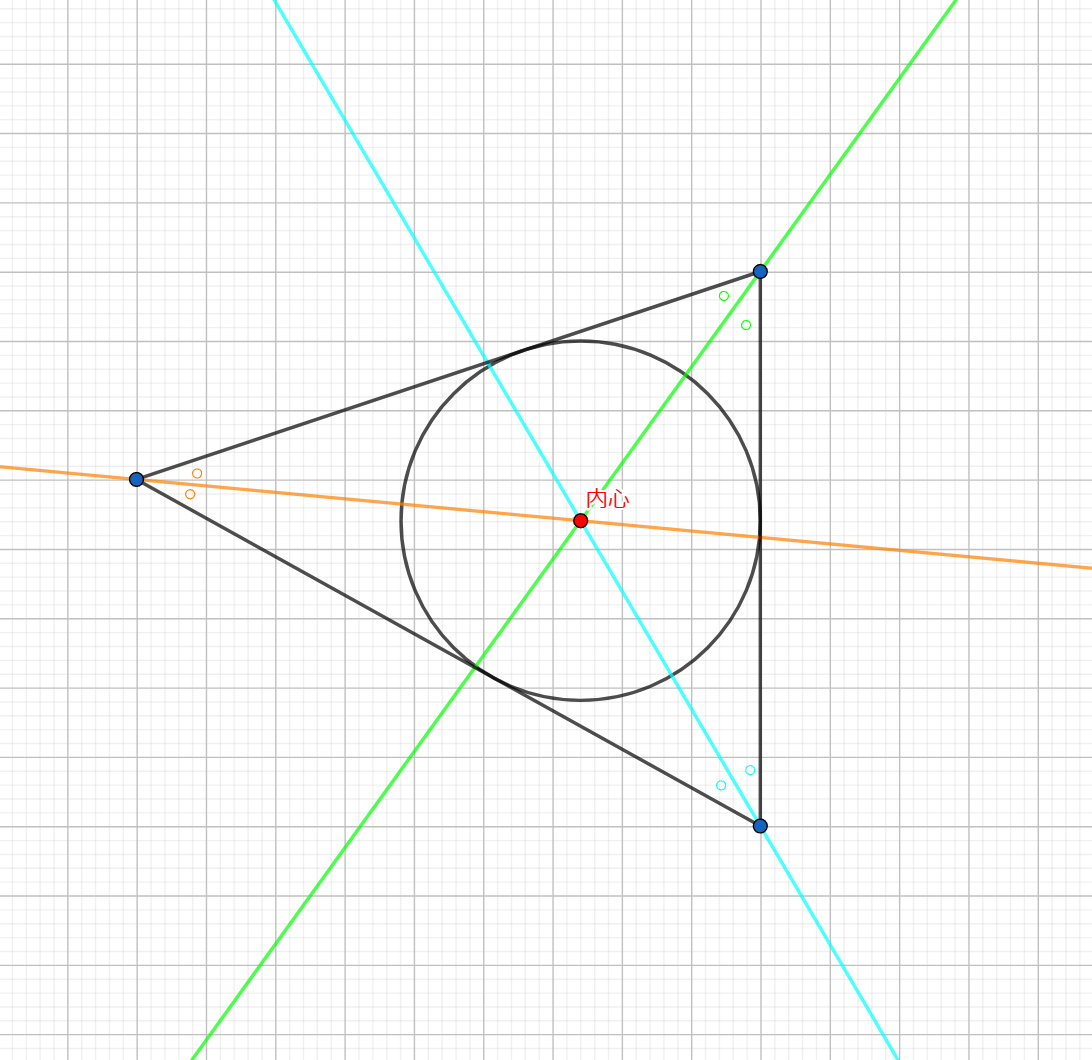内接円

（外心の存在）

三角形の各辺の垂直二等分線は一点で交わる。この交点のことをもとの三角形の外心と呼ぶ。

（外接円）

外心を中心として三角形のある頂点（どの頂点でもよい）までの距離を半径とした円を書くと、これはその三角形の全ての頂点を通る。

こうして作った円をもとの三角形の外接円と呼ぶ。

外接円

さて、円という図形は全て相似であり、その相似比は各々の半径の比です。それでは、この「内接円と外接円の相似比」はどれくらいなのでしょうか？これら $2$ つの円の大きさの違いを、元になった三角形の情報から記述できるのでしょうか？

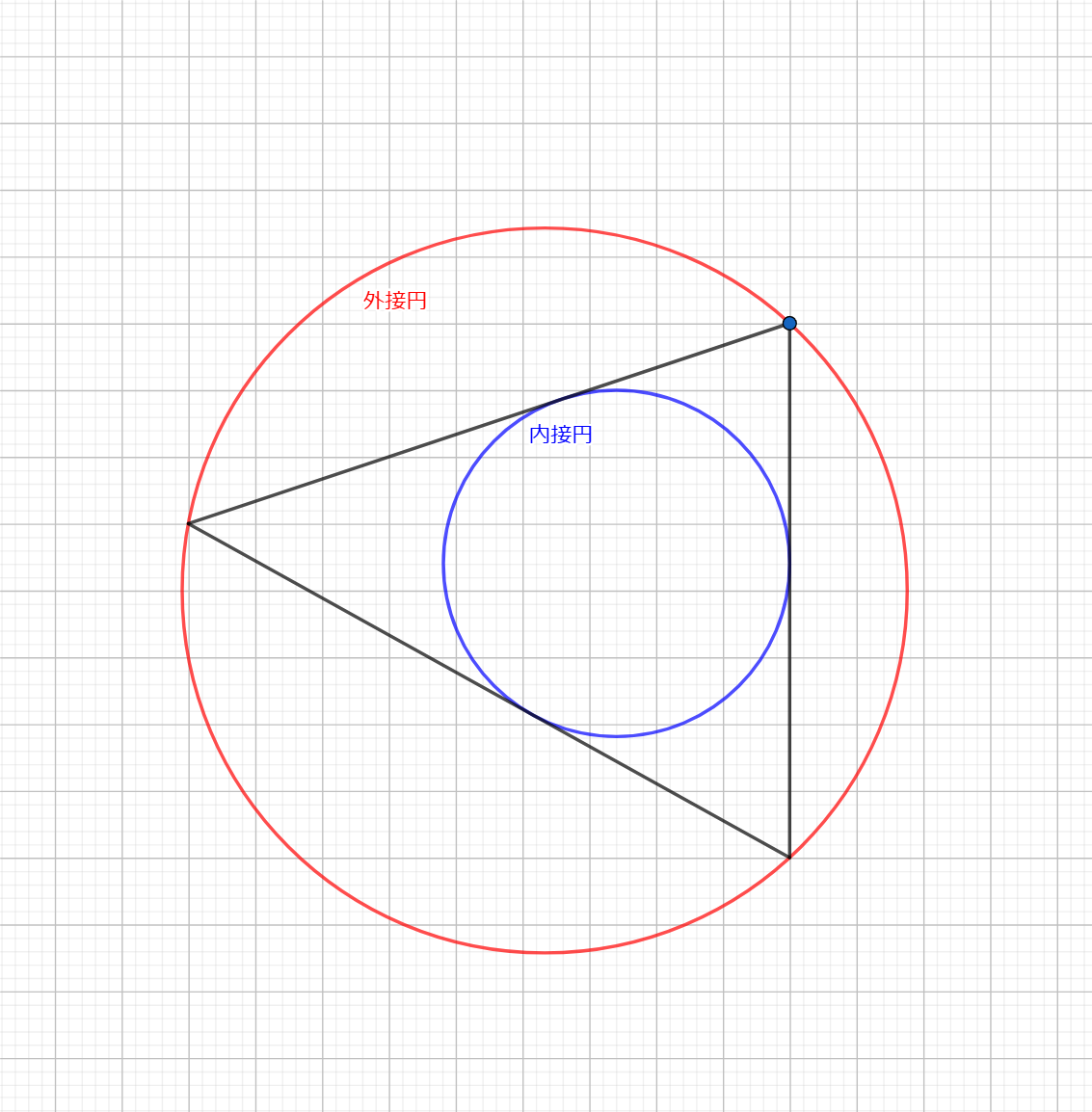三角形の内接円と外接円

今回の記事では、それが実際に可能であり、「三角形の外接円の半径に対する内接円の半径の比を、三角形の角度の情報を用いて表示できる」ことを紹介・証明します。関連して、その結果から得られるいくつかの系も記載します。

最後に、三角形の表示に関する注意を述べます。
本記事において、三角形の $3$ つの角をそれぞれ $A, B, C$ で表します。また、それぞれの角に向かい合う辺を $a, b, c$ で表します。
即ち、三角形の角と辺が以下の画像のような位置関係であることを念頭に置いて命題・証明・例の記述を行うことに注意します。

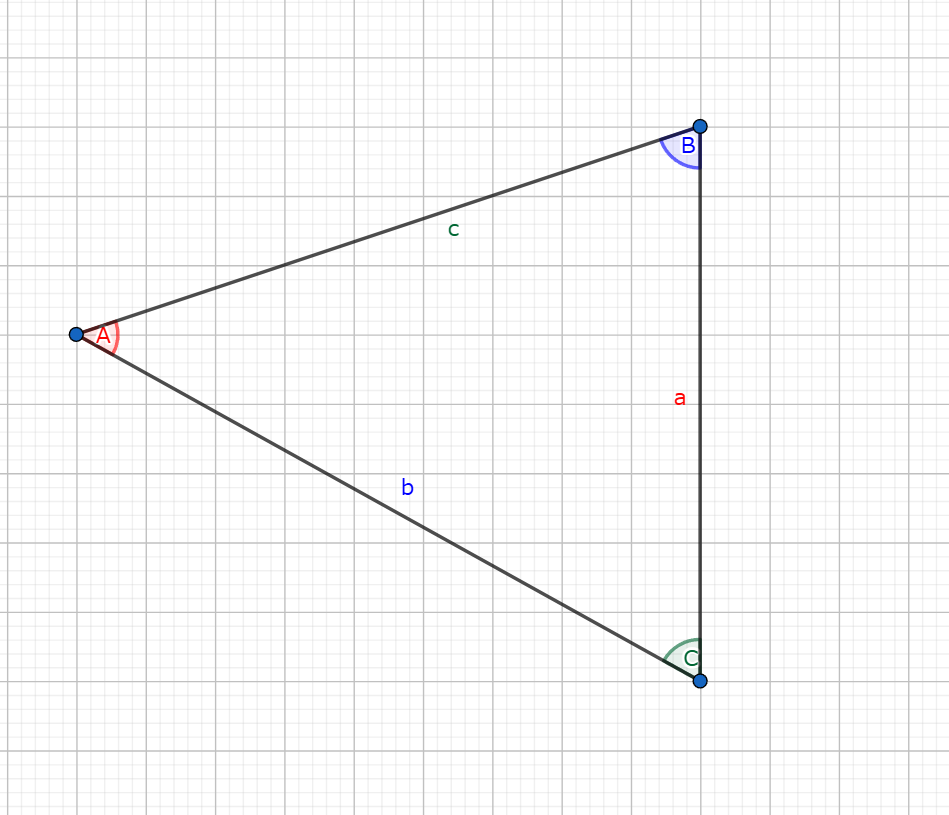位置関係

主定理とその例

主張を述べるにあたって、初めに $1$ つ定義を行います。

（

β

定数）

内角が $A, B, C$ である三角形について、定数 $β$ （あるいはより詳しく $β (A, B, C)$ ）を

$β = \cos A + \cos B + \cos C$

と定義する

「 $β$ 定数」という呼び名は独自のものであり、一般的なものではないことに注意します。

（

β

定数の計算例）

正三角形の $β$ 定数の値は $\cos \frac{π}{3} + \cos \frac{π}{3} + \cos \frac{π}{3} = \frac{1}{2} + \frac{1}{2} + \frac{1}{2} = \frac{3}{2}$ である。

また、直角二等辺三角形の $β$ 定数の値は $\cos \frac{π}{4} + \cos \frac{π}{4} + \cos \frac{π}{2} = \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} + 0 = \sqrt{2}$ である。

さらに、辺の長さが $3, 4, 5$ である直角三角形の $β$ 定数の値は $\frac{3}{5} + \frac{4}{5} + 0 = \frac{7}{5}$ である。

!FORMULA[21][36213][0] つ目の三角形 $3$ つ目の三角形

この $β$ 定数を用いて内接円と外接円の相似比を次のように表示することができます。

（主定理：内接円と外接円の相似比）

三角形の外接円に対する内接円の相似比は $β$ 定数を用いて $1 : β - 1$ と表される。

即ち、三角形の外接円の半径及び内接の半径をそれぞれ $R, r$ とすると、 $R (β - 1) = r$ が成り立つ。

この記事ではこの定理（のみ）を主定理と呼び、以下のいくつかの箇所で参照します。

以下、この定理の主張を具体例とともに観察してみようと思います。

（色々な三角形の内接円・外接円の相似比）

正三角形の $β$ 定数の値は $\frac{3}{2}$ であった。したがって、外接円に対する内接円の相似比は $1 : \frac{3}{2} - 1 = 2 : 1$ 。即ち、外接円の大きさは内接円の $2$ 倍である。

直角二等辺三角形の $β$ 定数の値は $\sqrt{2}$ であった。したがって、外接円に対する内接円の相似比は $1 : \sqrt{2} - 1 = \sqrt{2} + 1 : 1$ 。即ち、外接円の大きさは内接円の $\sqrt{2} + 1 \approx 2.4$ 倍である。

辺の長さが $3, 4, 5$ である直角三角形の $β$ 定数の値は $\frac{7}{5}$ であった。したがって、外接円に対する内接円の相似比は $1 : \frac{7}{5} - 1 = 2.5 : 1$ 。即ち、外接円の大きさは内接円の $2.5$ 倍である。

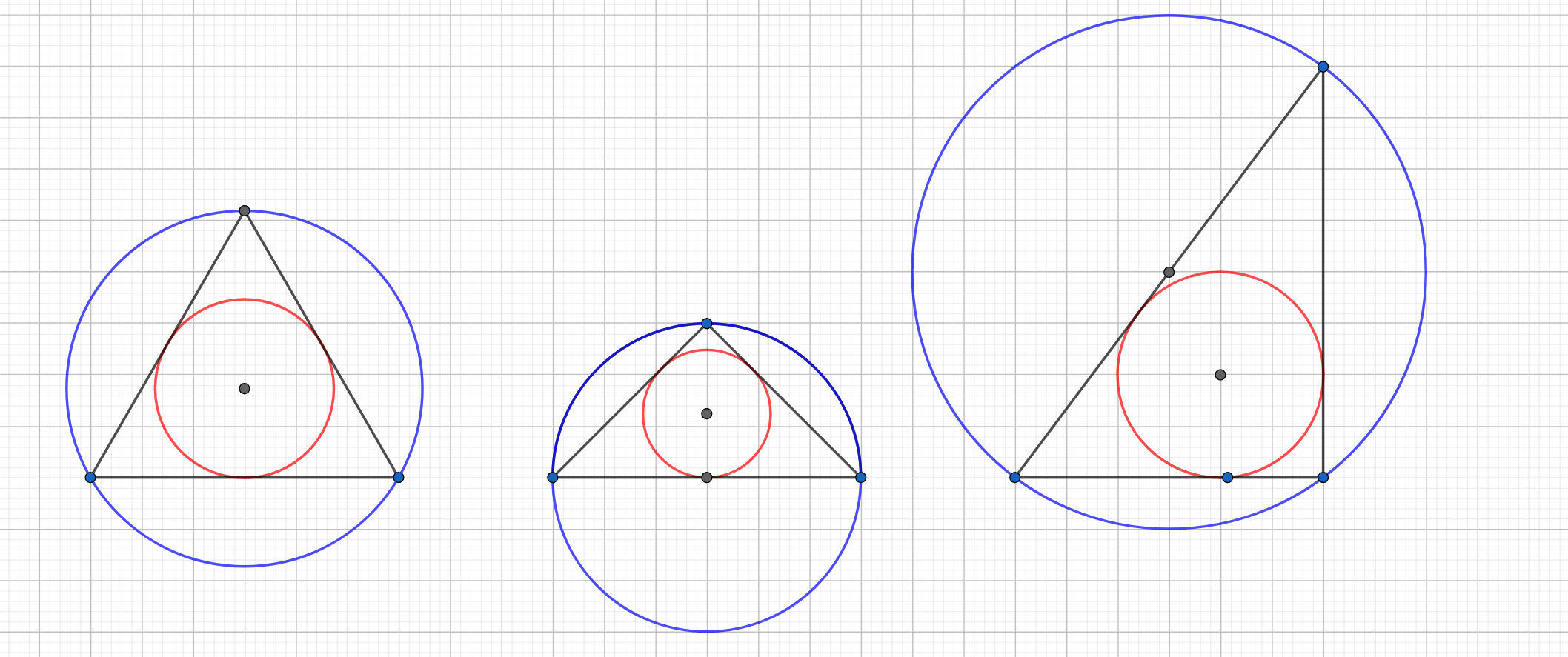色々な三角形の内接円と外接円

ラフな説明にはなりますが、こう見てみると、主に三角形の潰れ具合によって内接円の半径が小さくなり、それが結果として $β$ 定数の値に影響していることがわかります。
三角形の潰れ具合が最も小さい「正三角形」の内接円はこの $3$ つの中で最も大きく、故に外接円に対する比の値を（よって $β$ 定数の値を）最も大きくします。
また、三角形の潰れ具合が最も大きい「辺の長さが $3, 4, 5$ である直角三角形」の内接円はこの $3$ つの中で最も小さく、故に外接円に対する比の値を（よって $β$ 定数の値を）最も小さくします。
（むしろ $β$ 定数の値を「三角形の潰れ具合の指標」とみなすべきなのかもしれません。）

さらに、この相似比計算には角度の情報しか利用していません。
よって「相似な三角形はすべて共通の『外接円に対する内接円の比の値』を持つ」ことがわかります。

主定理の証明

以下、この主定理の証明のため、いくつか補題を用意します。
ただし、その中で高校数学においてあまりにも使われている公式や、「～の公式」というように名称が既にあるものについては、その検索可能性から証明を省略しようと思います。

また、改めて三角形の辺・角の位置関係が次のようであることを再掲しておきます。

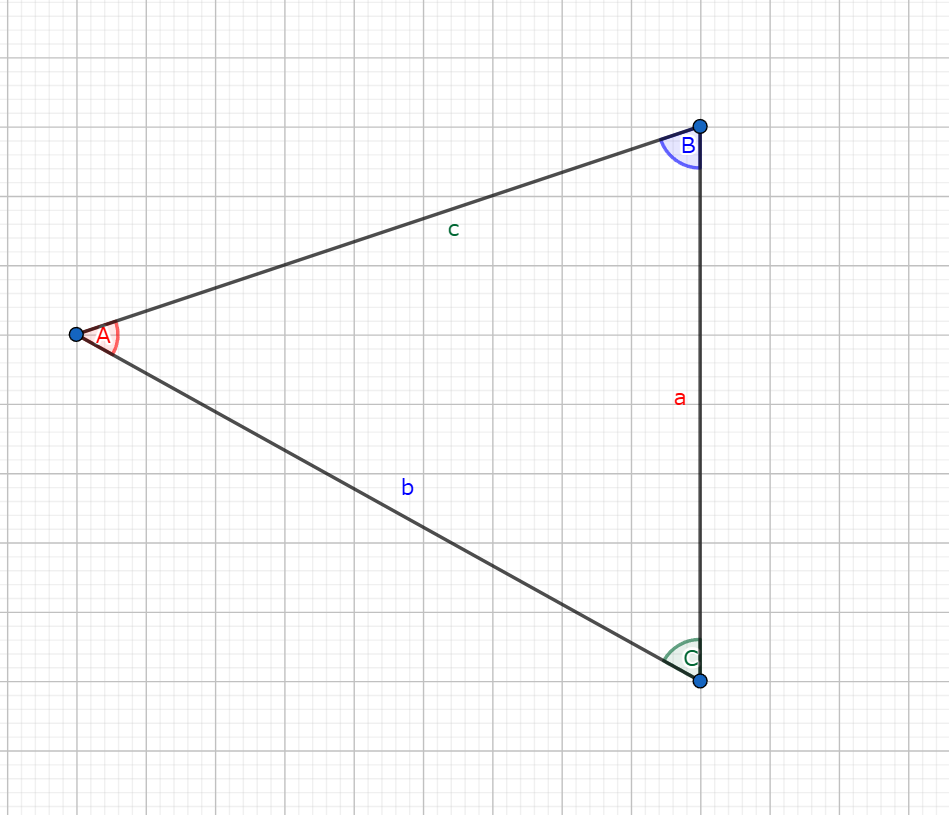辺と角の位置関係

（正弦定理）

三角形の三辺 $a, b, c$ 及び対応する三角 $A, B, C$ , そしてその外接円の半径 $R$ の間に次の関係式が成り立つ。

$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2 R$

（余弦定理）

三角形の三辺 $a, b, c$ 及び対応する三角 $A, B, C$ の間に次の関係式が成り立つ。

$a^{2} = b^{2} + c^{2} - 2 b c \cos A$
$b^{2} = c^{2} + a^{2} - 2 c a \cos B$
$c^{2} = a^{2} + b^{2} - 2 a b \cos C$

（

2

辺とその間の角による面積公式）

三角形の三辺 $a, b, c$ 及び対応する三角 $A, B, C$ を用いて、三角形の面積 $S$ は以下のようにあらわされる。

$S = \frac{1}{2} b c \sin A = \frac{1}{2} c a \sin B = \frac{1}{2} a b \sin C$

（ヘロンの公式）

三角形の三辺を $a, b, c$ とし、 $t := \frac{1}{2} (a + b + c)$ とおく。このとき、この三角形の面積 $S$ は以下のようにあらわされる。

$S = \sqrt{t (t - a) (t - b) (t - c)}$

（内接円の半径による面積公式）

三角形の三辺を $a, b, c$ 、その内接円の半径を $r$ とする。 $t := \frac{1}{2} (a + b + c)$ とおく。このとき、この三角形の面積 $S$ は以下のようにあらわされる。

$S = t r$

下記画像のように、三角形を「その内心 $I$ から伸びる各辺への線分」で分割する。

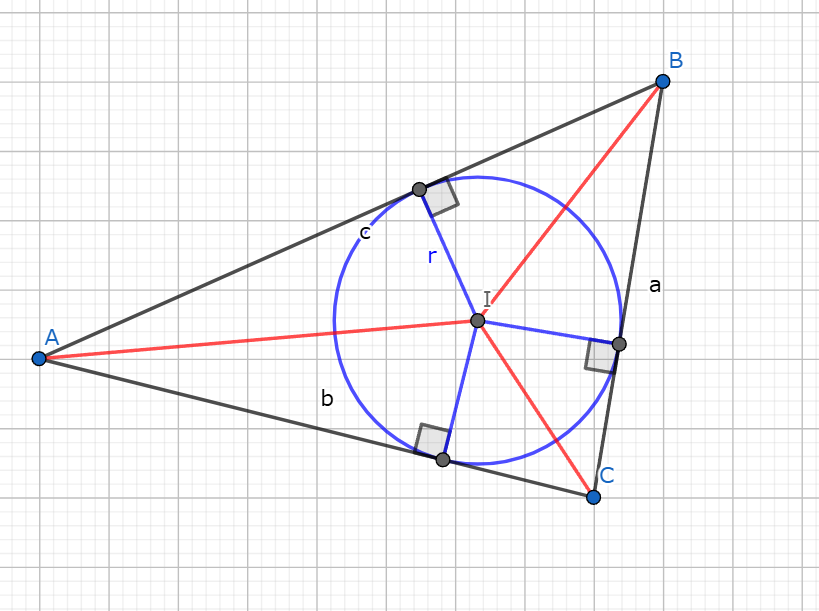内接円の半径と面積

すると、 $S = \frac{1}{2} a r + \frac{1}{2} b r + \frac{1}{2} c r = t r$ である。

（外接円の半径による面積公式）

三角形の三辺を $a, b, c$ 、その外接円の半径を $R$ とする。このとき、次の関係式が成り立つ。

$a b c = 4 S R$

正弦定理及び「 $2$ 辺とその間の角による面積公式」から、 $S = \frac{1}{2} b c \sin A = \frac{1}{2} b c \cdot \frac{a}{2 R} = \frac{a b c}{4 R}$ である。これを整理して主張を得る。

以下、主定理の証明をします。

（主定理の証明）

余弦定理を用いて、次のように変形していく。

$\begin{aligned} β - 1 & = \cos A + \cos B + \cos C - 1 \\ = \frac{b^{2} + c^{2} - a^{2}}{2 b c} + \frac{c^{2} + a^{2} - b^{2}}{2 c a} + \frac{a^{2} + b^{2} - c^{2}}{2 a b} - 1 \\ = \frac{1}{2 a b c} {a (b^{2} + c^{2} - a^{2}) + b (c^{2} + a^{2} - b^{2}) + c (a^{2} + b^{2} - c^{2}) - 2 a b c} \\ = \frac{1}{2 a b c} (a b^{2} + c^{2} a - a^{3} + b c^{2} + a^{2} b - b^{3} + c a^{2} + b^{2} c - c^{3} - 2 a b c) \\ = \frac{1}{2 a b c} {- a^{3} + (b + c) a^{2} + (b^{2} - 2 b c + c^{2}) a + (- b^{3} + b c^{2} + b^{2} c - c^{3})} \\ = \frac{1}{2 a b c} {- a^{3} + (b + c) a^{2} + (b - c)^{2} a + (- b (b^{2} - c^{2}) + (b^{2} - c^{2}) c)} \\ = \frac{1}{2 a b c} {(b + c - a) a^{2} + (b - c)^{2} a - (b - c)^{2} (b + c)} \\ = \frac{1}{2 a b c} (b + c - a) {a^{2} - (b - c)^{2}} \\ = \frac{1}{2 a b c} (b + c - a) (a - b + c) (a + b - c) \end{aligned}$

ここで、 $t = \frac{1}{2} (a + b + c)$ とおく。また $S$ を三角形の面積とする。その上で、ヘロンの公式と「内接円の半径による面積公式」を用いれば、

$\begin{aligned} β - 1 & = \frac{1}{2 a b c} \cdot 2 (t - a) \cdot 2 (t - b) \cdot 2 (t - c) \\ = \frac{4}{a b c t} t (t - a) (t - b) (t - c) \\ = \frac{4}{a b c t} S^{2} \\ = \frac{4}{a b c t} S \cdot t r \\ = \frac{4 S r}{a b c} \end{aligned}$

を得る。最後に、「外接円の半径による面積公式」を用いれば、下記のように主張を得る。

$β - 1 = \frac{4 S r}{a b c} = \frac{4 S r}{4 S R} = \frac{r}{R}$

特別な三角形に対する系

ここまでで、一般的な三角形において外接円と内接円の大きさの比を導出してきました。
ここで、その結果の系として、「特徴的な三角形についてはその比がどのようにして計算できるのか」を見てみようと思います。
取り扱うのは、「正三角形」「二等辺三角形」「直角三角形」の $3$ つです。

まず、正三角形の場合の系を明示します。上で記載した内容と重複するのですが、この場合 $β$ 定数が $\frac{3}{2}$ になるので、次の結果が得られます。

（正三角形の場合の相似比）

正三角形において、外接円と内接円の相似比は $2 : 1$ である。
即ち、正三角形の外接円の半径 $R$ と内接円の半径 $r$ について、 $R = 2 r$ が成り立つ。

次に二等辺三角形の場合の系を見てみます。
この場合、 $β$ 定数を「角度を用いて計算する」か「辺を用いて計算するか」によって異なる形の結果が得られます。最初に、「角度を用いて計算した結果」を確認してみます。

下記画像のように底角を $θ$ として考えてみます。
底角を !FORMULA[91][1782773758][0] とする二等辺三角形底角を $θ$ とする二等辺三角形

（底角を設定した場合の相似比）

底角を $θ$ とした二等辺三角形を考える。
このとき、この二等辺三角形の外接円と内接円の相似比は $1 : β - 1 = 1 : 2 \cos θ (1 - \cos θ) = 1 : {\frac{1}{2} - 2 (\cos θ - \frac{1}{2})^{2}}$ である。

即ち、二等辺三角形の外接円の半径 $R$ と内接円の半径 $r$ について、 $R (β - 1) = 2 \cos θ (1 - \cos θ) R ＝ {\frac{1}{2} - 2 (\cos θ - \frac{1}{2})^{2}} R = r$ が成り立つ。

主張において、 $β - 1 = 2 \cos θ (1 - \cos θ)$ を示せば、残りの部分は $\cos θ$ に関する平方完成によって得られる。
そしてこれは倍角の公式を用いた次の計算によりわかる。

$\begin{aligned} β - 1 & = \cos θ + \cos θ + \cos (π - 2 θ) - 1 \\ = 2 \cos θ - \cos (2 θ) - 1 \\ = 2 \cos θ - (2 \cos^{2} θ - 1) - 1 \\ = 2 \cos θ (1 - \cos θ) \end{aligned}$

このことからわかるのは、二等辺三角形の外接円と内接円の相似比は、正三角形の場合（ $\cos θ = \frac{1}{2}$ 即ち $θ = \frac{π}{6}$ ）の場合を頂点として、ちょうど二次関数的に変遷するということです。このことは、直感的にも「二等辺三角形の山があまりにも低くなったり高くなったりしすぎると、内接円が小さくなり、相似比は小さくなりそう」だと考えられます。そして、その「潰れ具合」のバランスが最も良いときが正三角形であり、その時内接円が（よって相似比が）最大値である「外接円の長さの $\frac{1}{2}$ 」をとるのだ、と思うことができるのです。

次に、「辺を用いて計算した結果」を確認してみます。
下記画像のような設定で考えてみます。

斜辺が !FORMULA[103][37639][0] で底辺が !FORMULA[104][37670][0] の二等辺三角形斜辺が $a$ で底辺が $b$ の二等辺三角形

（各辺の長さを設定した場合の相似比）

斜辺が $a$ で底辺が $b$ の二等辺三角形を考える。
このとき、この二等辺三角形の外接円と内接円の相似比は $1 : β - 1 = 1 : \frac{b}{2 a^{2}} (2 a - b)$ である。

即ち、二等辺三角形の外接円の半径 $R$ と内接円の半径 $r$ について、 $R (β - 1) = \frac{b}{2 a^{2}} (2 a - b) R ＝ r$ が成り立つ。

二等辺三角形の底角の大きさを $θ$ とする。このとき、 $\cos θ = \frac{\frac{b}{2}}{a} = \frac{b}{2 a}$ である。
よって一つ前の命題にこれを代入すれば $β - 1 = 2 \cos θ (1 - \cos θ) = 2 \cdot \frac{b}{2 a} \cdot (1 - \frac{b}{2 a}) = \frac{b}{2 a^{2}} (2 a - b)$ となり主張が従う。

この場合は、ちょっとした表示式が得られることになりました。

最後に、直角三角形の場合の系を見てみます。
下記画像のような設定で考えてみます。

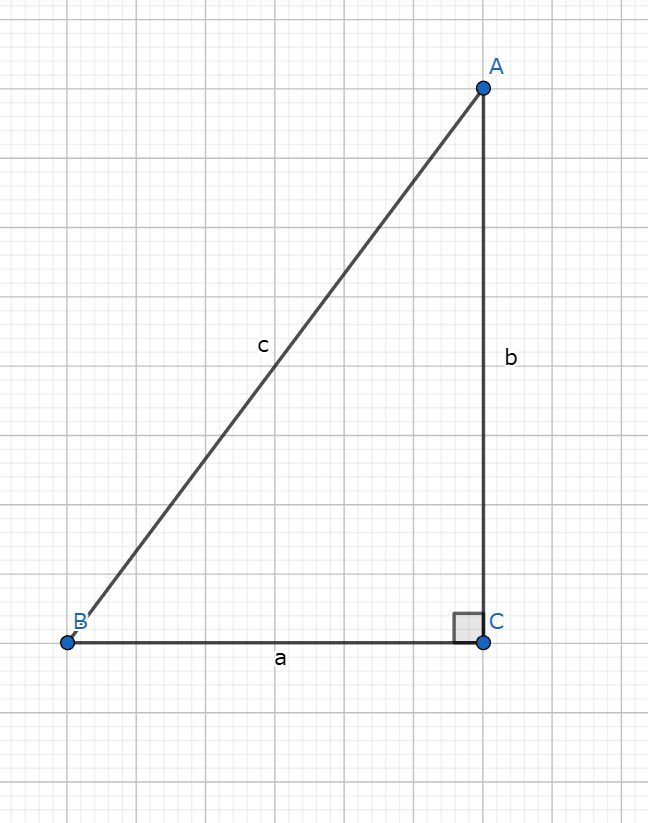直角三角形

（直角三角形の場合の相似比）

底辺が $a, b$ で斜辺が $c$ の直角三角形を考える。
このとき、この二等辺三角形の外接円と内接円の相似比は $1 : β - 1 = 1 : \frac{a + b - c}{c}$ である。

即ち、二等辺三角形の外接円の半径 $R$ と内接円の半径 $r$ について、 $R (β - 1) = \frac{a + b - c}{c} R ＝ r$ が成り立つ。

$β - 1 = \cos A + \cos B + \cos C - 1 = \frac{b}{c} + \frac{a}{c} + 0 - 1 = \frac{a + b - c}{c}$ より主張を得る。

実は、この関係式から直角三角形の内接円の半径の表示について下記の事実がわかります。

(直角三角形の内接円の半径)

底辺が $a, b$ で斜辺が c の直角三角形を考える。このとき、この直角三角形の内接円の半径 $r$ は次のように書ける。
$r = \frac{1}{2} (a + b - c)$

例えば、底辺・高さ・斜辺が $3, 4, 5$ である直角三角形の場合は内接円の半径は $\frac{1}{2} (3 + 4 - 5) = 1$ になりますし、 $5, 12, 13$ の場合は $\frac{1}{2} (5 + 12 - 13) = 2$ になります。

直角三角形において、その斜辺の長さは外接円の直径に一致することに注意する（この事実の証明は、本質的には円周角の定理だが、おそらく正弦定理で「斜辺に向かい合う角が直角である」ことに気づく方が早い。）。

よって、この直角三角形の外接円の半径 $R$ について、 $c = 2 R$ である。これと直前の結果である $\frac{a + b - c}{c} R ＝ r$ を合わせれば次のようにして主張を得る。

$r = \frac{a + b - c}{c} R = \frac{a + b - c}{2 R} R ＝ \frac{1}{2} (a + b - c)$

$β$ 定数の存在範囲

さて、ここまで $β$ 定数の表示をいろいろな三角形についてみてきました。
次は、「この $β$ という定数はどのような存在範囲をもつのか？」について考えてみたいと思います。

即ち、次の条件を満たすような実数の区間 $I$ を特定します。

いかなる三角形についても、その三角形の $β$ 定数の値は $I$ に属する。
$I$ に属する勝手な値について、 $β$ 定数の値がその値になるような三角形が存在する。

前者については、ごく簡単には次のように評価できます。

（

β

定数の自明な評価）

$β$ 定数は $1 < β \leq 3$ を満たす。

主定理より、 $β = \frac{r}{R} + 1 > 1$ である。
また、 $β$ 定数の定義から $β = \cos A + \cos B + \cos C \leq 1 + 1 + 1 = 3$ である。

しかしながら、これは少しラフな評価です。 $β - 1 = \frac{r}{R}$ であることを思い出すと、 $β$ はおおよそ「外接円に対する内接円の比」、もう少し言うと「三角形の潰れ具合」を表していると思えたのでした（ $β$ の値が小さいほどより潰れている）。

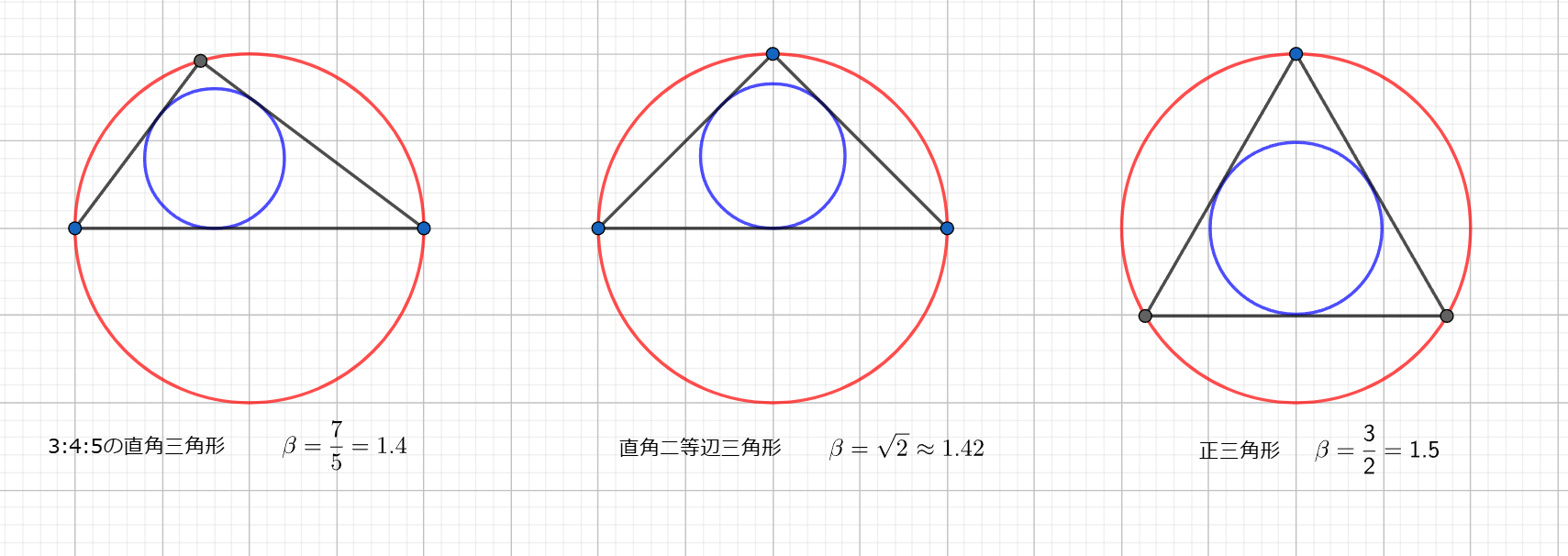異なる三角形における比較（外接円の大きさは同じ）

この点から考えると、三角形の「潰れ（ $β$ ）」は「下界である $1$ まではどこまでも小さくできる。一方で、これは正三角形の $\frac{3}{2}$ で最大となるだろう」と思えます。
即ち、一つ前の自明な評価について上界を $\frac{3}{2}$ に改善でき、しかもこれが最大値であることが予想できます。
以下、この予想を証明します。

（

β

定数の精密な評価）

$β$ 定数は $1 < β \leq \frac{3}{2}$ を満たす。

$1 < β$ は既にわかっているから $β \leq \frac{3}{2}$ を示せば良い。また、 $β = \frac{3}{2}$ となる三角形の存在は、正三角形によって既にわかっていることに注意する。

さて、 $β \leq \frac{3}{2}$ は三角形の三辺 $a, b, c$ に関する不等式

$a b^{2} + c^{2} a + b c^{2} + a^{2} b + c a^{2} + b^{2} c \leq a^{3} + b^{3} + c^{3} + 3 a b c$

を示すことで従う。実際、この不等式が示せていたとすると、
$\begin{aligned} a b^{2} + c^{2} a + b c^{2} + a^{2} b + c a^{2} + b^{2} c & \leq a^{3} + b^{3} + c^{3} + 3 a b c \\ (a b^{2} + c^{2} a - a^{3}) + (b c^{2} + a^{2} b - b^{3}) + (b^{2} c + c a^{2} - c^{3}) & \leq 3 a b c \\ a (b^{2} + c^{2} - a^{2}) + b (c^{2} + a^{2} - b^{2}) + c (b^{2} + a^{2} - c^{2}) & \leq 3 a b c \\ \frac{a (b^{2} + c^{2} - a^{2})}{2 a b c} + \frac{b (c^{2} + a^{2} - b^{2})}{2 a b c} + \frac{c (b^{2} + a^{2} - c^{2})}{2 a b c} & \leq \frac{3}{2} \\ \frac{b^{2} + c^{2} - a^{2}}{2 b c} + \frac{c^{2} + a^{2} - b^{2}}{2 c a} + \frac{b^{2} + a^{2} - c^{2}}{2 a b} & \leq \frac{3}{2} \end{aligned}$

最後に余弦定理を用いて左辺の各項を書きかえれば主張が従う。

下記の不等式を示す。右辺から左辺を引いた結果が非負であることを示す。辺の対称性から $a \leq b \leq c$ と仮定してよい。
$a b^{2} + c^{2} a + b c^{2} + a^{2} b + c a^{2} + b^{2} c \leq a^{3} + b^{3} + c^{3} + 3 a b c$

$\begin{aligned} a^{3} + b^{3} + c^{3} + 3 a b c - (a b^{2} + c^{2} a + b c^{2} + a^{2} b + c a^{2} + b^{2} c) & = (a^{3} + a^{2} b - a b^{2} - b^{3}) + c^{3} + 3 a b c - c^{2} a - b c^{2} - c a^{2} - b^{2} c \\ = (a + b) (a - b)^{2} + (c^{3} - c^{2} a) - (b c^{2} - a b c) + (a b c - c a^{2}) - (b^{2} c - a b c) \\ = (a + b) (b - a)^{2} + c^{2} (c - a) - b c (c - a) + c a (b - a) - b c (b - a) \\ = (a + b) (b - a)^{2} + c (c - a) (c - b) - c (b - a)^{2} \\ = (a + b - c) (b - a)^{2} + c (c - a) (c - b) \geq 0 \end{aligned}$

となり、不等式が証明できた。なお、最終行の第一項は三角形の三辺の関係式 $a + b > c$ により正である。

余談ですが、 $β \leq \frac{3}{2}$ の別証明として、「ラグランジュの未定乗数法」という強力なアイテムを使う別証明があります。
ここではそれを詳解することはしませんが、「関数 $f (x, y, z) = \cos (x) + \cos (y) + \cos (z)$ について、境界条件 $x + y + z = π$ の下で極大値（最大値）を求める」ことで目標である $β \leq \frac{3}{2}$ を得ることができます。

さて、ここまでで、目標の半分ができました。即ち $I = (1, \frac{3}{2}]$ として、下記の前半が言えています。

次のような実数の区間 $I$ を特定する。

いかなる三角形についても、その三角形の $β$ 定数の値は $I$ に属する。
$I$ に属する勝手な値について、 $β$ 定数の値がその値になるような三角形が存在する。

後半を証明します。
三角形一般について証明するのは大変ですが、幸いにも前節で証明の足掛かりになる結果を一つ確認しています。

（二等辺三角形の

β

定数）

底角が $θ$ である二等辺三角形（よって $3$ つの角は $θ, θ, π - 2 θ$ ）について、下記が成り立つ。

$β - 1 = 2 \cos θ (1 - \cos θ) = \frac{1}{2} - 2 (\cos θ - \frac{1}{2})^{2}$

これを用いれば、パラメータ $θ$ をいろいろに動かすことでうまく後半を証明できるのではないでしょうか？
即ち、以下が成り立ちそうに思えます。

勝手な $c \in (1, \frac{3}{2}]$ について、 $β$ 定数の値がその値になるような二等辺三角形が存在する。

即ち、勝手な $c \in (1, \frac{3}{2}]$ について、適当な $θ \in (0, \frac{π}{2})$ が存在して、 $β (θ, θ, π - 2 θ) = c$ が成り立つ。

より簡単な証明のために、パラメータをいろいろと動かして、できる限り簡単な形に主張を帰着してみましょう。
$c = \frac{3}{2}$ のときに主張が成り立つことは正三角形の存在からわかっているので、 $c$ の範囲を $c \in (1, \frac{3}{2})$ に狭めて議論します。

勝手な $c \in (1, \frac{3}{2})$ について、適当な $θ \in (0, \frac{π}{2})$ が存在して、 $β (θ, θ, π - 2 θ) = c$ が成り立つ。

$\Leftrightarrow$ 勝手な $c \in (0, \frac{1}{2})$ について、適当な $θ \in (0, \frac{π}{2})$ が存在して、 $β (θ, θ, π - 2 θ) - 1 = \frac{1}{2} - 2 (\cos θ - \frac{1}{2})^{2} = c$ が成り立つ。

$\Leftrightarrow$ 勝手な $c \in (0, \frac{1}{2})$ について、適当な $θ \in (0, \frac{π}{2})$ が存在して、 $2 (\cos θ - \frac{1}{2})^{2} = c$ が成り立つ。

$\Leftrightarrow$ 勝手な $c \in (0, \frac{1}{4})$ について、適当な $θ \in (0, \frac{π}{2})$ が存在して、 $(\cos θ - \frac{1}{2})^{2} = c$ が成り立つ。

$\Leftarrow$ 勝手な $c \in (0, \frac{1}{2})$ について、適当な $θ \in (0, \frac{π}{2})$ が存在して、 $\cos θ - \frac{1}{2} = c$ が成り立つ。

$\Leftrightarrow$ 勝手な $c \in (\frac{1}{2}, 1)$ について、適当な $θ \in (0, \frac{π}{2})$ が存在して、 $\cos θ = c$ が成り立つ。

最終的に、かなり単純な形に主張を帰着することができました。ところが、最終行に書かれた命題は $\cos$ の連続性から明らかです。
従って、目標の後半部分も正しいと確認できたことになります。

最後に、ここで得られた結果を主定理に応用して、結果を $1$ つ得たいと思います。この結果には「オイラーの不等式」という名前がついているようです。

（オイラーの不等式）

三角形の外接円の半径 $R$ 及び内接円の半径 $r$ の間に次の関係が成り立つ。

$2 r \leq R$

$\frac{r}{R} = β - 1 \leq \frac{3}{2} - 1 = \frac{1}{2}$ より主張が従う。

主張から導出できる面積公式

最後に、主定理から証明できる少し変わった面積公式を紹介します。
下記の事実が成り立ちます。

（少し変わった面積公式）

三角形の三辺 $a, b, c$ と対応する三角 $A, B, C$ を用いて三角形の面積 $S$ は次のようにあらわされる。
$S = \frac{1}{4} (\frac{a^{2}}{\tan A} + \frac{b^{2}}{\tan B} + \frac{c^{2}}{\tan C})$

この事実の証明のために、次の命題を用います。

（第一余弦定理）

三角形の三辺 $a, b, c$ 及び対応する三角 $A, B, C$ の間に次の関係式が成り立つ。

$a = b \cos C + c \cos B$
$b = c \cos A + a \cos C$
$c = a \cos B + b \cos A$

なお、「第一」というからにはもちろん「第二余弦定理」も存在します。実はこれは通常単に「余弦定理」と呼ばれている主張です（命題 $5$ ）。初等幾何の中では「第二」の方が主たる位置を占めているからかこの第一余弦定理はあまり見ることがありません。故に「第一・第二」の区別もなくなり、「余弦定理」の名は命題 $5$ の方に集約されてしまっているようです。

（少し変わった面積公式）

第一余弦定理を用いて、次のように変形を行う。

$\begin{aligned} (a + b + c) (\cos A + \cos B + \cos C) & = (b \cos C + c \cos B) + (c \cos A + a \cos C) + (a \cos B + b \cos A) + (a \cos A + b \cos B + c \cos C) \\ (a + b + c) β & = (a + b + c) + (a \cos A + b \cos B + c \cos C) \\ (a + b + c) (β - 1) & = a \cos A + b \cos B + c \cos C \end{aligned}$

ここで、 $t := \frac{1}{2} (a + b + c)$ とおく。また、主定理を用いて $β - 1 = \frac{r}{R}$ と置き換える。すると、「内接円の半径による面積公式」から、左辺は次のように変形できる。

$(a + b + c) (β - 1) = 2 t (\frac{r}{R}) = \frac{2 S}{R}$

これより、

$\begin{aligned} \frac{2 S}{R} & = a \cos A + b \cos B + c \cos C \\ 4 S & = 2 R (a \cos A + b \cos B + c \cos C) \\ 4 S & = 2 R a \cos A + 2 R b \cos B + 2 R c \cos C \end{aligned}$

ここで、正弦定理を用いれば、

$\begin{aligned} 4 S & = (\frac{a}{\sin A}) a \cos A + (\frac{b}{\sin B}) b \cos B + (\frac{c}{\sin C}) c \cos C \\ = a^{2} (\frac{1}{\frac{\sin A}{\cos A}}) + b^{2} (\frac{1}{\frac{\sin B}{\cos B}}) + c^{2} (\frac{1}{\frac{\sin C}{\cos C}}) \\ = \frac{a^{2}}{\tan A} + \frac{b^{2}}{\tan B} + \frac{c^{2}}{\tan C} \end{aligned}$

を得る。これを整理して主張が従う。

終わりに

三角形の外接円と内接円の関係について書きました。
この内容は、私が中学生から高校生くらいの間に考えていたことをまとめなおしたものです。当時は三角比を用いることで平面幾何の色々な公式が次々に導出できることが大変面白く、夢中になって考え込んでいました。
当時から時間がたった今まとめなおしてみると、論証が危うかったところも多く、修正のためそれなりに時間を使うことになりました。それでも、記事作成中は当時の感覚を思い出してなかなか懐かしい心持でした。

なお、記事中の図式作成には GeoGebra というサイトを利用しました。直感的に作図ができるのでかなり助けられました。

この記事に関してコメントや誤植等がありましたらぜひお知らせください。

投稿日：2024年12月1日

更新日：2024年12月2日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

Summation

13642

他の人のコメント

コメントはありません。

読み込み中

Summation

三角形の内接円と外接円の相似比

主定理とその例
主定理の証明
特別な三角形に対する系
$β$ 定数の存在範囲
主張から導出できる面積公式
終わりに

三角形の内接円と外接円の相似比

主定理とその例

主定理の証明

特別な三角形に対する系

β 定数の存在範囲

主張から導出できる面積公式

終わりに

この記事を高評価した人

この記事に送られたバッジ

投稿者

コメント

他の人のコメント

$β$ 定数の存在範囲