欠損チェス盤にドミノ・L型トロミノ・I型トロミノを敷き詰めたい
はじめに
この記事では、最近話題になった、一部が欠けたチェス盤にドミノやL型トロミノ、I型トロミノを敷き詰めることができるかどうかを判定する方法について解説していきます。
チェス盤上の位置を示すために、次のように「番地」を使うことにします。
例えば、左上の位置は" $a8$ "のように表します。
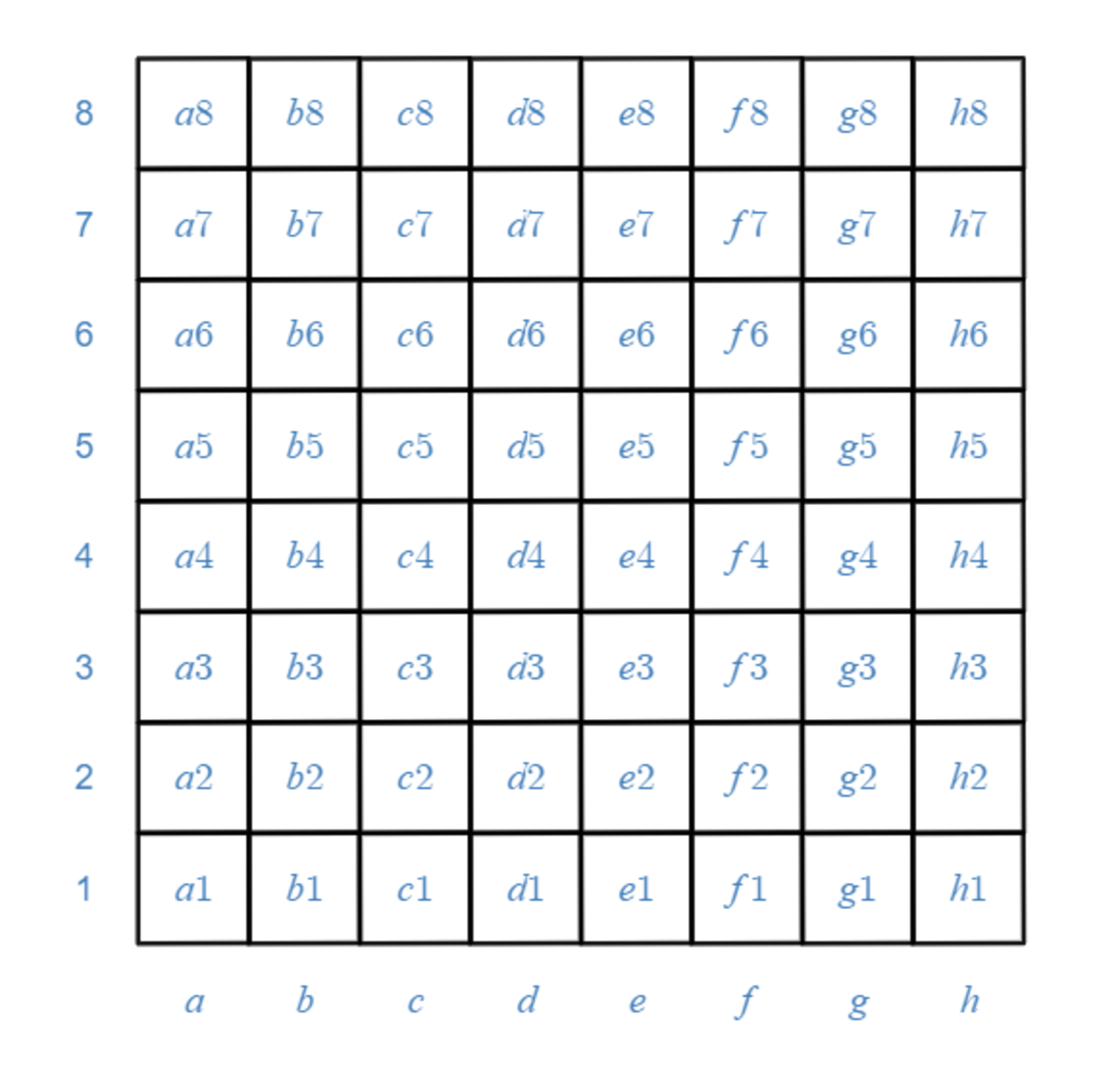 チェス盤の番地
チェス盤の番地
ドミノの場合
欠損チェスボードにドミノを敷き詰めることは可能か
まずは、一部が欠けたチェスボードにドミノを敷き詰められるかという、次のような問題を考えてみましょう。
下図のように、チェスボードの左上($a8$)と右下($h1$)を欠けさせたものに、$2$ マス分の大きさのドミノを重ならないように敷き詰めていきます。はたして、$31$ 枚のドミノを重ならずに全て敷き詰めることは可能でしょうか?
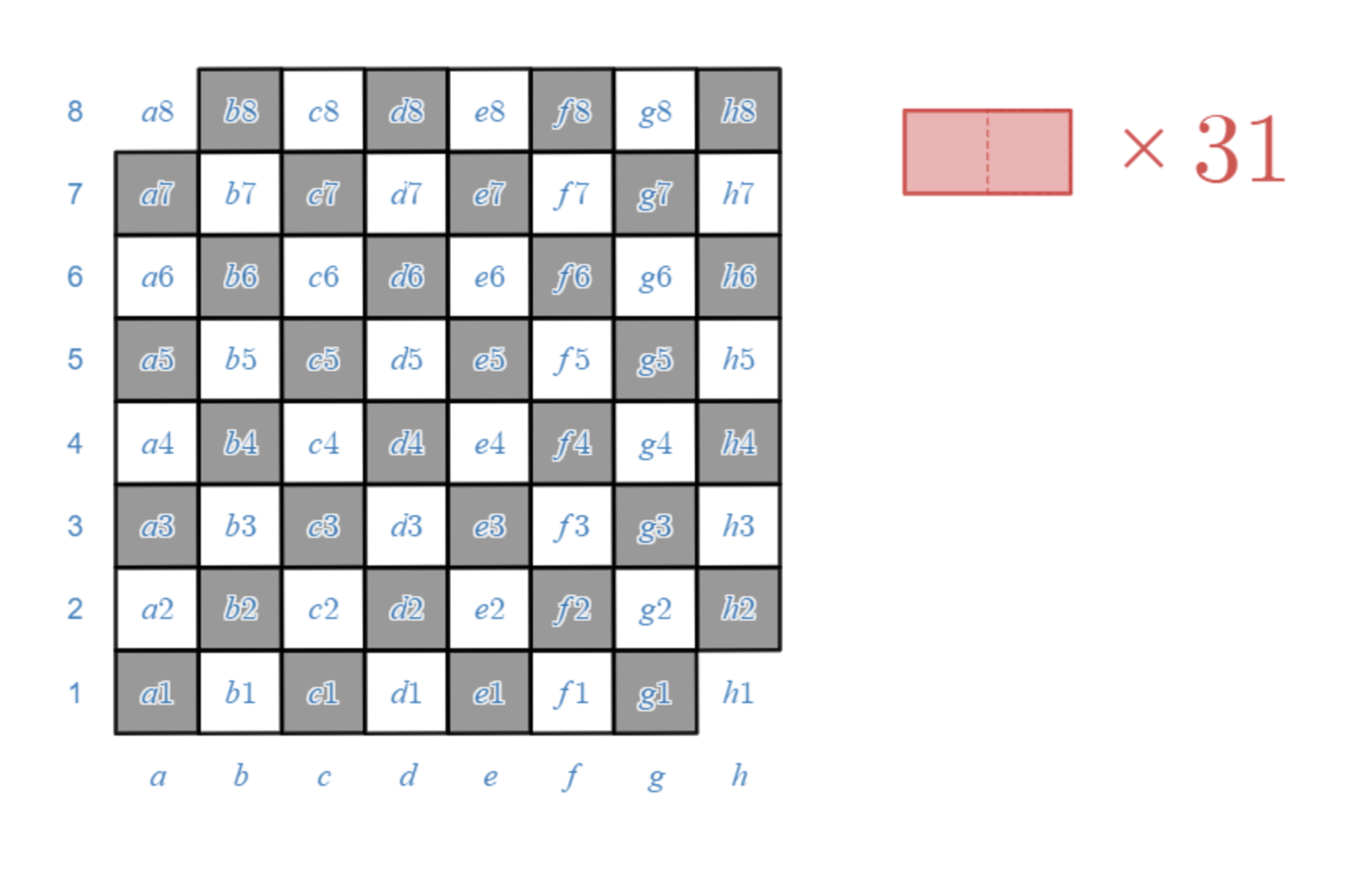 欠損チェスボードにドミノを敷き詰められるか
欠損チェスボードにドミノを敷き詰められるか
パズル好きの間では割と知られた問題ですが、私がこの問題とその解法を初めて見たときはその解法のエレガントさにとても感動したことを覚えています。
初めてこの問題を見たという人は少し考えてから答えを見てください。
答え
欠損チェスボード上の黒マスと白マスの数を数えると、黒いマスは $32$ マス、白いマスは $30$ マスとなっています。
ドミノ $1$ 枚を配置するごとに黒マスと白マスが $1$ 枚ずつ隠されていきますから、$30$ 枚のドミノを配置したところで必ず黒マスが $2$ マス余ってしまい、これを $1$ 枚のドミノで隠すことは不可能です。
具体的な配置を一切考えていないにもかかわらず、不可能であることが一瞬で理解できてしまう、実にエレガントな答えだと思います。
派生問題
上の問題を少し変えて、黒マスと白マスを $1$ 枚ずつ欠けさせた場合には、ドミノを全て敷き詰めることはできるでしょうか?
実は、黒マスと白マスを $1$ 枚ずつ欠けさせた場合には、どの位置を欠けさせたとしても、必ずドミノを敷き詰めることができることが知られています。さらに一般化して、次のような問題を考えました。
m,nを積mnが4以上の偶数となるような2以上の自然数の組とします。このとき「白と黒を1マスずつランダムに欠けさせた一般化チェスボード(m×nマス)であればドミノ(1×2マス)を必ず敷き詰められる」ことを証明してください。
— apu (@apu_yokai) March 16, 2022
この問題には、いろいろな解法がよせられました。
私が想像もしなかった面白い解法がいろいろよせられましたのでご紹介します。
2つの長方形(どちらも偶数マス)に分割して、それぞれが敷き詰められればOK。それぞれ1個ずつ欠けた長方形の場合は、両方にまたがるドミノを1個使う。これを再帰的に適用すれば最終的に敷き詰められることが分かる
— べーた🌘TCM-β (@tcmbeta) March 16, 2022
盤面全体に1つのループを構築すると、抜いたマスによって分断された2つの線は長さが偶数なので、端から順にドミノを並べていけば敷き詰められる。
— TokusiN (@toku51n) March 16, 2022
僕が知っている証明もこちらです。ネットで見つけた文献(問題4.)を貼り付けときますね。通常のチェス盤でやっていますが、一般化しても同様にループを構成出来ます。https://t.co/NCNqS1B3Le
— tokunaga shin-ichi (@shin1toku) March 17, 2022
トロミノの場合
チェス盤にL型トロミノを1マスを除いて敷き詰めることは可能か
下図右側のように $3$ つの正方形をL字型につないだものを「L型トロミノ」と呼びます。
チェスボードの中の $1$ マスをランダムに欠けさせたものにL型トロミノを $21$ 枚重ならないように敷き詰めることは必ず可能です。そのことを証明してください。
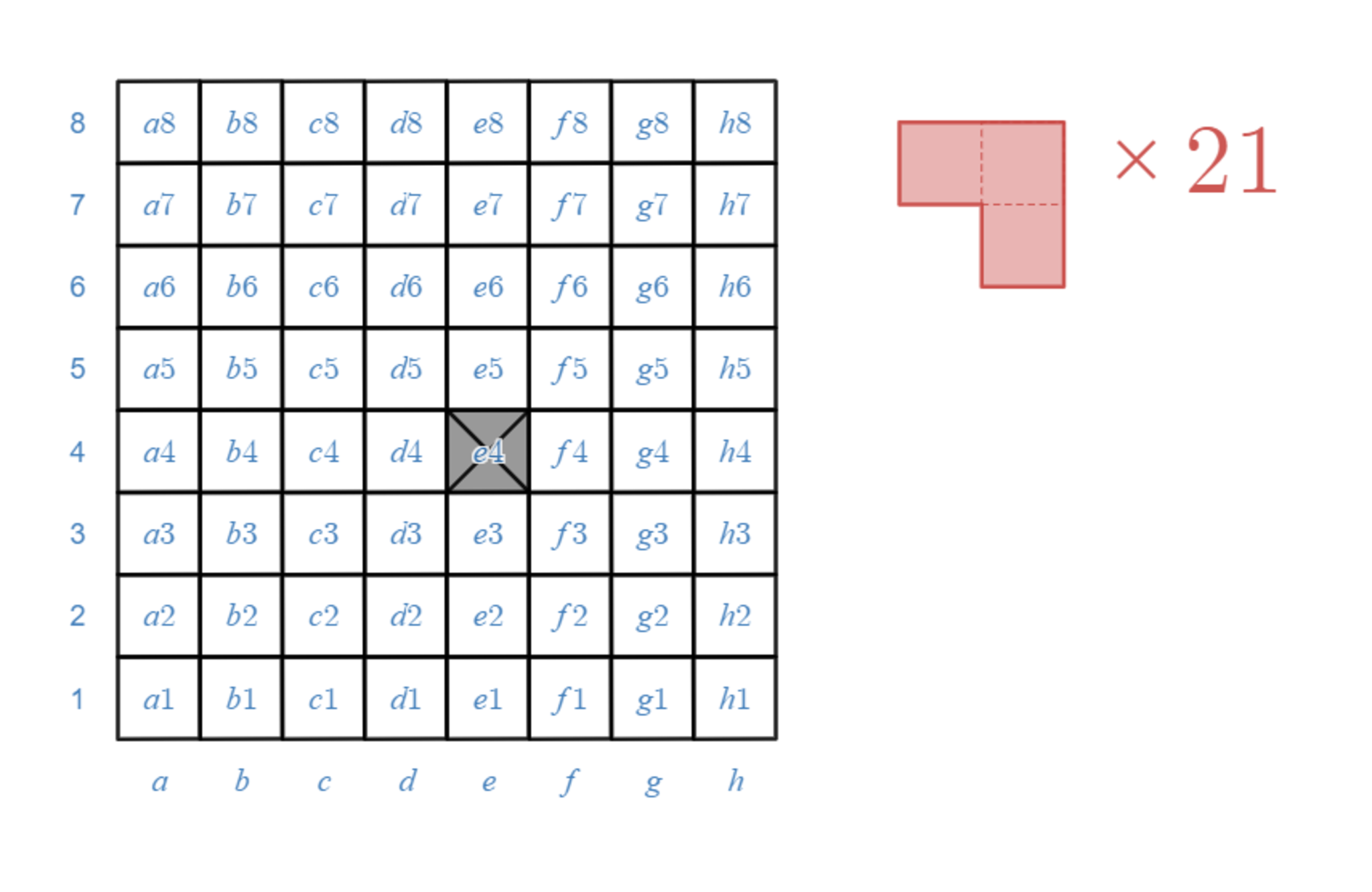 欠損チェスボードにLトロミノを敷き詰めることができるか
欠損チェスボードにLトロミノを敷き詰めることができるか
答え
厳密な証明ではないですが、ここでは考え方を図解することで略解とします。
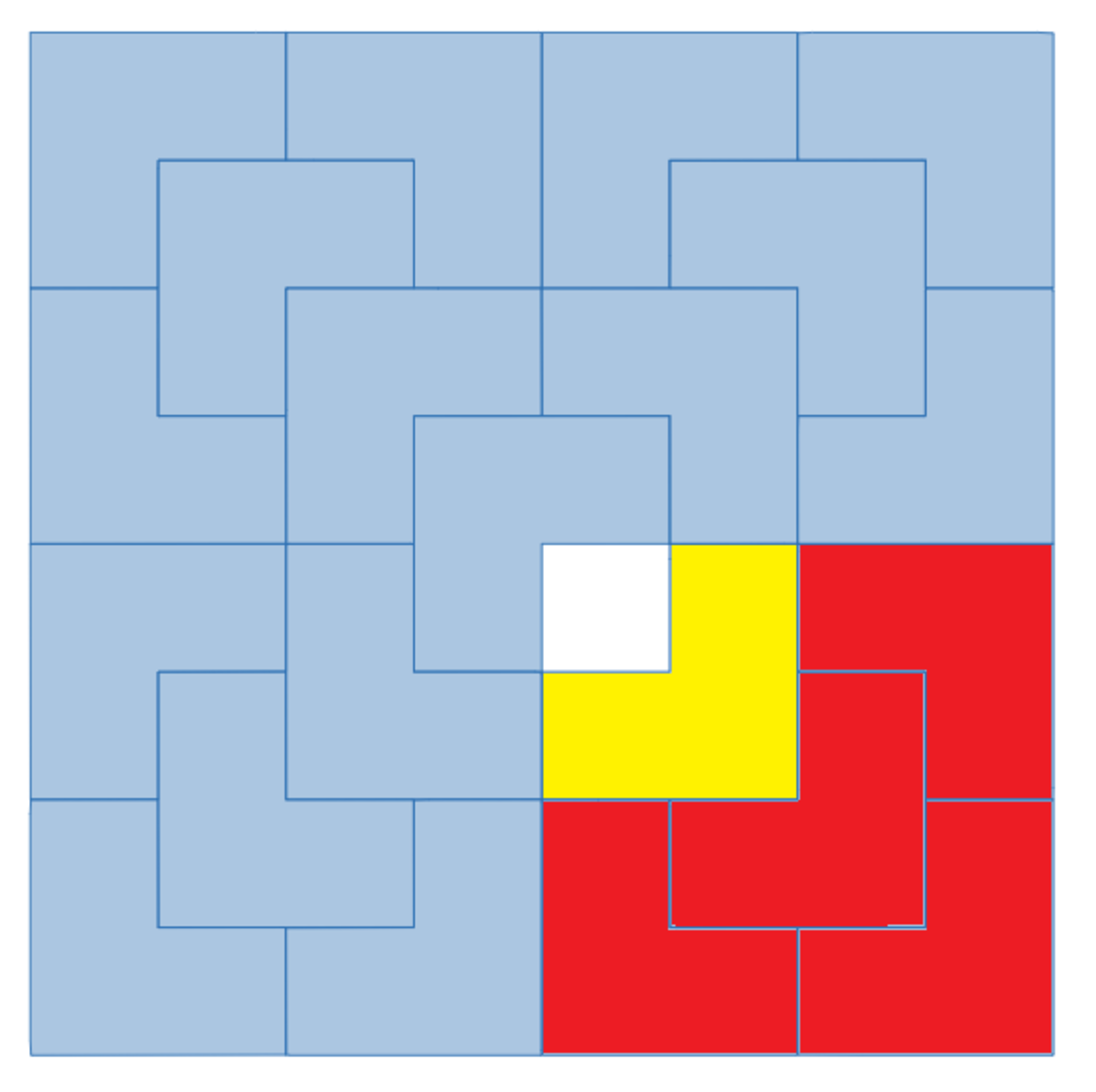 再帰的に敷き詰める
再帰的に敷き詰める
上図の赤い部分をみると、黄色いLトロミノ$4$個分を使って、黄色いLトロミノとの相似比 $2$ 倍のLトロミノを形作っていることがわかります。
また、青い部分をみると、赤いLトロミノ$4$個分を使って、黄色いLトロミノとの相似比 $4$ 倍のLトロミノを形作っていることがわかります。
このように再帰的に配置することによって、どのマスが欠けている場合であってもLトロミノを $21$ 枚重ならないように敷き詰めることは可能です。
2のべき乗の大きさに一般化できる
再帰的な構造をしていることから、元となる正方形の一辺の長さが $2^n$ マス分の場合は同じ方法で敷き詰められることもわかります。
一辺が2^nマス分の正方形から1マス抜いた形はトロミノで敷き詰められるの図 pic.twitter.com/opAzRODP1r
— apu (@apu_yokai) March 17, 2022
リンク先に動画がありますのでご覧ください。(動画のファイルサイズが大きすぎてMathlogにはアップロードできませんでした。)
なお、この敷き詰め方法を題材にした問題がOMC(Online Math Contest)で出題されたことがあるそうです。
問題へのリンク : OMC055(F)
チェス盤にI型トロミノを1マスを除いて敷き詰めることは可能か
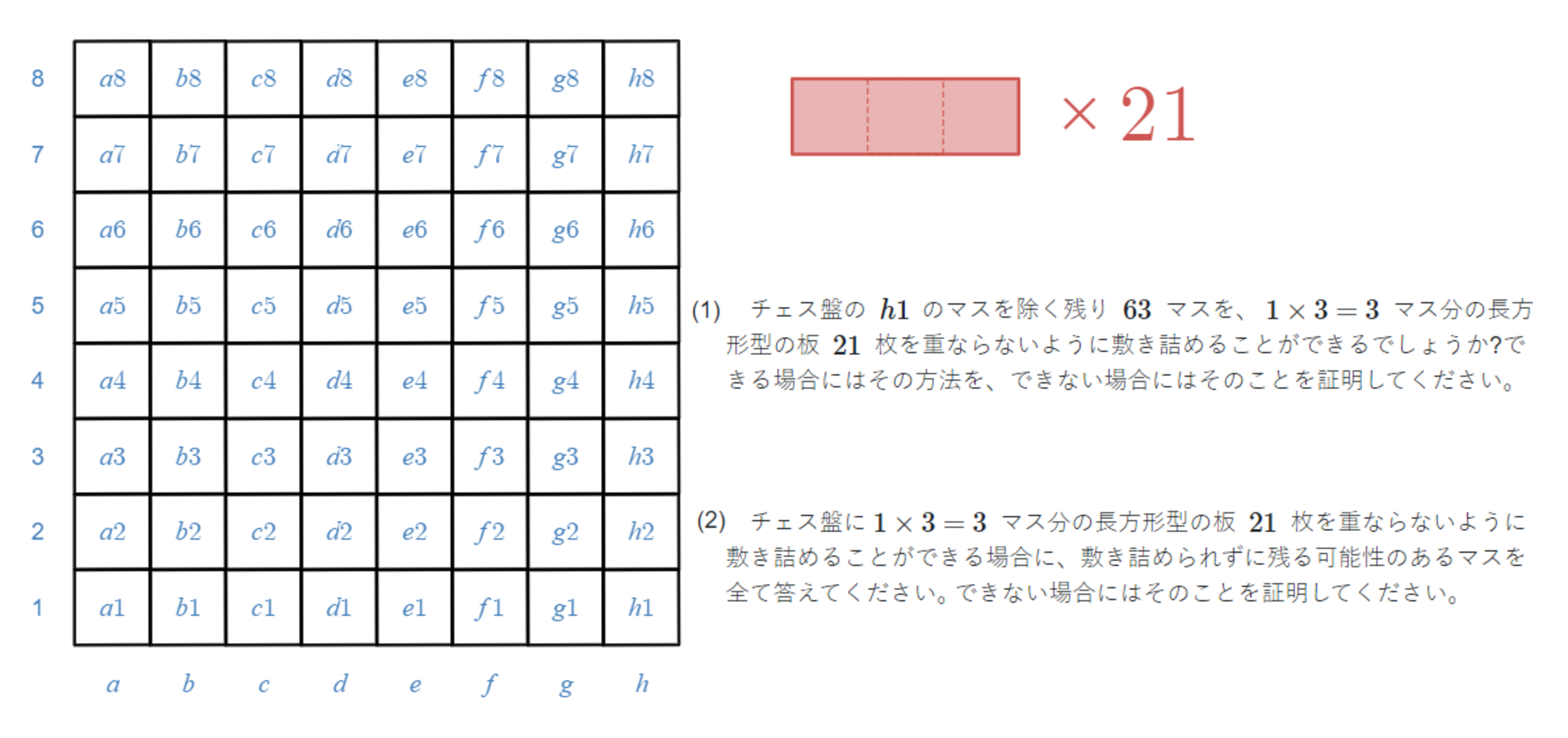 チェス盤にI型トロミノを敷き詰めることができるか
チェス盤にI型トロミノを敷き詰めることができるか
チェス盤の $h1$ のマスを除く残り $63$ マスに、$1\times3=3$ マス分の長方形型の板 $21$ 枚を重ならないように敷き詰めることができるでしょうか?できる場合にはその方法を、できない場合にはそのことを証明してください。
チェス盤に$1\times3=3$ マス分の長方形型の板 $21$ 枚を重ならないように敷き詰めることができる場合に、敷き詰められずに残る可能性のあるマスを全て答えてください。できない場合にはそのことを証明してください。
なお、$1\times3=3$ マス分の長方形型の板のことを「I型トロミノ」と呼びます。
この問題は、私が自分で考えたものです。
自分で考えた問題でありながら、答えが出たときに、あまりに予想外の答えだったので、本当にビックリするとともに、この面白さを誰かに伝えたいと思ったことを覚えています。
(投稿時のツイート)
数学の問題です。
— apu (@apu_yokai) March 21, 2022
チェス盤に1x3マス分の長方形21枚を敷き詰めることはできるでしょうか? (画像参照) pic.twitter.com/NlZWMXGPUv
答え
(1) の答え
このような敷き詰めは不可能です。そのことを証明します。
まず、下図のように盤面に $1$ ~ $3$ の数字を順番に書き込んでみましょう。
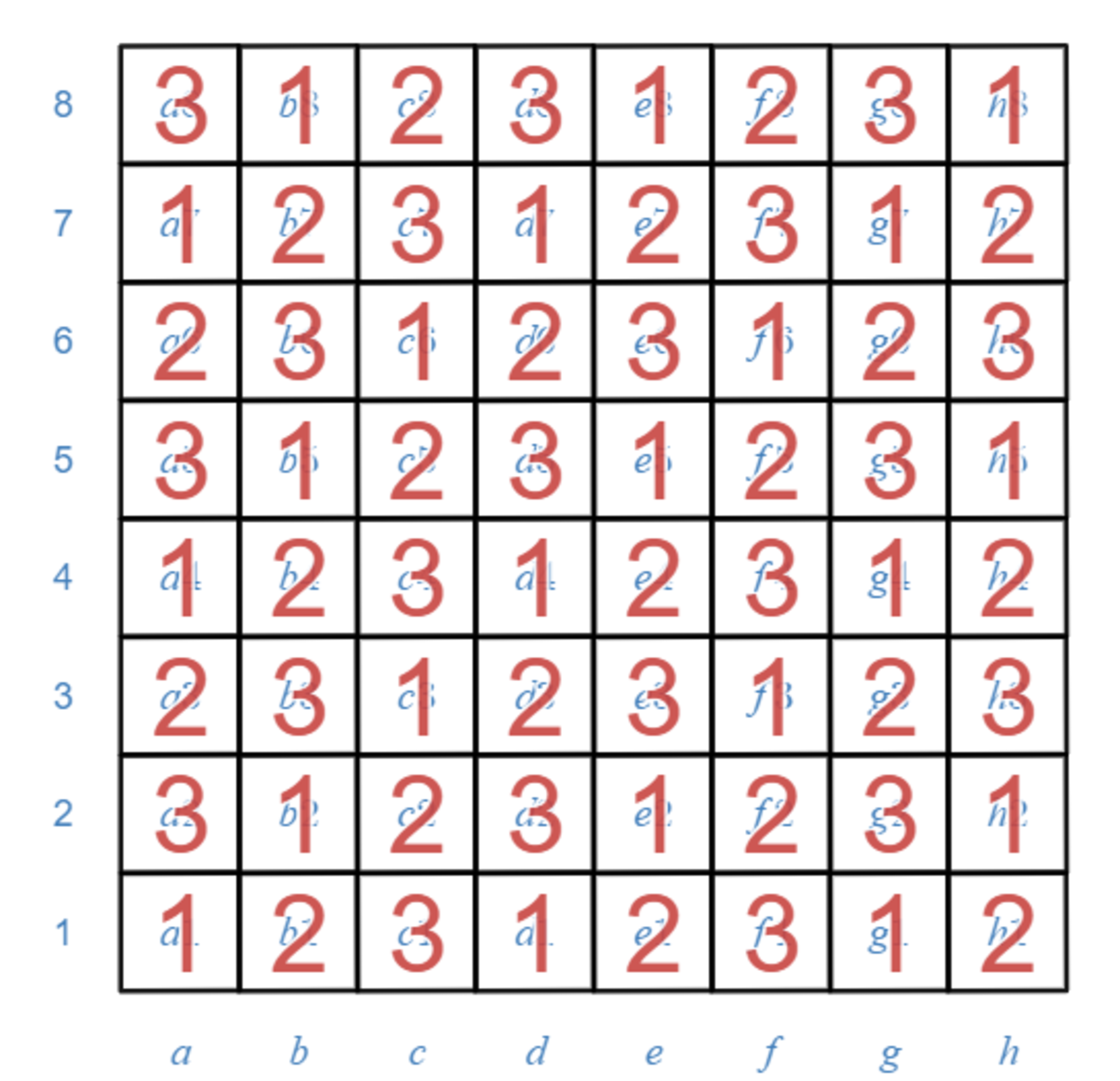 1~3の数字を順番に書き込む
1~3の数字を順番に書き込む
書き込まれた数字の数を数えるとこうなっています。
| 数字 | 個数 |
|---|---|
| $1$ | $22$ 個 |
| $2$ | $21$ 個 |
| $3$ | $21$ 個 |
$h1$ のマスを除くと、こうなります。
| 数字 | 個数 |
|---|---|
| $1$ | $22$ 個 |
| $2$ | $20$ 個 |
| $3$ | $21$ 個 |
ところが、長方形の板を配置する場合には、 $1,2,3$ をそれぞれ $1$ 個ずつ覆うようにしか配置できませんので、$20$ 枚目を配置した後は必ず $1$ のマスが $2$ 個、 $3$ のマスが $1$ 個あまってしまい、$21$ 枚目を配置することはできません。
(証明終わり)
(2) の答え
まず、(1)のときと同じように盤面に $1$ ~ $3$ の数字を順番に書き込んでみましょう。
 1~3の数字を順番に書き込む
1~3の数字を順番に書き込む
| 数字 | 個数 |
|---|---|
| $1$ | $22$ 個 |
| $2$ | $21$ 個 |
| $3$ | $21$ 個 |
書き込まれた数字の数のうち、$1$ だけが$1$個多いですから、長方形の板を $21$ 枚配置できたとして、最後に残るマスとなりえるのは、盤面上に $1$ を書き込んだマスしかありえません。
また、数字の書き込み方法を左右反転しても同じことが言えますので、数字の書き込み方法を左右反転しても数字が $1$ になるマスだけが最後に残る可能性のあるマスということになります。もとの配置を赤、左右反転した配置を緑で重ねて書くと次のようになります。
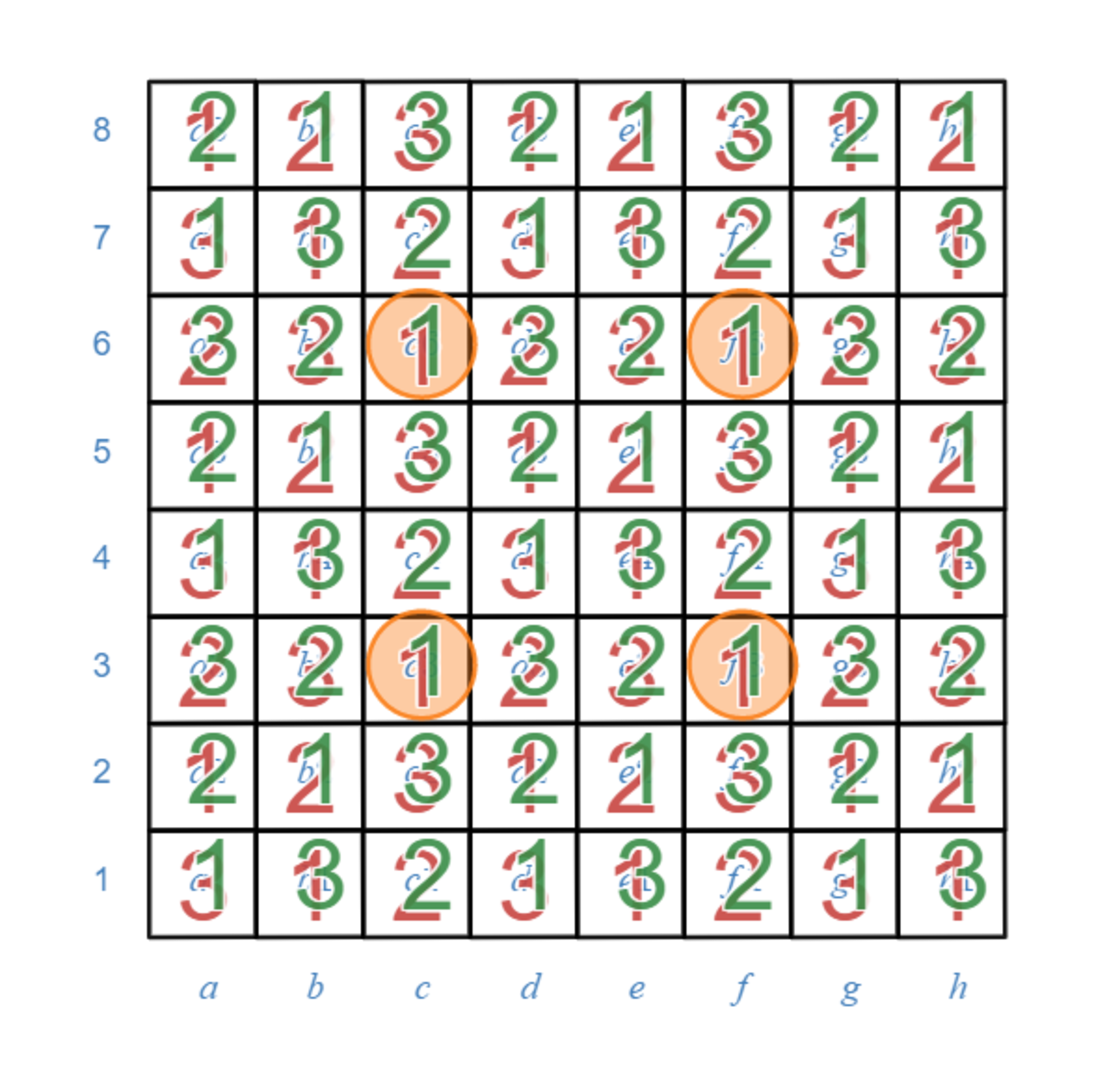 左右反転しても「1」が配置されるマスは4つだけ
左右反転しても「1」が配置されるマスは4つだけ
そうすると、可能性のあるマスは $c3,c6,f3,f6$ の $4$ マスだけです。
そこで、これらのマスを残して長方形の板 $21$ 枚を配置することが可能かどうか調べてみると、例えば次のように配置することができます。
![c3を残して !FORMULA[70][1122081][0] 枚の板を配置する例](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220329200821.png?alt=media) c3を残して $21$ 枚の板を配置する例
c3を残して $21$ 枚の板を配置する例
例として $c3$ のマスを残す配置の例をあげました。(他にも配置方法はあります)
$c6,f3,f6$ のマスを残す場合も、この配置を $90$ 度ずつ回転してやれば可能ですね。
したがって、敷き詰められずに残る可能性のあるマスは、 $c3,c6,f3,f6$ の $4$ マスです。
別解について
この問題をツイートしたところ、私の想定していたものより素晴らしい別解が出ましたのでご紹介したいと思います。
まずはヒドリさんのこちら。
https://t.co/FDv2Hkl2uZ
— ヒドリ (@HydryHydra) March 22, 2022
29429429
75375375
61861861
29429429
75375375
61861861
29429429
75375375
マスに↑の数字を当てはめるとタイルをどこにおいても合計が15になるが、一方で全マス足して15で割ったあまりは8なので8に対応するc3c6f3f6があまる 前にもやったけど正攻法は知らぬ
魔方陣を使うことで、一気に残り得るマスの候補を $4$ マスにしぼっています!
これはエレガントですね!
感動したので動画にしてみました。
![魔方陣の配置を敷き詰めると!FORMULA[77][1121244][0]ずつ隠れて「8」が残る](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220329221536.gif?alt=media) 魔方陣の配置を敷き詰めると$15$ずつ隠れて「8」が残る
魔方陣の配置を敷き詰めると$15$ずつ隠れて「8」が残る
さらに、ベータさんからはこんな別解をいただきました。
別解ですどうぞ
— べーた🌘TCM-β (@tcmbeta) March 25, 2022
11011011
11011011
00200200
11011011
11011011
00200200
11011011
11011011
これも動画にしてみました。
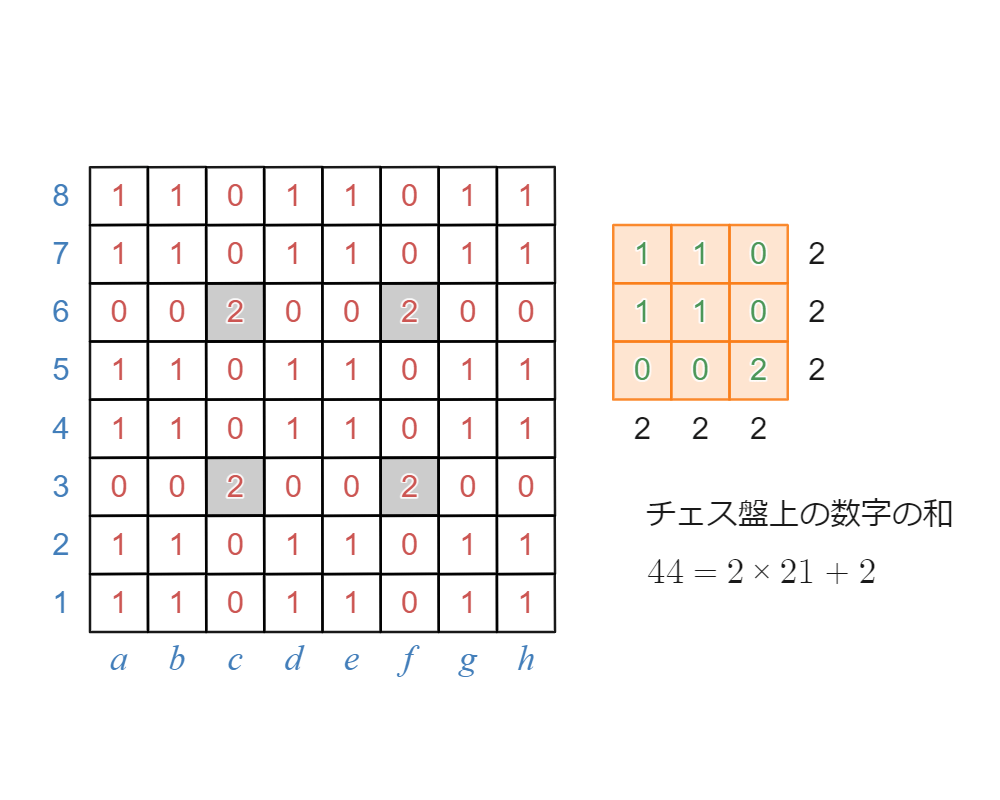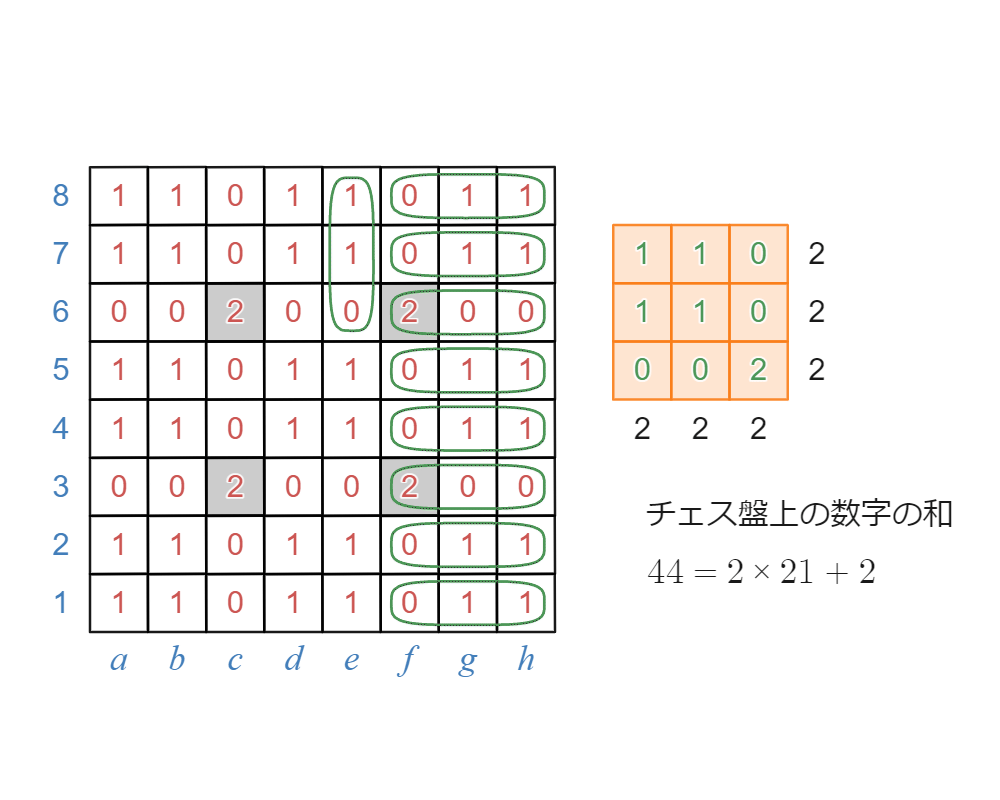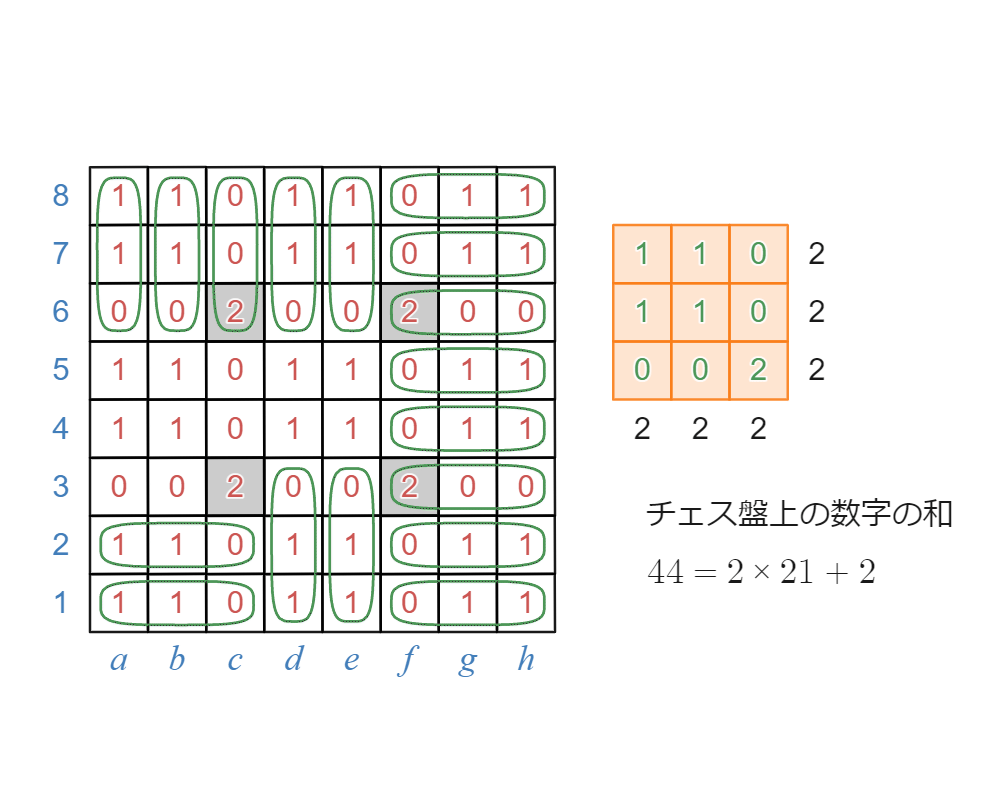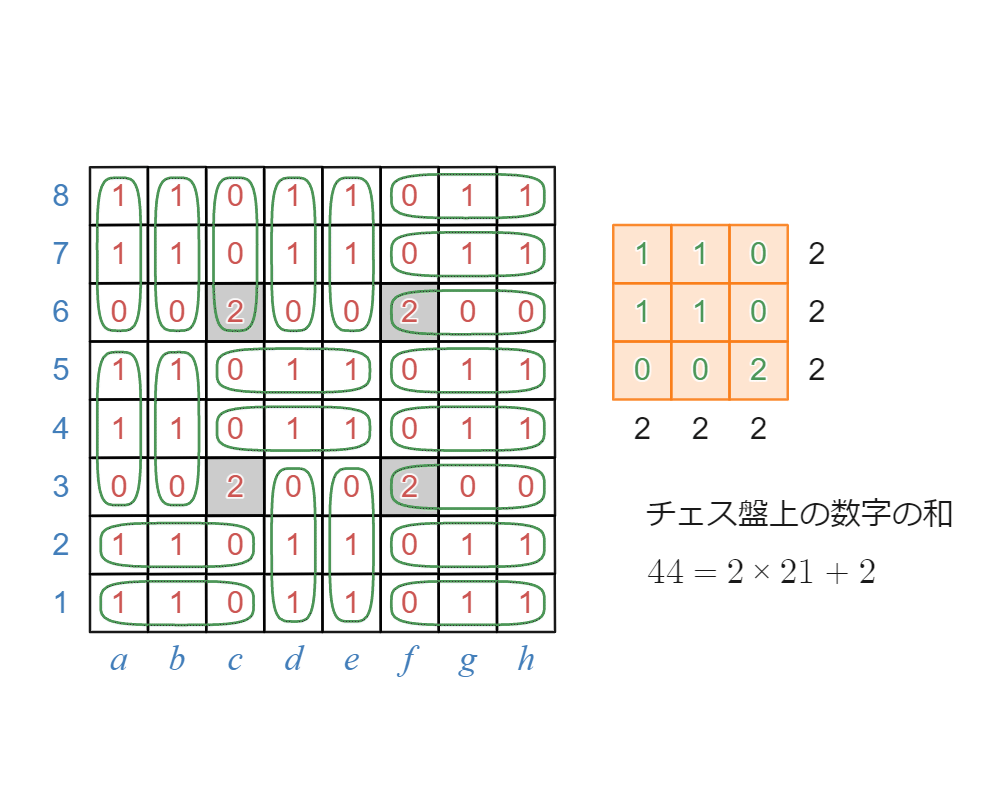 縦横の和が2となる配置で敷き詰める
縦横の和が2となる配置で敷き詰める
通常の魔方陣はナナメの和も $15$ になりますが、今回の問題ではナナメは考えなくていいので、ここまでシンプルな配置でもいいんですね。
これまたスマート!
この配置は、次のような発想で思いついたそうです。なるほど!
じつは、
— べーた🌘TCM-β (@tcmbeta) March 25, 2022
01001001
10010010
00100100
01001001
10010010
00100100
01001001
10010010
これと、これの鏡像との重ね合わせだったりします
おわりに
元になるドミノ敷き詰め問題は答えを知っていた人も多いと思います。しかし、I型トロミノを敷き詰めるときに、特定の4マスだけしか残る可能性がないということは、おそらくほとんどの人が知らなかったのではないでしょうか。
こんな風に、有名問題を少しアレンジするだけで、非自明な結果が出てくるのってとても面白いですね。
この敷き詰め問題は、まだまだいろいろな派生問題を作るポテンシャルを秘めていると思います。
新しい問題を作ったら、是非教えてほしいと思います。挑戦しますよ!
