JMO2012本選問4を解こう(直交座標)
そうだ,計算しよう-------
ということでJMO2012問4を直交座標で鮮やかに解きます．
問題
平面上に三角形$PAB$と$PCD$がある．$PA=PB,PC=PD$であり,$P,A,C$および$B,P,D$はそれぞれこの順に同一直線上にある．$A,C$を通る円$S_1$と$B,D$を通る円$S_2$が異なる2点$X,Y$で交わっているとする．このとき,三角形$PXY$の外心は$S_1$の中心と$S_2$の中心であることを示せ．
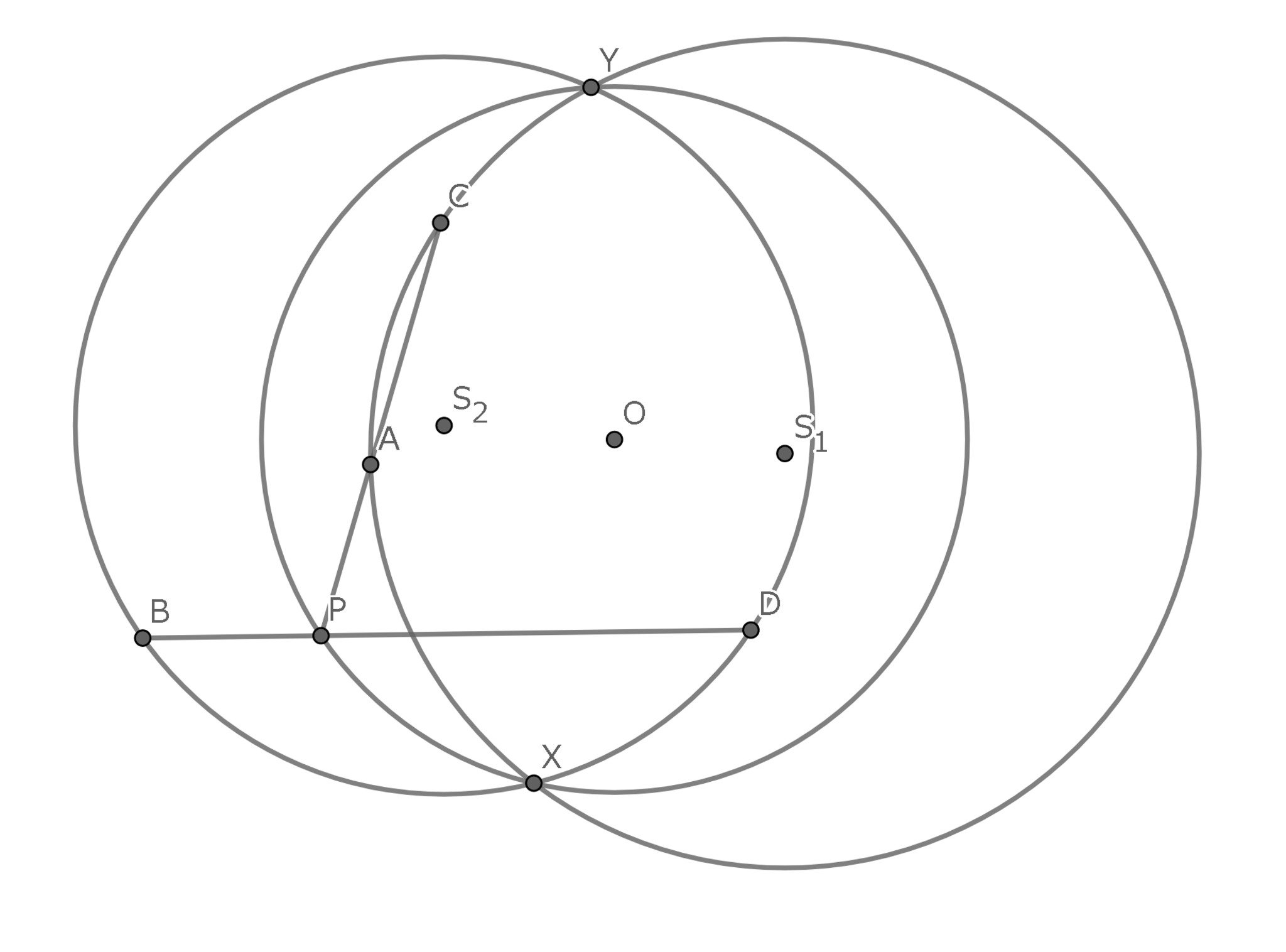図
解いてみた
図形の自由度が高そうでさすが4番に置かれているだけあります．
図から明らかですが束の原理がぶっ刺さります．
一致法で示す.すなわち$S_1S_2$の中点を中心とし,$X,Y$を通る円$S$が$P$を通ることを示せば十分である．
$a,c$を正の実数として$P(0,0),B(a,0),D(-c,0)$とおく．
また,条件より$s^2+t^2=1$を満たす正の実数$s,t$を用いて$A(sa,ta),C(sc,tc)$とおける．
$$S_1:x^2+y^2+l_1x+m_1y+n_1=0$$
$$S_2:x^2+y^2+l_2x+m_2y+n_2=0$$
とおくと$S$は$\dfrac{(S_1式)+(S_2式)}{2}$で表されるので,
$$S:x^2+y^2+\dfrac{l_1+l_2}{2}x+\dfrac{m_1+m_2}{2}y+\dfrac{n_1+n_2}{2}=0$$
ここで$A,C$が$S_1$上に,$B,D$が$S_2$上にあることより,次の4式が成り立つ．
$ \begin{eqnarray}
\left\{
\begin{array}{l}
a^2+l_1sa+m_1ta+n_1=0\\
c^2+l_1sc+m_1tc+n_1=0\\
a^2+l_2a+n_2=0\\
c^2-l_2c+n_2=0
\end{array}
\right.
\end{eqnarray} $
$c\times(第1式)-a\times(第2式)$および$c\times(第3式)+a\times(第4式)$より,
$ \begin{eqnarray}
\left\{
\begin{array}{l}
ac(a-c)-(a-c)n_1=0\\
ac(a+c)+(a+c)n_2=0
\end{array}
\right.
\end{eqnarray} $
$a-c,a+c\neq0$より$n_1+n_2=ac-ac=0$を得る．
したがって$P(0,0)$が$S$上にある．これが示したいことであった．$\square$
中心の中点なので「式の中点」をとることでピンポイントで方程式を立式できるのがミソです．すごくないですかこれ?
この記事を高評価した人
この記事に送られたバッジ
投稿者
