"幾何の視点"から不等式を見る
目次
- はじめに
- "幾何の視点"とは？
- 実践問題・解説(ヒント)
- 実践問題の解答
- おわりに
1.はじめに
この記事は不等式を幾何的視点で考察することによって見通しをよくすることを目的としています.
また,実践問題にはそれぞれ解説と解答がついています.解説は最後まで読むとほぼ問題を理解できる内容になっていますのでヒントとして使いたい場合は適宜途中まで読み進める形で利用してください.解答では,実際に答案で書くときの形式での例を載せています.
この記事では$|XX|$でXXの距離・長さを表します.
2."幾何の視点"とは？
幾何的な考察を用いることで簡単に不等式を示せるケースがあります.そのような場合は大抵代数的にゴリ押すよりも幾何的な考察を用いたほうが計算量が少なく済みます.ちなみに,代表的なものとして三角不等式やトレミーの不等式,オイラーの不等式などがあります.幾何的な不等式に気づくヒントとして,三平方の定理のような形だったり,三角関数の和のような構図があったりします.
ちなみに,不等式の問題に「三角形の三辺である」と言った条件が付け加えられることもあります.このような不等式は大抵Ravi変換だったりというテクニックを用いて代数的に解いていくことが多いです.このように,幾何的条件→代数的考察のパターンも存在します.今回は,代数的条件→幾何的考察のパターンを中心に解説していきます.
では,具体例を見てイメージを掴んでみましょう.
具体例
$a,b$を正の実数とする.この時,以下の不等式を示せ.
$$
\frac{a+b}{2}\ge\sqrt{ab}\ge\frac{2ab}{a+b}
$$
解説
相加相乗調和平均は代表的な幾何的に考察できる不等式です.まずは,円を考えてみましょう.実際に図を描いてみると図1のようになります.(解説の最下部においておきます.)
$|CF|=a,|FD|=b$とすると,$左辺 = |AE|$,$中辺 = |FG|$,$右辺 = |GH|$となります.
図と不等式の各辺の対応
相加平均
半径を表しているので,単純に直径$a+b$の半分${\frac{a+b}{2}}$となります.相乗平均
方冪の定理より,$中辺^2=ab$となって,$中辺= \sqrt{ab}$となります.調和平均
三角形GFAと三角形GHFの相似に注目します.$\left|GH\left|:\left|GF\left|=\right|GF\right|:\right|GA\right|$となって,すでに$|GF|=\sqrt{ab},|GA|=\frac{a+b}{2}$が分かっているので,$|GH|=\frac{2ab}{a+b}$となります.
したがって図から,$\frac{a+b}{2}\ge\sqrt{ab}\ge\frac{2ab}{a+b}$が成立するとわかります.
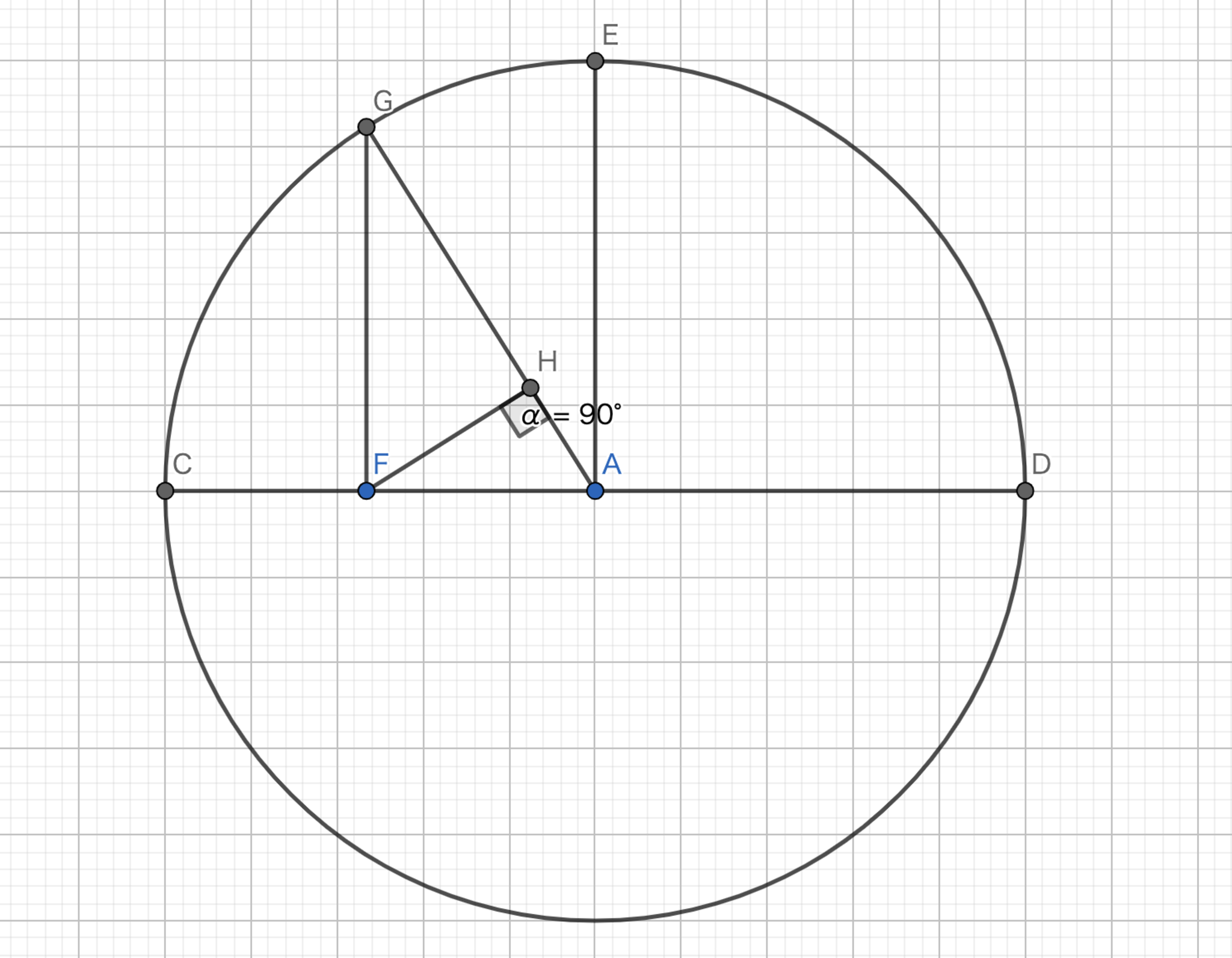相加相乗調和平均
このように,直感的に理解することができます.では,以下の実践問題を通してさらに理解を深めていきましょう.
実践問題
$a,b,x,y$を正の実数とする.この時,以下の不等式を示せ.
$$
\sqrt{\left(a^{2}+b^{2}\right)\left(x^{2}+y^{2}\right)}\ge\left(ax+by\right)
$$
解説・ヒント
コーシーシュワルツの不等式はベクトルを用いない初等的な証明もあります.相似な直角三角形を考えてみましょう.図2に注目してみてください.(解説最下部に示しておきます.)
今,三角形ABCと三角形EDAは相似な三角形です.その相似比を$a:b$,$|AB|:|BC|=x:y$とすると$|BD|=(ax+by)$,$|CE|=\sqrt{\left(a^{2}+b^{2}\right)\left(x^{2}+y^{2}\right)}$となります.これは,三角形ACE,ABC,EDAが全て直角三角形なので長さが計算できます.実際に計算してみると示したい式が得られるわけです.
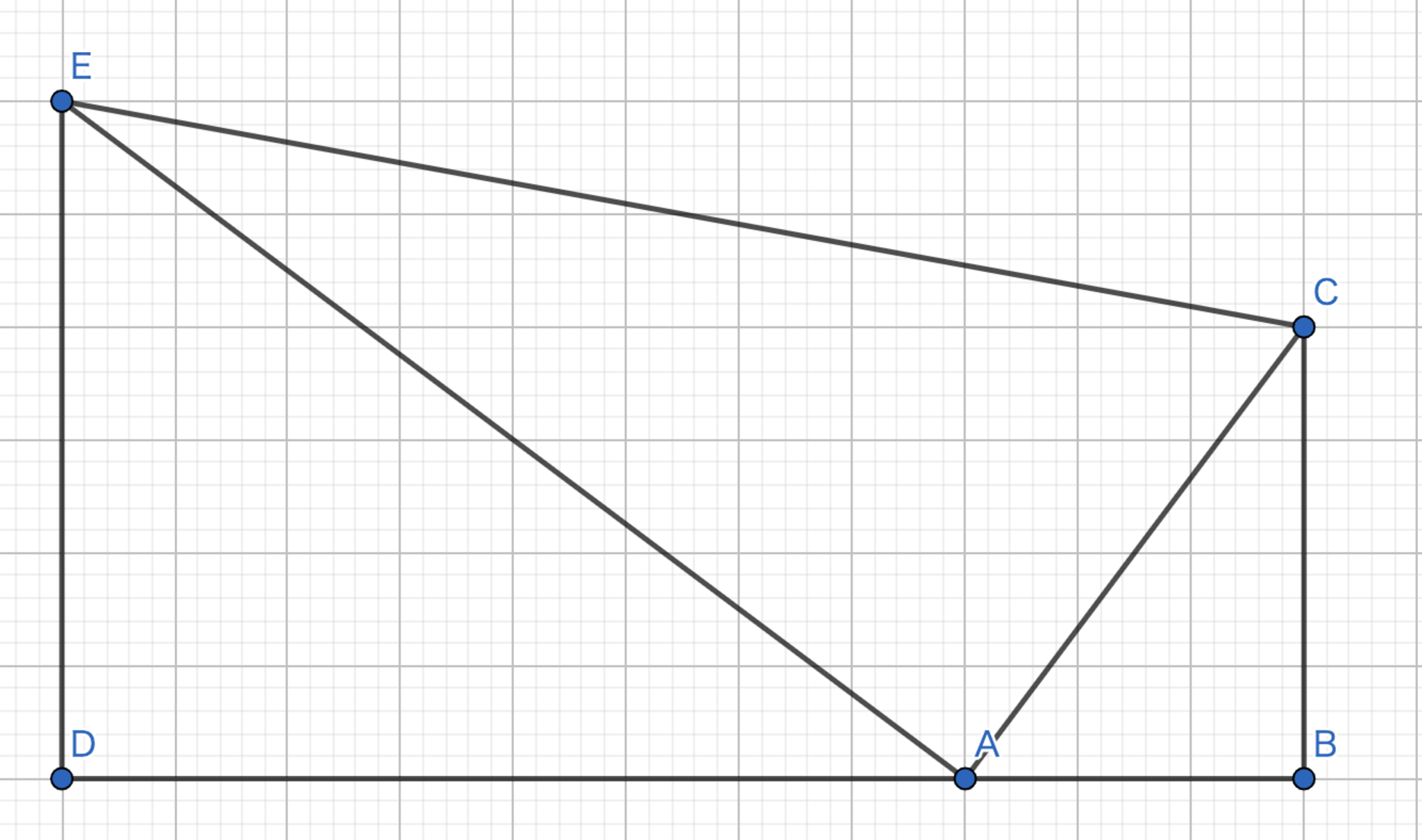コーシーシュワルツの不等式
$a,b,c$は$abc=a+b+c$を満たす正実数である.このとき,以下の不等式を示せ.
$$
\frac{a}{\sqrt{a^{2}+1}}+\frac{b}{\sqrt{b^{2}+1}}+\frac{c}{\sqrt{c^{2}+1}}\le\frac{3\sqrt{3}}{2}
$$
解説・ヒント
この問題は少しだけ強引な感じがしますが,こういうテクニックもある程度に見てもらえればなと思います.三変数の不等式で沼った時に幾何的手法も選択肢の一つにあると思ってもらえればなと思います.
$a+b+c=abc$という条件を幾何的条件に移していきましょう.まず,$a+b,b+c,c+a$を三辺とする三角形を考えます.このような三角形の成立条件は$a,b,c$が正の数であることと同値です.そして,そのような内接円の半径は$\sqrt{\frac{abc}{a+b+c}}$となりますが,$a+b+c=abc$なので,内接円の半径は$1$となります.このような状況下で不等式の左辺を評価していきましょう.
下の図では$|BE|=a, |CF|=b, |DG|=c$として,内接円の半径を$1$とします.すると,$\sqrt{a^{2}+1}=|AB|$,$\sqrt{b^{2}+1}=|AC|$,$\sqrt{c^{2}+1}=|AD|$となります.これは不等式の左辺に出てきますね.例えば,$X=\angle\mathrm{ABE}$,$Y=\angle\mathrm{ACF}$,$Z=\angle\mathrm{ADG}$とすると,不等式の左辺は$\cos X+\cos Y+\cos Z$となります.この時,$X+Y+Z=\frac{\pi}{2}$であることに注意しましょう.$cos \theta$は$0<\theta<\frac{\pi}{2}$では上に凸なので
$$\cos X+\cos Y+\cos Z\le3\cos\left(\frac{X+Y+Z}{3}\right)\ =3\cos\frac{\pi}{6}=\frac{3\sqrt{3}}{2}$$
が得られます.これを元の式に戻してみると,
$$ \frac{a}{\sqrt{a^{2}+1}}+\frac{b}{\sqrt{b^{2}+1}}+\frac{c}{\sqrt{c^{2}+1}}\le\frac{3\sqrt{3}}{2} $$
![内接円の半径が!FORMULA[44][36151][0]の三角形](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220524133742.png?alt=media)
内接円の半径が$1$の三角形
$k$を正整数とする.このとき,以下の不等式を示せ.
$$\sum_{n=1}^{6k}\sqrt{1+n^{2}}>\sum_{n=1}^{3k}\sqrt{4+\left(4n-1\right)^{2}}>\sum_{n=1}^{k}\sqrt{36+\left(36n-15\right)^{2}}$$
解説・ヒント
この不等式はルートの和になっていてとても証明しにくそうです.さらに,この不等式は交代的でも対称な形でもないので通常の不等式のようなエレガントな代数的アプローチも無さそうです.ですので,何か工夫して簡単に解ける方法がないか探していきます.
ここで,式の形に注目してみましょう.この式は平方和のルート.つまり,三平方の形になっているとわかると思います.試しに,$k=1$の時の図を書いてみましょう.
(図は解説の最下部に示しておきます.)
例えば,三角形DGJに注目すれば三角不等式より$|DG|+|GJ|>|DJ|$が得られます.同様に,残り二つの三角形に注目して得られる三角不等式を辺々足し合わせれば$k=1$における$左辺 > 中辺$がわかります.これは,kの値が大きくなってもやることは同じです.結局,三角不等式より$左辺 > 中辺$が成立するわけです.
同様の方法で$中辺 > 右辺$も考えていきましょう.例えば三角形DJPに注目すると三角不等式より$|DJ|+|JP|>|DP|$が得られます.さらに,三角形DPVに注目すると三角不等式より$|DP|+|PV|>|DV|$が得られます.よって,$k=1$における$中辺 > 右辺$も示すことができました.これはkの値が大きくなってもやることは同じです.結局,三角不等式より$中辺 > 右辺$となります.
したがって$左辺 > 中辺 > 右辺$が簡単に得られますね.
![!FORMULA[59][36494569][0]における左辺の図示](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220522164710.png?alt=media)
$k=1$における左辺の図示
![!FORMULA[60][36494569][0]における中辺の図示](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220522164834.png?alt=media)
$k=1$における中辺の図示
![!FORMULA[61][36494569][0]における右辺の図示](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220522164857.png?alt=media)
$k=1$における右辺の図示
$k$を正整数とする.このとき,以下の不等式を示せ.
$$
\sum_{n=1}^{k}\sqrt{n^{2}+\left(n+1\right)^{2}}\ge\sqrt{\left(\sum_{n=1}^{k}n\right)^{2}+\left(\sum_{n=1}^{k}\left(n+1\right)\right)^{2}}
$$
解説・ヒント
これも問題4と同様の考え方で解くことができます.下に図を示しておきますので参考にしてください.
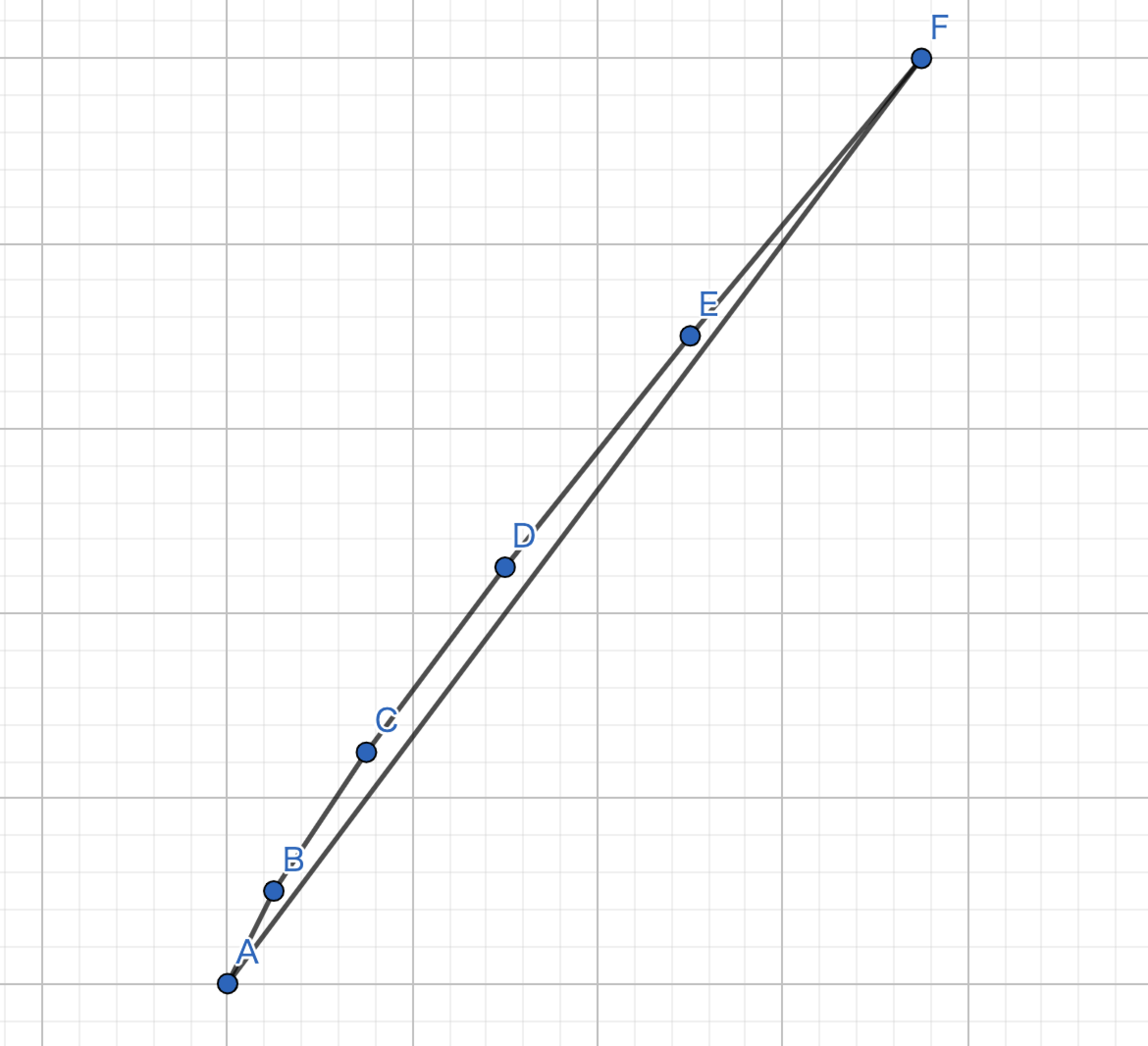k=5の幾何的解釈
4.解答
問題2
以下の図において,三角形ABCと三角形EDAは相似な三角形である.$|AB|:|BC|=x:y$,三角形ABCと三角形EDAの相似比を$a:b$とすると,
$$
|BD|=ax+by \\
|CE|=\sqrt{\left(a^{2}+b^{2}\right)\left(x^{2}+y^{2}\right)}
$$
ここで図より,明らかに$|CE| \geq|BD|$であるから題意は示された.
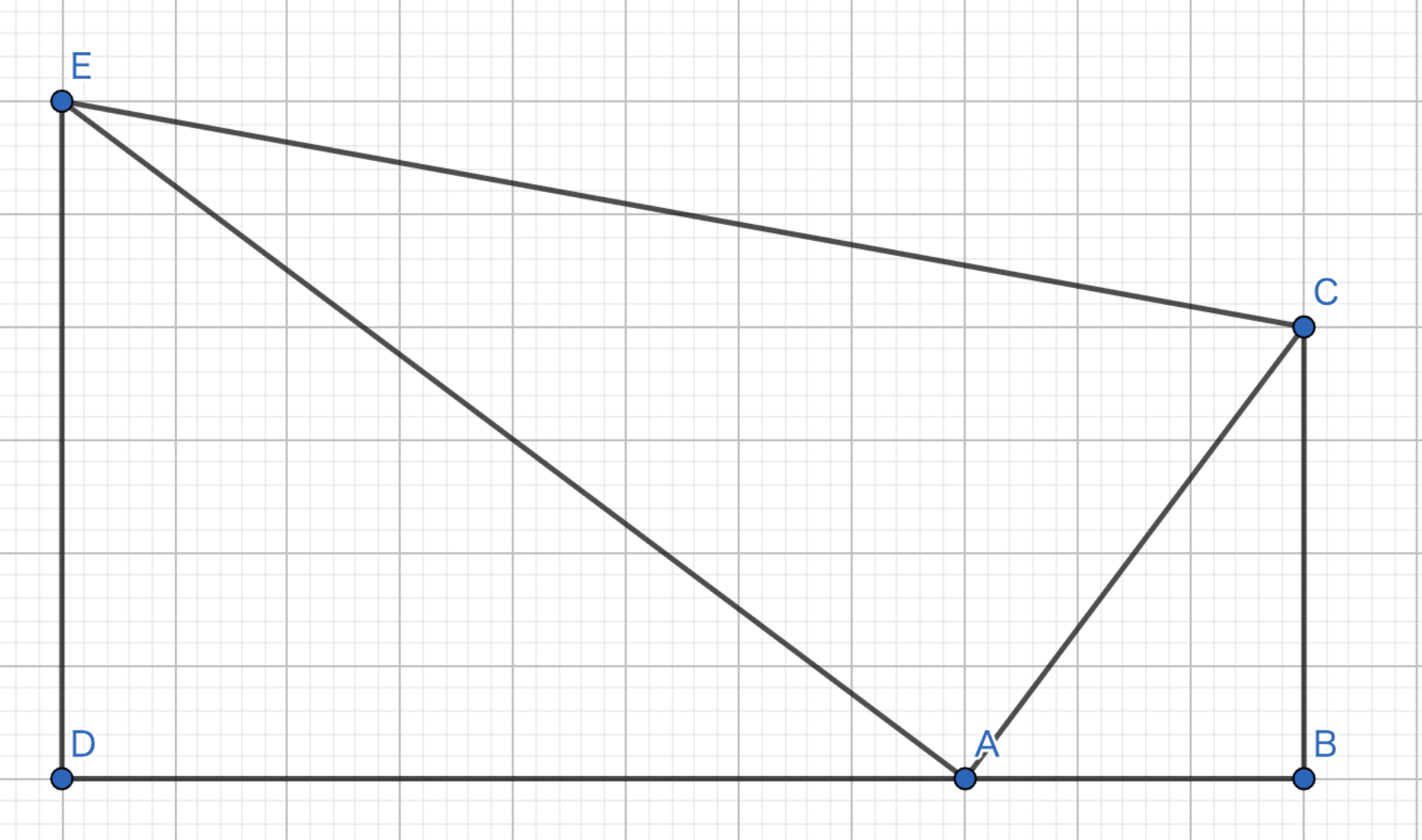コーシーシュワルツの不等式-解答用
問題3
以下の図において,$|BE|=a, |CF|=b, |DG|=c$とする.この時の三角形の成立条件は$a,b,c$が正と同値である.また,三角形DBCの内接円の半径は$\sqrt{\frac{abc}{a+b+c}}$であり$a+b+c=abc$より内接円の半径は$1$となる.したがって,$|AB|=\sqrt{a^{2}+1}$,$|AC|=\sqrt{b^{2}+1}$,$|AD|=\sqrt{c^{2}+1}$となる.この時,$X=\angle\mathrm{ABE}$,$Y=\angle\mathrm{ACF}$,$Z=\angle\mathrm{ADG}$とすると,不等式の左辺は$\cos X+\cos Y+\cos Z$となる.この時,$X+Y+Z=\frac{\pi}{2}$であることに注意せよ.$cos \theta$は$0<\theta<\frac{\pi}{2}$では上に凸なので
$$\cos X+\cos Y+\cos Z\le3\cos\left(\frac{X+Y+Z}{3}\right)\ =3\cos\frac{\pi}{6}=\frac{3\sqrt{3}}{2}$$
したがって,
$$ \frac{a}{\sqrt{a^{2}+1}}+\frac{b}{\sqrt{b^{2}+1}}+\frac{c}{\sqrt{c^{2}+1}}\le\frac{3\sqrt{3}}{2} $$
が得られて題意は示された.
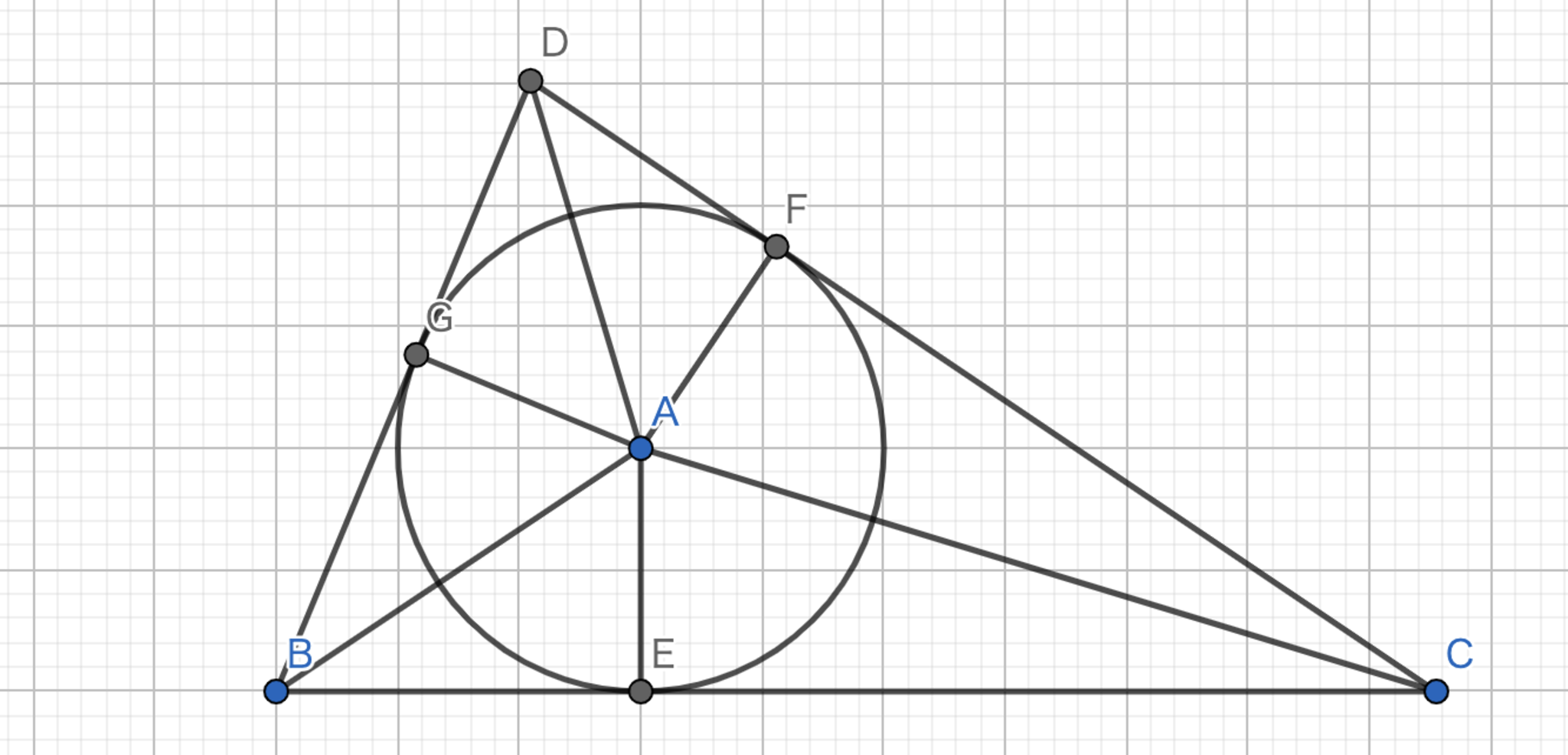問題3の不等式-解答用
問題4
$左辺>中辺$が成り立つことは
$$
\begin{align}
\sum_{n=1}^{3k}\left(\sqrt{\left(2n-1\right)^{2}+1}+\sqrt{\left(2n\right)^{2}+1}\right)>\sum_{n=1}^{3k}\sqrt{\left(4n-1\right)^{2}+4}
\end{align}
$$
が成り立つことと同値である.したがって,$\sqrt{\left(2n-1\right)^{2}+1}+\sqrt{\left(2n\right)^{2}+1}>\sqrt{\left(4n-1\right)^{2}+4}$を示せば十分である.図10において,$|AB|=2n-1,|BE|=2n$とすると$|DG|=\sqrt{\left(2n-1\right)^{2}+1},|GJ|=\sqrt{\left(2n\right)^{2}+1},|DJ|=\sqrt{\left(4n-1\right)^{2}+4}$となる.三角不等式より,$|DG|+|GJ|>|DJ|$であるから$左辺 > 中辺$は示された.
$ $
$中辺 > 右辺$が成り立つことは
$$
\sum_{n=1}^{k}\left(\sqrt{\left(4\left(3n-2\right)-1\right)^{2}+4}+\sqrt{\left(4\left(3n-1\right)-1\right)^{2}+4}+\sqrt{\left(4\left(3n\right)-1\right)^{2}+4}\right)>\sum_{n=1}^{k}\sqrt{36+\left(36n-15\right)^{2}}
$$
が成り立つことと同値である.したがって,$\sqrt{\left(12n-9\right)^{2}+4}+\sqrt{\left(12n-5\right)^{2}+4}+\sqrt{\left(12n-1\right)^{2}+4}>3\sqrt{\left(12n-5\right)^{2}+4}$を示せば十分である.図11においても$左辺>右辺$の証明と同様に考えると
$(中辺)=|DG|+|GJ|+|JM|+|MP|+|PS|+|SV|$,$(右辺)=|DV|$
となって,三角不等式より$中辺 > 右辺$が示された.
したがって,題意は示された.
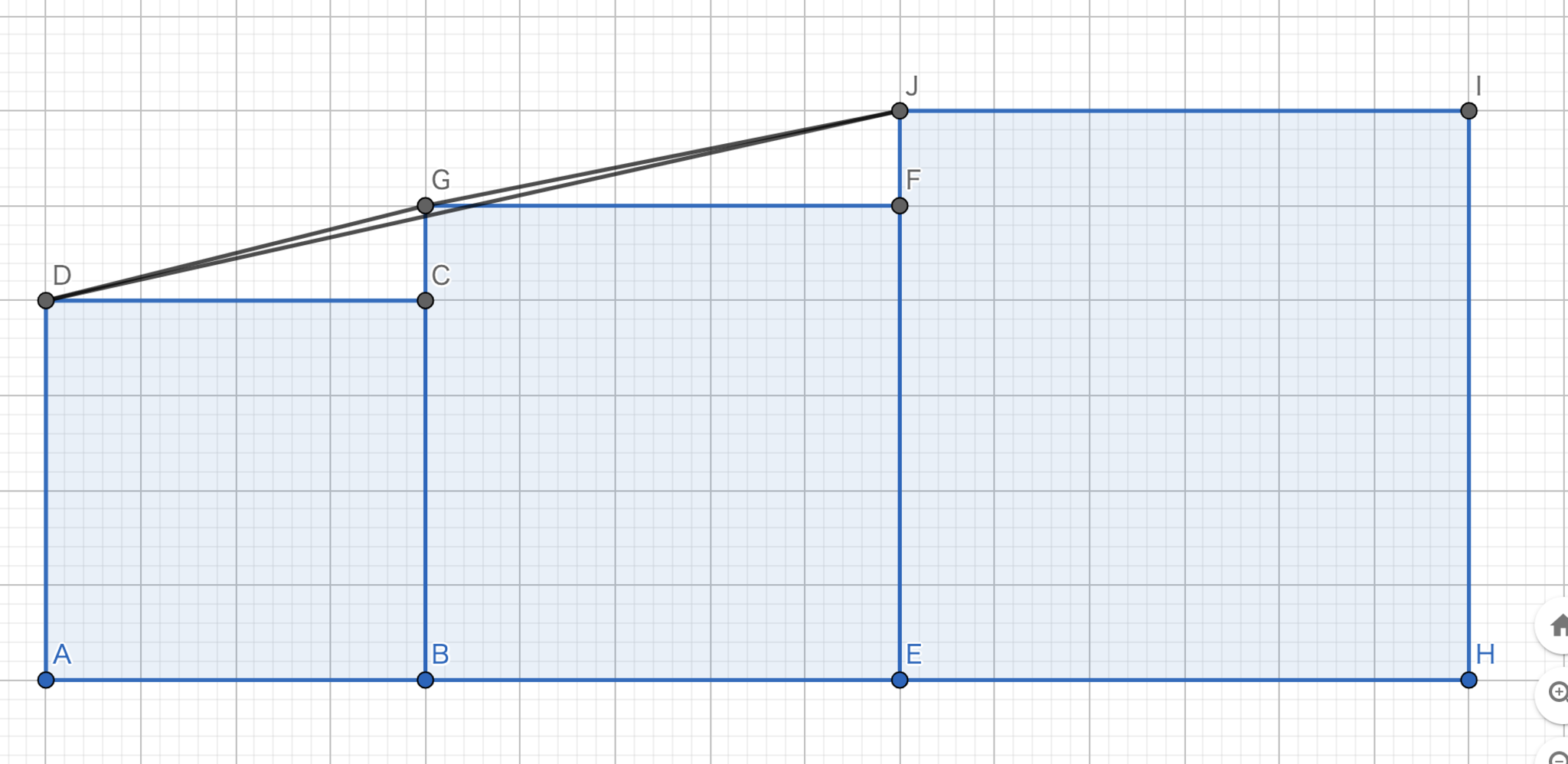問題4の不等式-解答用
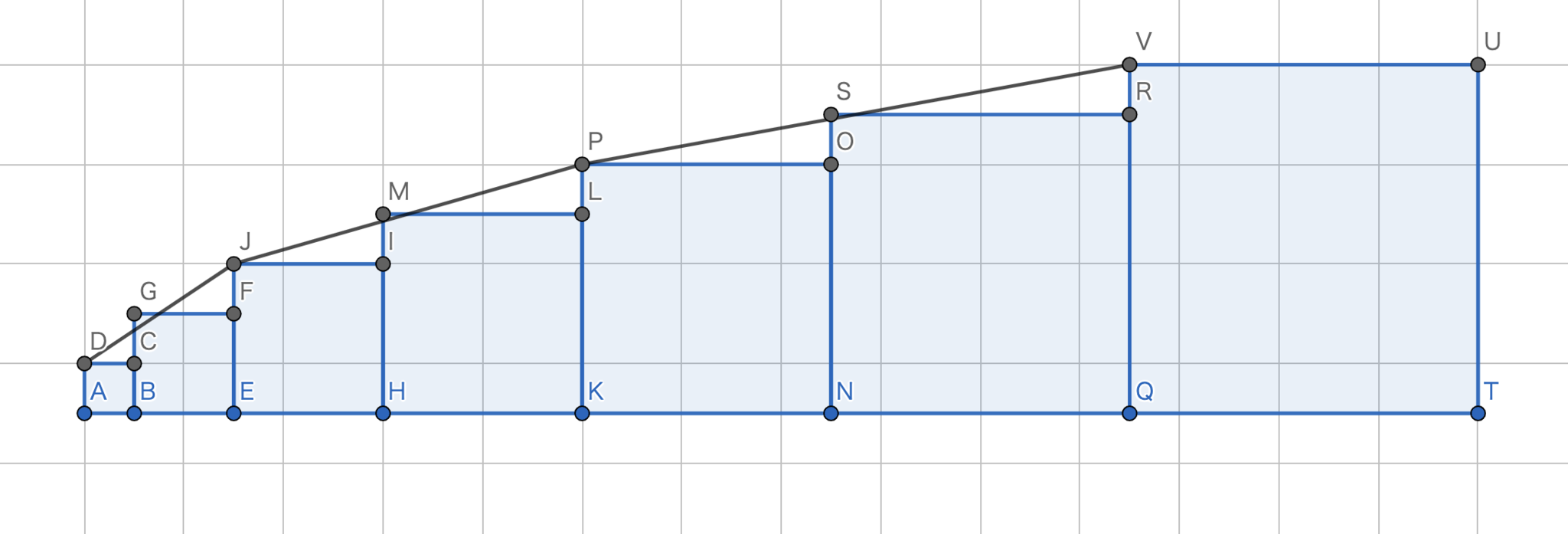問題4の不等式-解答用
このように,幾何的に考察することでほぼ自明に不等式が示せるケースがあります.仮に今回のケースを代数的にゴリ押すとどうなるのか見てみましょう.※1
$左辺>中辺$が成り立つことは
$$
\begin{align}
\sum_{n=1}^{3k}\left(\sqrt{\left(2n-1\right)^{2}+1}+\sqrt{\left(2n\right)^{2}+1}\right)>\sum_{n=1}^{3k}\sqrt{\left(4n-1\right)^{2}+4}
\end{align}
$$
が成り立つことと同値である.したがって,$\sqrt{\left(2n-1\right)^{2}+1}+\sqrt{\left(2n\right)^{2}+1}>\sqrt{\left(4n-1\right)^{2}+4}$を示せば十分である.
$$
\ \ \ \ \ \ \ \sqrt{\left(2n-1\right)^{2}+1}+\sqrt{\left(2n\right)^{2}+1}>\sqrt{\left(4n-1\right)^{2}+4} \\ \Longleftrightarrow \left(\left(2n-1\right)^{2}+1\right)+2\sqrt{\left(\left(2n-1\right)^{2}+1\right)\left(\left(2n\right)^{2}+1\right)}+\left(\left(2n\right)^{2}+1\right)>\left(4n-1\right)^{2}+4 \\
\Longleftrightarrow\sqrt{\left(\left(2n-1\right)^{2}+1\right)\left(\left(2n\right)^{2}+1\right)}>4n^{2}-2n+1 \\
\Longleftrightarrow\left(\left(2n-1\right)^{2}+1\right)\left(\left(2n\right)^{2}+1\right)>\left(4n^{2}-2k+1\right)^{2} \\
\Longleftrightarrow16n^{4}-16n^{3}+12n^{2}-4n+2>16n^{4}-16n^{3}+12n^{2}-4n+1 \\
\Longleftrightarrow 2>1
$$
より,$2>1$は明らかに成立するので$左辺 > 中辺$が示された.
$ $
$中辺 > 右辺$が成り立つことは
$$
\sum_{n=1}^{k}\left(\sqrt{\left(4\left(3n-2\right)-1\right)^{2}+4}+\sqrt{\left(4\left(3n-1\right)-1\right)^{2}+4}+\sqrt{\left(4\left(3n\right)-1\right)^{2}+4}\right)>\sum_{n=1}^{k}\sqrt{36+\left(36n-15\right)^{2}}
$$
が成り立つことと同値である.したがって,$\sqrt{\left(4\left(3n-2\right)-1\right)^{2}+4}+\sqrt{\left(4\left(3n-1\right)-1\right)^{2}+4}+\sqrt{\left(4\left(3n\right)-1\right)^{2}+4}>\sqrt{36+\left(36n-15\right)^{2}}$を示せば十分である.
$$
\ \ \ \ \ \ \ \sqrt{\left(4\left(3n-2\right)-1\right)^{2}+4}+\sqrt{\left(4\left(3n-1\right)-1\right)^{2}+4}+\sqrt{\left(4\left(3n\right)-1\right)^{2}+4}>\sqrt{36+\left(36n-15\right)^{2}} \\
\Longleftrightarrow\sqrt{\left(12n-9\right)^{2}+4}+\sqrt{\left(12n-5\right)^{2}+4}+\sqrt{\left(12n-1\right)^{2}+4}>3\sqrt{\left(12n-5\right)^{2}+4} \\
\Longleftrightarrow\sqrt{\left(12n-9\right)^{2}+4}+\sqrt{\left(12n-1\right)^{2}+4}>2\sqrt{\left(12n-5\right)^{2}+4} \\
\Longleftrightarrow\left(\left(12n-9\right)^{2}+4\right)+2\sqrt{\left(\left(12n-9\right)^{2}+4\right)\left(\left(12n-1\right)^{2}+4\right)}+\left(\left(12n-1\right)^{2}+4\right)>4\left(\left(12n-5\right)^{2}+4\right) \\
\Longleftrightarrow\sqrt{\left(144n^{2}-216n+85\right)\left(144n^{2}-24n+5\right)}>144n^{2}-120n+13 \\
\Longleftrightarrow144^{2}n^{4}-240\cdot144n^{3}+126\cdot144n^{2}-120\cdot26n+425>144^{2}n^{4}-240\cdot144n^{3}+126\cdot144n^{2}-120\cdot26n+169\\
\Longleftrightarrow 425>169
$$
より,$425>169$は明らかに成立するから$中辺 > 右辺$が示された.
これより,$左辺 > 中辺 > 右辺$が示された.
この問題は特に幾何的解法を選択することで計算量が大幅に減らせる問題でしたね.
※1:この代数的解法は 翁さん に教えてもらったものです.
問題5
図12において,$A_{n}=(\frac{n\left(n-1\right)}{2},\frac{n\left(n+1\right)}{2}-1)$とすると,
$$
(左辺)=\sum_{n=1}^{k}\left|A_{n}A_{n+1}\right| \\
(右辺)=\left|A_{1}A_{k+1}\right|
$$
$k \geq 2$の時,三角不等式を繰り返し用いることによって$左辺 > 右辺$となる.$k=1$の時,$左辺 = 右辺$となる.したがって,題意は示された.
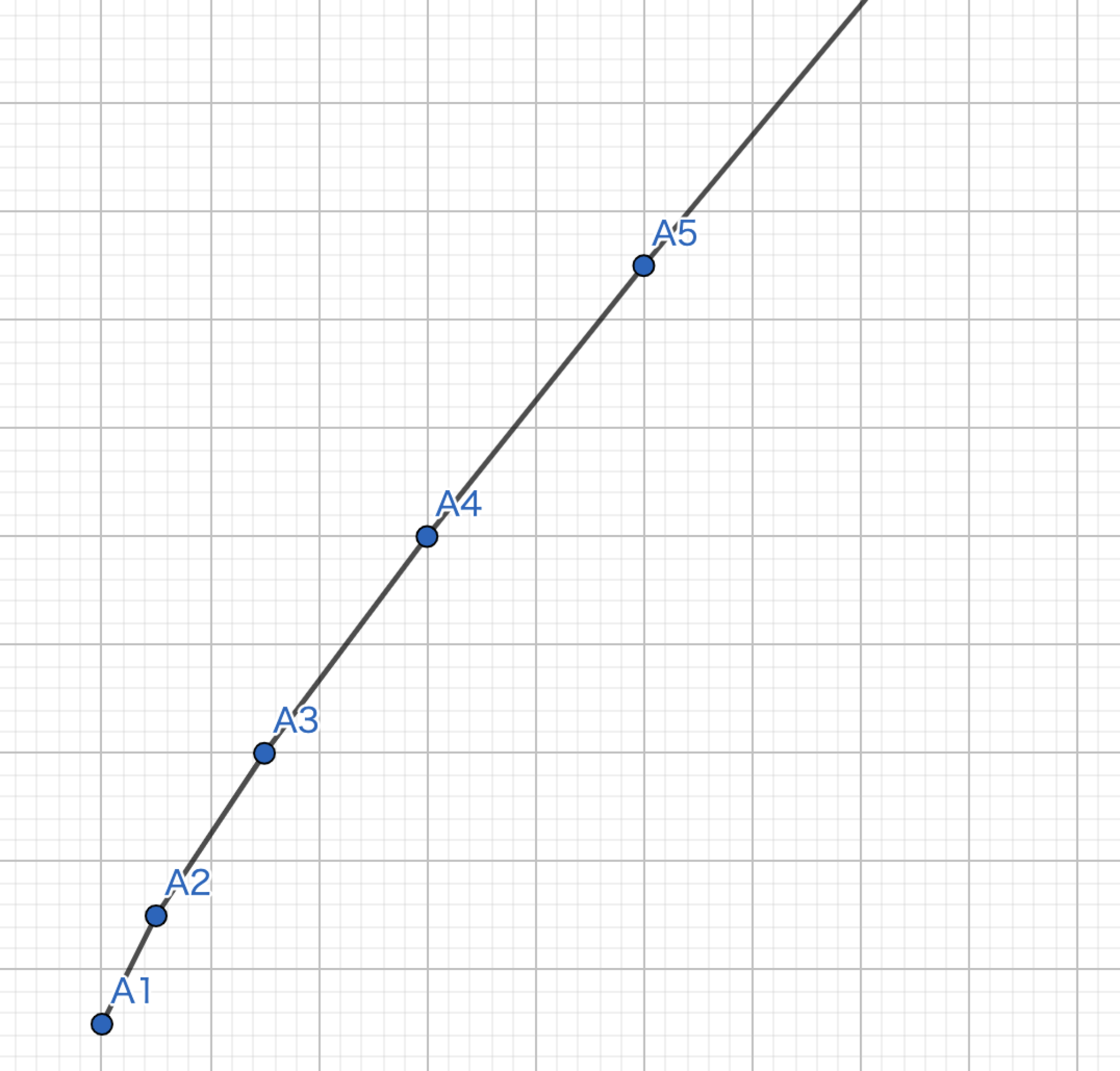問題5の不等式-解答用
5.おわりに
お疲れ様でした.長い記事でしたが見ていただきありがとうございました!私自身不等式に不慣れなところがあるので何かミス等発見したら指摘していただけると嬉しいです.
不等式の幾何的な考察は代数の観点で何も思いつかなかった時に試してみたり,あるいは計算量が減らせそうな時に使ってみてください!
