おきな杯の解説
はじめに
この記事では, 先日開催した おきな杯 の解説をしていきます. まだ問題を解いていなくて自力で解いてみたい方は、ぜひ上のリンクから問題を見ていってください. それでは参ります.
問題$1$
$AB\neq AC$をみたす三角形$ABC$において, その外接円を$Ω$とし, 角$BAC$の二等分線と$BC$の交点を$D, Ω$における点$A$を含む方の孤$BC$の中点を$E$とする. 直線$DE$と$Ω$の交点のうち$E$でない方を$F$としたとき, $Ω$における$A, F$の接線と$BC$の三直線が一点で交わることを示せ.
図を描いてみると次のようになります.
![問題!FORMULA[17][36151][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220527085010.jpeg?alt=media) 問題$1$
問題$1$
$\Omega$と$AD$の交点のうち$A$でない方を$G$とすると, $G$は$A$を含まない方の孤$BC$の中点です. つまり, 孤の中点を通る直線が$2$本あるわけです. ここで, 円と孤の中点に関するような構図があったなあと連想できれば方針が見えてきます.
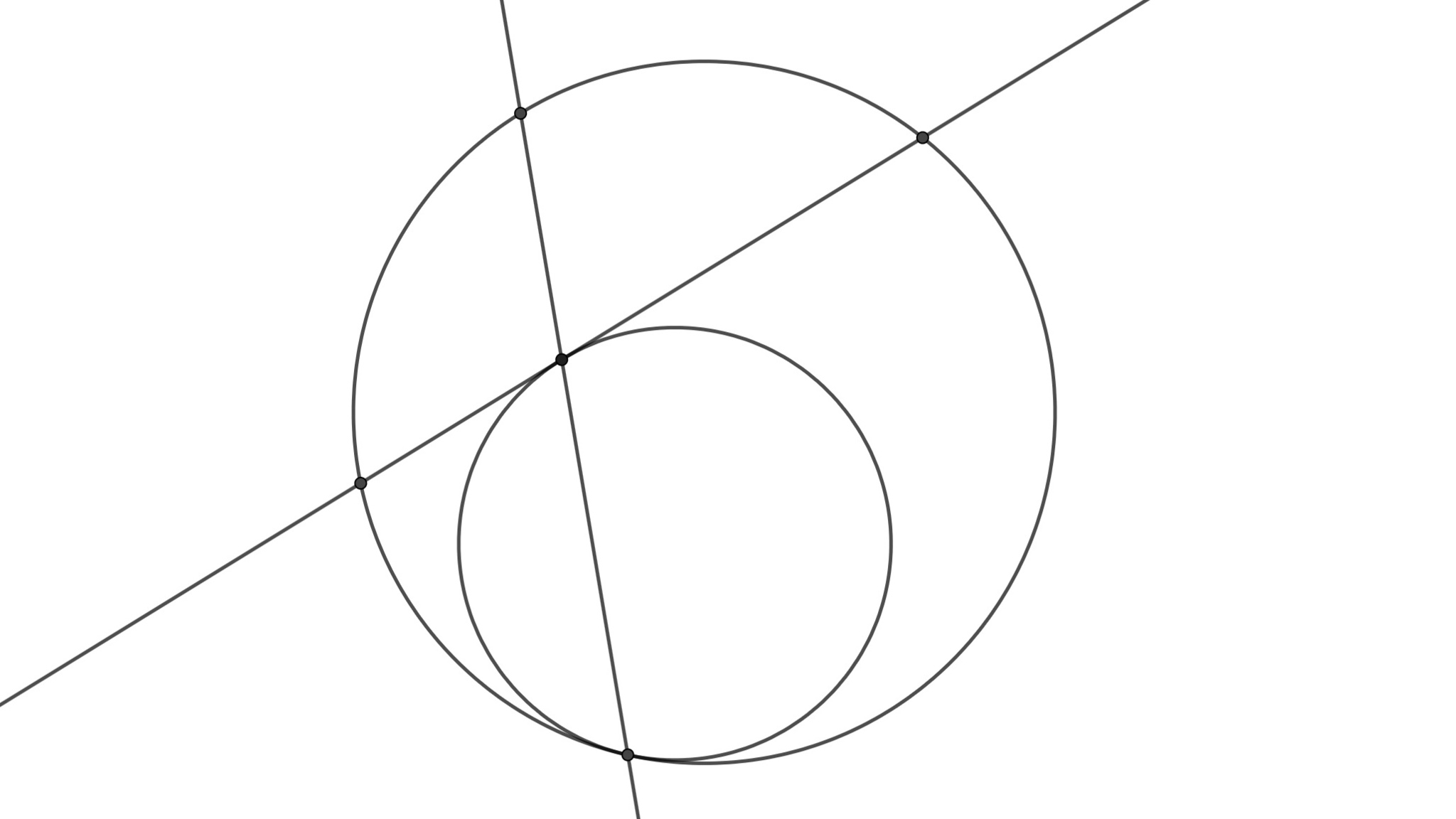 こんな構図があったなあ
こんな構図があったなあ
問題$1$の解説
$\Omega$と$AD$の交点のうち$A$でない方を$G$とし, 円$\Omega$を$A$を中心として$\cfrac{AD}{AG}$倍相似拡大した円を$\omega_1$としたとき, $\omega_1$は$A$で$\Omega$に内接する. また$G$は$A$を含まない方の孤$BC$の中点であるので, $\Omega$の$G$における接線がこの相似拡大により直線$BC$にうつることから$\omega_1$は$D$で$BC$と接する. 円$\Omega$を$F$を中心として$\cfrac{FD}{FE}$倍相似拡大した円を$\omega_2$としたとき, 同様に$\omega_2$は$F$で$\Omega$と内接し, $D$で$BC$と接する. よって三円$\Omega, \omega_1, \omega_2$の根心を考えれば, $AB\neq AC$より三円の中心は一直線上に並ばないので, $\Omega$における$A, F$の接線, $BC$の三直線が一点で交わることがわかる.
問題$2$
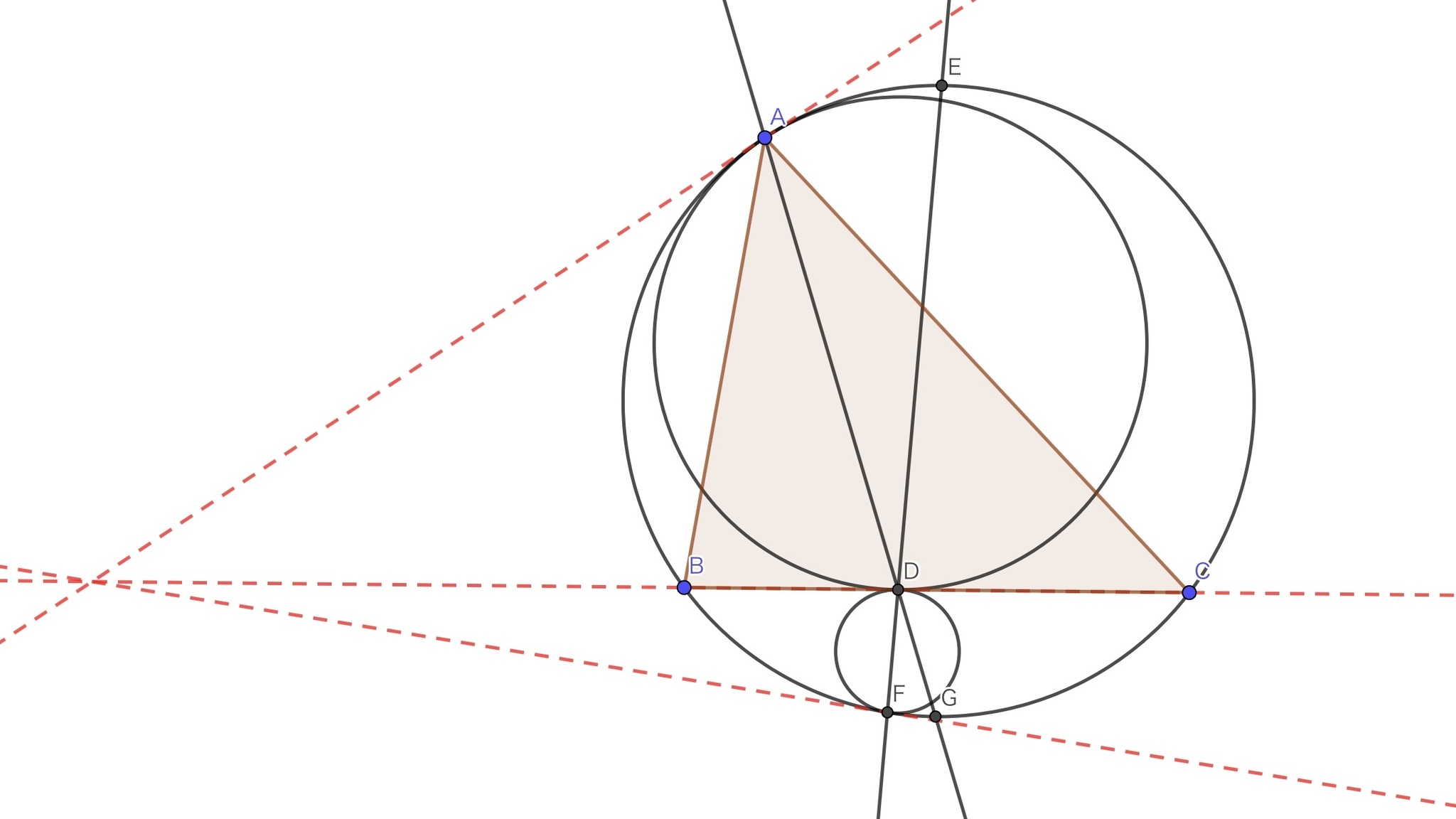
三角形$ABC$において,$ B, C$から対辺に下ろした垂線の足をそれぞれ$E, F$とし, $A$を通って$B$で$BE$に接する円を$Γ_1, A$を通って$C$で$CF$に接する円を$Γ_2$とする. 三角形$ACF$の外接円と$Γ_1$の交点のうち$A$でない方を$P$, 三角形$ABE$の外接円と$Γ_2$の交点のうち$A$でない方を$Q$とし, $ABC$の外心$O$と$BC$に関して対称な点を$O’$としたとき,$ AO’ ,BP ,CQ$が一点で交わることを示せ.
図を描いてみると次のようになります.
![問題!FORMULA[85][36182][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220527140523.jpeg?alt=media) 問題$2$
問題$2$
ややこしい…
とりあえずこの図でangle-chaseをしてみます. $H$を垂心とすると,
\begin{align}
\angle HBP
&=\angle BAP\\
&=\angle FAP\\
&=\angle FCP\\
&=\angle HCP
\end{align}
おっ!$P, B, C, H$の共円がわかりました. この調子で考えていけば案外なんとかなりそうですね.
問題$2$の解説
相異なる三点$X, Y, Z$に対して, 直線$XY$を$X$を中心に反時計回りに角度$\theta$だけ回転させたときに直線$XZ$に一致するとき, この$\theta$を$\measuredangle YXZ$で表す. ただし, $180^\circ $の差は無視して考える.
三角形$ABC$の垂心を$H$としたとき,
\begin{align}
\measuredangle HBP
&=\measuredangle BAP\\
&=\measuredangle FAP\\
&=\measuredangle FCP\\
&=\measuredangle HCP\\
\end{align}
より$P, B, C, H$の共円を得る. 同様に$Q, B, C, H$の共円も得るので, $P, Q, B, C, H$の共円を得る.
以下では$\Gamma_1$と$\Gamma_2$が相異なる二点で交わるときを考える. この二円が接するときも以下とほぼ同様にして考えられる.
$\Gamma_1$と$\Gamma_2$の交点のうち$A$でない方を$K$とすると, $H$と$O$が等角共役の関係にあることから
\begin{align}
\measuredangle BKC
&=\measuredangle BKA+\measuredangle AKC\\
&=\measuredangle EBA+\measuredangle ACF\\
&=\measuredangle CBO+\measuredangle OCB\\
&=\measuredangle COB\\
&=\measuredangle BO'C
\end{align}
より, $K, O', B, C$は共円である.
\begin{align}
\measuredangle BKA
&=\measuredangle EBA\\
&=\measuredangle ACF\\
&=\measuredangle AKC\\
\end{align}
より$AK$は角$BKC$の二等分線であるから, $O'$が三角形$KBC$の外接円における$K$を含まない方の孤$BC$の中点であることと合わせて, $K, A, O'$が一直線上に並ぶことを得る. 以上より, 三角形$HBC$の外接円, $\Gamma_1, \Gamma_2$の三円の根心を考えれば$AO', BP, CQ$が一点で交わることが示される.
問題$3$
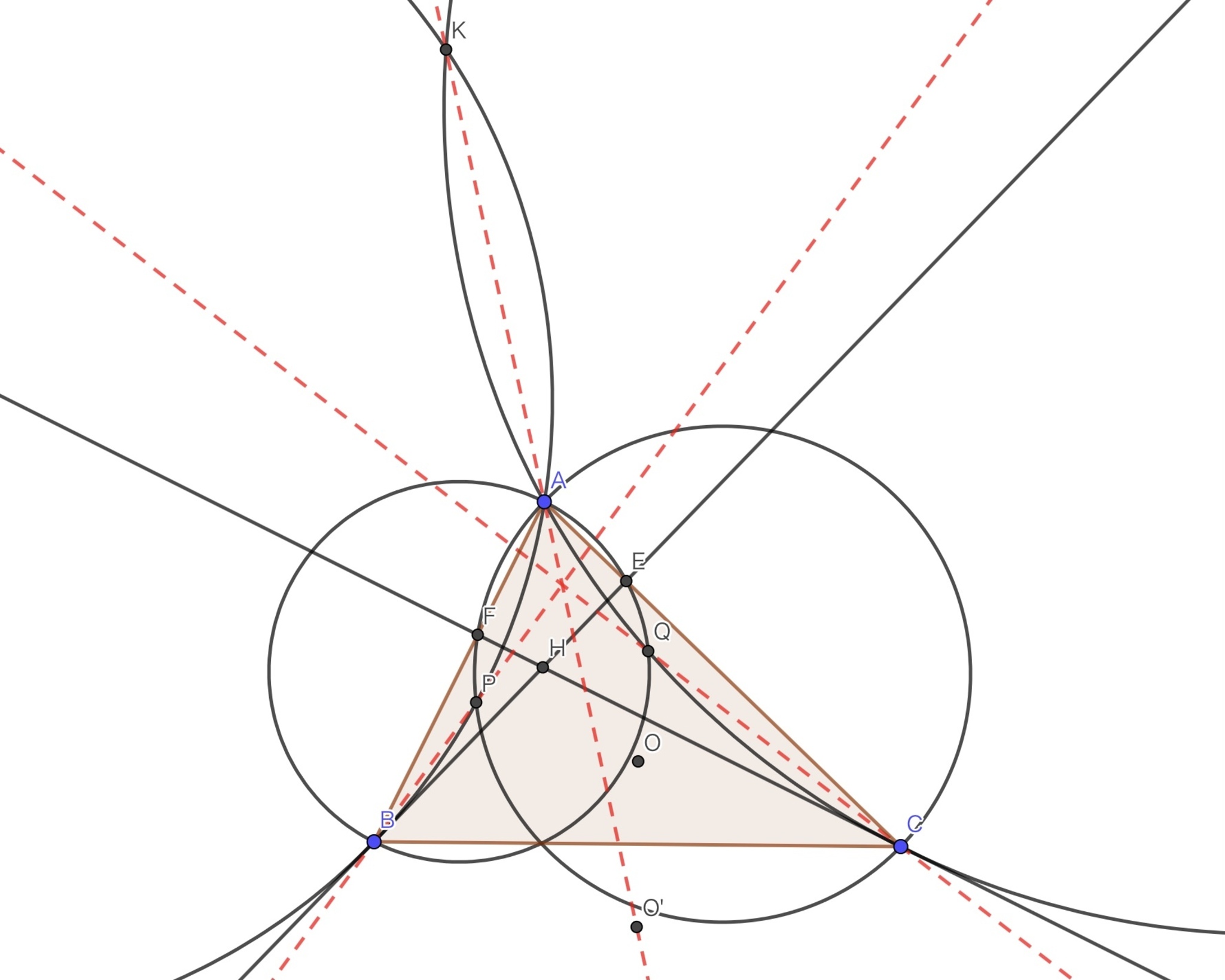
三角形$ABC$において, 内心を$I$, 角$A$内の傍心を$J, A$から$BC$に下ろした垂線の足を$D$とし,$ BC$に関して$I$と対称な点を$I’$としたとき, $D, I’, J$が同一直線上にあることを示せ.
図を描いてみると次のようになります.
![問題!FORMULA[136][36213][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220529225935.jpeg?alt=media) 問題$3$
問題$3$
$AD, II'$はどちらも$BC$に垂直よりこの二直線は平行なので, 三角形$JII'$と三角形$JAD$の相似がわかれば良さそうです.
問題$3$の解説
$AB=AC$のときは$BC$の垂直二等分線上にこの三点が並ぶので, 以下そうでないときを考える.
三角形$ABC$の内接円と$BC$との接点を$E$とし, $ES$が三角形$ABC$の内接円の直径となるように$S$をとり, 三角形$ABC$の傍接円のうち$J$を中心とするものと$BC$との接点を$T$とする. $A$を中心とし三角形$ABC$の内接円を角$A$内の傍接円にうつすような相似拡大を考えたときに, $S$は$T$に, $I$は$J$にそれぞれうつるから$A, S, T$と$A, I ,J$はそれぞれ一直線上に並び, $AD, SI', JT$の平行から$\angle JII'=\angle JAD$,
\begin{align}
JI:JA
&=TS:TA\\
&=SE:AD\\
&=II':AD\\
\end{align}
より三角形$JII'$と三角形$JAD$の相似がわかるので題意は示された.
問題$4$
$AB\neq AC$をみたす三角形$ABC$において, 線分$AB, AC$の垂直二等分線と直線$AC, AB$との交点をそれぞれ$D,E$とし,$ AB, AC$の中点をそれぞれ$M,N$とする. また, 三角形$ABC$の外接円における$A$での接線と$BC$との交点を$P$とし, 三角形$ABC$の外心を$O$とする. $MN$と$DE$の交点を$Q$としたとき, $O, P, Q$が同一直線上にあることを示せ.
図を描いてみると次のようになります.
![問題!FORMULA[186][36244][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220531102526.jpeg?alt=media) 問題$4$
問題$4$
$DM\perp ME, DN\perp NE$より$D, E, M, N$は共円です. ここで$ME$と$ND$の交点が$A$, $MD$と$NE$の交点が$O$, $MN$と$DE$の交点が$Q$なので, $DE$の中点(つまり, $D, E, M, N$の乗る円の中心)を$K$とすると, Brokardの定理より$AK\perp OQ$がわかります. したがって$AK\perp OP$を示せばいいわけです. ここで$AP$は三角形$ABC$の外接円に$A$で接し, また$AK$は三角形$ABC$の$A$における類似中線なので, 問題$1$と同様のとり方で$F$をとったときに, $P$の極線である$AF$が類似中線であることを示せばよさそうです.
問題$4$の解説
相異なる三点$X, Y, Z$に対して, 直線$XY$を$X$を中心に反時計回りに角度$\theta$だけ回転させたときに直線$XZ$に一致するとき, この$\theta$を$\measuredangle YXZ$で表す. ただし, $180^\circ $の差は無視して考える.
$DM\perp ME, DN\perp NE$より, 四点の位置関係にかかわらず$D, E, M, N$は共円である. $ME$と$ND$の交点が$A$, $MD$と$NE$の交点が$O$, $MN$と$DE$の交点が$Q$であるから, $D, E, M, N$の乗る円の中心, すなわち$DE$の中点を$K$とすると, Brokardの定理より$AK\perp OQ$を得る.
$BC$の中点を$L$とすると, $\measuredangle LAC=\measuredangle BAK$
$DA=DB, EA=EC$より
\begin{align}
\measuredangle DBE
&=\measuredangle DBA\\
&=\measuredangle BAD\\
&=\measuredangle EAC\\
&=\measuredangle ACE\\
&=\measuredangle DCE\\
\end{align}
から$B, C, D, E$の共円がわかるから, 三角形$ABC$と三角形$ADE$の相似がわかり, 三角形$ACL$と三角形$AEK$の相似もわかるので$\measuredangle LAC=\measuredangle EAK$, すなわち$\measuredangle LAC=\angle BAK$を得る.
以下三角形$ABC$の外接円を$\Gamma$とする.
角$BAC$の二等分線と$BC$の交点を$S$, $\Gamma$における点$A$を含む方の弧$BC$の中点を$T$, $\Gamma$における点$A$を含まない方の弧$BC$の中点を$U$, $ST$と$\Gamma$との交点のうち$T$でない方を$V$としたとき, $\measuredangle LAC=\measuredangle BAV$
$T, L, U$は線分$BC$の垂直二等分線上にあり, 特に$TU$は$\Gamma$の直径であるので, $A, S, U$は一直線上に並ぶことから$TA\perp AS, TL\perp LS$を得る. したがって四点の位置関係によらず$A, L, S, T$は共円であり,
\begin{align}
\measuredangle VAU
&=\measuredangle VTU\\
&=\measuredangle STL\\
&=\measuredangle SAL\\
\end{align}
であるので, これと$AU$が角$BAC$を二等分することをあわせて$\measuredangle LAC=\measuredangle BAV$を得る.
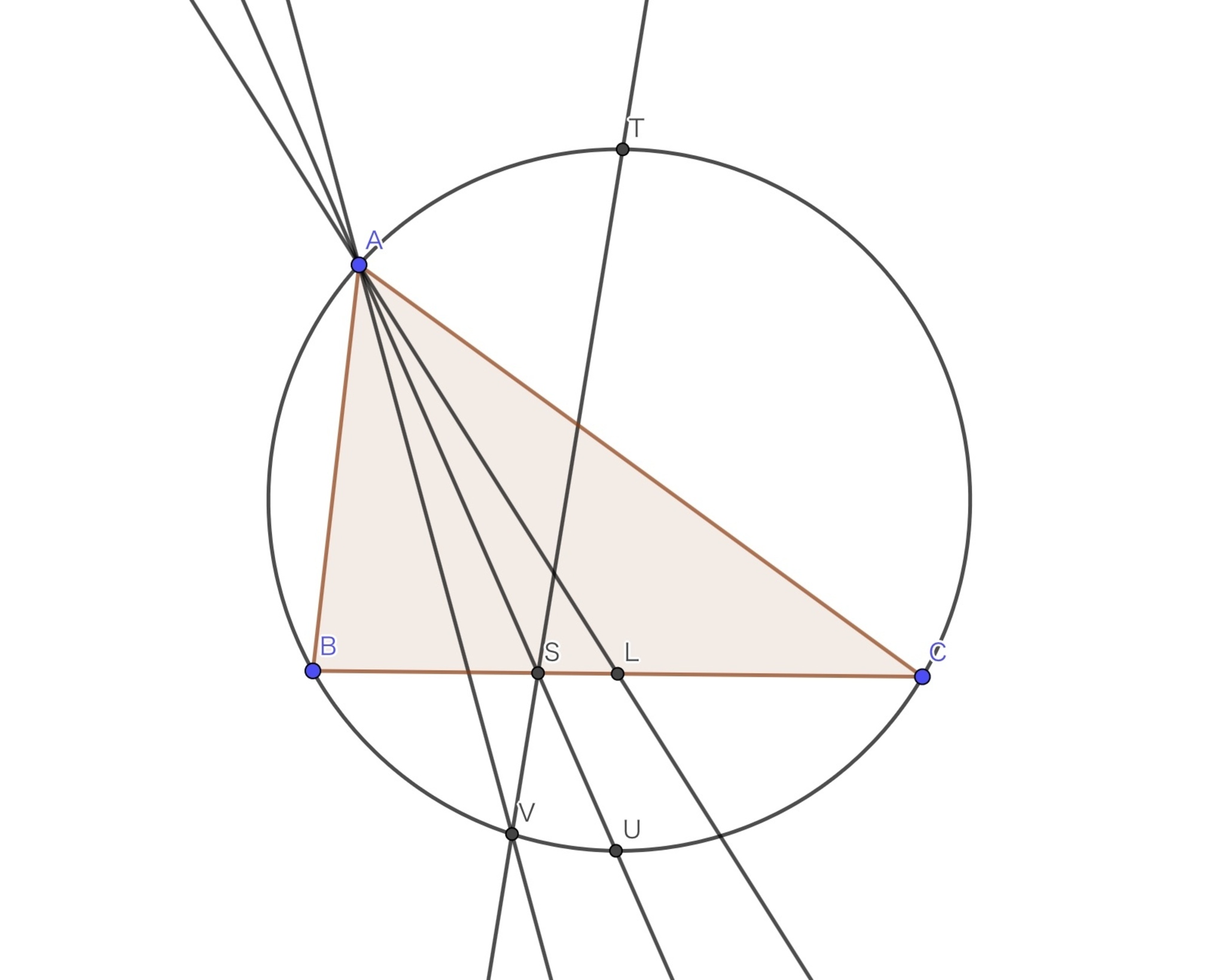
補題$1, 2$より$\measuredangle BAK=\measuredangle BAV$から$A, K, V$は一直線上に並ぶ. ここで問題$1$より$PV$が$V$で$\Gamma$に接することから$VA$, つまり$KA$が$P$の$\Gamma$に関する極線であることがわかるので, $AK\perp OP$が得られる. これと$AK\perp OQ$を合わせて, $O, P, Q$が同一直線上にあることが示された.
問題$5$
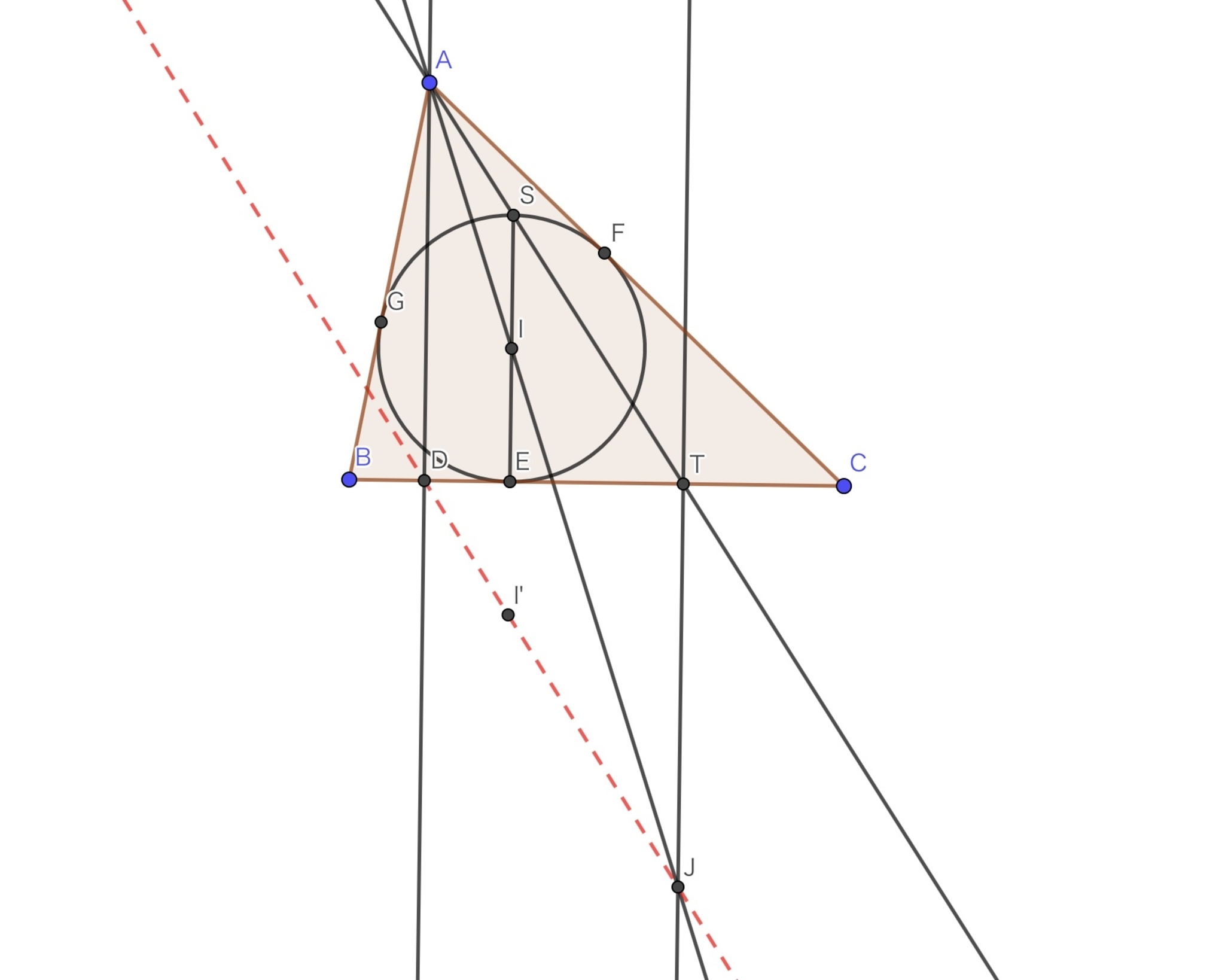
$AB\neq AC$をみたす三角形$ABC$において, その外接円を$Ω$とし, $A$を通って$BC$に垂直な直線と$Ω$の交点のうち$A$でない方を$D$とする. $B, C$から対辺に下ろした垂線の足をそれぞれ$E, F$とし, 三角形$DEF$の外接円と$Ω$の交点のうち$D$でない方を$P, PE$と$Ω$の交点のうち$P$でない方を$Q$としたとき, $AD, BQ, EF$が一点で交わることを示せ.
図を描いてみると次のようになります.
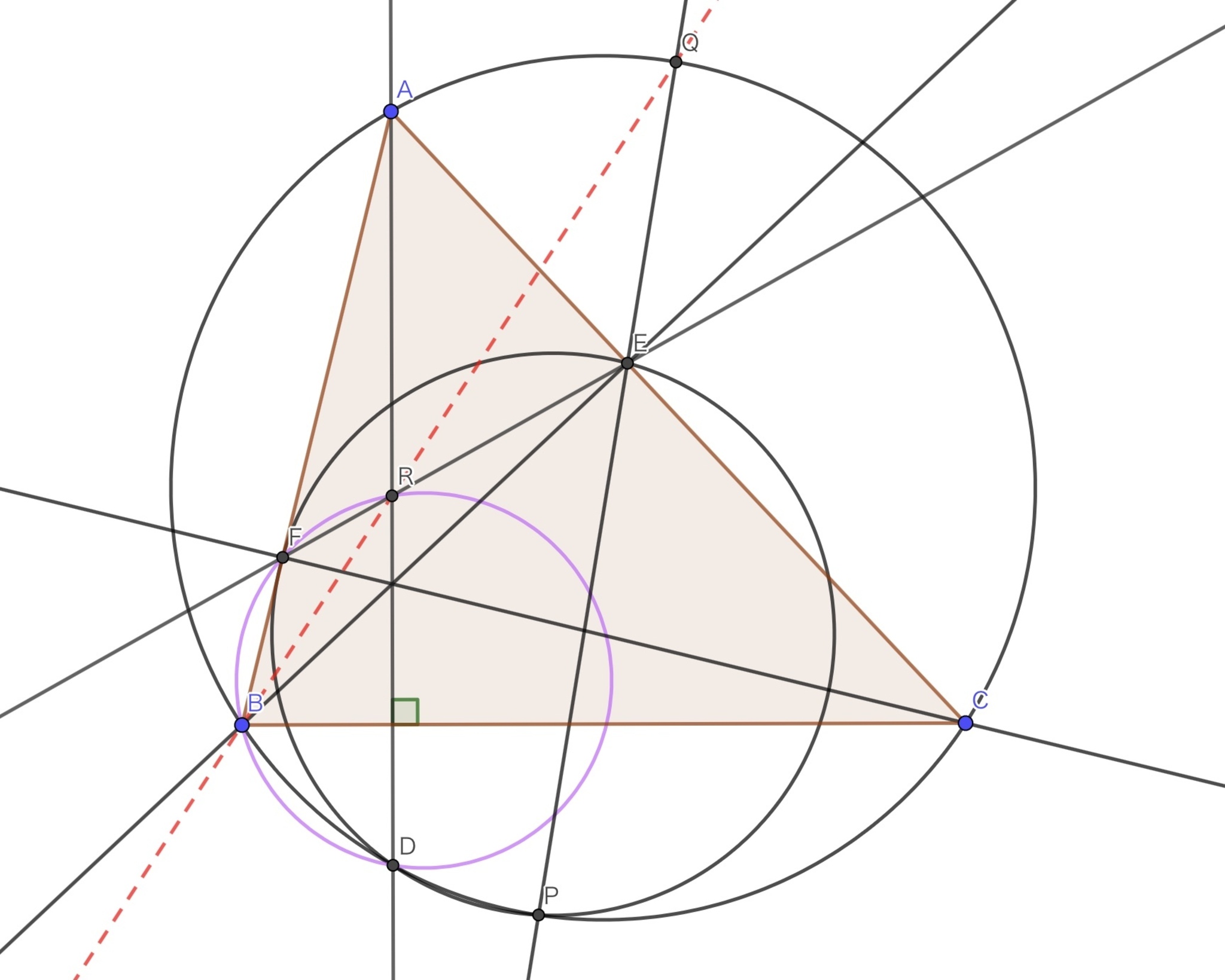
![問題!FORMULA[311][36275][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220531090538.jpeg?alt=media) 問題$5$
問題$5$
うーむ. とりあえず$AD$と$EF$の交点を$R$として, $B, Q, R$が一直線上にあることを示しましょう. この図でangle-chaseをしてみると,
\begin{align}
\angle AFR
&=\angle AFE\\
&=\angle ACB\\
&=\angle ADB\\
&=\angle RDB
\end{align}
より$B, D, F, R$は共円です. よって
\begin{align}
\angle RBD
&=\angle RFD\\
&=\angle EFD\\
&=180^\circ -\angle EPD\\
&=180^\circ -\angle QPD\\
&=\angle QBD\\
\end{align}
より$B, Q, R$が一直線上にあることがわかりました.
あれ??解けちゃった…
問題$5$の解説
相異なる三点$X, Y, Z$に対して, 直線$XY$を$X$を中心に反時計回りに角度$\theta$だけ回転させたときに直線$XZ$に一致するとき, この$\theta$を$\measuredangle YXZ$で表す. ただし, $180^\circ $の差は無視して考える. $AD$と$EF$の交点を$R$としたとき, $B, C, E, F$の共円から
\begin{align}
\measuredangle RFB
&=\measuredangle EFA\\
&=\measuredangle ACB\\
&=\measuredangle ADB\\
&=\measuredangle RDB\\
\end{align}
より$B, D, F, R$の共円を得る. よって
\begin{align}
\measuredangle DBR
&=\measuredangle DFR\\
&=\measuredangle DFE\\
&=\measuredangle DPE\\
&=\measuredangle DPQ\\
&=\measuredangle DBQ
\end{align}
より$B, Q, R$は一直線上にあるので, 題意は示された.
おわりに
参加していってくれたみなさん, 本当にありがとうございました!!急いで書き上げたので不備があったら教えてくれると嬉しいです.
