多重総和記号を組み合わせ論的に考察する
目次
- はじめに
- 問題
- 拡張
- 別解(2022/06/25追記)
- おわりに
1.はじめに
今回は通常では計算することができないような多重総和記号の式を組み合わせ論的に見ることで簡単に解く方法を皆さんにお伝えしていきたいと思います.必要な前提知識はほぼゼロです.
2.問題
以下の式を計算せよ.
シンプルな式ではありますが,地味に手が付けにくい問題です.こういった多重総和記号の式はお互いのシグマが絡み合っているので機械的に解く方法がありません.したがって,これほどにシンプルな問題も十分難しいのです.さらにただ単純に「組み合わせ論的に見る」というポイントだけではこの問題は解けません.これもこの問題を難しくしている要因でしょう.では,早速解いていきましょう!!
解説
$$f_{j}\left(i\right)=\sum_{a_{1}=1}^{i}\sum_{a_{2}=1}^{a_{1}}\cdots\sum_{a_{j}=1}^{a_{j-1}}a_{j}$$
便宜上,上記のように$f_{j}(i)$を定義します.また,$f_{1}(i)=\sum_{a_{1}=1}^{i}a_{1}$とします.今回は$f_{15}(4)$を求めれば良いのですね.まずは,シグマのせいでこの式がどんな式なのかとてもわかりにくいです.一旦簡単な状況でシグマをバラしてみましょう.
$$ f_{1}(4)=1+2+3+4\\ f_{2}(4)=(1)+(1+2)+(1+2+3)+(1+2+3+4) \\ f_{3}(4)=\{(1)\}+\{(1)+(1+2)\}+\{(1)+(1+2)+(1+2+3)\}+\{(1)+(1+2)+(1+2+3)+(1+2+3+4)\} \\ $$
なんだか法則性がある式ですね.例えば上の例では,こんなことが言えそうです.
$$ f_{3}(4)=f_{3}(3)+f_{2}(4) $$
これは定義から考えれば同様のことが全ての$f$に対して言えそうです.したがって,以下の補題が成立します.
$2$以上の任意の正整数$i,j$に対して$f_{j}(i)=f_{j-1}(i)+f_{j}(i-1)$が成立する.
今回はこの補題を利用して解いていきます.ここで,表を考えてみましょう.
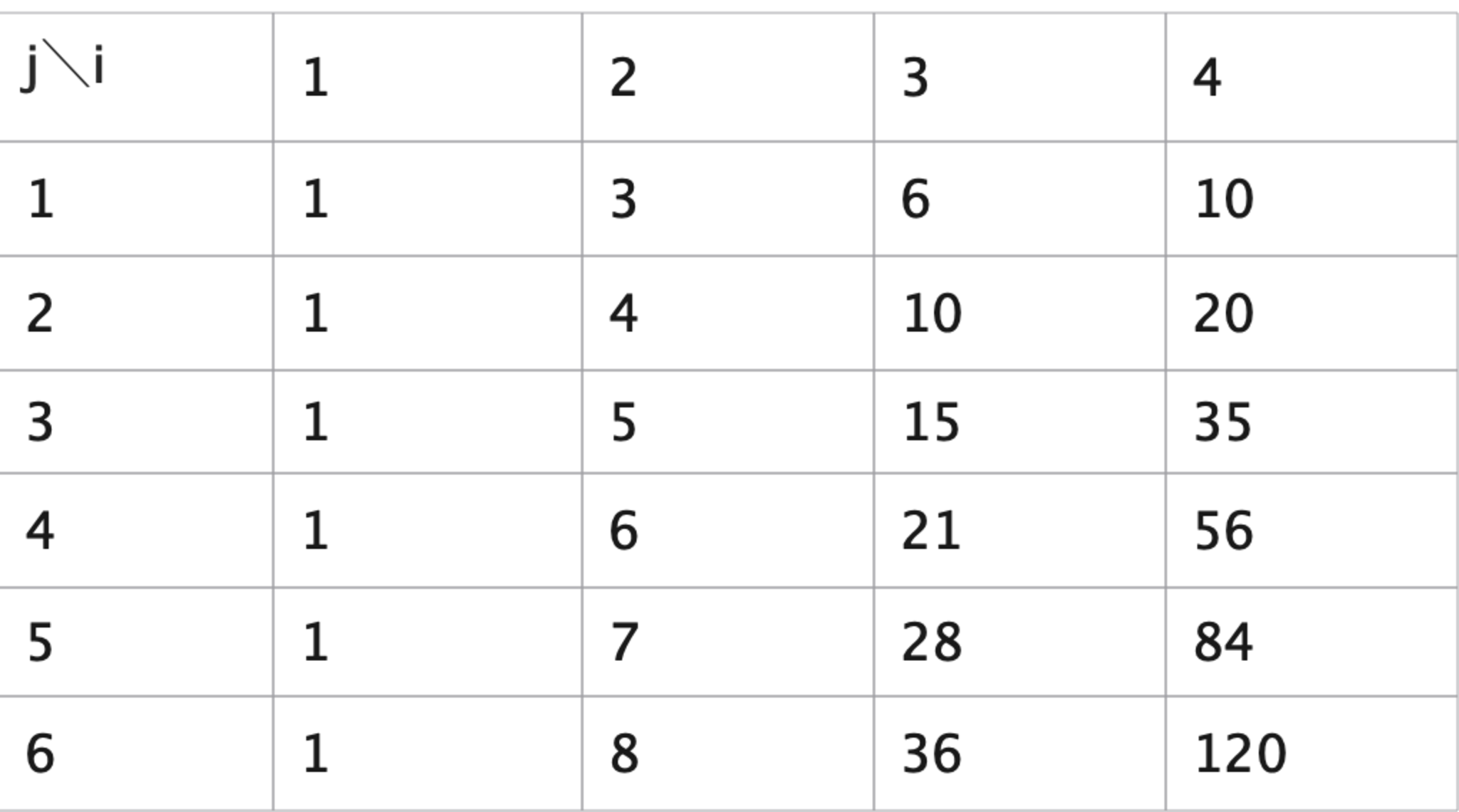(๑╹ω╹๑ )
任意の$j$に対して$f_{j}(1)=1$が成り立つことは容易にわかります.これと補題$1$を組み合わせて用いることで上のような表を書くことができます.表で言うと補題1は「あるマスの数はその左のマスと上のマスの和」と表現できます.さて,このような表に見覚えはありませんか?そうです.道順を数えるときに使うやつです!!
＜参考:道順の数え上げ＞
「下の図2において,地点Aから地点Bまで一度も引き返すことなく行く方法は何通りか？」
と言うような問題において頻出のテクニックです."ある地点に行く場合の数はその地点の下に行く場合の数と左に行く場合の数の和"という性質を利用してどんどん数字を書き込んで数え上げていく方法です.
これは主に$_{n}P_{r}, \ _{n}C_{r}$といった数え上げの記号を習っていない小学生が中学入試の際に使う手法として有名です.ですから,実際これらは$_7C_3=35$と計算することも可能です.
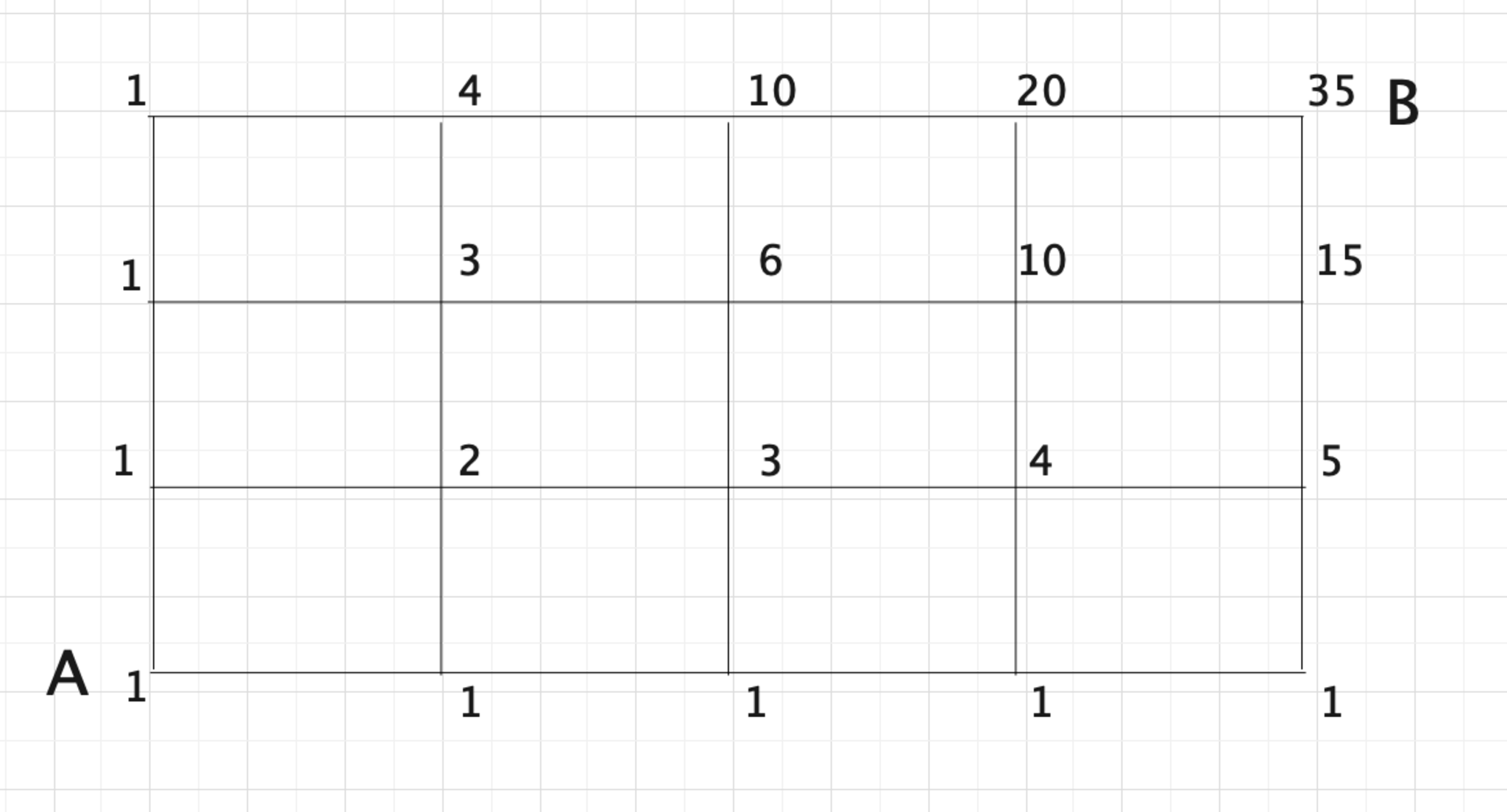中学受験で頻出のアレ
実は,図1の表はこの道順の数え上げと全く同じことをしているのです.図1の表に便宜上0行目と-1行目を追加すると見えやすいかと思います.
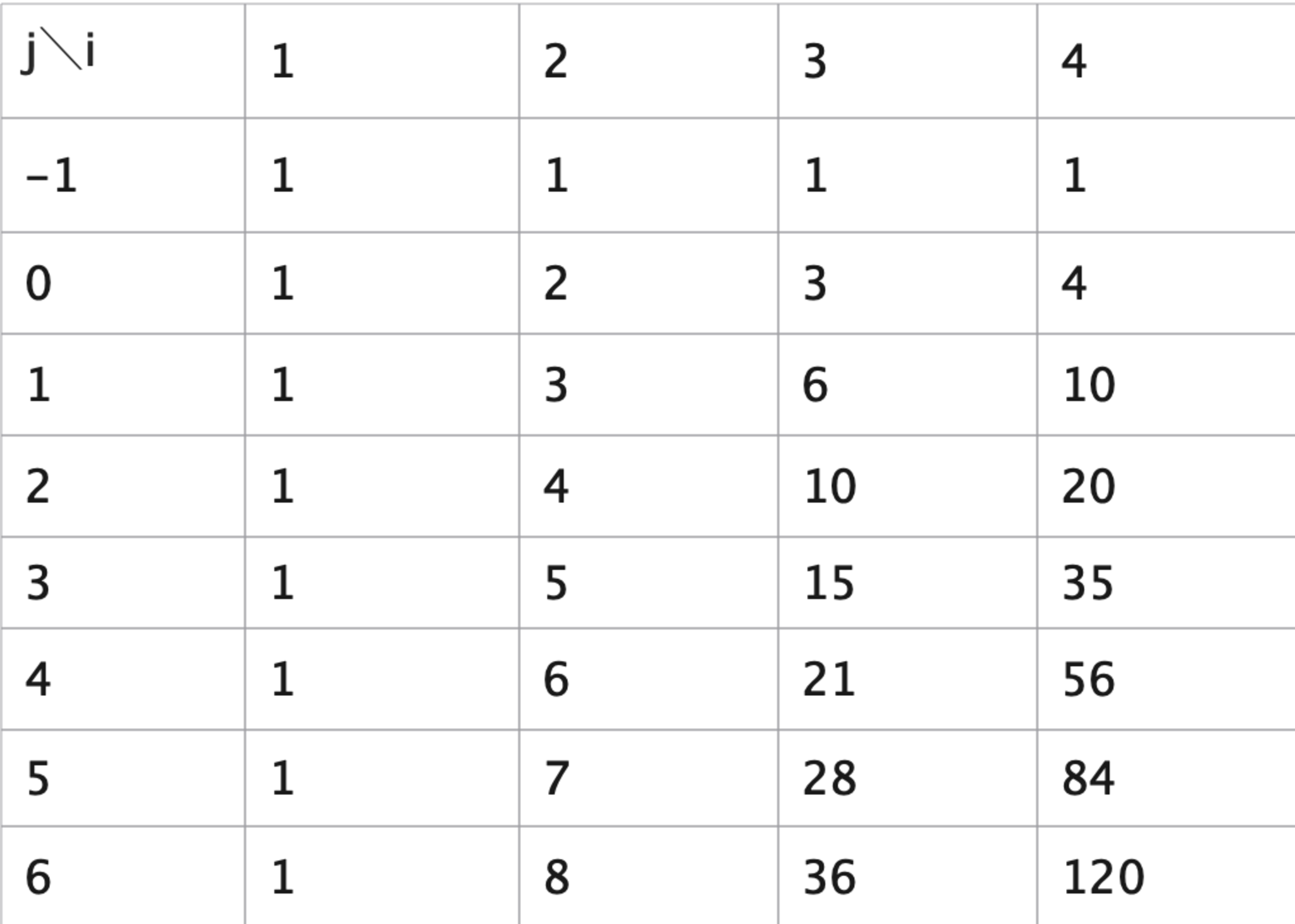0,-1行目を追加した図1の表
これより,$f_{j}(i)=_{(j+1)+(i-1)}C_{i-1}$であることがわかりますね.したがって今回求める$f_{4}(15)=_{19}C_{3}=969$となるわけです.
3.拡張
ほとんど「2.問題」で扱いましたが,今回の事実は一般の数に拡張することができますね。最後に公式のような形で表して終わりにしましょう.
任意の正整数$n,m$に対して以下が成立する.
定義より,
$$
\begin{align*}
\sum_{a_{1}=1}^{n-1}\sum_{a_{2}=1}^{a_{1}}\cdots\sum_{a_{m}=1}^{a_{m-1}}a_{m}=\sum_{a_{1}=1}^{n-1}\sum_{a_{2}=1}^{a_{1}}\cdots\sum_{a_{m}=1}^{a_{m-1}}a_{m}+\sum_{a_{1}=1}^{n}\sum_{a_{2}=1}^{a_{1}}\cdots\sum_{a_{m-1}=1}^{a_{m-2}}a_{m-1} \\
\end{align*}
$$
である.また,任意の正整数$k$に対し,$$\sum_{a_{1}=1}^{1}\sum_{a_{2}=1}^{a_{1}}\cdots\sum_{a_{k}=1}^{a_{k-1}}a_{k}=1$$
である.これらより,求める式は原点から$(n-1,m+1)$へ一度も引き返さずにいくような場合の数と等しい.したがって,$(与式)=_{n+m}C_{n-1}$である.題意は示された.
4.別解(2022/06/25追記)
二項係数で遊んでいたら別解を思いつきました.今回利用する公式は以下の通りです.
$$\sum_{n=k}^{m}{_{n}C_{k}=_{m+1}C_{k+1}}$$
これを繰り返し適用するとどうなるでしょうか？？以下ではとりあえず$k=1$として考えてみます.
$$\sum_{a_{1}=1}^{n}\sum_{a_{2}=1}^{a_{1}}\cdots\sum_{a_{m}=1}^{a_{m-1}}{_{a_{m}}C_{1}}=\sum_{a_{1}=1}^{n}\sum_{a_{2}=1}^{a_{1}}\cdots\sum_{a_{m-1}=1}^{a_{m-2}}{_{a_{m-1}+1}C_{2}}=\sum_{a_{1}=1}^{n}{_{n+m-1}C_{m}}=_{n+m}C_{m+1}=_{n+m}C_{n-1} $$
$n$という数字を二項係数を$_{n}C_{1}$と捉えることで目的の式を得ることができました.ただし$_{a}C_{b}$において,$a < b$であるときは$0$とします.
5.終わりに
今回の問題は組み合わせ論的に見ることで見通しよく計算できる問題でした.このような多重総和記号を含んだ計算をしなければならない場面が存在するのかわかりませんが,もしそのような機会があるなら使ってみてください!!(少なくとも僕は一度しか使ったことがありません.)
この記事は,新たに多重総和記号の計算法則が見つかれば随時追加していきたいと思います.一応,追加報告は twitter でしていきますのでもしよかったらチェックして行ってくださ〜い.拙く,長い記事でしたが最後まで見てくれてありがとうございました!!