フォロワー2800人突破記念問題の解答
はじめに
この記事では、先日私のTwitterアカウントのフォロワー数が2800人を突破したことを記念して作った問題の解説をします。
こんな問題です。
問題
フォロワー2800人突破記念問題!
— ａｐｕ (@apu_yokai) June 26, 2022
次のように図形を「成長」させることを考えます
・第１世代は単位正方形４つを合体した正方形
・第(n+1)世代は第n世代の角に３つの単位正方形を付け加える
ただし角とは図形の内角が90度となる頂点のこと
単位正方形の面積を１とすると、第３０世代の面積はいくつ? pic.twitter.com/t1coLQg02u
第１世代～第７世代
「どうせ答えが $2800$ になるんでしょ」と思いましたか?
……そのとおりです。答えは $2800$ です()
この記事ではそれを$4+1$ とおりの方法で求めてみたいと思います。
解答
解法1 がんばって数える
第30世代はこんな感じになります。
頑張って数えよう
世代数入り
大変そうに見えますが、対称性を使って正方形のカタマリごとに数えれば手作業でも数えることができます。
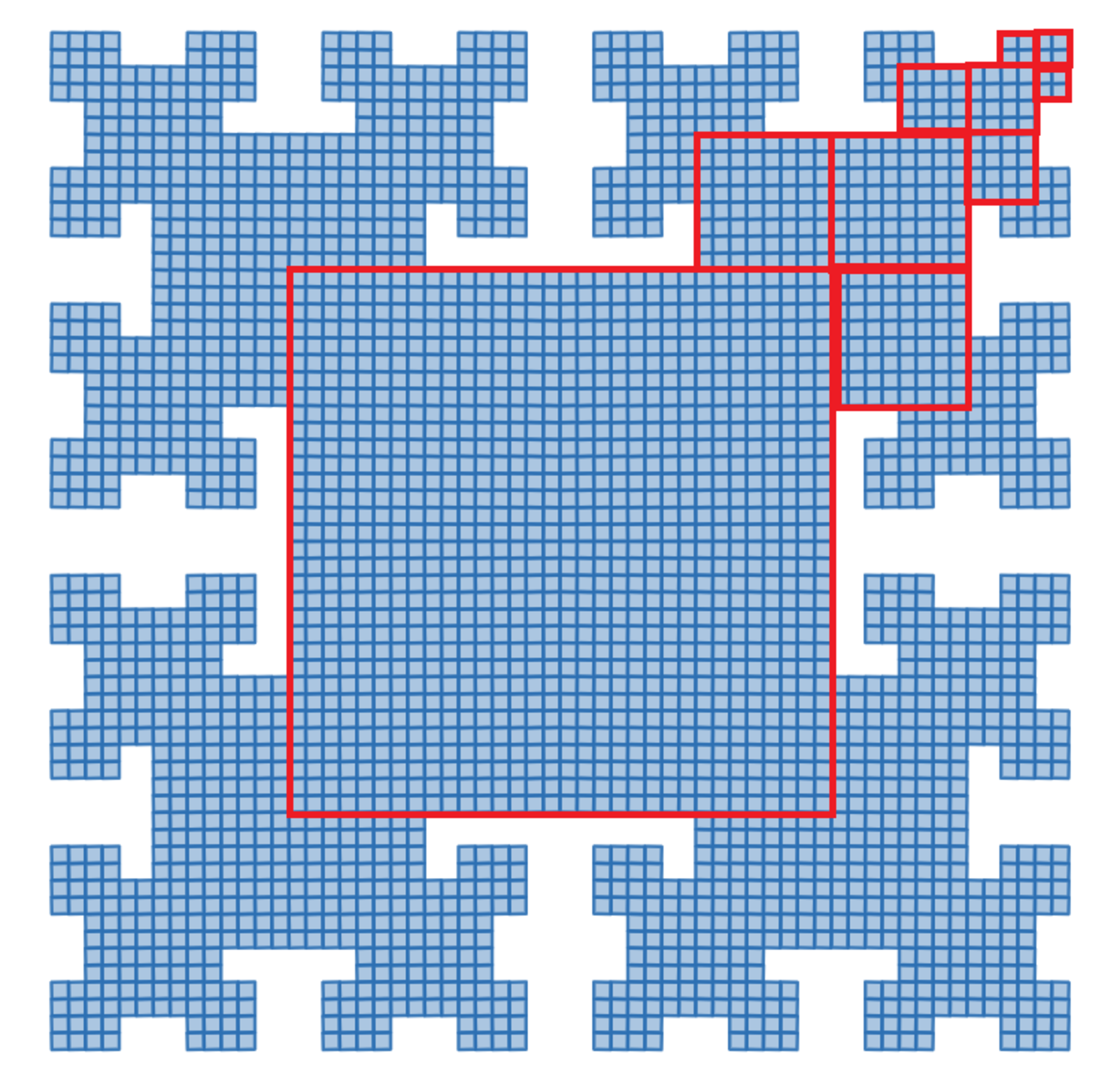正方形のカタマリに分割して数える
大きい正方形のカタマリから順に足し合わせていくと
$ 32^2+4\cdot3\cdot8^2+4\cdot9\cdot4^2+4\cdot27\cdot2^2=2800 $
これが一番簡単かもしれませんね。。
解法2 漸化式を作る
別の解法として、成長過程を観察して法則を見つけることで漸化式を作ることができます。
第１世代～第７世代
第 $1,2,4,8,\cdots$ 世代、つまり $2^n$ と表現できる世代で全体が正方形となり、その大きな正方形の4頂点を起点として過去の成長過程を繰り返していることがわかりますでしょうか。
新たに成長するときは、増える面積は$\dfrac{3}{4}\times4=3$ 倍に増えていますから、第 $n$ 世代の面積を $S(n)$ とすると次のような漸化式を作ることができます。
$s$ を $1\le 2^s \le n$ を満たす最大の整数とし、$t=n-2^s$ とするとき、次が成り立つ。
$ S(n)=S(2^s+t)=4^{s+1}+3S(t) $
ただし $S(0)=0$ とします。
この漸化式を繰り返し使うことで答えが得られます。
$ S(30)=S(2^4+14)=4^5+3S(14) $
$ S(14)=S(2^3+6)=4^{4}+3S(6) $
$ S(6)=S(2^2+2)=4^{3}+3S(2) $
$ S(2)=S(2^1+0)=4^{2} $
$ \begin{align} \therefore S(30)&=4^5+3 \cdot 4^4+3^2 \cdot 4^{3}+3^3\cdot 4^2\\ &=2800 \end{align} $
解法3 二進法を使う
さて、解法２に出てきた漸化式の形が $2$ 進法ととても相性がよさそうな形をしていますね?ですよね?
そのことを確認するために、$n$ を２進数で表したものと、漸化式から得られる式を並べてみましょう。
| $n$ | $2$進法 | 式 | S(n) |
|---|---|---|---|
| $1$ | $1$ | $4^1$ | $4$ |
| $2$ | $10$ | $4^2$ | $16$ |
| $3$ | $11$ | $4^2+3^1\cdot4^1$ | $28$ |
| $4$ | $100$ | $4^3$ | $64$ |
| $5$ | $101$ | $4^3+3^1\cdot4^1$ | $76$ |
| $6$ | $110$ | $4^3+3^1\cdot4^2$ | $112$ |
| $7$ | $111$ | $4^3+3^1\cdot4^2+3^2\cdot4^1$ | $148$ |
| $8$ | $1000$ | $4^4$ | $256$ |
| $9$ | $1001$ | $4^4+3^1\cdot4^1$ | $268$ |
この表から、次のルールで数列$a$、数列$b$を作り、それをもとに「式」を作ればいいことがわかります。
| $n$ | $2$進法 | 数列$a$ | 数列$b$ | 式 | $S(n)$ |
|---|---|---|---|---|---|
| $1$ | $1$ | $4^1$ | $1$ | $4^1$ | $4$ |
| $2$ | $10$ | $4^2$ | $1$ | $4^2$ | $16$ |
| $3$ | $11$ | $4^2,4^1$ | $1,3$ | $4^2+3^1\cdot4^1$ | $28$ |
| $4$ | $100$ | $4^3$ | $1$ | $4^3$ | $64$ |
| $5$ | $101$ | $4^3,4^1$ | $1,3$ | $4^3+3^1\cdot4^1$ | $76$ |
| $6$ | $110$ | $4^3,4^2$ | $1,3$ | $4^3+3^1\cdot4^2$ | $112$ |
| $7$ | $111$ | $4^3,4^2,4^1$ | $1,3,3^2$ | $4^3+3^1\cdot4^2+3^2\cdot4^1$ | $148$ |
| $8$ | $1000$ | $4^4$ | $1$ | $4^4$ | $256$ |
| $9$ | $1001$ | $4^4,4^1$ | $1,3$ | $4^4+3^1\cdot4^1$ | $268$ |
もう少し詳しく説明しましょう。
$a_{n,k}$ を「$n$ を $2$ 進法で表したときの下から $k+1$ 桁目の数」$(0\le k \le c_n)$
$b_{n,k}$ を「$n$ を $2$ 進法で表したときの下から $k+1$ 桁目以上の桁にある"$1$"の数」$(0\le k \le c_n)$
$c_n$ を 「($n$ を $2$ 進法で表したときの桁数) $- 1$」
とすると、$S(n)$ は次のようにあらわすことができることがわかります。
${\displaystyle S(n)=\sum_{i=0}^{c_n} 4^{i+1}\cdot a_{n,i}\cdot3^{b_{n,i}-1} }$
一般項を求める
さらに、$a_{n,k}$ , $b_{n,k}$ , $c_n$ は次のように表すことができますから
$a_{n,k}=\left\lfloor\dfrac{n}{2^k}-2\cdot \left\lfloor\dfrac{n}{2^{k+1}} \right\rfloor\right\rfloor$
${\displaystyle b_{n,k}= \sum_{j=0}^{c_n-k}a_{n,c_n-j}}$
$c_n=\left\lfloor \log_2 n \right\rfloor$
代入して整理すると一般項を次のように表すことができます。
${\displaystyle S(n)\ =\frac{4}{3}\sum_{i=0}^{\left\lfloor\log_2 n\right\rfloor} 4^i\cdot 3^{\left(\sum_{j=0}^{\left\lfloor\log_2 n\right\rfloor-i} \left\lfloor \frac{n}{2^{\left\lfloor\log_2 n\right\rfloor-j}} -2\left\lfloor\frac{n}{2^{\left\lfloor\log_2 n\right\rfloor-j+1}}\right\rfloor \right\rfloor \right)} \cdot \left\lfloor \frac{n}{2^{i}} -2\left\lfloor\frac{n}{2^{i+1}}\right\rfloor \right\rfloor }$
なかなかいかつい式になってしまいました。
解法4 階差数列を考える
階差数列を $d(n)$ とします。 $2$ 進法の表現と $d(n)/4$ を並べてみるとつぎのようになります。
| $n$ | $2$ 進法 | $d(n)/4$ |
|---|---|---|
| $1$ | $1$ | $3$ |
| $2$ | $10$ | $3$ |
| $3$ | $11$ | $3^2$ |
| $4$ | $100$ | $3$ |
| $5$ | $101$ | $3^2$ |
| $6$ | $110$ | $3^2$ |
| $7$ | $111$ | $3^3$ |
| $8$ | $1000$ | $3$ |
| $9$ | $1001$ | $3^2$ |
「$n$ を $2$ 進法で表したときの "$1$" の数」が、$3$ の指数になっていることが分かりますね。
つまり、$d(n)/4=3^{b_{n,0}}$ ということです。階差数列を足せば $S(n)$ を復元できますので
${\displaystyle S(n) =\sum_{i=0}^{n-1} 3d(i) =4\sum_{i=0}^{n-1} 3^{b_{i,0}} }$
この式に先ほどの式を代入することで次のような一般項が得られます。
${\displaystyle \begin{align} S(n)&= 4\sum_{i=0}^{n-1} 3^{b_{i,0}}\\ &=4\sum_{i=0}^{n-1} 3^{\sum_{j=0}^{c_i}a_{i,c_i-j}}\\ &=4\sum_{i=0}^{n-1} 3^{\sum_{j=0}^{c_i} \left\lfloor\dfrac{i}{2^{c_i-j}}-2\cdot \left\lfloor\dfrac{i}{2^{c_i-j+1}} \right\rfloor\right\rfloor}\\ \end{align} }$
解法5 第$32$世代 から考える
これは私の問題に対し、Oknow(@OknowC)さんが解いてくれたときの解法です。
${\displaystyle \begin{align} S(30) &=S(32)-d(31)-d(30)\\ &=4^6-4\cdot3^5-4\cdot3^4\\ &=4096-972-324\\ &=2800 \end{align} }$
これは計算が楽ですね!
おわりに
なんとなく作ってみた問題でしたが、再帰的な構造がなかなか楽しいですね。
ちょっと競技プログラミングぽい問題になった気がします。
競技プログラミングなら、$S(N)$ を $1\le N \le10^9$ の制約で求めよ、みたいになって、解法$4$だと TLE になって、解法$3$ で AC になりそうですね。
フォロワーさんの数もこの問題のようにじわじわ増えてきました。
みなさんのフォローありがとうございます。
今後ともよろしくお願いします!
最後に、この問題のために作ったDesmosファイルを置いておきますので遊んでみてくださいね。
この記事を高評価した人
この記事に送られたバッジ
投稿者
