九点円の中心がオイラー線上にあることの初等的な証明
目次
- はじめに
- オイラー線とは？
- 証明
- 終わりに
1.はじめに
こんにちは.今回は,九点円の中心がオイラー線上にあることを初等的に示すことができたので紹介します.僕調べですが,なかなか証明をくわしく紹介している記事がなかったのでここで紹介します.
※今回は九点円の存在や基本的な性質は認めているものとします.
2.オイラー線とは？
正三角形でない任意の三角形に対して外心,重心,垂心はこの順で一直線に並びその距離の比は$1:2$である.この線のことをオイラー線と呼ぶ.
直線$CO$と円との交点を$P$とする.この時,$CP$は円の直径である.また,$BC$の中点を$M$とすると,中点連結定理より,$OM//PB$であり,$2|OM|=|PB|$である.$ AD\perp BC, PB\perp BC $であるから,$AD // PB$である.また,垂心の性質と円周角の定理より,$ BE\perp AC, PA\perp AC $であるから,$BE//PA$である.よって,四角形$PBHA$は平行四辺形である.よって,$|AH|=|PB|=2|OM|$
図2において,三角形$AGH$と三角形$MGO$は$ \angle MGO = \angle AGH$,$\angle GAH = \angle GMO (\because AD//OM)$であるから,相似である.さらに,$|AH|=2|OM|$より,その相似比は$2:1$である.また,$G$は$AM$を$2:1$に内分する点で$M$が中点であるから$G$は重心である.これより,三点$O,G,H$は一直線条に並び,$|OG|:|GH|=1:2$である.
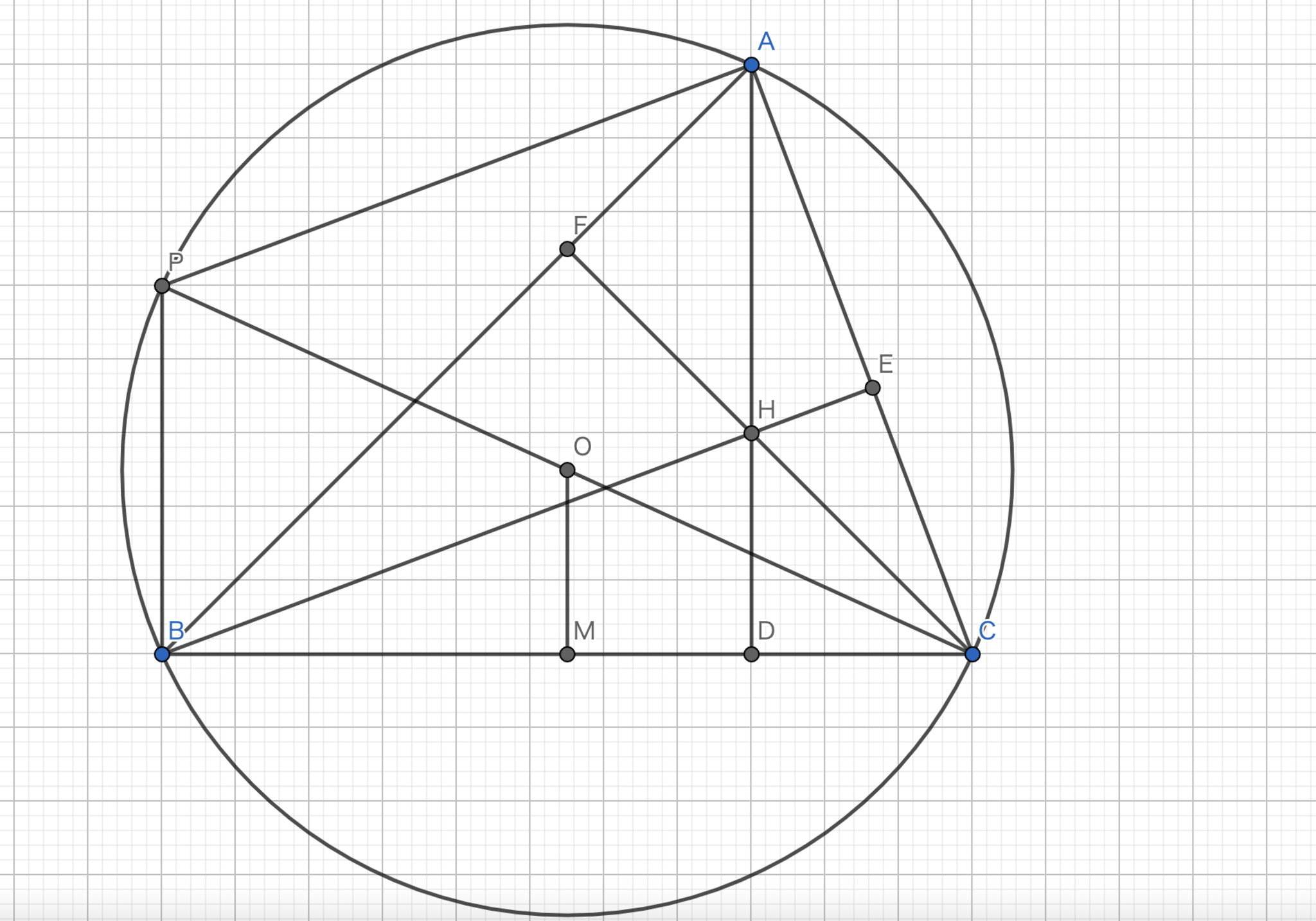オイラー線の復習
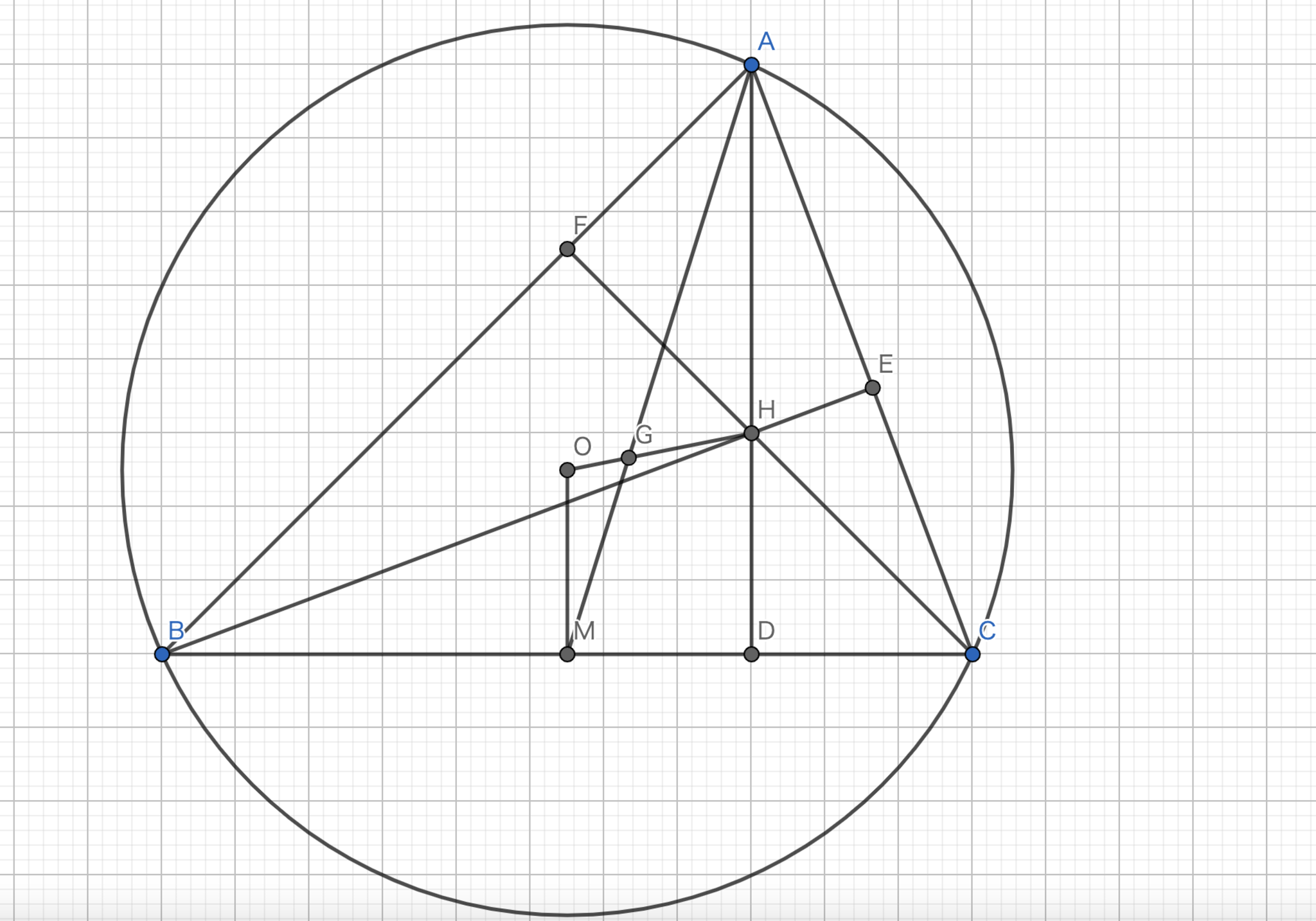オイラー線の復習(2)
今回はこのオイラー線の上に九点円が存在することを示してみます.
3.証明
九点円の中心は外心と垂心の中点である.
中点三角形の垂心は元の三角形の外心である.
中点三角形の垂心は元の三角形の各辺の垂直二等分線の交点であって,それは外心である.
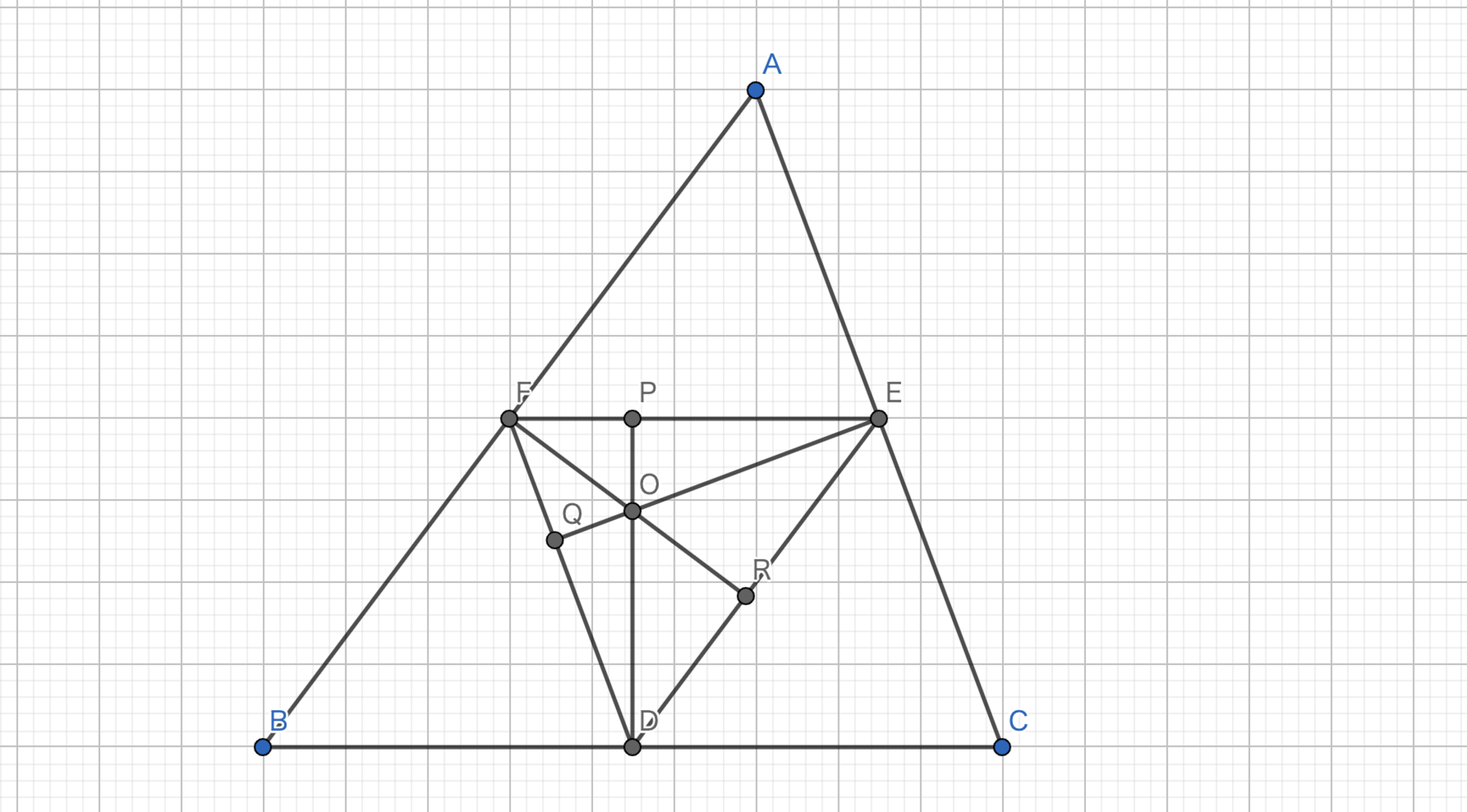中点三角形-垂心
三角形$PQR$は垂心$D$を中心として$0°$回転させて$\frac{1}{2}$の相似比で拡大させたものである.また,$PQR$の外接円は九点円である.三角形$M_{A}M_{B}M_{C}$は外心$O$を中心として$180°$回転させて$\frac{1}{2}$の相似比で拡大させたものである.また,三角形$M_{A}M_{B}M_{C}$の外接円は九点円である.補題2より,中点三角形の垂心は元の三角形の外心であるから$O_{1}$と$D$は共に垂心である.さらに,これらの二つの三角形は九点円を共有して180°回転した合同であるから$O_{1}$と$D$は$O_{2}$を中心とする対称な点である.よって,九点円の中心は外心と垂心の中心である.
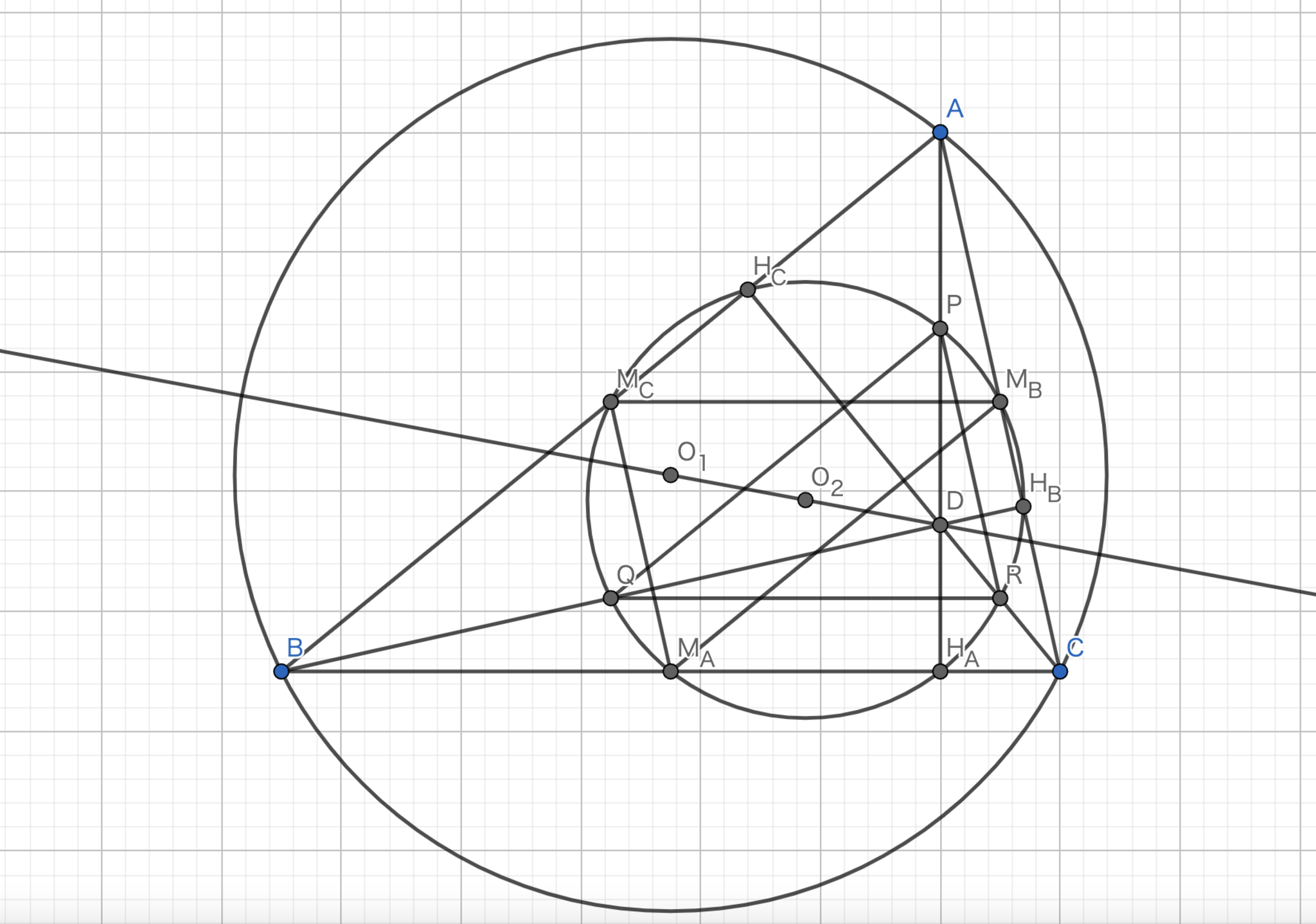九点円
4.終わりに
まとめとして,定理の形で表しましょう.
正三角形でない任意の三角形の外心,重心,九点円の中心,垂心はこの順で一直線に並び,その距離の比率は$2:1:3$である.
拙い記事でしたが,見ていただきありがとうございました!!
