多角形の"中心"から見る平面幾何(五心の基本性質まとめ)
はじめに
こんにちは.この記事では僕の幾何力向上を兼ねて五心の性質と五心関連の話を整理していきたいと思います.その性質上とても記事が長くなってしまっています.何かミス等ありましたらご指摘いただけると嬉しいです.出来るだけ色々な解法で解くとともに,なぜそのように考えるのか?等もメモしていきたいと思います.では,よろしくお願いします!
(ちなみに,4.利用例には軽く五心の性質を使う問題たちを載せておきました.おまけです.)
この記事をほぼ理解するための前提知識は,中学数学と数学Aのチェバの定理,メネラウスの定理までです.(終盤の難しめの定理に関しては一部複素を使って証明しています.)
<今回紹介するもの>
今回紹介するものは目次の通りです.前半の方はとても簡単で一つ一つが軽いです.後半はかなり重めの定理なども含まれています.また,五心が関わるものなら割と広く紹介していますので九点円なども含まれています.
本記事に修正、加筆を加えた 最新版 もぜひご覧ください。
五心の定義と存在
重心の存在
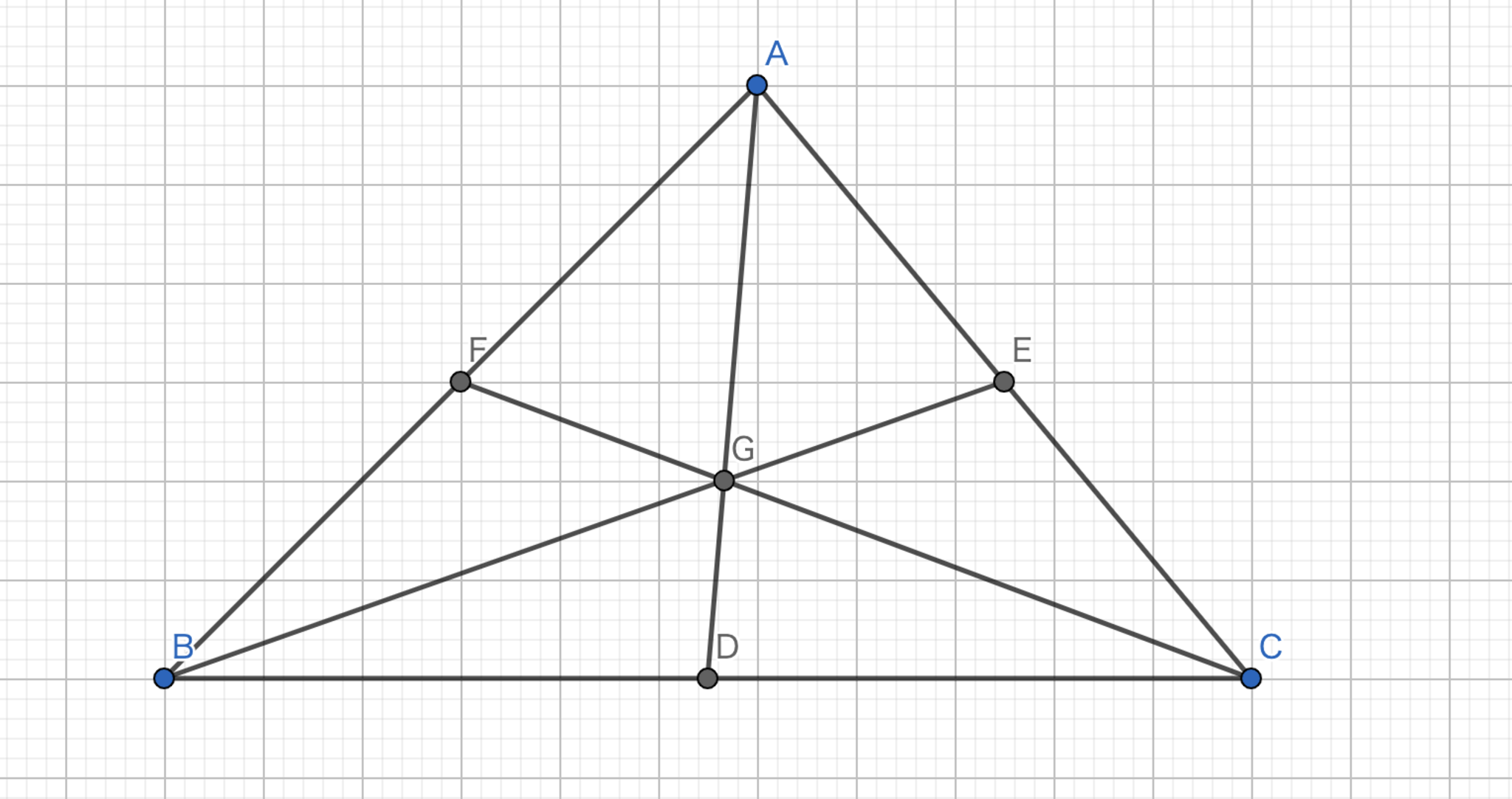
三角形の各頂点から対辺への中線の交点を重心という.
三角形の各頂点から対辺への中線は必ず一点で交わる.(重心は必ず存在する.)
三角形$ABC$の各辺の中点を$D,E,F$とすれば,チェバの定理の逆より$\frac{|AF|}{|FB|} \cdot \frac{|BD|}{|DC|} \cdot \frac{|CE|}{|EA|}= \frac{1}{1} \cdot \frac{1}{1} \cdot \frac{1}{1}=1$であるから一点で交わる.
 重心-1
重心-1
内心の存在
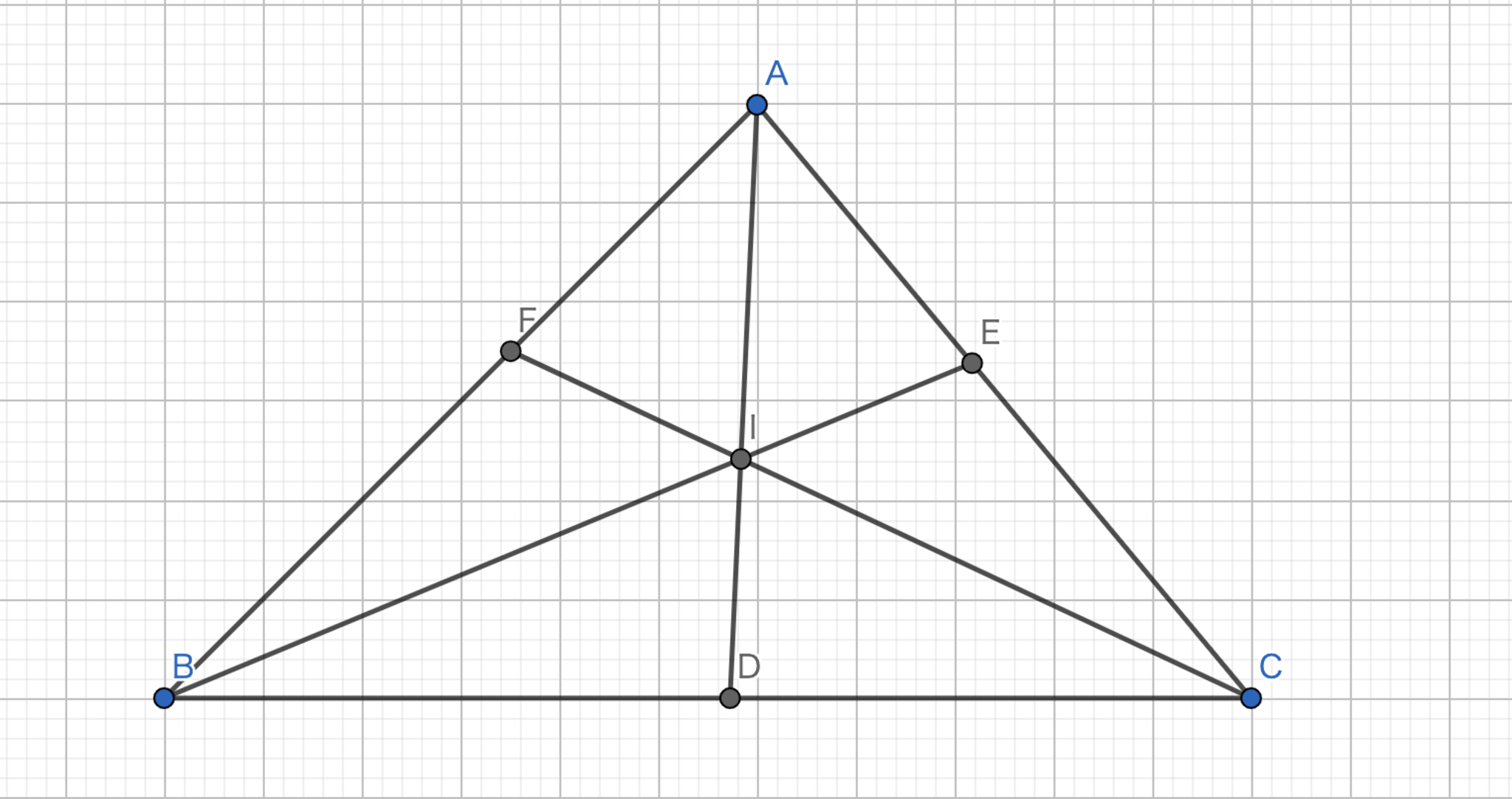
三角形の各頂点の角の二等分線の交点を内心という.
三角形の各頂点の角の二等分線は一点で交わる.(内心は必ず存在する.)
三角形$ABC$において,角$A$の二等分線と対辺の交点を$D$,角$B$の二等分線と対辺の交点を$E$,角$C$の二等分線と対辺の交点を$F$とすれば,チェバの定理の逆より,$\frac{|AF|}{|FB|} \cdot \frac{|BD|}{|DC|} \cdot \frac{|CE|}{|EA|}= \frac{|CA|}{|BC|} \cdot \frac{|AB|}{|CA|} \cdot \frac{|BC|}{|AB|}=1$であるから一点で交わる.
 内心-1
内心-1
方針:まず二つの角の二等分線の交点を考えその交点と残りの頂点を結ぶ線が角の二等分線であることを示す.
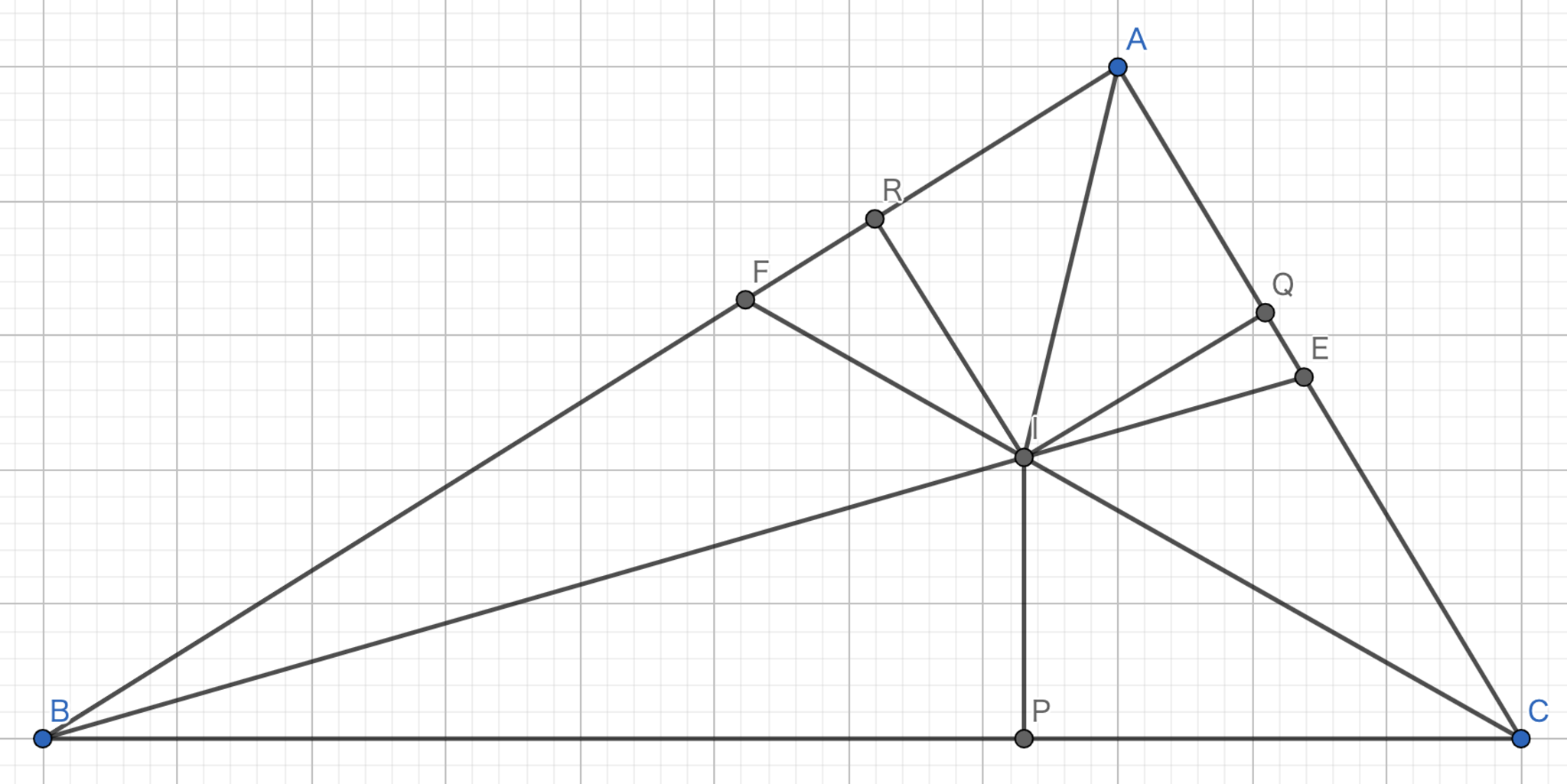
三角形$ABC$において,角$B$の二等分線と角$C$の二等分線の交点を$I$とする.$I$から各辺へ下ろした垂線の足をそれぞれ$P,Q,R$とする.(図を参照)
ここで,$ \angle RBI = \angle PBI $,$ \angle BPI= \angle BRI =90° $であり,$BI$が共通であるため$ \triangle RBI \equiv \triangle PBI $が成り立つ.よって,$|RI|=|PI|$である.同様に,$|QI|=|PI|$が得られる.このことから$|RI|=|QI|$である.
$\angle ARI=\angle ARI=90°$,$|RI|=|QI|$であって,$AI$が共通なので$\triangle ARI\equiv \triangle AQI $となる.よって,$\angle IAR=\angle IAQ$が従う.このことより,線分$AI$は角$A$の二等分線であることが示された.
 内心-02
内心-02
角の二等分線が$I$を通ることを示すのは難しいですが,$I$を通る線分が角の二等分線であることを示すのは簡単ですからね.チェバの定理は便利ですが,合同の考え方も大事なので両方使えるようにしておきましょう.難しい問題でよく使う考え方は後半の合同の方です.
外心の存在
三角形の各辺の垂直二等分線の交点を外心という.
三角形の各辺の垂直二等分線は一点で交わる.(外心は必ず存在する.)
方針:まず二つの辺の垂直二等分線の交点を考えその交点から残りの辺への垂線を下ろす.その点が中点であることを示す.
$AB$の垂直二等分線と$CA$の垂直二等分線の交点を$O$とする.$O$から$BC$へ下ろした垂線の足を$D$とする.また,$AB,CA$の中点を$F,E$とする.
ここで,$F$は$AB$の中点であるから,$|AF|=|FB|$である.また,$\angle AFO= \angle BFO = 90°$で$OF$が共通なので,$\triangle AFO\equiv \triangle BFO$である.同様に,$\triangle AEO\equiv \triangle CEO$である.このことから,$|OB|=|OC|$が従う.よって,三角形$OBC$は二等辺三角形である.二等辺三角形の頂角から下ろした垂線は底辺の中点と交わるので$D$は$BC$の中点である.よって,$OD$は垂直二等分線であるから題意は示された.
 外心-1
外心-1
垂心の存在
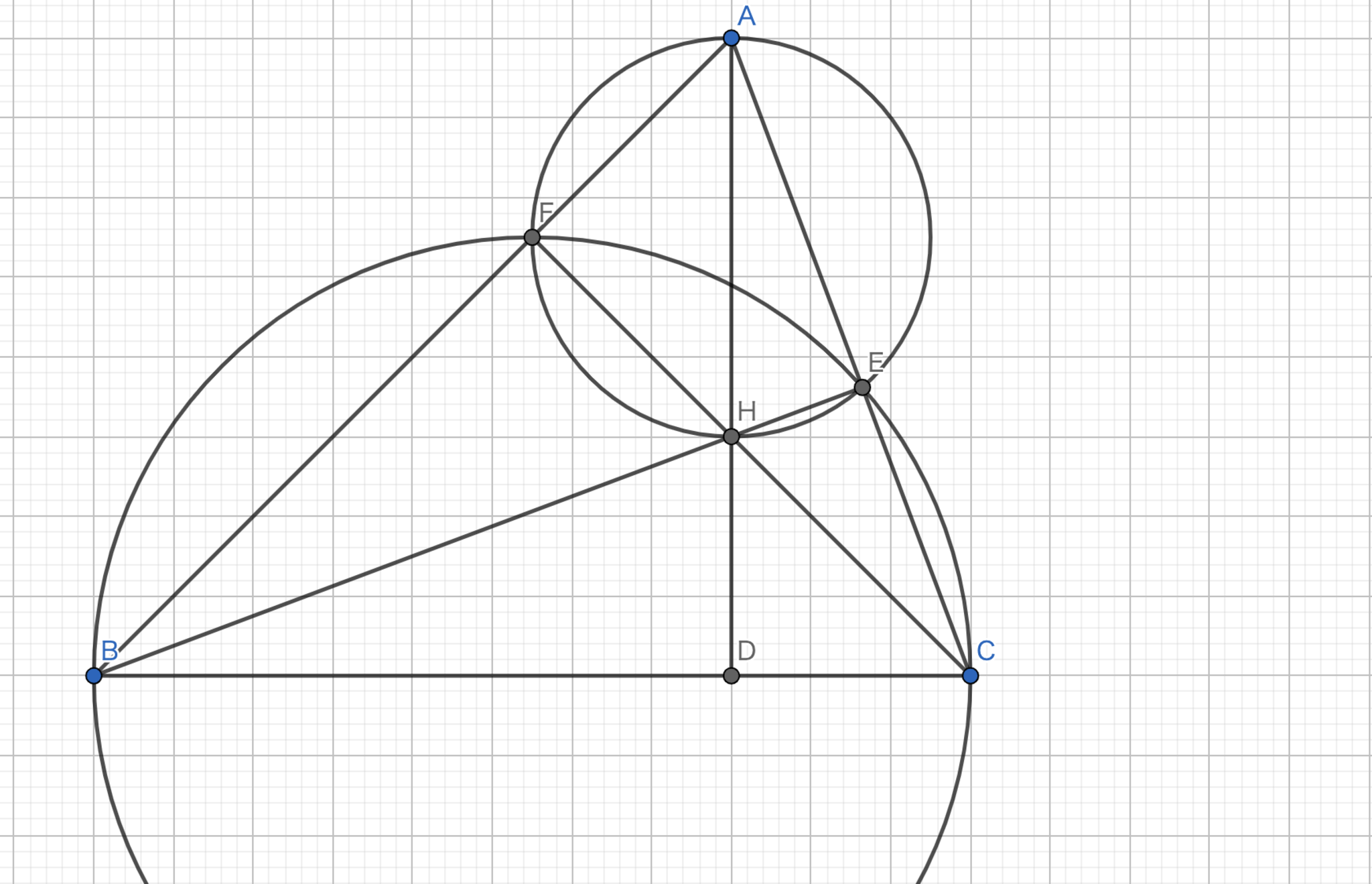
三角形の各頂点から対辺へ下ろした垂線の交点を垂心という.
三角形の各頂点から対辺へ下ろした垂線は一点で交わる.(垂心は必ず存在する.)
方針:共円の存在を利用して角度計算をして示す.
$B$から$CA$へと下ろした垂線の足を$E$とする.同様に$C$から$AB$へと下ろした垂線の足を$F$とする.$A$と$H$を通る直線と$BC$との交点を$D$とする.
$\angle AFH= \angle AEH = 90°$であるので,$AFHE$は共円である.このことから円周角の定理より,$\angle FAH = \angle FEH = \angle FCB$が従う.$\angle ADB= 180°-\angle BED - \angle ABD =180°- \angle FCB - \angle ABD = 180°-\angle FCB -(180°-90°-\angle BAD)=90°$よって,$AD$は垂線であるから題意は示された.
 垂心-1
垂心-1
方針:外心の存在を利用する.
各頂点を通り,対辺に並行な直線をそれぞれ引く.それらの交点を図のように$P,Q,R$とする.すると,中点連結定理より,$A$は$QR$の中点になる.同様に,$B,C$はそれぞれ$RP,PQ$の中点になる.また,$QR // BC$より,$ AD \perp QR$であるから$AD$は$QR$の垂直二等分線である.同様に,$BE,CF$はそれぞれ$RP,PQ$の垂直二等分線である.このことから,$H$は三角形$PQR$の外心である.定理3(外心の存在)より,題意は示された.
 垂心-2
垂心-2
傍心の存在
三角形の頂点一つの角の二等分線と二つの外角の二等分線の交点を傍心という.
三角形の頂点一つの角の二等分線と二つの外角の二等分線の交点は一点で交わる.(傍心は必ず存在する.)
一つの三角形に対して,傍心は3つ存在します.
方針:外角の二等分線の交点と$A$を結んだ線分が角$A$の内角の二等分線であることを示す.(傍心は内心とほぼ一緒です.)
$I_{A}$から$AB,BC,AC$へと垂線を下ろす.その足をそれぞれ$D,E,F$とする. $\angle DBI_{A} =\angle EBI_{A}$であり,$\angle BDI_{A}=\angle BEI_{A} =90°$で$BI_{A}$が共通であるから,$\triangle DBI_{A}\equiv \triangle EBI_{A}$である.同様に,$\triangle FCI_{A}\equiv \triangle ECI_{A}$である.よって,$|DI_{A}|=|EI_{A}|=|FI_{A}|$が従う.$\angle ADI_{A}=\angle AFI_{A} = 90°$であり,$|DI_{A}|=|FI_{A}|$で$AI_{A}$が共通であるから$\triangle ADI_{A}\equiv \triangle AFI_{A}$である.従って,$AI_{A}$は角$A$の内角の二等分線である.題意は示された.
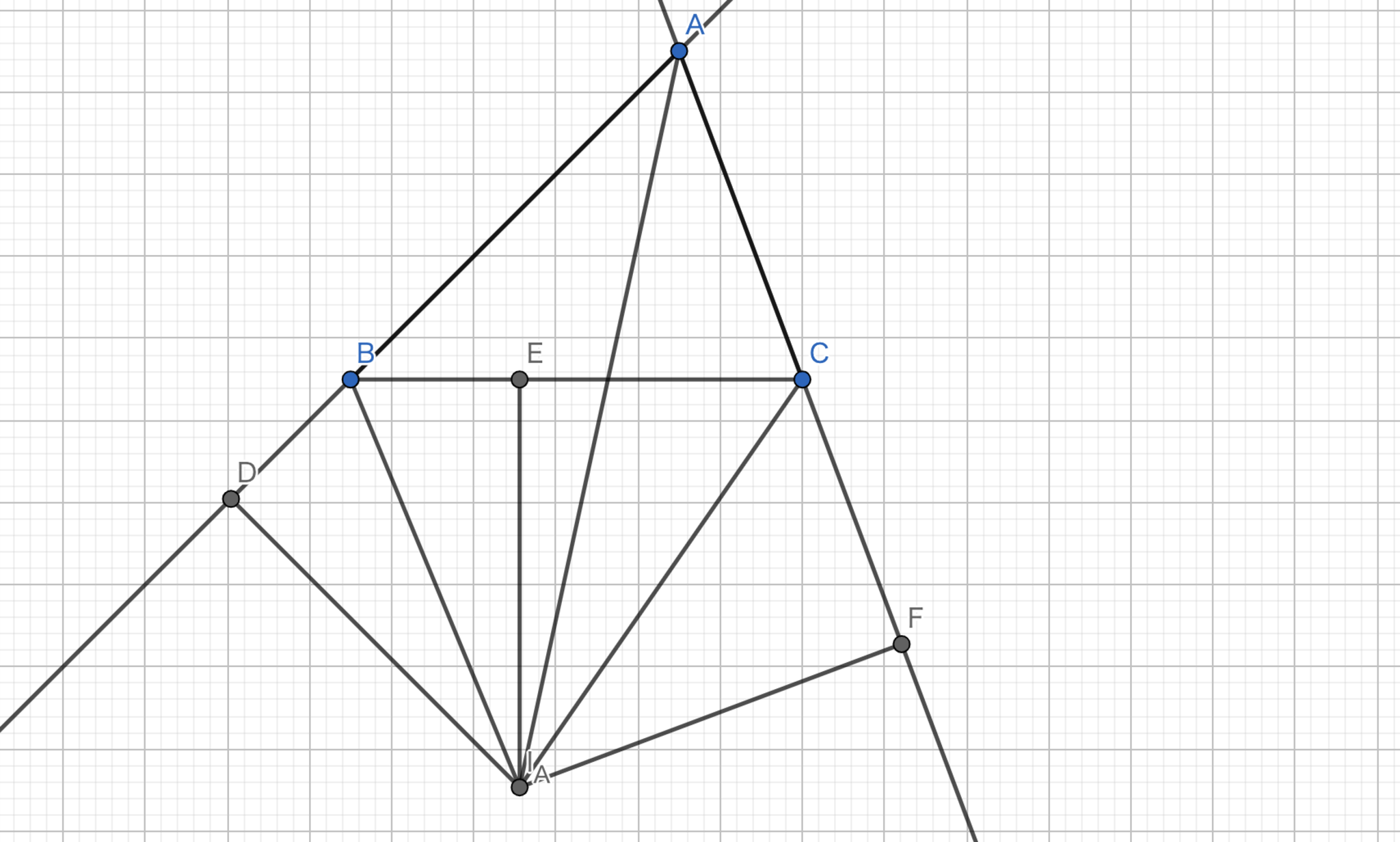 傍心-1
傍心-1
五心の性質
内接円の半径
三辺の長さを$a,b,c$とする三角形の内接円の半径$r$は
$$r=\frac{2S}{a+b+c}=\frac{1}{2}\sqrt{\frac{\left(-a+b+c\right)\left(a-b+c\right)\left(a+b-c\right)}{a+b+c}}$$
三角形$ABC$の面積を$S$とすると,$S=\frac{r\left(a+b+c\right)}{2}$である.これを$r$について解くと$r=\frac{2S}{a+b+c}$が得られる.また,$S$をヘロンの公式を用いて$a,b,c$で表すと,
$$
\begin{align*}
r & =\frac{2\sqrt{\left(\frac{a+b+c}{2}\right)\left(\frac{-a+b+c}{2}\right)\left(\frac{a-b+c}{2}\right)\left(\frac{a+b-c}{2}\right)}}{a+b+c} \\
& = \sqrt{\frac{4\left(a+b+c\right)\left(-a+b+c\right)\left(a-b+c\right)\left(a+b-c\right)}{16\left(a+b+c\right)^{2}}} \\
& = \frac{1}{2}\sqrt{\frac{\left(-a+b+c\right)\left(a-b+c\right)\left(a+b-c\right)}{a+b+c}}
\end{align*}
$$
となって,最右辺が得られる.
 内接円-1
内接円-1
外接円の半径
三辺の長さを$a,b,c$とする三角形の外接円の半径$R$は
$$
R=\frac{a}{2\sin A}=\frac{abc}{4S}=\frac{abc}{\sqrt{\left(a+b+c\right)\left(-a+b+c\right)\left(a-b+c\right)\left(a+b-c\right)}}
$$
図のように$A'$をとる.
円周角の定理より,$\angle BAC=\angle BA'C$である.また,$2Rsin\angle BA'C = 2Rsin\angle BAC= a$であるからこれを$R$について解くことで$R=\frac{a}{2\sin A}$が得られる.同様に,$R=\frac{a}{2\sin A}=\frac{b}{2\sin B}=\frac{c}{2\sin C}$が得られる.
$S=\frac{1}{2}bc\sin A $であるので,$\sin A=\frac{2S}{bc}$が得られる.これを$R=\frac{a}{2\sin A}$に代入すると,$\frac{a}{2\frac{2S}{bc}}=\frac{abc}{4S}$が得られ,題意は示された.
最右辺に関しては内接円の半径と同じように,$S$をヘロンの公式を用いて$a,b,c$のみで表すことで得られる.
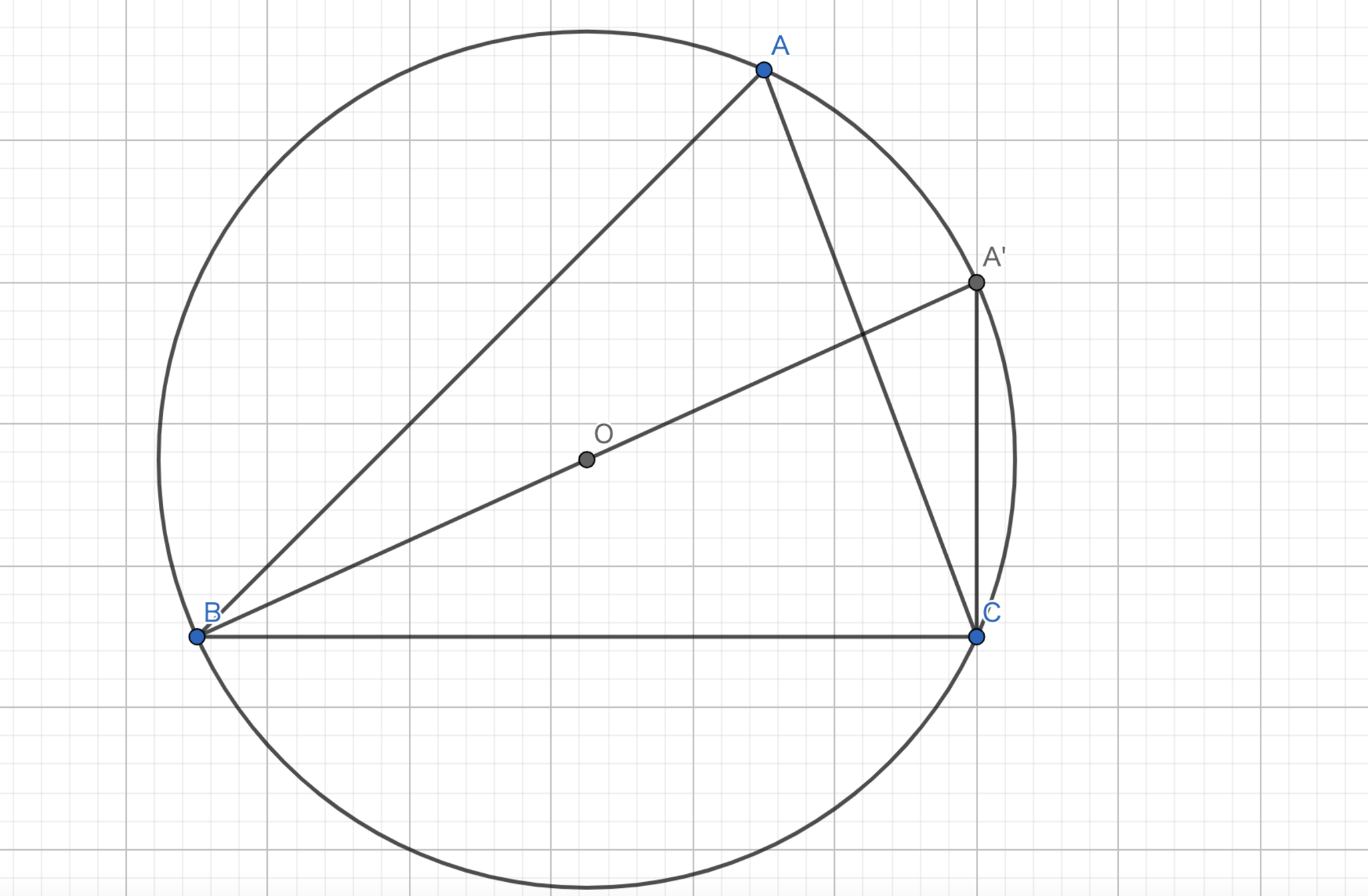 正弦定理-1
正弦定理-1
傍接円の半径
三辺の長さを$a,b,c$とする三角形の$A$に関する傍接円の半径$r_{A}$は
$$
r_{A}=\frac{2S}{-a+b+c}=\frac{1}{2}\sqrt{\frac{\left(a+b+c\right)\left(a-b+c\right)\left(a+b-c\right)}{\left(-a+b+c\right)}}
$$
方針:内接円の半径と同様に面積についての式を立てる.
$|AB|=c,|BC|=a,|CA|=b,|I_{A}E|=r_{A}$とすると,面積$S$について,以下の式が成り立つ.
$S= \triangle ABI_{A}+ \triangle ACI_{A}- \triangle BCI_{A}=\frac{cr_{A}}{2}+\frac{br_{A}}{2}-\frac{ar_{A}}{2}=\frac{1}{2}r_{A}\left(-a+b+c\right)$が得られる.これを$r_{A}$について解くと$r_{A}=\frac{2S}{-a+b+c}$が得られる.
最右辺に関しては内接円と同じように,Sをヘロンの公式を用いて$a,b,c$のみで表すことで得られる.
 傍接円-1
傍接円-1
リュイリエの定理
三角形$ABC$において,内接円の半径を$r$,傍接円の半径を$r_{A},r_{B},r_{C}$とすると,以下の式が成り立つ.
$$\frac{1}{r}=\frac{1}{r_{A}}+\frac{1}{r_{B}}+\frac{1}{r_{C}}$$
定理6より$\frac{1}{r}=\frac{a+b+c}{2S}$,定理8より$\frac{1}{r_{A}}=\frac{-a+b+c}{2S},\frac{1}{r_{B}}=\frac{a-b+c}{2S},\frac{1}{r_{C}}=\frac{a+b-c}{2S}$である.
$$
\begin{align*}
\frac{1}{r_{A}}+\frac{1}{r_{B}}+\frac{1}{r_{C}} & = \frac{\left(-a+b+c\right)+\left(a-b+c\right)+\left(a+b-c\right)}{2S}\\
& =\frac{a+b+c}{2S} \\
& = \frac{1}{r}
\end{align*}
$$
よって,題意は示された.
内接円,傍接円の半径と面積の関係
三角形$ABC$において,内接円の半径を$r$,傍接円の半径を$r_{A},r_{B},r_{C}$とすると,以下の式が成り立つ.
$$
S=\sqrt{rr_{A}r_{B}r_{c}}
$$
定理6より$r=\frac{2S}{a+b+c}$,定理8より$r_{A}=\frac{2S}{-a+b+c},\ r_{B}=\frac{2S}{a-b+c},\ r_{C}=\frac{2S}{a+b-c}$である.
$$ \begin{align*} \sqrt{rr_{A}r_{B}r_{c}} & = \sqrt{\frac{2S}{a+b+c}\cdot\frac{2S}{-a+b+c}\cdot\frac{2S}{a-b+c}\cdot\frac{2S}{a+b-c}} \\ & = \sqrt{\frac{16S^{4}}{16S^{2}}} \\ & = S \end{align*} $$
九点円の存在
三角形の三辺の中点,三頂点から対辺に下ろした垂線の足,垂心と各頂点の中点を通る円を九点円(フォイエルバッハ円)という.
三角形の三辺の中点,三頂点から対辺に下ろした垂線の足,垂心と各頂点の中点は同一円周上に存在する.(九点円は必ず存在する.)
方針:中点が複数存在することから中点連結定理を考える.
三角形$ABC$に注目すると,中点連結定理より,$M_{C}M_{B}//BC$, $|M_{C}M_{B}|=\frac{1}{2}\left|BC\right|$がわかる.また,三角形$DBC$に注目すると,中点連結定理より,$QR//BC$, $|QR|=\frac{1}{2}\left|BC\right|$がわかる.このことから,四角形$M_{C}QRM_{B}$は長方形である.故に四点$M_{C}QRM_{B}$は$M_{C}R,M_{B}Q$を直径とする共円である.また,円周角の定理の逆より$H_{C},H_{B}$も共円である.さらに,この円は三角形$H_{B}M_{B}Q$の外接円である.
四角形$M_{C}QRM_{B}$と同様に,四角形$M_{B}PQM_{A}$は長方形である.さらに,円周角の定理の逆より$H_{A},H_{B}$も共円である.この円は三角形$H_{B}M_{B}Q$の外接円であるから,先ほどの円と等しい円である.よって,九点は共円である.
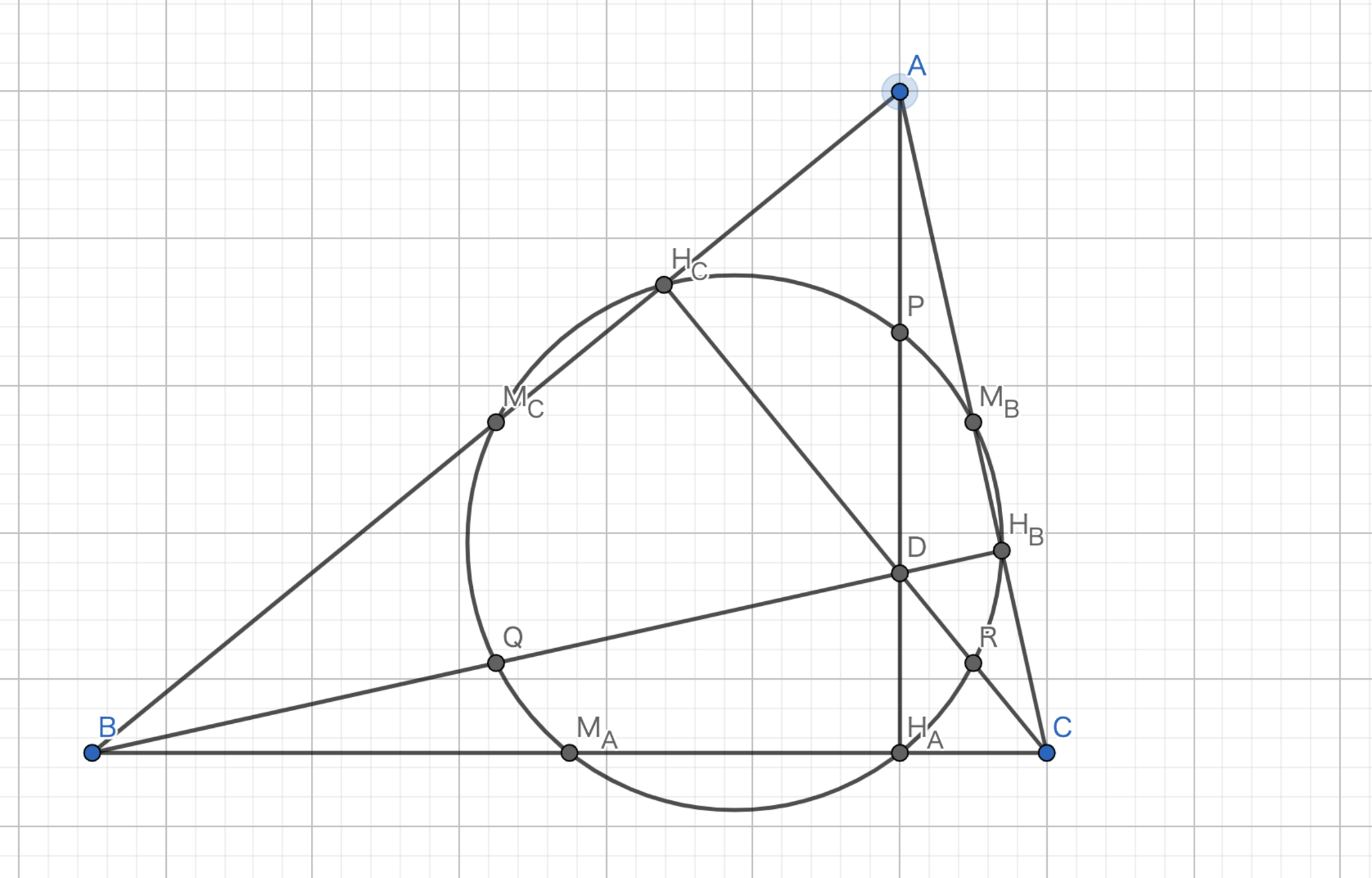 九点円-1
九点円-1
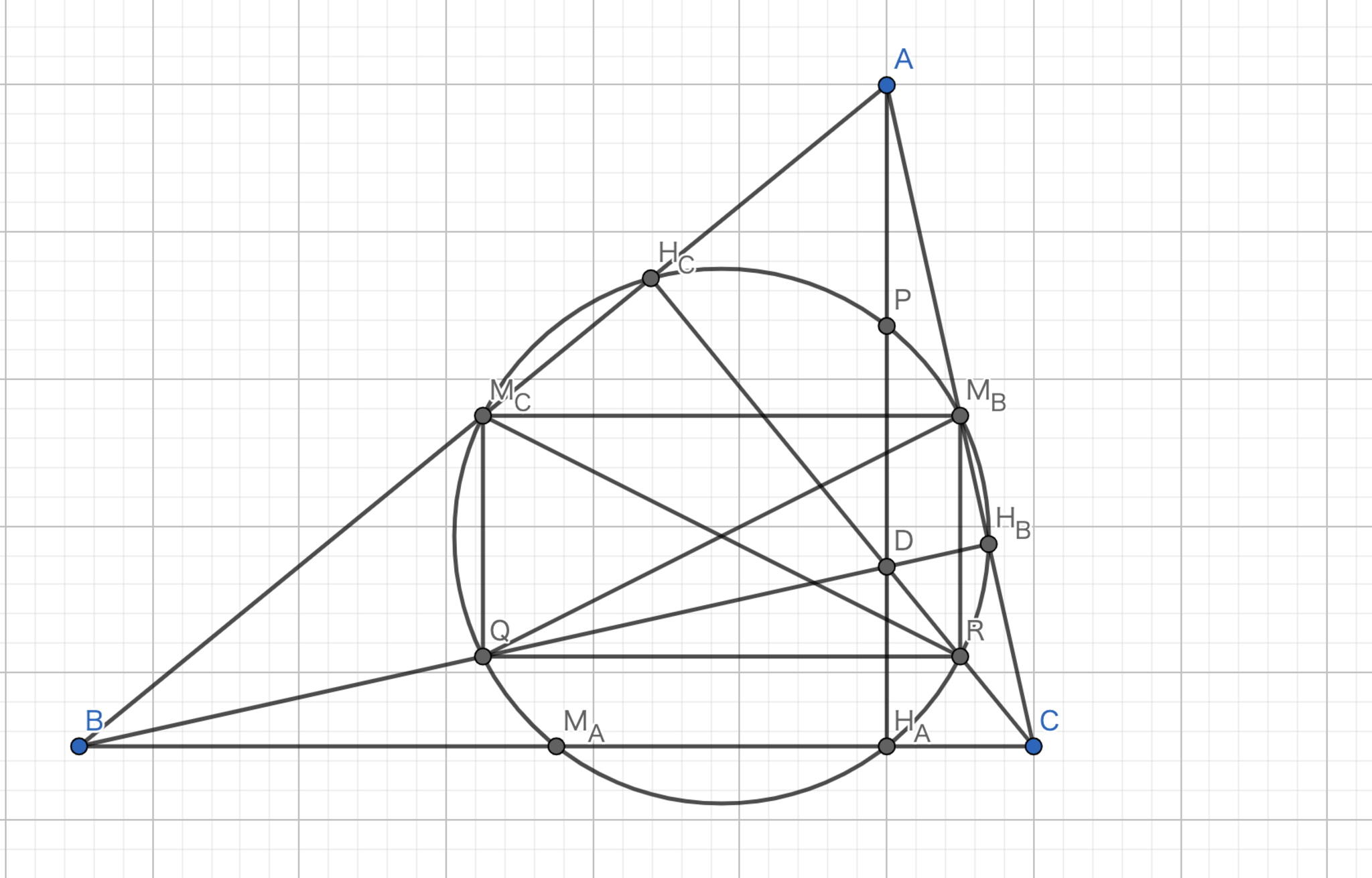 九点円-2
九点円-2
九点円の半径
九点円の半径は外接円の半径の半分である.
定理12を示す前に補題を示しておきます.
三角形の各辺の中点を結んでできた三角形(中点三角形)は元の三角形と相似であり,その相似比は$1:2$である.
中点連結定理より,$|DE|:|BA|=|EF|:|CB|=|FD|:|CA|=1:2$である.よって,三角形$DEF$は三角形$ABC$と相似であり,その相似比は$1:2$である.
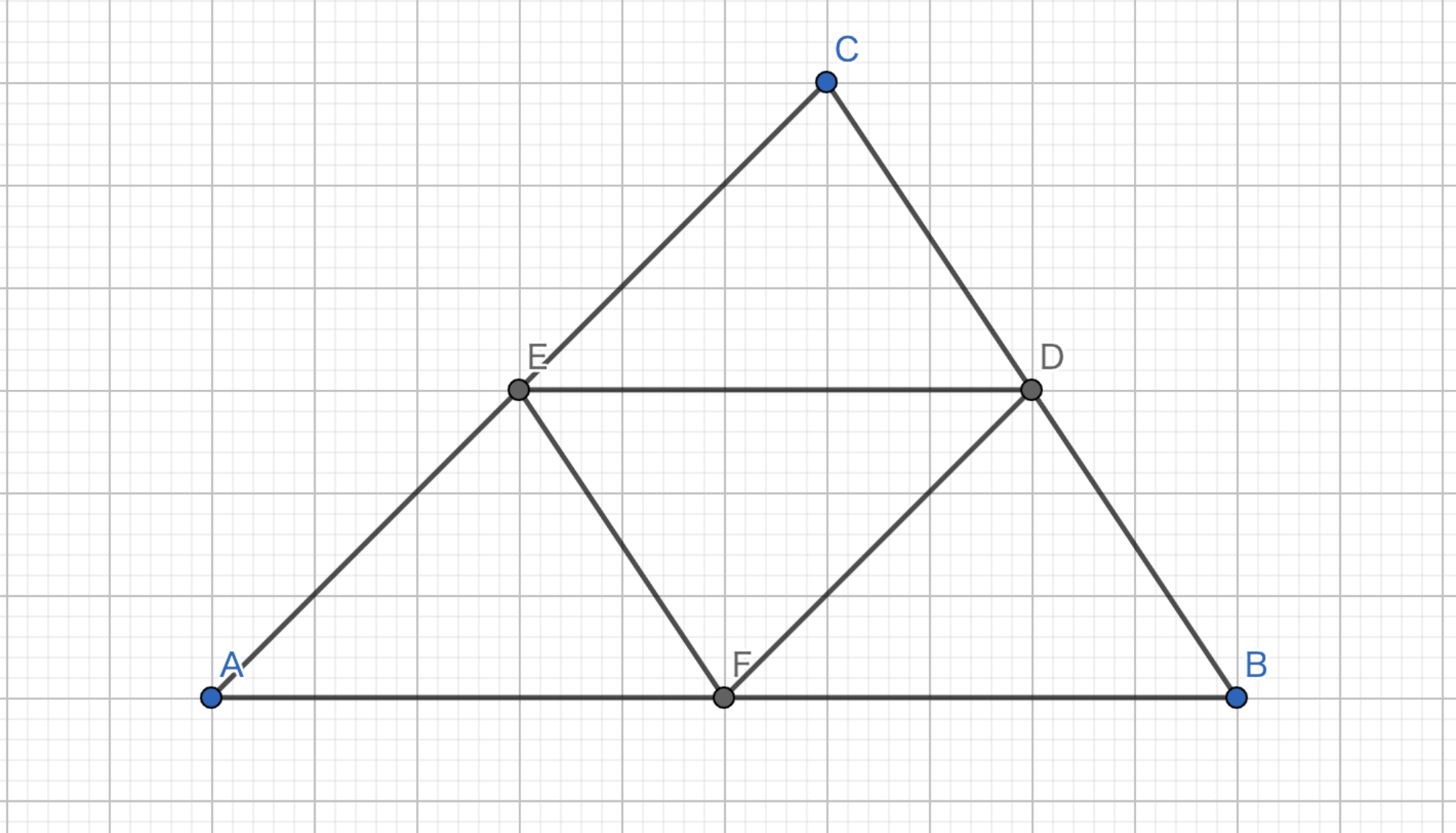 中点三角形-1
中点三角形-1
補題13より,三角形$M_{A}M_{B}M_{C}$は三角形$ABC$と相似でありその比は$1:2$であるから外接円の半径も$1:2$である.九点円は三角形$M_{A}M_{B}M_{C}$の外接円であるから題意は示された.
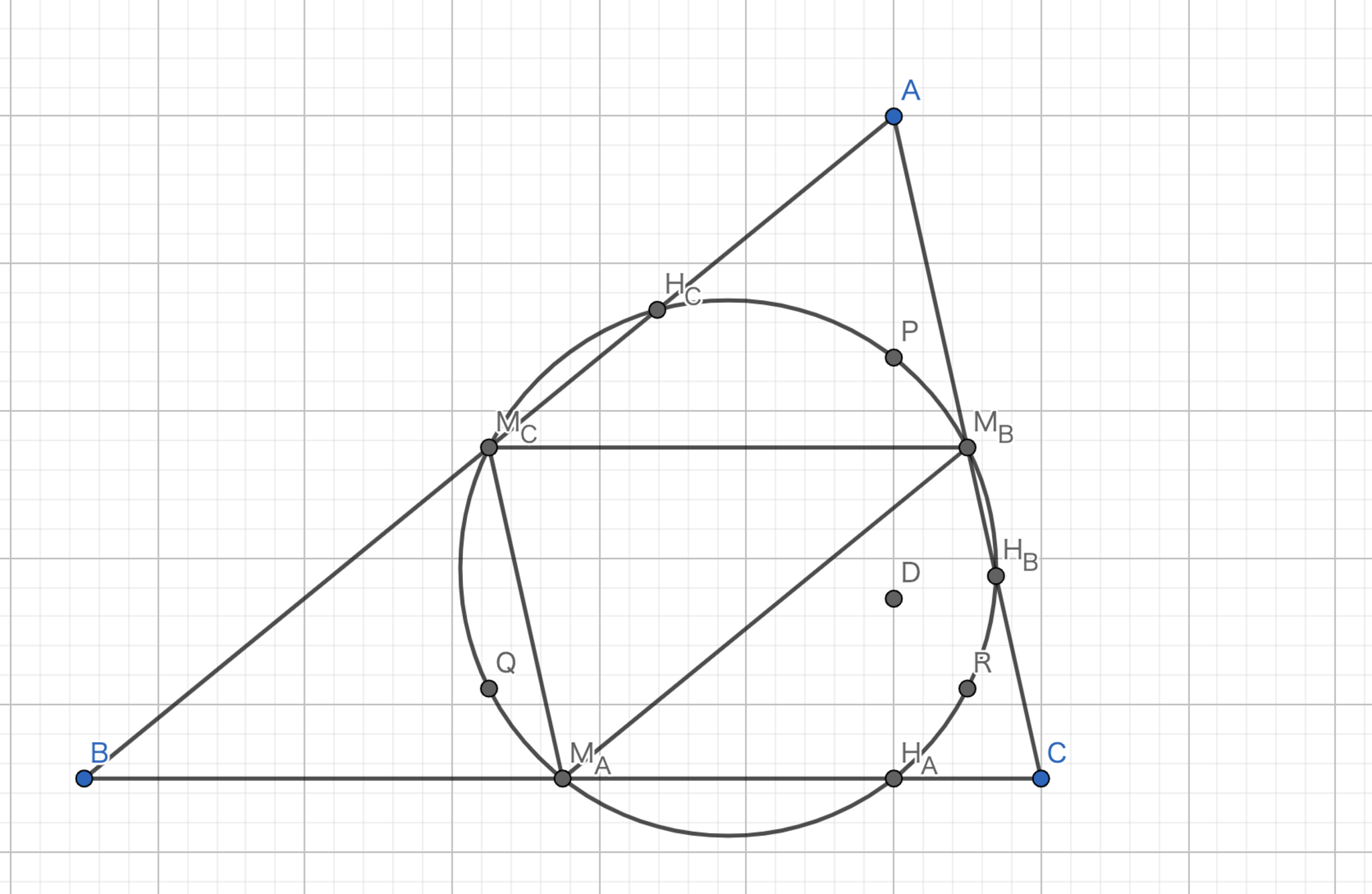 九点円-3
九点円-3
九点円の中心と外心と垂心
九点円の中心は外心と垂心の中点である.
三角形$PQR$は垂心$D$を中心として$0°$回転させて$\frac{1}{2}$の相似比で拡大させたものである.また,$PQR$の外接円は九点円である.三角形$M_{A}M_{B}M_{C}$は外心$O$を中心として$180°$回転させて$\frac{1}{2}$の相似比で拡大させたものである.また,三角形$M_{A}M_{B}M_{C}$の外接円は九点円である.後述する定理16より,中点三角形の垂心は元の三角形の外心であるから$O_{1}$と$D$は共に垂心である.さらに,これらの二つの三角形は九点円を共有して180°回転した合同であるから$O_{1}$と$D$は$O_{2}$を中心とする対称な点である.よって,九点円の中心は外心と垂心の中心である.
 九点円とオイラー線-1
九点円とオイラー線-1
中点三角形の重心
中点三角形の重心は元の三角形の重心と等しい.
中点連結定理より,$H$は$EF$の中点である.また,$AD$は$H$を通る.同様に,$BE$は$I$を,$CF$は$J$を通る.よって,$G$は元の三角形の重心である.
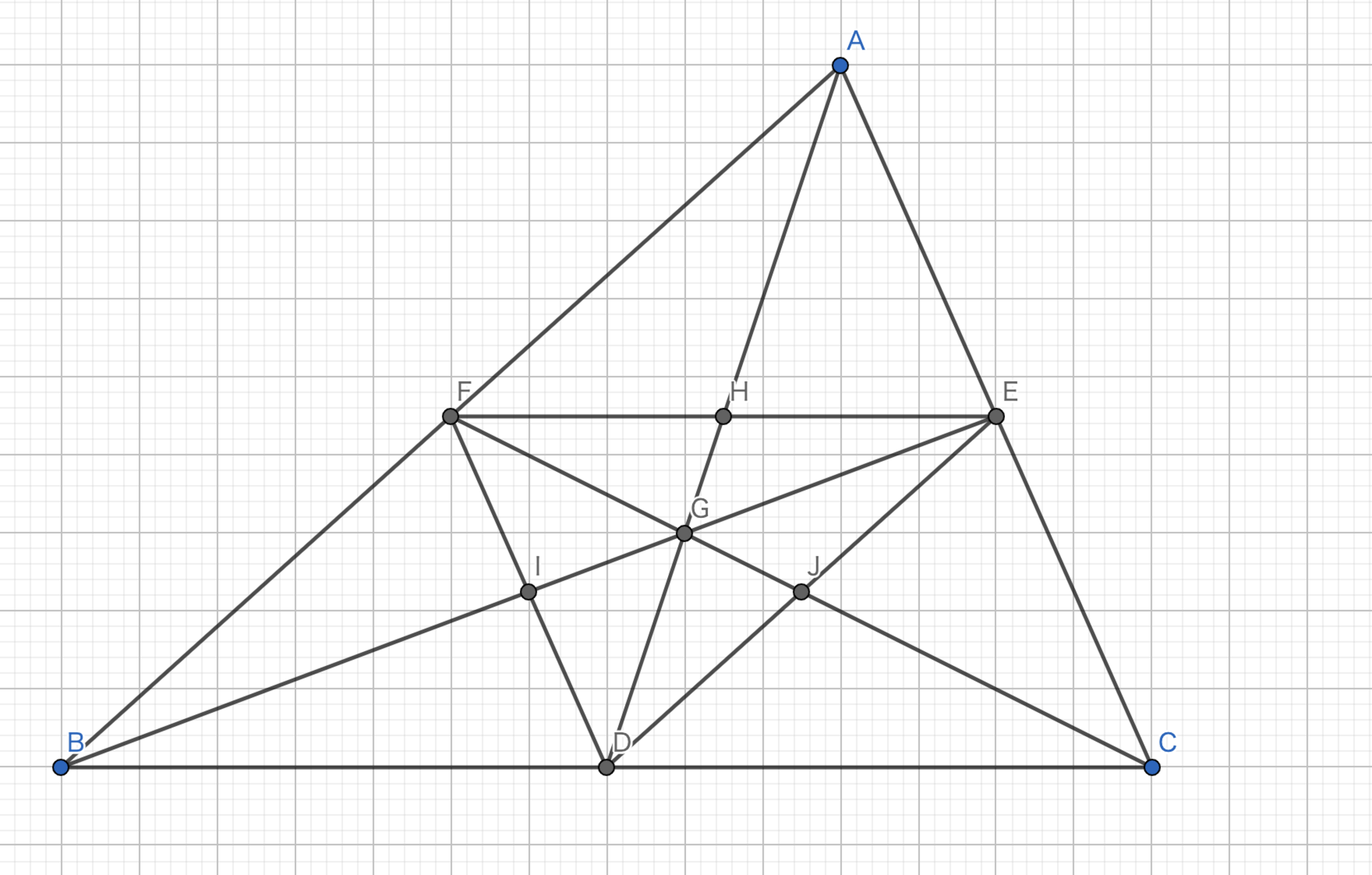 中点三角形の重心-1
中点三角形の重心-1
中点三角形の垂心
中点三角形の垂心は元の三角形の外心と等しい.
中点連結定理より,$EF // BC$であるから$DH \perp BC $である.$DH$は$BC$に垂直であり,中点を通るから垂直二等分線である.同様に,$EI,FJ$も垂直二等分線である.故に,$G$は元の三角形の外心である.
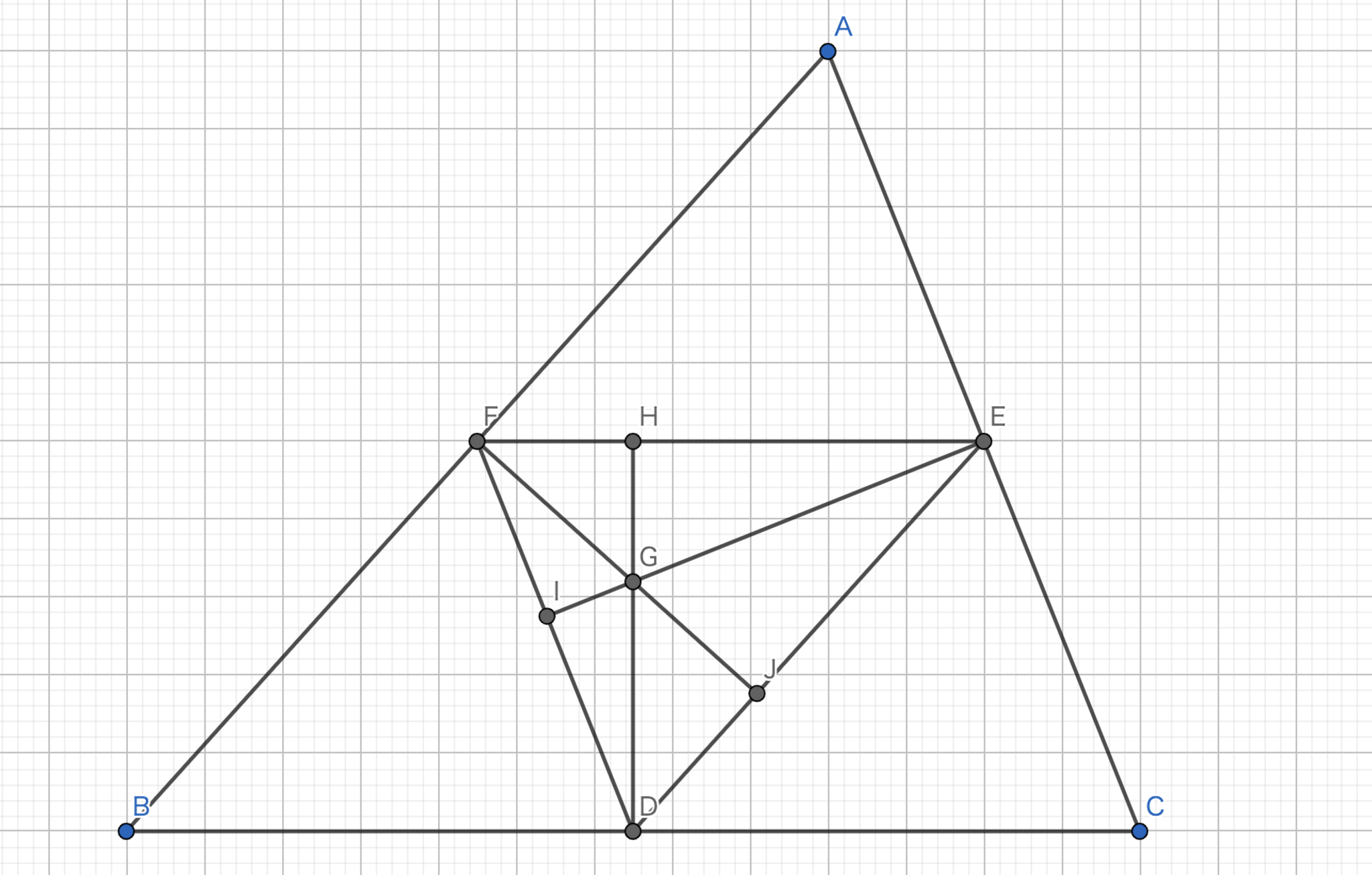 中点三角形の垂心-1
中点三角形の垂心-1
傍心三角形の垂心
傍心三角形の垂心は元の三角形の内心と等しい.
方針:三角形$ABC$の内心が三角形$I_{A}I_{B}I_{C}$の垂心であることを示す.
三角形$ABC$の内心を$I$とする.傍心の存在性より,直線$CI$上に$I_{C}$は存在する.ここで,$\angle{BCI_{A}}=\angle{ACI_{B}}$であり,$I$を内心と仮定していることから,$I_{C}C \perp I_{A}I_{B}$である.同様に,$I_{A}A \perp I_{B}I_{C}$,$I_{B}B \perp I_{C}I_{A}$であるから$I$は三角形$I_{A}I_{B}I_{C}$の垂心である.よって,題意は示された.
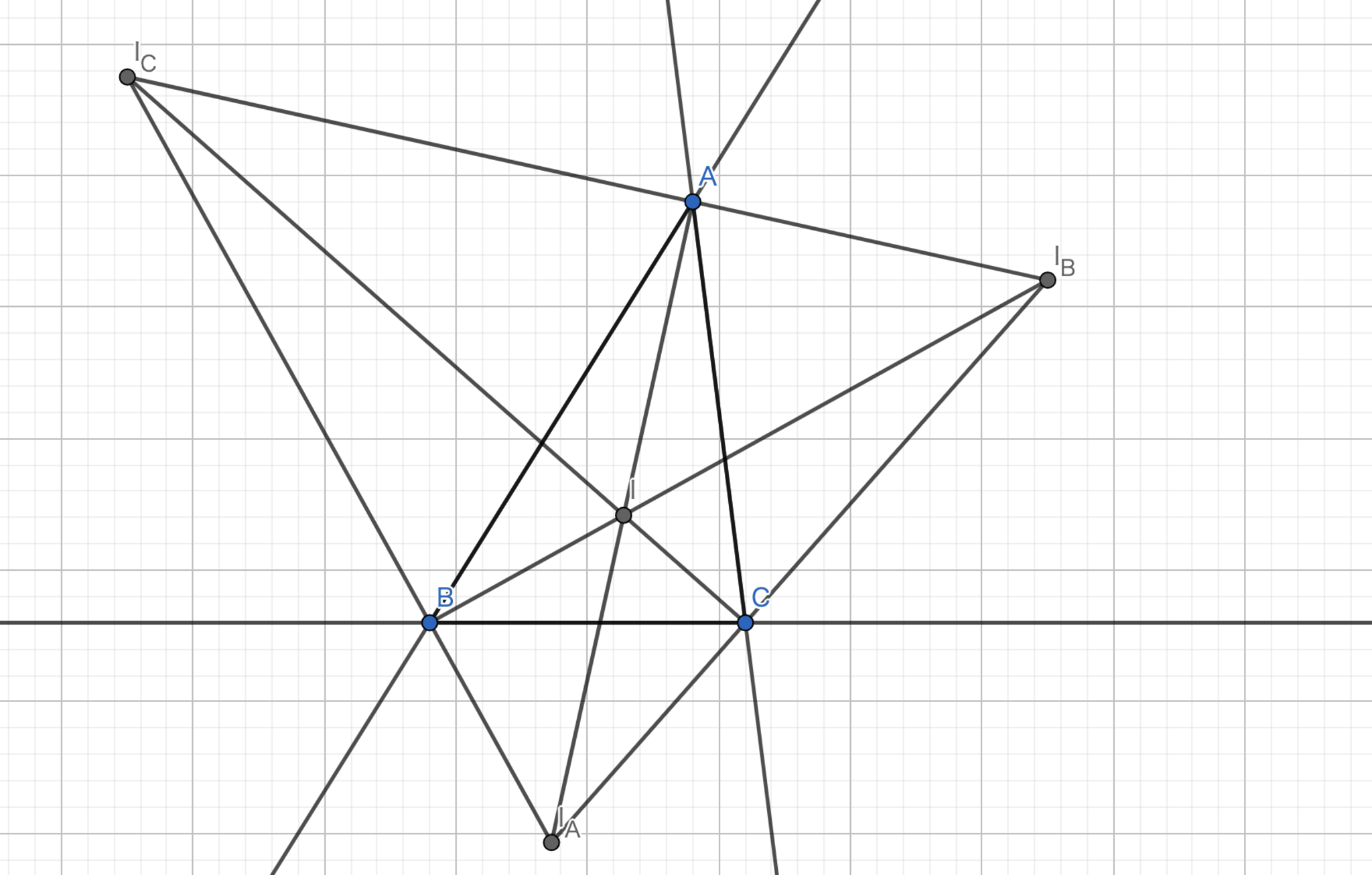 傍心三角形の垂心-1
傍心三角形の垂心-1
垂足三角形の内心
垂足三角形の内心は元の三角形の垂心である.
方針:元の三角形の垂心が垂足三角形の内心であることを示す.共円を利用して,簡単な角度計算で示す.
$\angle{ABC} = x$とする.四角形$AFHE$は共円であるから,$\angle {FEH} = x$である.また,四角形$FBCE$も共円であるから,$\angle {FCB} = x$である.さらに,四角形$CEHD$も共円であるので$\angle {DEH} = x$である.故に,$EB$は$\angle FED$の角の二等分線である.同様に,$FC,DA$も角の二等分線であるから$H$は垂足三角形の内心である.故に題意は示された.
 垂足三角形の内心-1
垂足三角形の内心-1
垂足三角形の傍心
垂足三角形の傍心は元の三角形の各頂点である.
定理18の証明と同様に,$\angle {EFH} = \angle {DFG}$である.また,$\angle {AFE} = 90°-\angle{EFH}$,$\angle{BFD} = 90°-\angle{DFH}$であるから,$\angle {AFE} =\angle{BFD}$である.また,対頂角より$\angle{PFE} = \angle {DFB}$であるから,$\angle{PFA} = \angle{EFA}$である.点$E$に関しても同様.従って,$A$は点$D$に関する三角形$DEF$の傍心である.
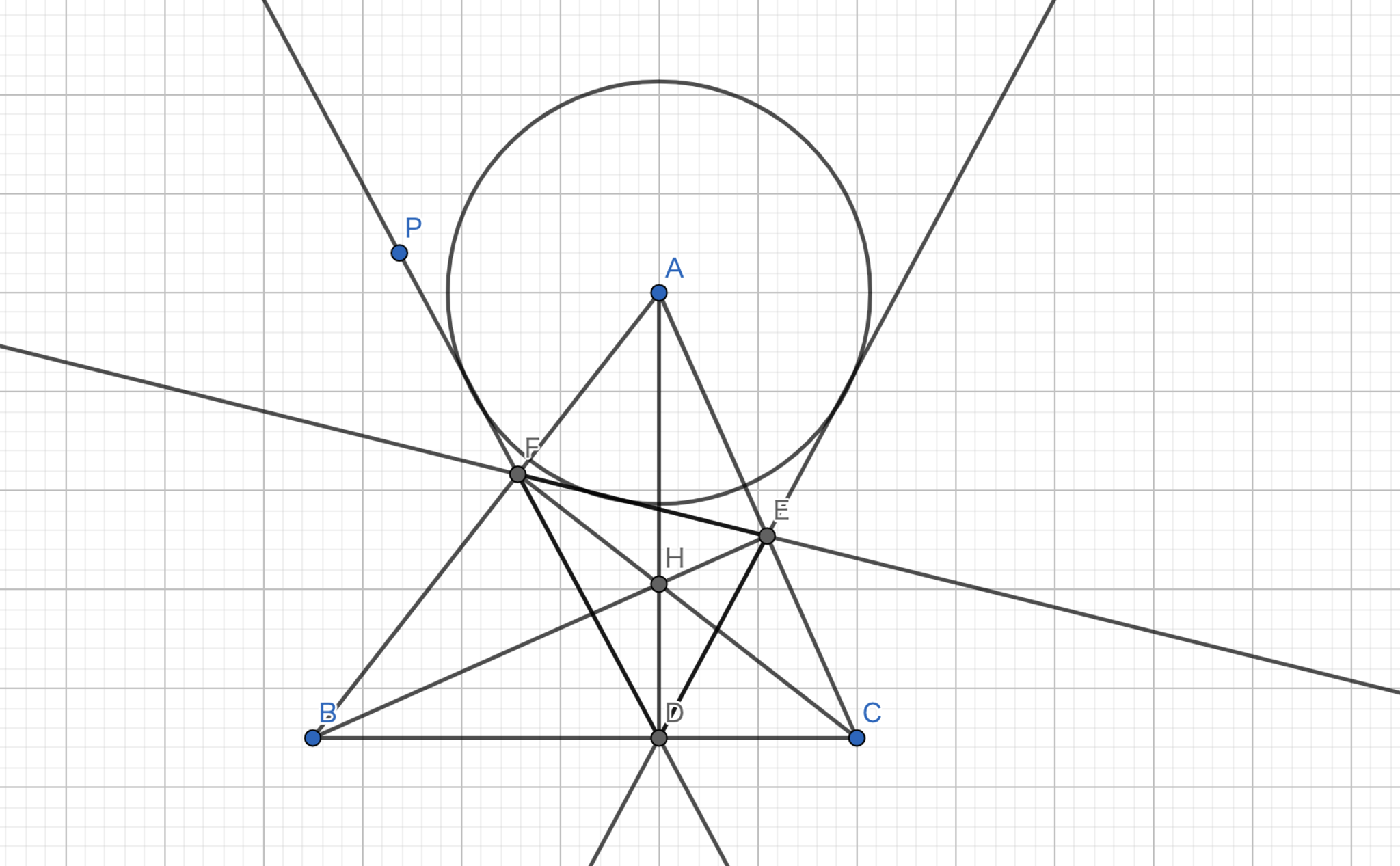 垂足三角形の傍心-1
垂足三角形の傍心-1
ジュルゴンヌ三角形とジュルゴンヌ点の存在
三角形の各頂点と,内接円と対辺の接点を結んだ線分の交点をジュルゴンヌ点という.内接円のと各辺の接点を結んでできた三角形をジュルゴンヌ三角形という.
三角形の各頂点と,内接円と対辺の接点を結んだ線分は一点で交わる.(ジュルゴンヌ点は必ず存在する.)
方針:円外の一点と接点との関係を使う.
$|AE|=|AF|$,$|BF|=|BD|$,$|CD|=|CE|$である.チェバの定理の逆より,$\frac{\left|AF\right|}{\left|FB\right|}\cdot\frac{\left|BD\right|}{\left|DC\right|}\cdot\frac{\left|CE\right|}{\left|EA\right|}=1$であるから一点で交わる.
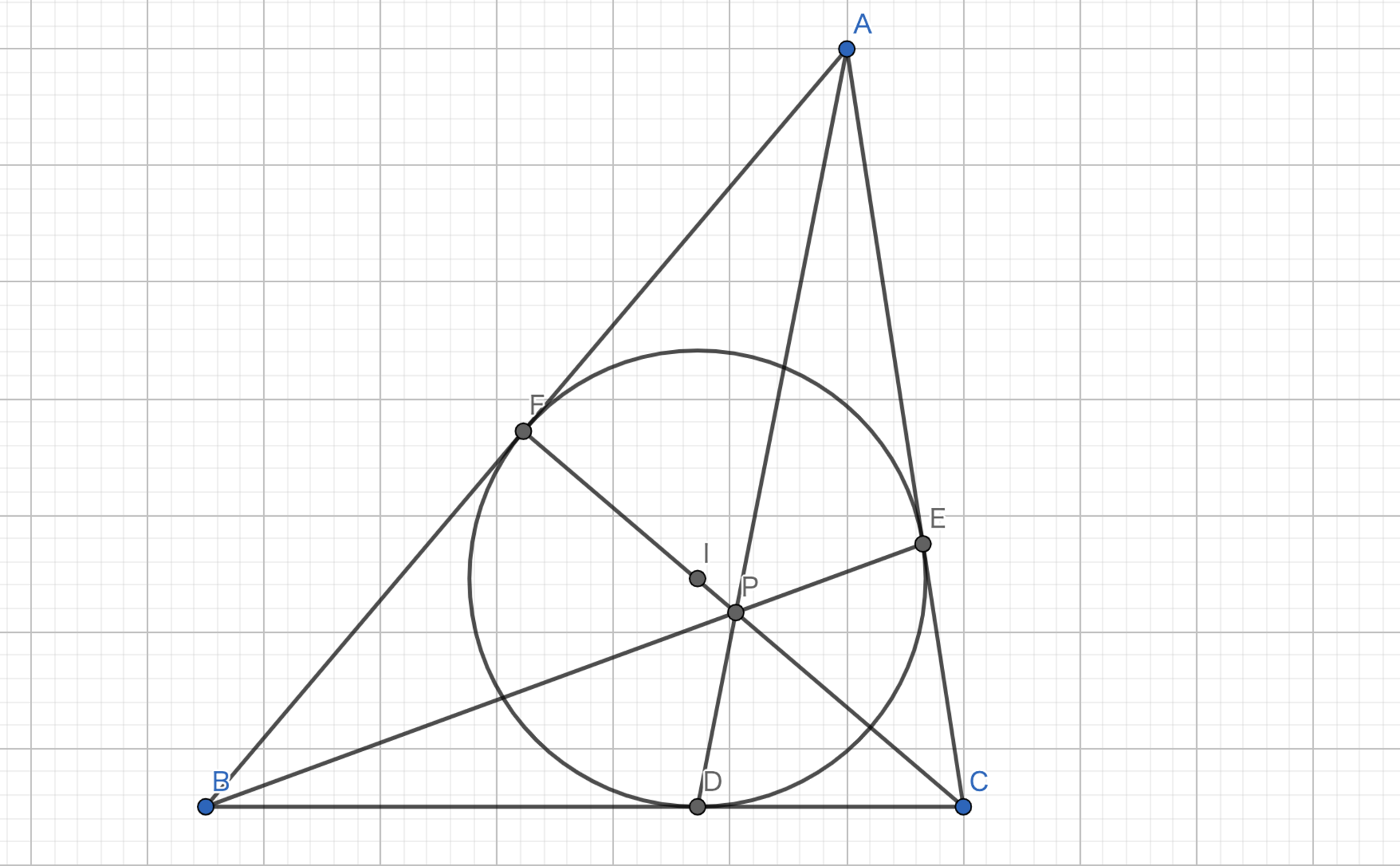 ジュルゴンヌ点-1
ジュルゴンヌ点-1
垂心と外心の等角共役性
垂心と外心は等角共役関係にある.
三角形$OMB$と三角形$OMC$は合同であるので$\angle {BOM} = \angle {COM}$である.また,円周角の定理より$2\angle{BAC} = \angle {BOC}$である.故に,$\angle {BOM} = \angle {COM} = \angle{BAC}$である.これを$α$とする.$\angle{OCB} = 90°-α$である.$\angle {FCA} = 90°-α$である.故に$\angle{ACF} = \angle{BCO}$である.残りの頂点も同様のことが言えるから垂心は外心の等角共役点である.
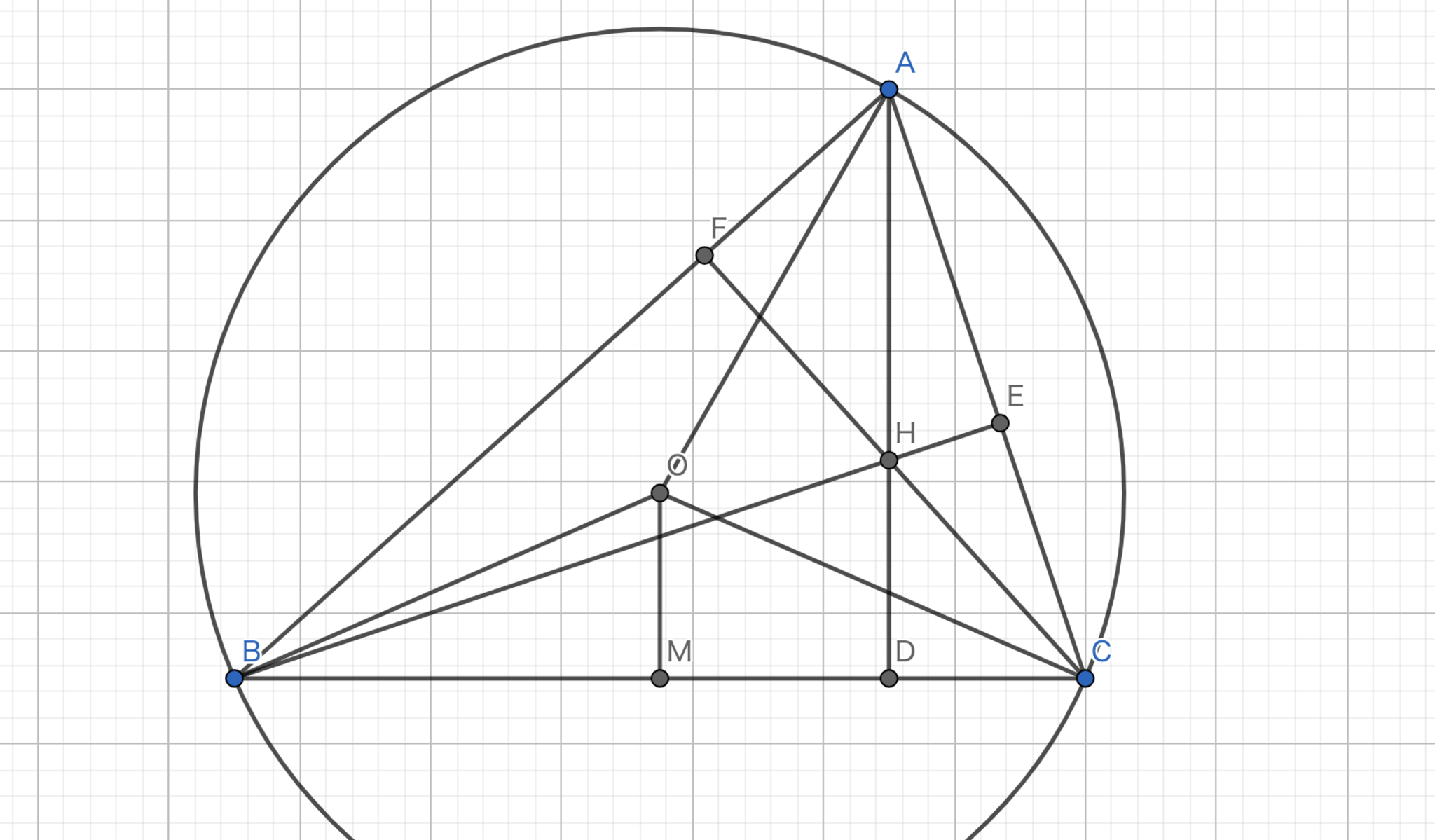 垂心と外心の等角共役性
垂心と外心の等角共役性
内心と外心の距離(オイラーの公式)
内心と外心の距離を$d$,内接円の半径を$r$,外接円の半径を$R$とすると以下の式が成り立つ.
$$
d^{2}=R^{2}-2Rr
$$
方針:方べきの定理を使用する.
$d^{2}=R^{2}-2Rr \Longleftrightarrow (R+d)(R-d)=2Rr$である.$R+d$は$IE$を表していて,$R-d$は$IF$を表している.方べきの定理より,$(R+d)(R-d)=|FI|\cdot |IE|=|AI|\cdot |ID|$である.
$\angle{BCD} = α$とおくと,円周角の定理より,$\angle{BAD} = α$となり,角の二等分線より,$\angle{CAD} = α$も従う.$\angle{ACI}=β$とすると,角の二等分線より$\angle{BCI}=β$である.ここで,$\angle{ICD} = α+β$であり,$\angle{CID} = α+β$であるから三角形$DIC$は二等辺三角形である.これより,$|AI|\cdot |ID| = |AI| \cdot |CD|$である.
三角形$CDH$と三角形$GIA$はそれぞれ直角三角形であり,$\angle{DHC} =\angle{IAG} = α$であるから相似である.ここで三角形$AGI$と三角形$HCD$の相似比を$1:k$とすると,$|AI|\cdot |CD| = |AI| \cdot |GI| \cdot k$となる.また,$ |AI| \cdot |GI| \cdot k = |HD| \cdot |GI|$である.$|HD|= R, |GI| = r$であるから,$d^{2}=R^{2}-2Rr$ である.
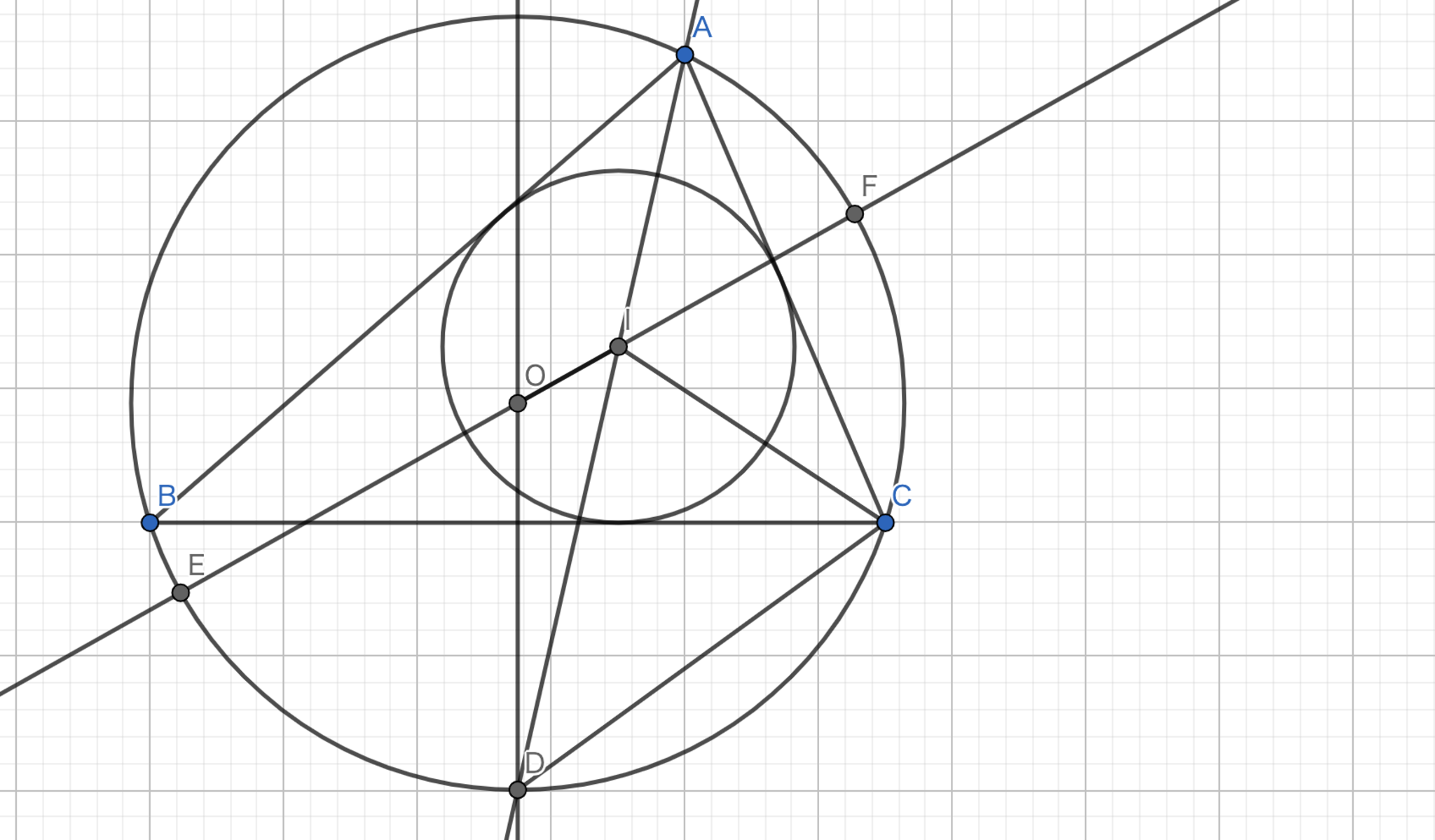 オイラーの公式-1
オイラーの公式-1
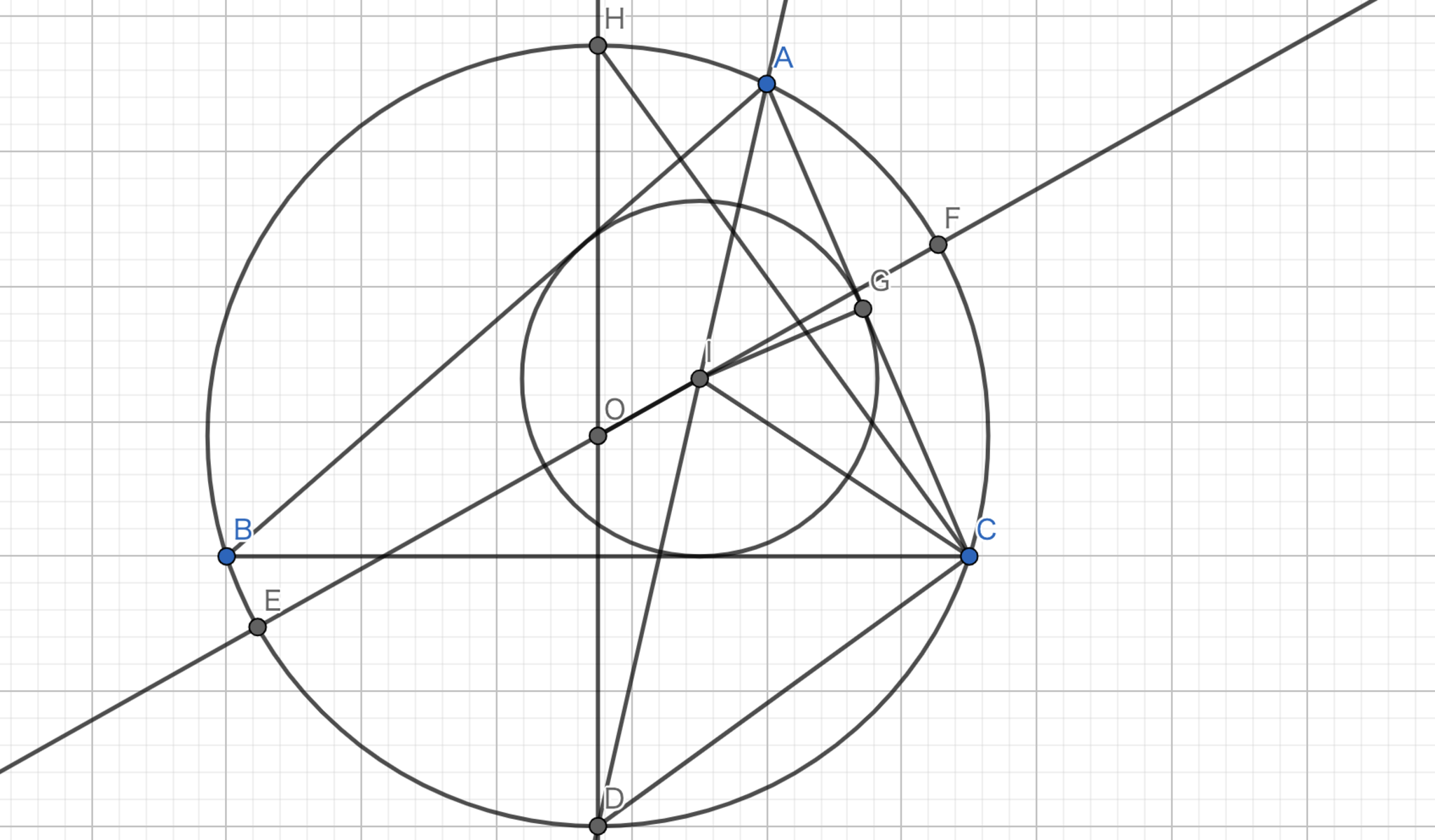 オイラーの公式-2
オイラーの公式-2
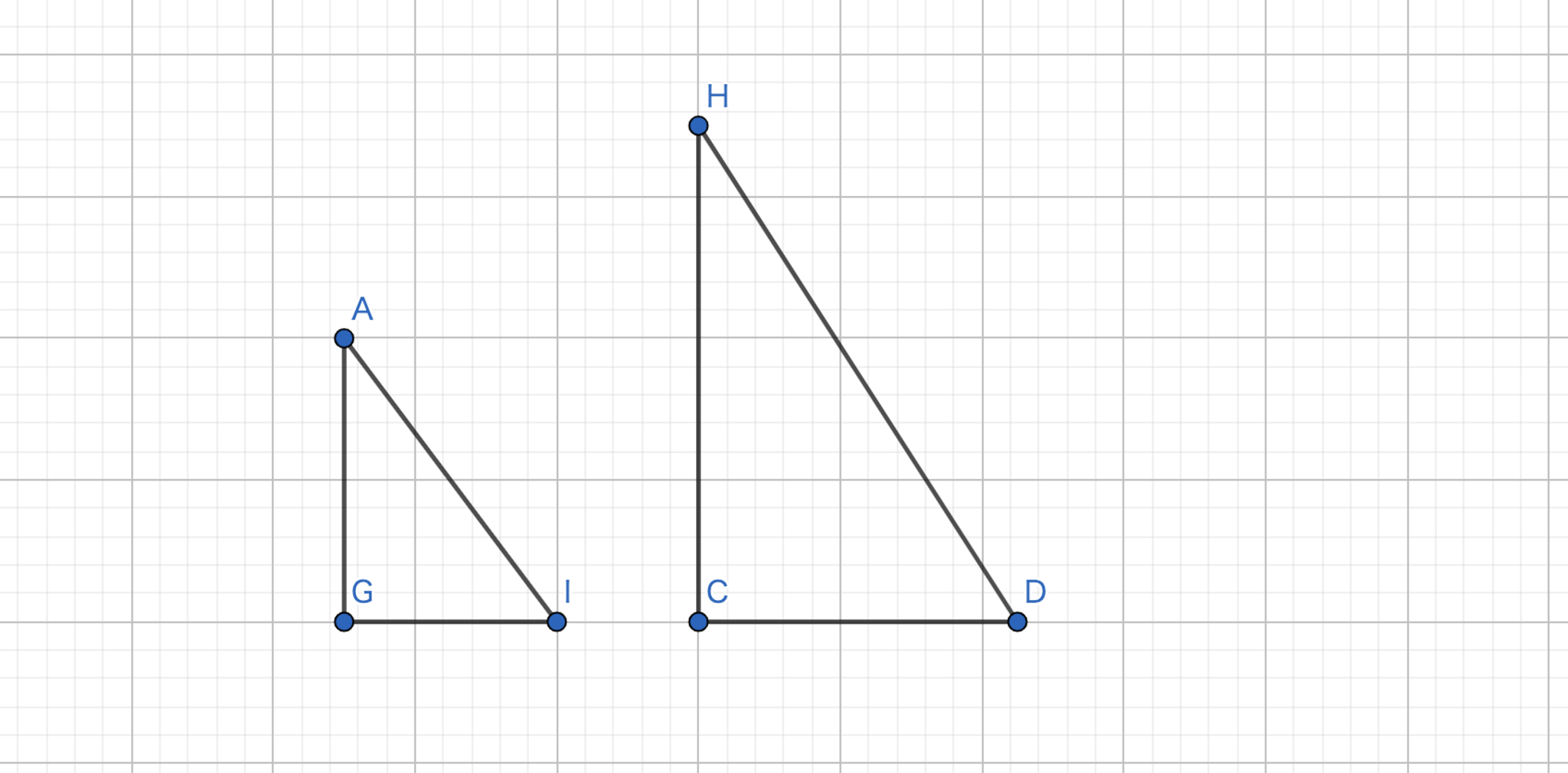 オイラーの公式-3
オイラーの公式-3
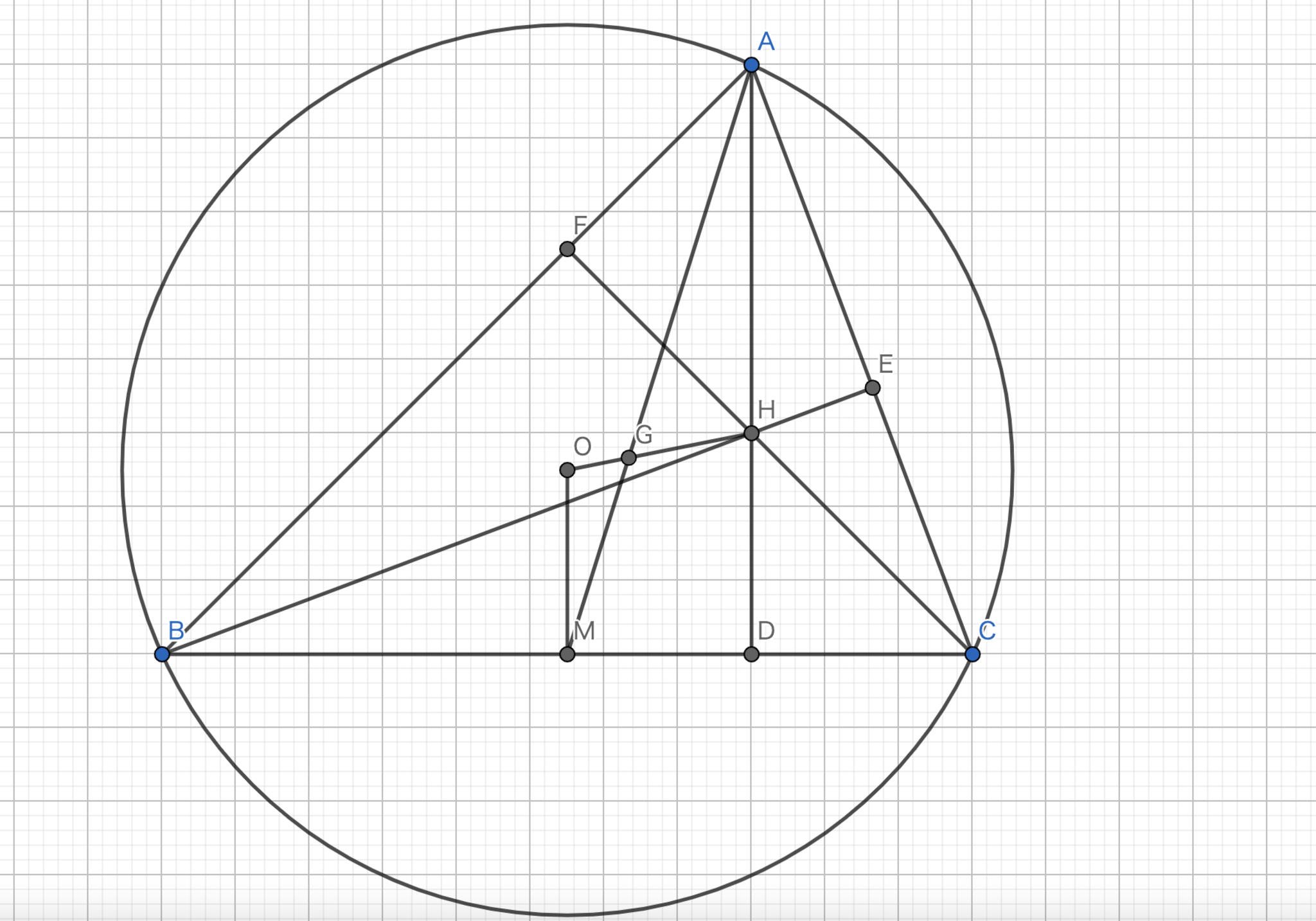
オイラー線
正三角形でない任意の三角形に対して外心,重心,垂心はこの順で一直線に並びその距離の比は$1:2$である.この線のことをオイラー線と呼ぶ.
直線$CO$と円との交点を$P$とする.この時,$CP$は円の直径である.また,$BC$の中点を$M$とすると,中点連結定理より,$OM//PB$であり,$2|OM|=|PB|$である.$ AD\perp BC, PB\perp BC $であるから,$AD // PB$である.また,垂心の性質と円周角の定理より,$ BE\perp AC, PA\perp AC $であるから,$BE//PA$である.よって,四角形$PBHA$は平行四辺形である.よって,$|AH|=|PB|=2|OM|$
図2において,三角形$AGH$と三角形$MGO$は$ \angle MGO = \angle AGH$,$\angle GAH = \angle GMO (\because AD//OM)$であるから,相似である.さらに,$|AH|=2|OM|$より,その相似比は$2:1$である.また,$G$は$AM$を$2:1$に内分する点で$M$が中点であるから$G$は重心である.これより,三点$O,G,H$は一直線条に並び,$|OG|:|GH|=1:2$である.
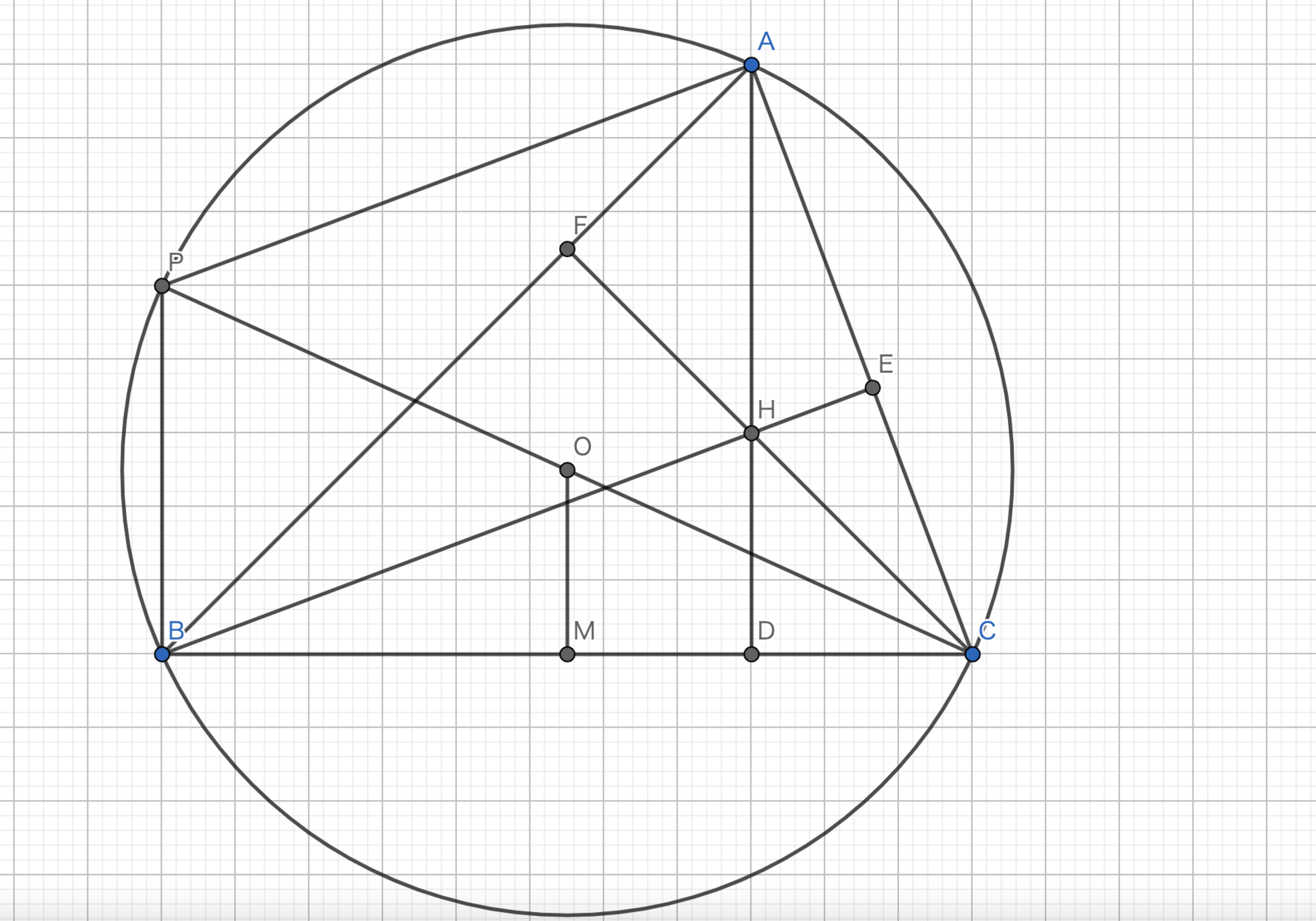 オイラー線-1
オイラー線-1
 オイラー線-2
オイラー線-2
トリリウムの定理
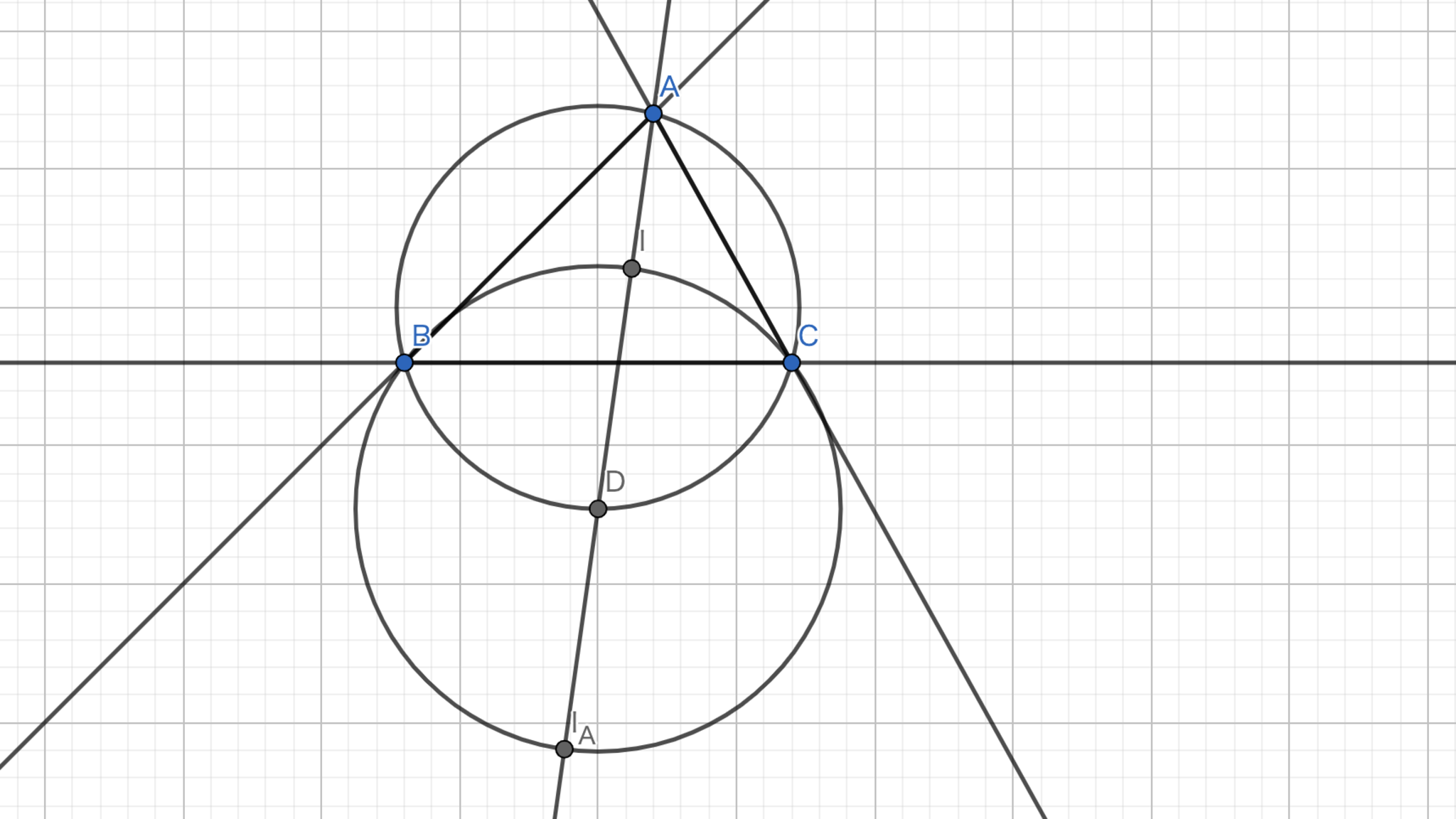
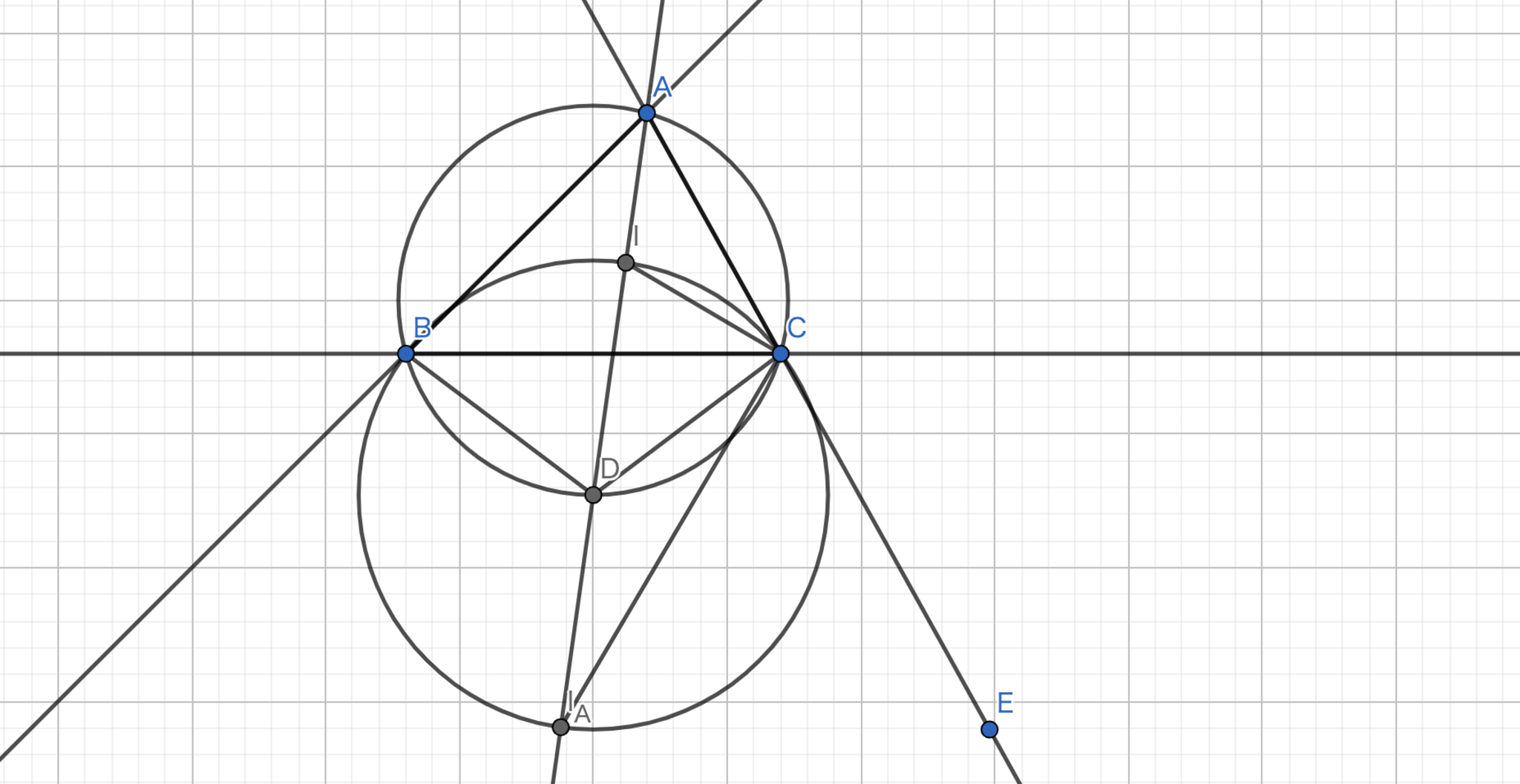
三角形$ABC$の内心を$I$,$A$に関する傍心を$I_{A}$,直線$II_{A}$と三角形$ABC$の外接円との交点のうち$A$でないものを$D$とすれば四点$IBI_{A}C$は$D$を中心とする同一円周上に存在する.
方針:$|ID|=|BD|=|I_{A}D|=|CD|$となることを示す.
円周角の定理より,$\angle{DBC} = \angle {DCB}$であるから$|DB|=|DC|$である.また,$\angle{CID} = \angle{CAI} + \angle{ICA} = \angle {BAD} + \angle {ICB} = \angle {BCD} + \angle{ICB} = \angle{ICD}$であるので$|DI| = |DC|$である.このことから,三点$B,I,C$は$D$を中心とする共円である.よって,ここでは$\angle{ICI_{A}} = 90°$であることを示せば十分である.$\angle{DCI_{A}}=x$とすれば,傍心の性質より$\angle{I_{A}CE} = x+ \angle{BCD}$となる.ここで,$\angle {ACE} = 2\angle{ICB} + 2(\angle{BCI_{A}}) = 180°$であることから,$\angle{ICI_{A}} = \angle{ICB} + (\angle{BCI_{A}}) = 90° $が得られる.よって,円周角の定理の逆より,$II_{A}$は直径であり,$D$が中心であるので,$|ID|=|BD|=|I_{A}D|=|CD|$である.
 トリリウムの定理-1
トリリウムの定理-1
 トリリウムの定理-2
トリリウムの定理-2
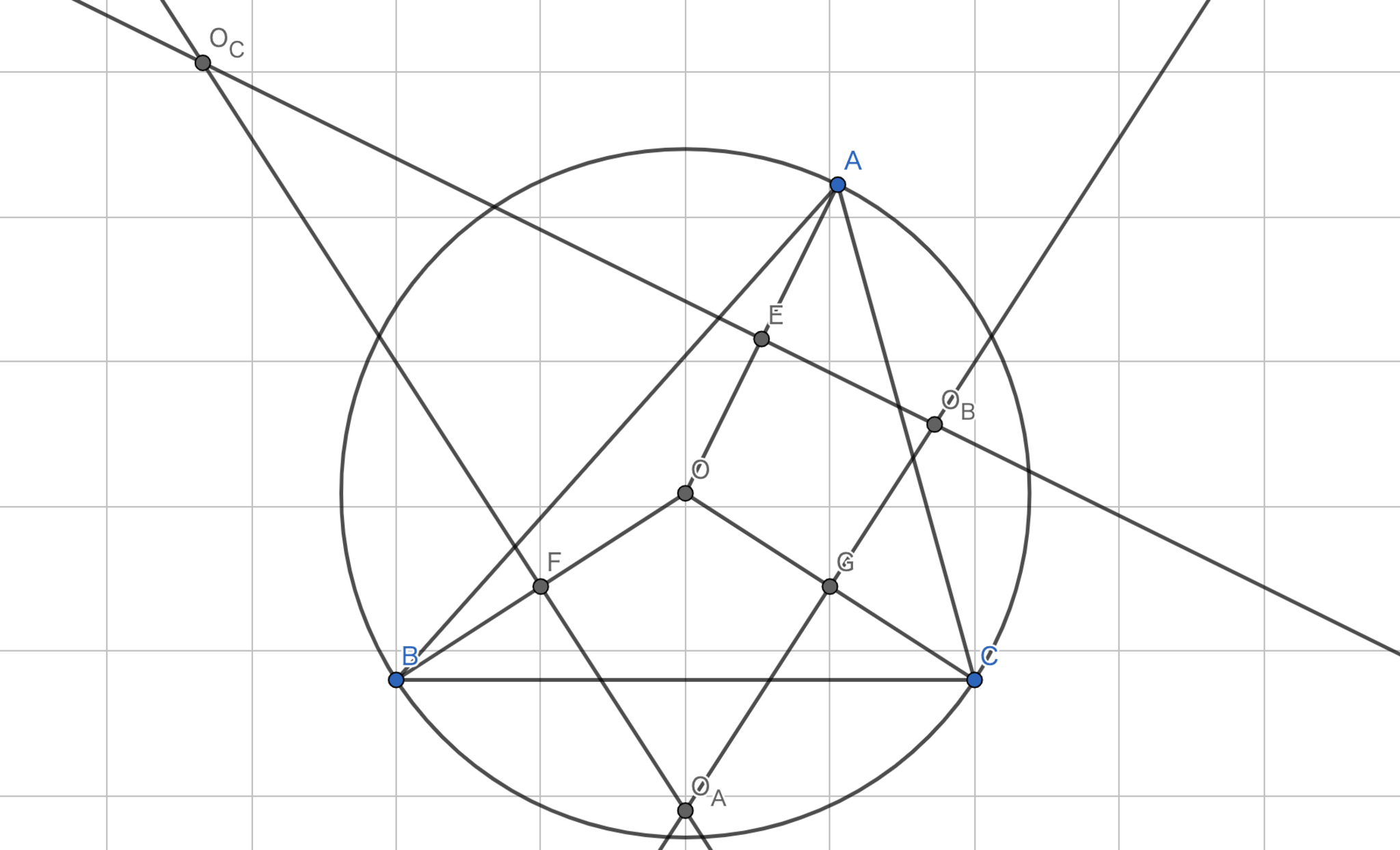
コスニタの定理
三角形$ABC$の外心を$O$として,三角形$OAB,OBC,OCA$の外心を$O_{C},O_{A},O_{B}$とすると,$AO_{A},BO_{B},CO_{C}$は一点で交わる.また,その点は九点円の中心の等角共役点である.
方針:初等的に示すのは難しそうなので複素を利用する.(初等的な証明が思いつきませんでした...)
$A(a),B(b),C(c),O(0)$として,三角形$ABC$の外接円を$|Z|=1$とする.$O_{A}$が$OB$の垂直二等分線と$OC$の垂直二等分線の交点であることを利用して$O_{A}$を求めていく.$OA,OB,OC$の垂直二等分線の式はそれぞれ以下のようになる.
$$
OA:z+a^2\bar{Z} =a \\
OB:z+b^2\bar{Z} =b \\
OC:z+c^2\bar{Z} =c \\
$$
$OA$が再び円と交わるのは$P(\frac{ab+ac-bc}{a-b-c})$である.同様に,$OB$では$Q(\frac{ab+bc-ac}{-a+b-c})$,$OC$は$R(\frac{ac+bc-ab}{-a-b+c})$である.ここで,後述する補題26より$\left(P-b\right)\left(Q-c\right)\left(R-a\right)+\left(c-P\right)\left(a-Q\right)\left(b-R\right)=0$であることを示ばよい.
$$
\begin{align*}
\left(P-b\right)\left(Q-c\right)\left(R-a\right)+\left(c-P\right)\left(a-Q\right)\left(b-R\right) & = \frac{b^{2}+ca}{a-b-c}\cdot\frac{c^{2}+ab}{-a+b-c}\cdot\frac{a^{2}+bc}{-a-b+c}+\frac{-c^{2}-ab}{a-b-c}\cdot\frac{-a^{2}-bc}{-a+b-c}\cdot\frac{-b^{2}+ca}{-a-b+c} \\
& = \frac{\left(b^{2}+ca\right)\left(c^{2}+ab\right)\left(a^{2}+bc\right)+-\left(a^{2}+bc\right)\left(b^{2}+ca\right)\left(c^{2}+ab\right)}{\left(a-b-c\right)\left(-a+b-c\right)\left(-a-b+C\right)} \\
& = 0
\end{align*}
$$
よって題意は示された.
 コスニタの定理-1
コスニタの定理-1
 コスニタの定理-2
コスニタの定理-2
単位円上の六点$a,b,c,d,e,f$において,$ad,be,cf$が共点であるまたは平行であるための必要十分条件は以下のようになる.
$$
\left(a-b\right)\left(c-d\right)\left(e-f\right)+\left(f-a\right)\left(b-c\right)\left(d-e\right)=0
$$
$\Longrightarrow$の証明
(i) 三本が平行である場合
直線$ad,be,cf$はそれぞれ以下のように表される.
$$
z+ad\overline{z}=a+d \\
z+be\overline{z}=b+e \\
z+cf\overline{z}=c+f \\
$$
この時,全て平行であるから,$ad=be=cf$である.$ad=be=cf=x$とすれば,
$$
\begin{align*}
\left(a-b\right)\left(c-d\right)\left(e-f\right)+\left(f-a\right)\left(b-c\right)\left(d-e\right) & = -abd+abe+acd-acf-ade+adf-bce+bcf+bde-bef-\operatorname{cdf}+cef \\
& = -bx+ax+cx-ax-ex+fx-cx+bx+dx-fx-dx+ex \\
& = 0
\end{align*}
$$
となって,成立する.
(ii) 三本が一点で交わる場合
$$
z+ad\overline{z}=a+d \\
z+be\overline{z}=b+e \\
z+cf\overline{z}=c+f \\
$$
であり,これは全て同じ点$W$を通るので
$$
a+d-ad\overline{w}=b+e-be\overline{w}=c+f-cf\overline{w}
$$
となる.一方で,$\left(a-b\right)\left(c-d\right)\left(e-f\right)+\left(f-a\right)\left(b-c\right)\left(d-e\right)=ad(c+f-b-e)+(a+d)(be-cf)-be(c+f)+cf(b+e)$であるから,頑張って計算すると,
$$
\left(a-b\right)\left(c-d\right)\left(e-f\right)+\left(f-a\right)\left(b-c\right)\left(d-e\right) = 0
$$
である.よって,成立する.
$ \Longleftarrow $の証明.
(i) 平行であることの証明
$be,ef$が平行であるときに$ad$も平行であることを示す.$be // cf$だから$ad=be$である.このことを利用して$(a-b)(c-d)(e-f)+(f-a)(b-c)(d-e)$を整理すると,$(ad-be)(c+f-b-e)$であるから,$(a-b)(c-d)(e-f)+(f-a)(b-c)(d-e)=0$より,$ad=be,c+f=b+e$である.$ad=be$の場合は$ad//be$である.また,$c+f=b+e$の時は二つの直線は一致する.よって成立する.
(ii) 一点で交わることの証明
$be,cf$が混じっている時に,$ad$も共点であることを示す.$w$で交わっているとすれば
$$
\begin{align*}
(a-b)(a-d)(e-f)+(f-a)(b-c)(d-e) & = ad(c+f-b-e)+(a+d)(be-cf)-be(c+f)+cf(b+e) \\
& = ad(p+cf \bar{w}-w-be\bar{w})+(a+d)(be-cf)-be(w+cf \bar{w})+cf(w+be\bar{w}) \\
& = (be-cf)(ad \bar{w}-a-d+w) \\
\end{align*}
$$
ここで,$(be-cf)(adw-a-d+w) = 0$であって,$be$と$cf$は平行ではないので,$ad\bar{w}-a-d+w=0$である.故に$w+ad\bar{w} = a+d$である.よって成立する.
よって,題意は示された.
丸山良寛の定理
円に内接する四角形$ABCD$において,三角形$ABC,BCD,CDA,DAB$の内接円の半径を$r_{1},r_{2},r_{3},r_{4}$とすると,$r_{1}+r_{3}=r_{2}+r_{4}$が成り立つ.
方針:内心と外接円がたくさん登場していることからトリリウムの定理を利用する.
弧$AB,BC,CD,DA$の中点を$N,K,L,M$とする.円周角の定理より,$\angle {NMK} + \angle{MNL}=90° $であるから$MK \perp NL$である.ここで,トリリウムの定理より$|MI_{ABD}|=|MI_{ACD}|$である.また円周角の定理より,$\angle{BMK} = \angle{CMK}$であるから,$MK \perp I_{ABD}I_{ACD}$である.よって,$I_{ABD}I_{ACD} // NL$である.同様に内心を$I_{ABC},I_{BCD}$と定めれば$I_{ABD}I_{ABC} // MK, I_{ABC}I_{BCD} // NL , I_{BCD}I_{ACD} // MK$であるから四角形$I_{ABD}I_{ABC}I_{BCD}I_{ACD}$は長方形である.ここで,$I_{ABD}I_{BCD}$と$I_{ABC}I_{ACD}$の交点を$X$とすると,$|I_{ABD}X|=|I_{ABC}X|=|I_{BCD}X|=|I_{ACD}X|$となる.またこの長さを$x$とする.三角形$OI_{ABD}I_{BCD}$で中線定理を用いると,$|OI_{ABD}|^2+|OI_{BCD}|^2=2(|OX|^2+x^2)$となる.同様に,三角形$OI_{ABC}I_{CDA}$についても中線定理を適用すると,$|OI_{ABC}|^2+|OI_{CDA}|^2=2(|OX|^2+x^2)$となる.このことから,$|OI_{ABD}|^2+|OI_{BCD}|^2=|OI_{ABC}|^2+|OI_{CDA}|^2$が得られる.ここで,オイラーの定理を用いて,$d^2=R^2-2Rr$をそれぞれ代入する.全て同様の円に内接するので外接円の半径$R$は等しい.従って$R^2-2Rr_1+R^2-2Rr_3=R^2-2Rr_2+R^2-2Rr_4$が得られる.よって,$r_{1}+r_{3}=r_{2}+r_{4}$である. (2022/08/07一部追記)
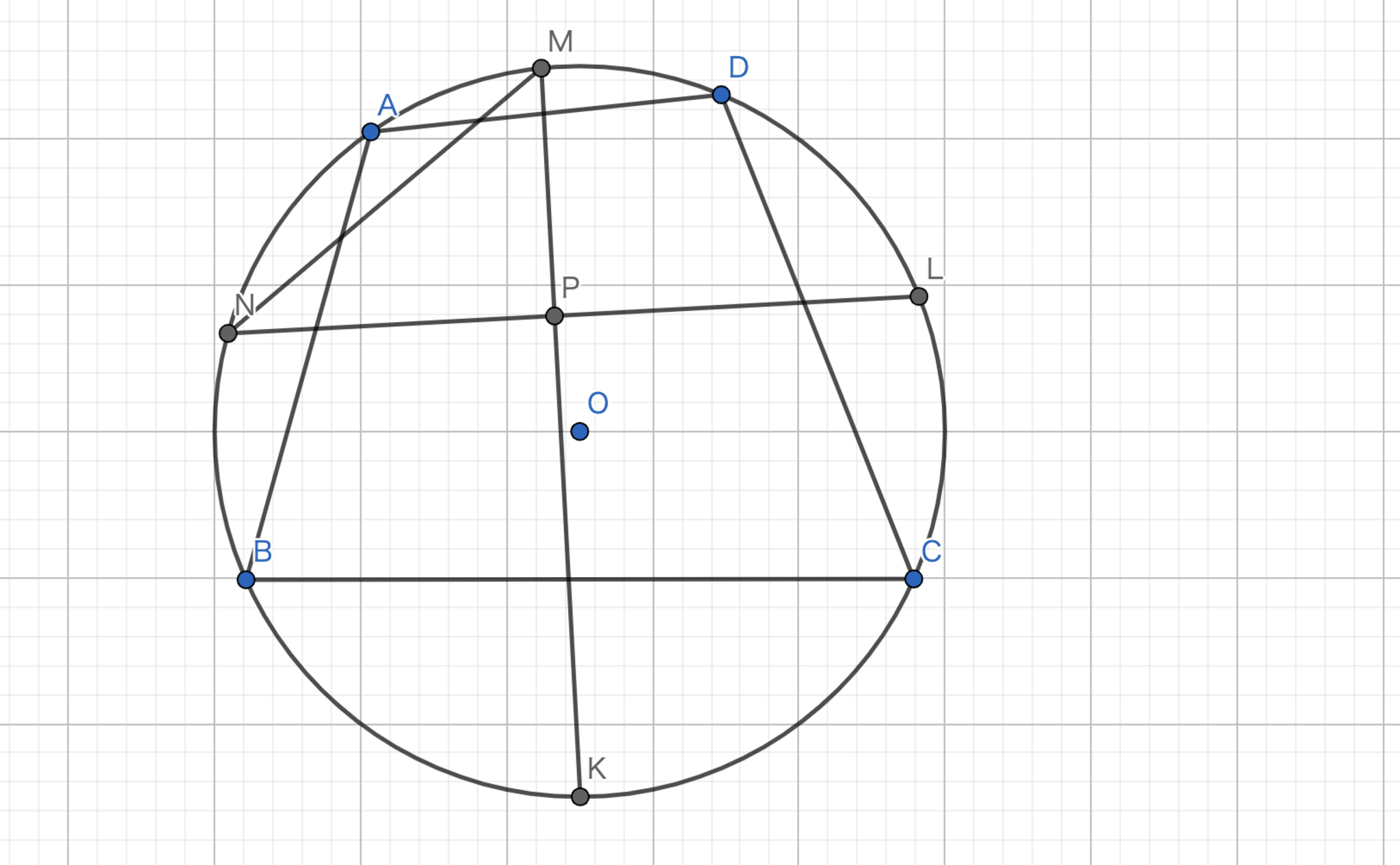 丸山良寛の定理-1
丸山良寛の定理-1
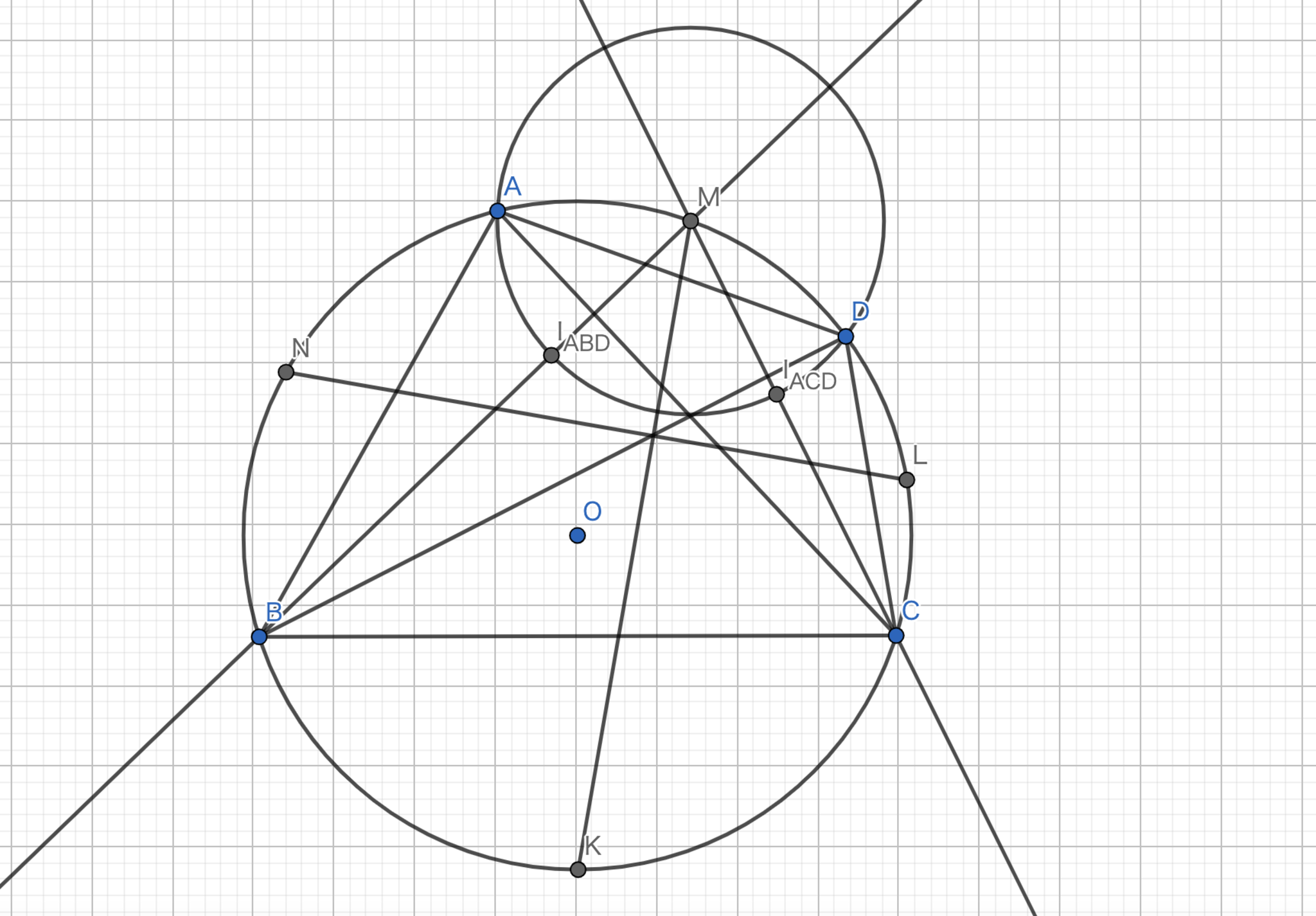 丸山良寛の定理-2
丸山良寛の定理-2
利用例
利用例は挙げたらキリがないですが,ここでは特に五心の基本的な性質と深く関わっている問題をいくつか集めてみました.是非考えてみてください.
$AB \neq AC$なる鋭角三角形$ABC$があり,$A$から$BC$に降ろした垂線の足を$H$とおく.点$P,Q$を三点$A,B,P$と三点$A,C,Q$がともにこの順に一直線状になるように並ぶようにとると,$HP=HQ$が成り立った.このとき,$H$は三角形$APQ$の外心であることを示せ.
$\angle{B}=60°$を満たす三角形$ABC$の垂心を$H$,内心を$I$とする.三角形$AHC$の外心を$O$とする.この時,以下の命題を示せ.
- 三点$B,I,O$は同一直線上に存在する.
- $O$は三角形$ABC$の外接円上に存在する.
簡単ではありますが,自作問題なので一応解説をおいておきます.
- 円周角の定理より,$\angle{AO'C}=120°$.また,$\angle{AIC}=60°+\frac{180°-60°}{2}=120°$である.$A$から$BC$へ降ろした垂線の足と$C$から$BA$に降ろした垂線の足と$A,H$は共円であるから,$\angle{AHC}=120°$である.よって,五点$AHIO'C$は共円である.よって,$O$は$O'H$の垂直二等分線上に存在する.
一方で,垂心と外心の等角共役性より,$\angle{O'BA}=\angle{HBC}$である.また,$I$は内心なので$\angle{IBA}=\angle{IBC}$となる.このことから,$\angle{IBH}=\angle{IBO'} \cdots ①$が従う.また,$H$から$AB$へと降ろした垂線の足を$P$として,線分$BC$の中点を$M$とすると,三角形$PBC$は$|PB|:|CB|=1:2$,特に$|PB|=|MB|$を満たすような直角三角形となる.$|PB|=|MB|$,$\angle{O'BM}=\angle{HBP}$,$\angle{O'MB}=\angle{HPB}=90°$より,$\triangle{HPB} \equiv \triangle{O'MB}$となる.よって,$|BO'|=|BH| \cdots ②$となる.①,②より,$B,I$は線分$O'H$の垂直二等分線上に存在する.以上より,三点$B,I,O$は線分$O'H$の垂直二等分線上に存在する事が示された.
- 示すことは三角形$OO'C$が正三角形であることと同値である.$\angle{OO'C}=60°$であり,$O$は$\triangle{O'CA}$の外心であるから$|OC|=|OO'|$である.よって,三角形$OO'C$は正三角形であるから題意は示された.
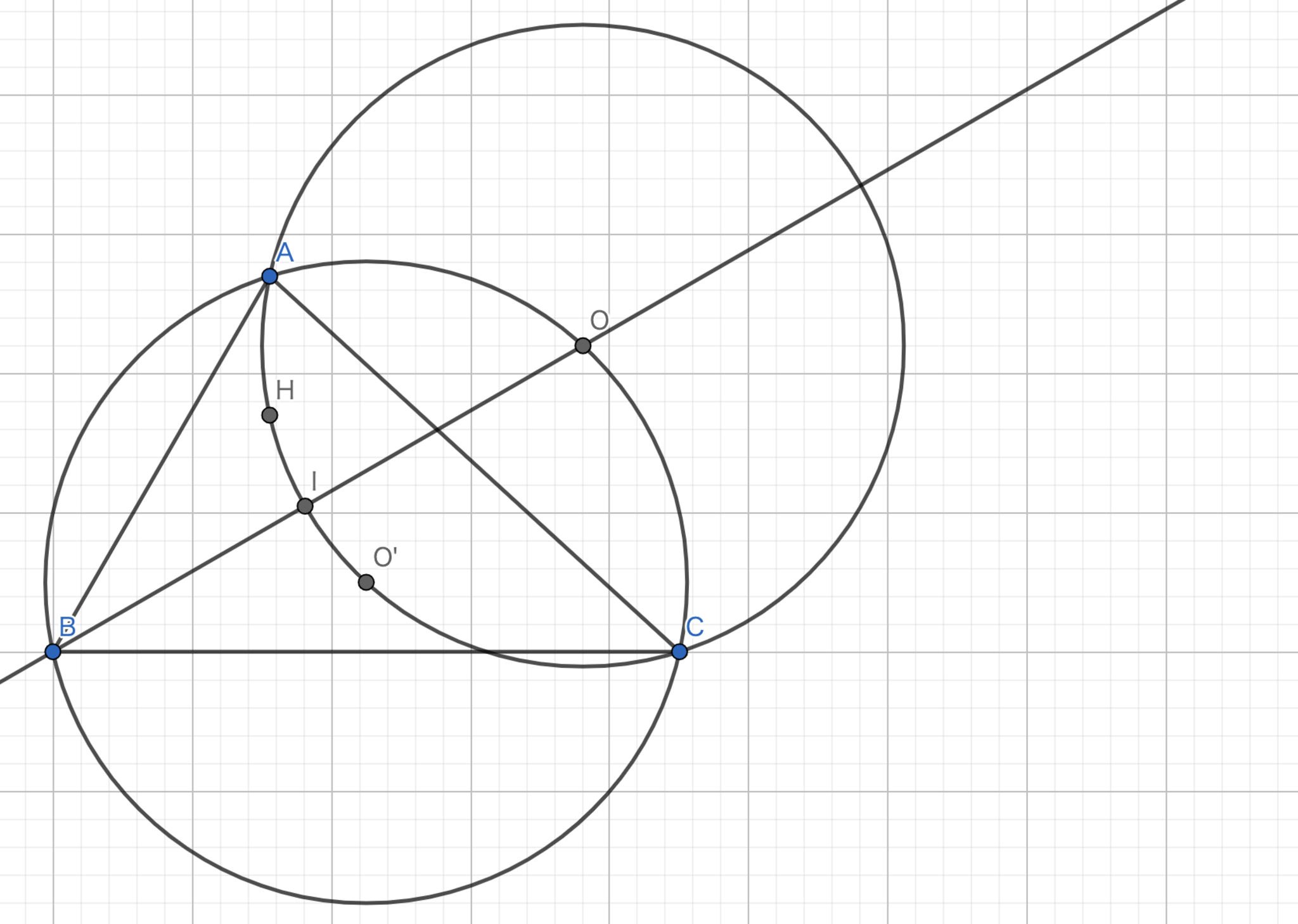 問題文の状況を書き起こしただけの図
問題文の状況を書き起こしただけの図
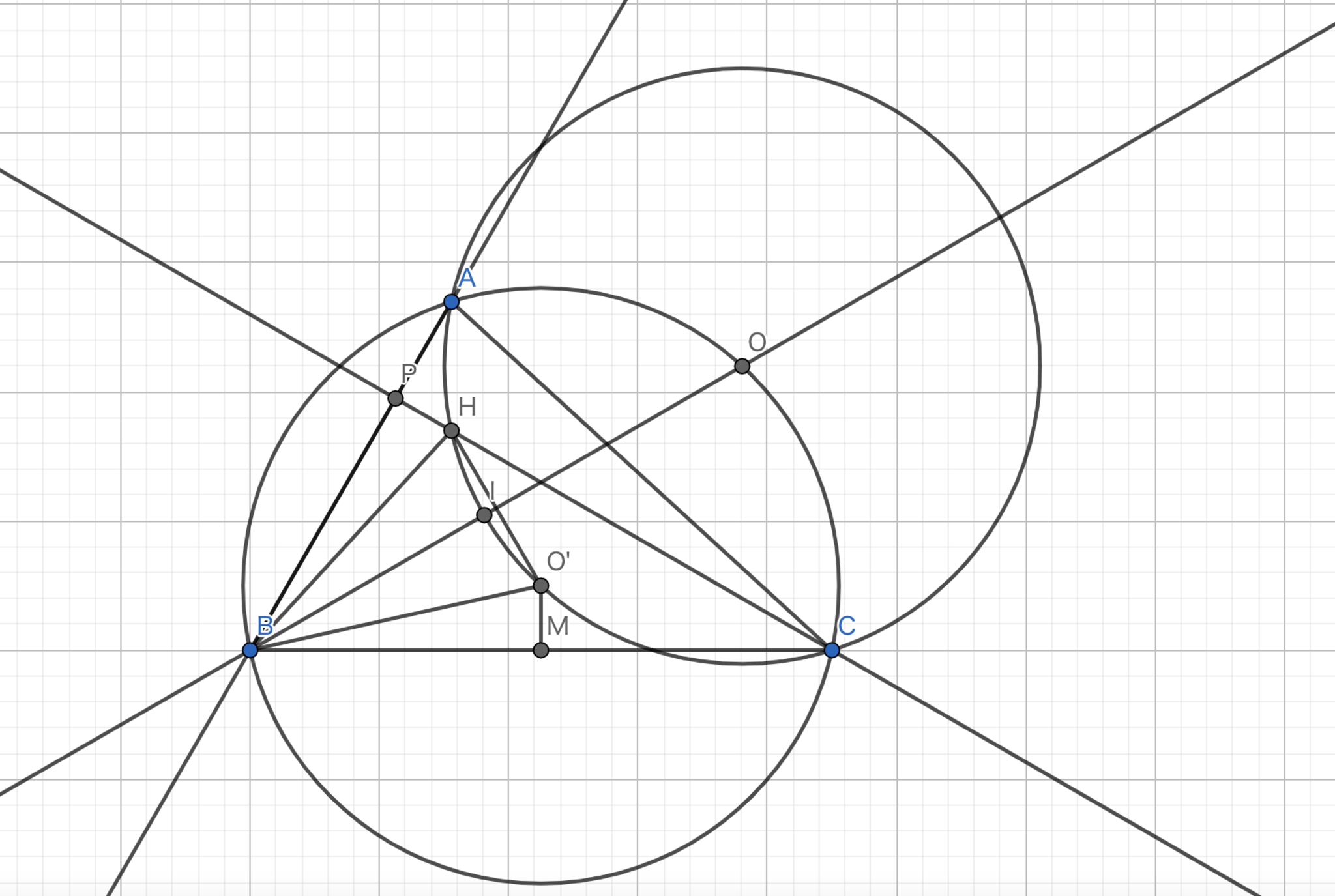 (1)の図
(1)の図
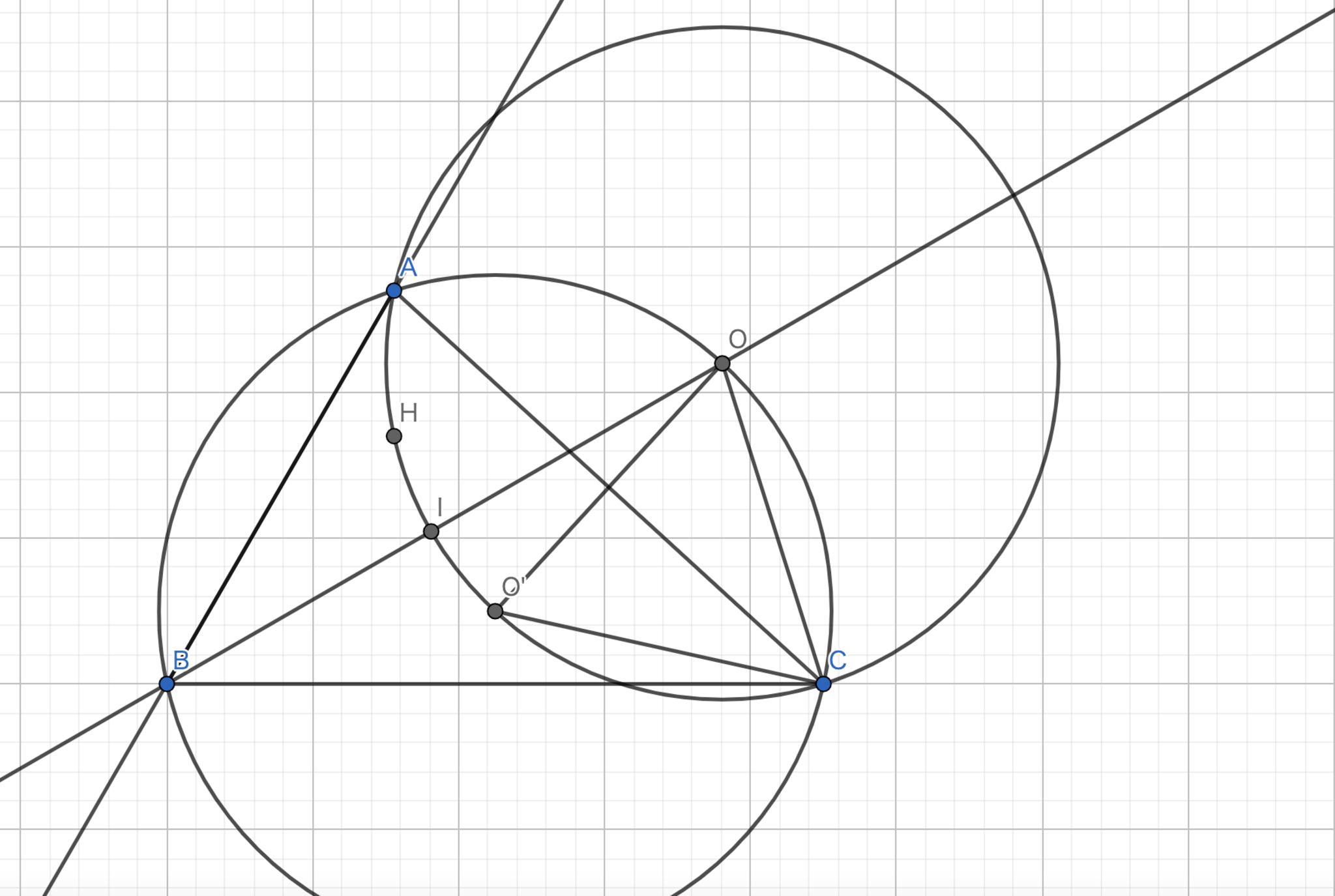 (2)の図
(2)の図
終わりに
とても長い記事となってしまいましたが五心の基本性質を全て網羅できた気がします.作問するときに見たりと活用していただけると嬉しいです!!
