(自己紹介と) 自作問題の解説

955

こんにちは，locker といいます．中３です．
主に競技数学をやっています．OMC に作問を投げたりもします．
なんとなくアカウントを作ったので，記事投稿はそんなにしないと思います．

とは言えこれだけで終わるとあれなので問題の解説でもします．どっちかというとこっちが本編です．解説する問題は twitter の作問リレーで私が出したものです．

ウォーミングアップ

いったん，私が中２の頃に出題した次の問題を考えましょう．今回の本題はこの問題をリメイクする形で作りました．

以下の値が整数となることを示せ．
$\frac{(100!)^{50}}{1^{100} \times 2^{99} \times \dots \times 100^{1}}$

分母がなんか気持ち悪いですが，次のような図を縦と横から見ることを考えると
$1! \times 2! \times \dots \times 100!$
と変形できます：
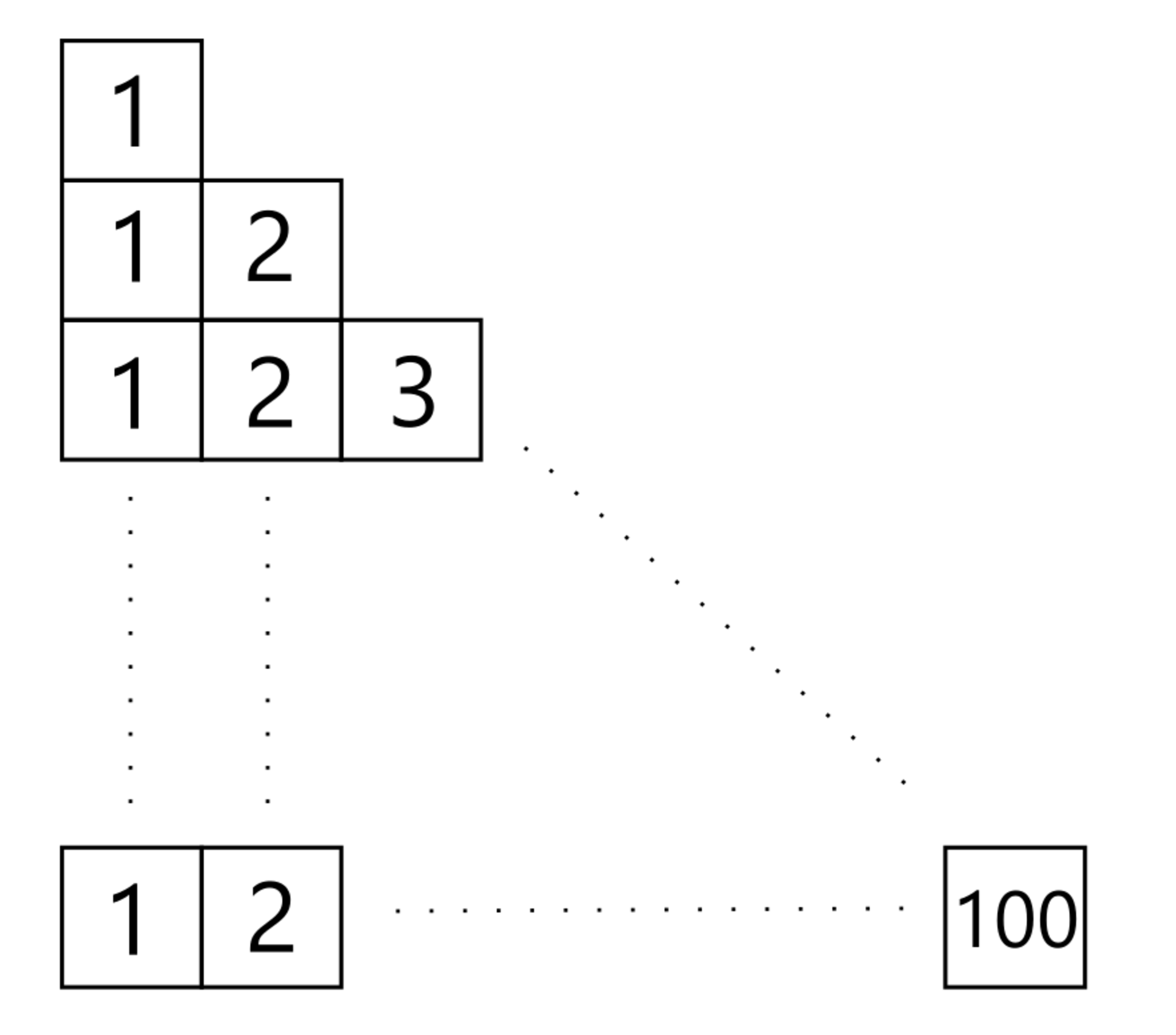1^100×2^99×...×100^1 の図
これで分母，分子の両方が階乗で表されたので，なんか二項係数っぽい感じがしますね．実際
$\begin{aligned} \frac{(100!)^{50}}{1! \times 2! \times \dots \times 100!} & = \frac{100!}{1! \times 100!} \times \frac{100!}{2! \times 99!} \times \dots \times \frac{100!}{50! \times 51!} \\ = \frac{_{101} C_{1}}{101} \times \frac{_{101} C_{2}}{101} \times \dots \times \frac{_{101} C_{50}}{101} \end{aligned}$
と変形でき， $_{101} C_{1},_{101} C_{2}, \dots,_{101} C_{50}$ は整数かつ，全て素数 $101$ の倍数なので，示されました．

本題

$(1, 2, \dots, 100)$ の並べ替え $(a_{1}, a_{2}, \dots, a_{100})$ が任意の $1 \leq k \leq 100$ について以下を満たしている：

$a_{i} > a_{k}$ なる $i$ が全て $k$ より大きい，または全て $k$ より小さい．

このような $(a_{1}, a_{2}, \dots, a_{100})$ について，以下の値が整数となることを示せ．
${(\frac{1}{101 - a_{1}})}^{a_{1}} {(\frac{2}{101 - a_{2}})}^{a_{2}} \dots {(\frac{100}{101 - a_{100}})}^{a_{100}}$

問題１と問題２に共通するのは，二項係数をうまく使って示すという点です．

とりあえず展開して，分母を先ほどと同様に整理すると
$\frac{1^{a_{1}} \times 2^{a_{2}} \times \dots \times 100^{a_{100}}}{1! \times 2! \times \dots \times 100!}$
が整数であること，つまり
$1^{a_{1}} \times 2^{a_{2}} \times \dots \times 100^{a_{100}}$
が $1! \times 2! \times \dots \times 100!$ の倍数であることを示せばいいです．

次に $a_{n}$ について探っていきます．条件を言い換えれば， $a_{n}$ は次のようにして構成できることが分かります．

最初に $100$ のみがある状態を作る．
$99$ を最左または最右に並べる．
$98$ を最左または最右に並べる．
...
$1$ を最左または最右に並べる．

つまり
$(100)$ → (右に並べる) → $(100, 99)$ → (左に並べる) → $(98, 100, 99)$ → (右に並べる) → $(98, 100, 99, 97)$ → ...
というようにして $a_{1}, a_{2}, \dots, a_{100}$ が作れるということです．

さて，ここで以下のように $1^{a_{1}} \times 2^{a_{2}} \times \dots \times 100^{a_{100}}$ の図を描いてみましょう．ただし，下図では $100$ を $5$ に変換しています．
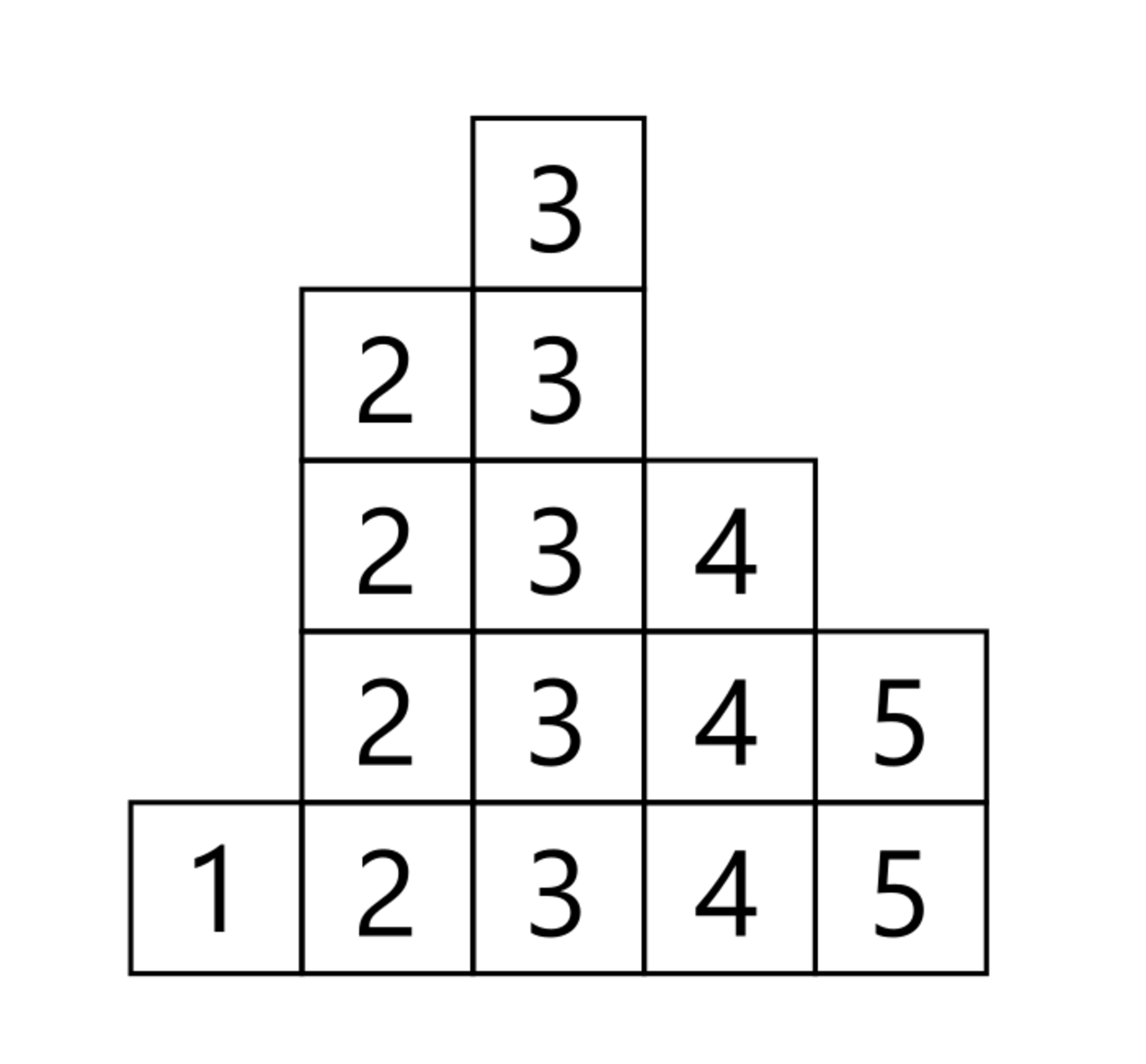1^(a1)×2^(a2)×...×100^(a100) の図
そしてこれを上の段から順番に見てみます．すると，連続する $1, 2, \dots, 100$ 個の整数が現れます．
これはさっき述べた性質から簡単に確認できます． $100$ ， $99$ と $100$ ， $98$ と $99$ と $100$ ，... はすべて連続して $a_{n}$ の中に現れるからです．

もう分かった方が多いのではないでしょうか．分子は上で述べた理由から
( $1$ 個の連続する整数の積) $\times$ ( $2$ 個の連続する整数の積) $\times \dots \times$ ( $100$ 個の連続する整数の積)
と表せます．ここで二項係数が整数であることから，これらは左から順番に $1!, 2!, \dots, 100!$ で割り切れます．従って $1^{a_{1}} \times 2^{a_{2}} \times \dots \times 100^{a_{100}}$ は $1! \times 2! \times \dots \times 100!$ の倍数となり，題意は示されました．

投稿日：2022年8月6日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

locker

5185

2008年の早生まれです

他の人のコメント

コメントはありません。

読み込み中

locker

(自己紹介と) 自作問題の解説

ウォーミングアップ
本題