文献あり

Symmedianまとめ(類似中線)

4625

初めに

今回は競技数学の幾何の重要な知識のSymmedianについてまとめていきたいと思います.Symmedianは幾何の知識をフル活用する最高の題材です!!Symmedianはなかなか知識がまとめられているサイトが少なかったので少しでも参考になれば良いなと思います.(あくまでもまとめノートです.正確性は保証できませんので間違いがあったら訂正していただけると助かります.)

注意の見出し

本記事に修正、加筆を加えた最新版もぜひご覧ください。

Symmedianとは

Symmedian

中線の等角共役線をSymmedianと呼ぶ.図において, $A M, A D$ はそれぞれ中線とSymmedianであり, $∠ B A M = ∠ C A D$ である.

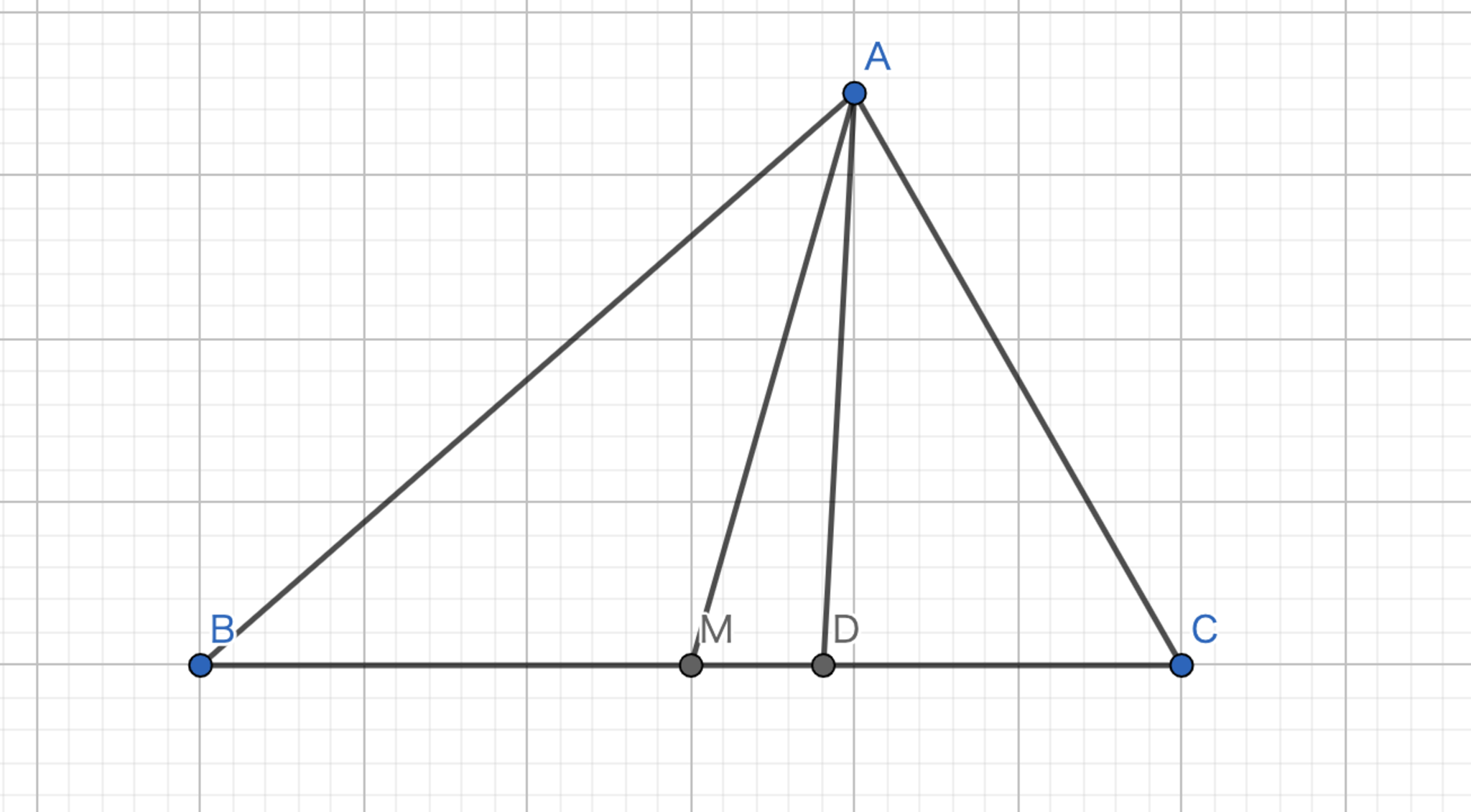Symmedian-def

Symmedianの作図

定規とコンパスだけで等角共役線を作図する一般的な方法はありません.まずはSymmedianを作図する方法を考えてみましょう.

2022/08/08追記:嘘つきました.等角共役線は作図可能です.

Symmedianの作図

三角形 $A B C$ の外接円の $B, C$ における接線の交点を $P$ とすれば $A P$ は三角形 $A B C$ のSymmedianとなる.

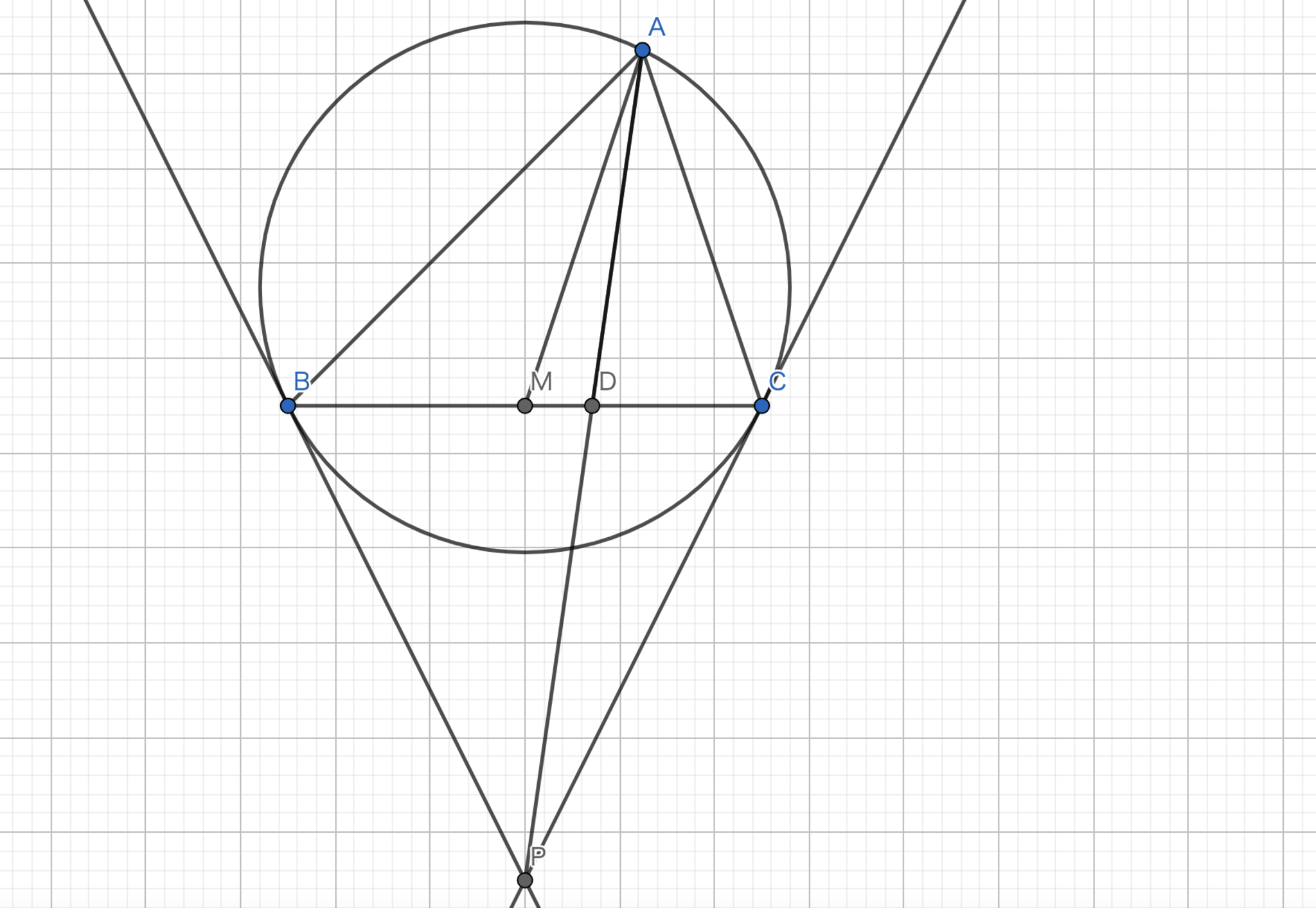Symmedian-作図1

まずは,これでSymmedianが作図できていることを確かめていきましょう.幾何の良い練習問題になると思うので知らない人は一度自分で考えてみてください！！

方針:三角形 $A B D$ と三角形 $A M C$ の相似を示す.

$M$ を $B C$ の中点, $H$ を $A D$ の中点とする.
まずはわかる共円を発見するところから始めていきましょう。 $∠ O B P = ∠ O C P = 90 °$ より,4点 $O, B, P, C$ は共円である.また,中心と弦への中点を結ぶ直線と弦は垂直に交わるから $∠ O H A = 90 °$ である.したがって, $B, P, C, H, O$ は共円である.これより, $∠ C H P = ∠ C O P = ∠ B A C$ がしたがう.また, $∠ B H D = ∠ B A C$ も得られる.一方で,円周角の定理より, $∠ B D H = ∠ B C A$ である.以上より, $△ A B C ∽ △ H B D$ である.このことから, $| B D | : | D H | = | B C | : | C A |$ が得られる.さらに, $H$ が $A D$ の中点, $M$ が $B C$ の中点であることを利用すると, $| B D | : | D A | = | M C | : | C A |$ が得られる. $∠ B D A = ∠ M C A$ より, $△ A B D ∽ △ A M C$ となる.したがって, $A P$ はSymmedianである.

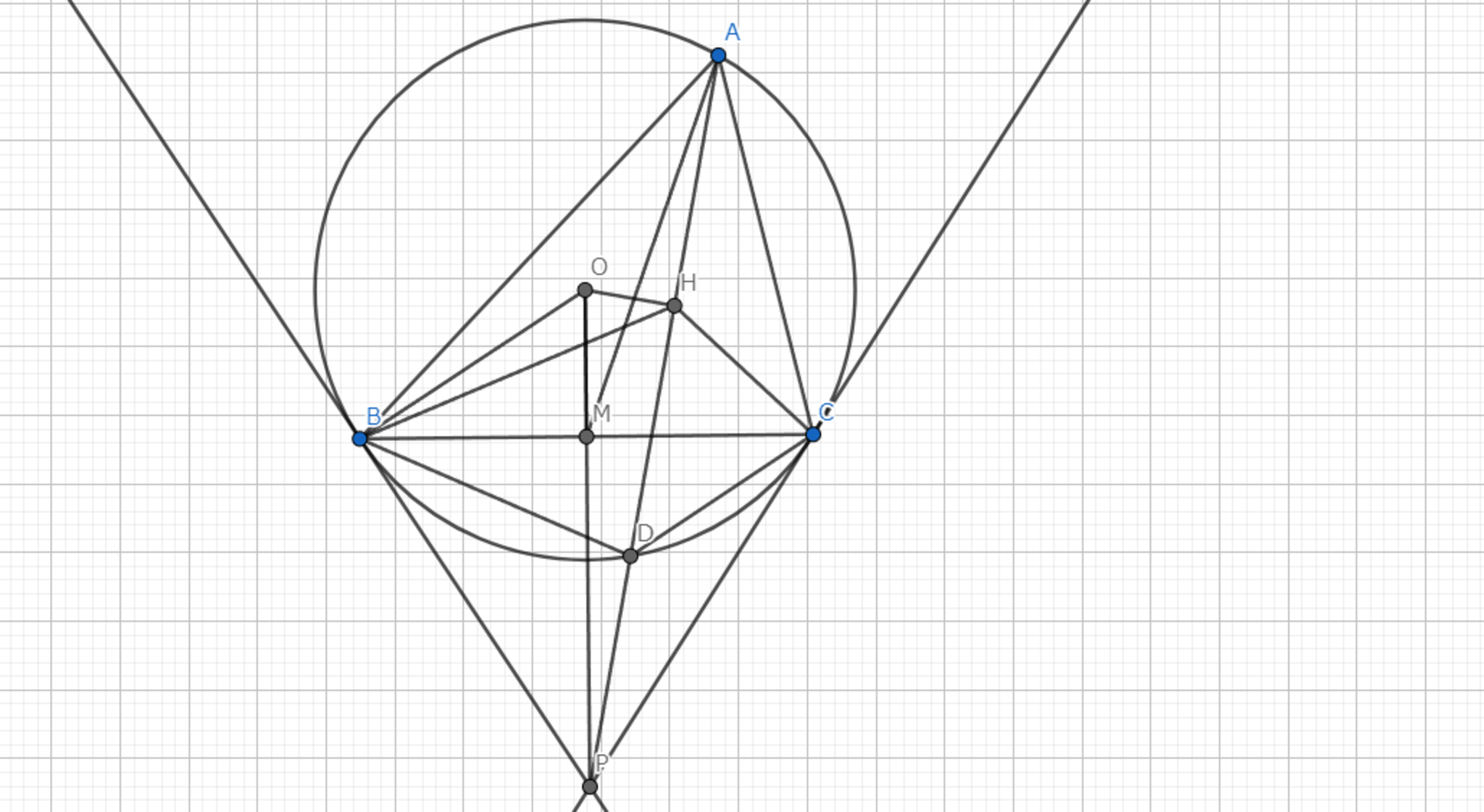Symmedian-作図2

折角なので,もうひとつ代表的なSymmedianの作図方法を見ていきましょう.

Symmedianの作図2

三角形 $A B C$ の外接円の $A$ における接線と直線 $B C$ との交点を $K$ とする. $K$ から三角形
$A B C$ の外接円へ引いた接線との接点を $D$ とすると, $A D$ はSymmedianである.

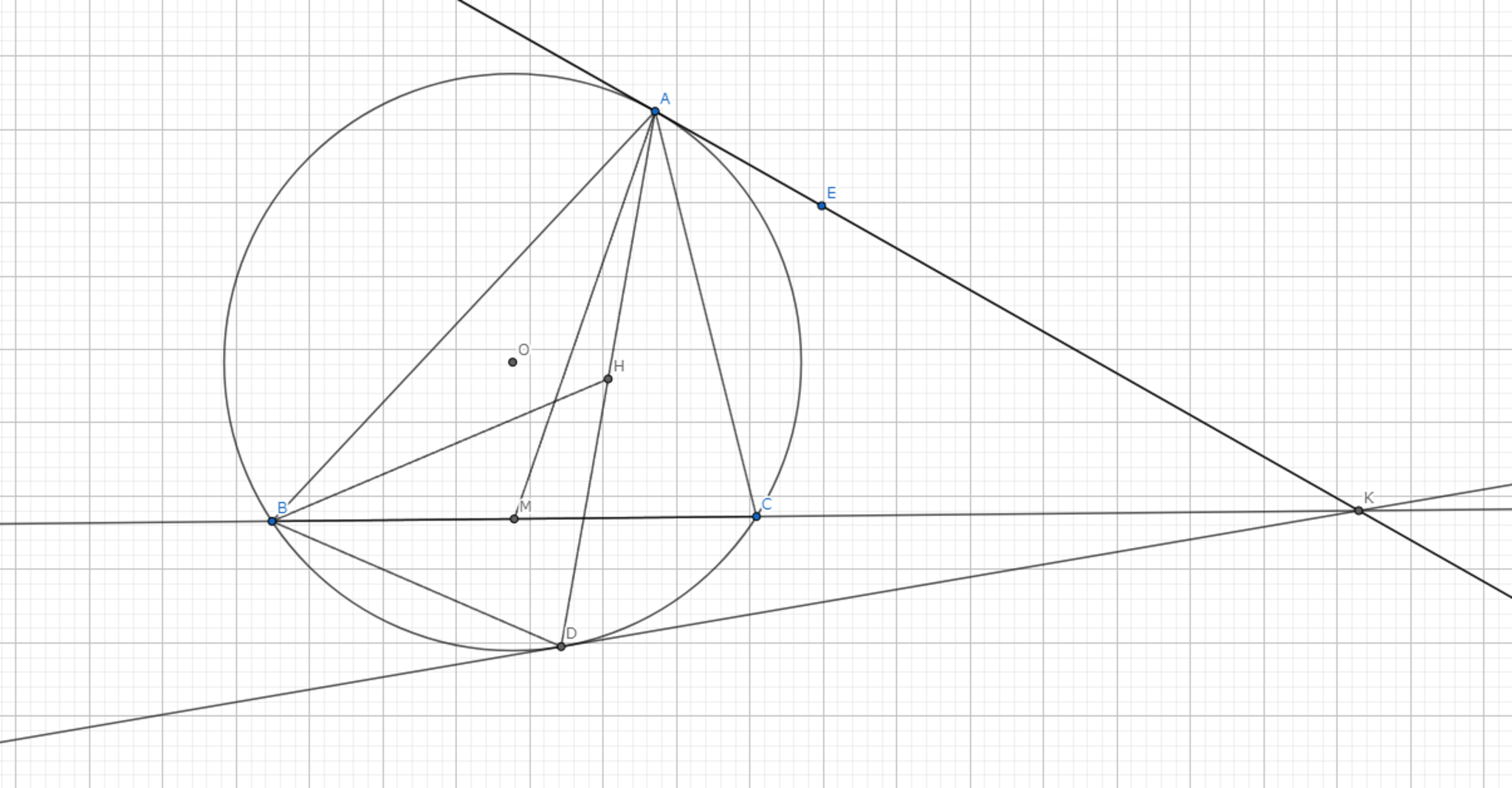
Symmedian-作図3

こちらも同様にSymmedianが作図できていることを確認していきましょう.

方針:定理1と同様の手法を用いる.

定理1より, $B K$ は三角形 $B D A$ のSymmedianである.したがって, $∠ A B C = ∠ H B D$ である.また,円周角の定理より, $∠ B C A = ∠ B D H$ である.よって $△ A B D ∽ △ A M C$ が従う. $| B D | : | D H | = | B C | : | C A |$ が得られる.また, $M, H$ が中点であることより,定理1の証明と同様に $△ A B C ∽ △ H B D$ である.したがって, $A D$ はSymmedianである.

Symmedian-作図4

ちなみに,定理1を用いない証明も存在します.

Symmedianの基本性質

上の証明の途中でいくつか面白い性質が出てきましたね.いったんそれらをまとめていきたいと思います.

Symmedianの性質1

図において, $A D$ はSymmedianである.このとき,以下の性質が成り立つ.
・ $A D$ , $B, C$ の接線は共点である.
・ $∠ B H D = ∠ C H D$ である.(角の二等分線)
・ $A D$ の中点 $H$ と $B, P, C, O$ の5点は同一円周上にある.
・ $B C$ は三角形 $A C D$ (三角形 $A B D$ )のSymmedianである.

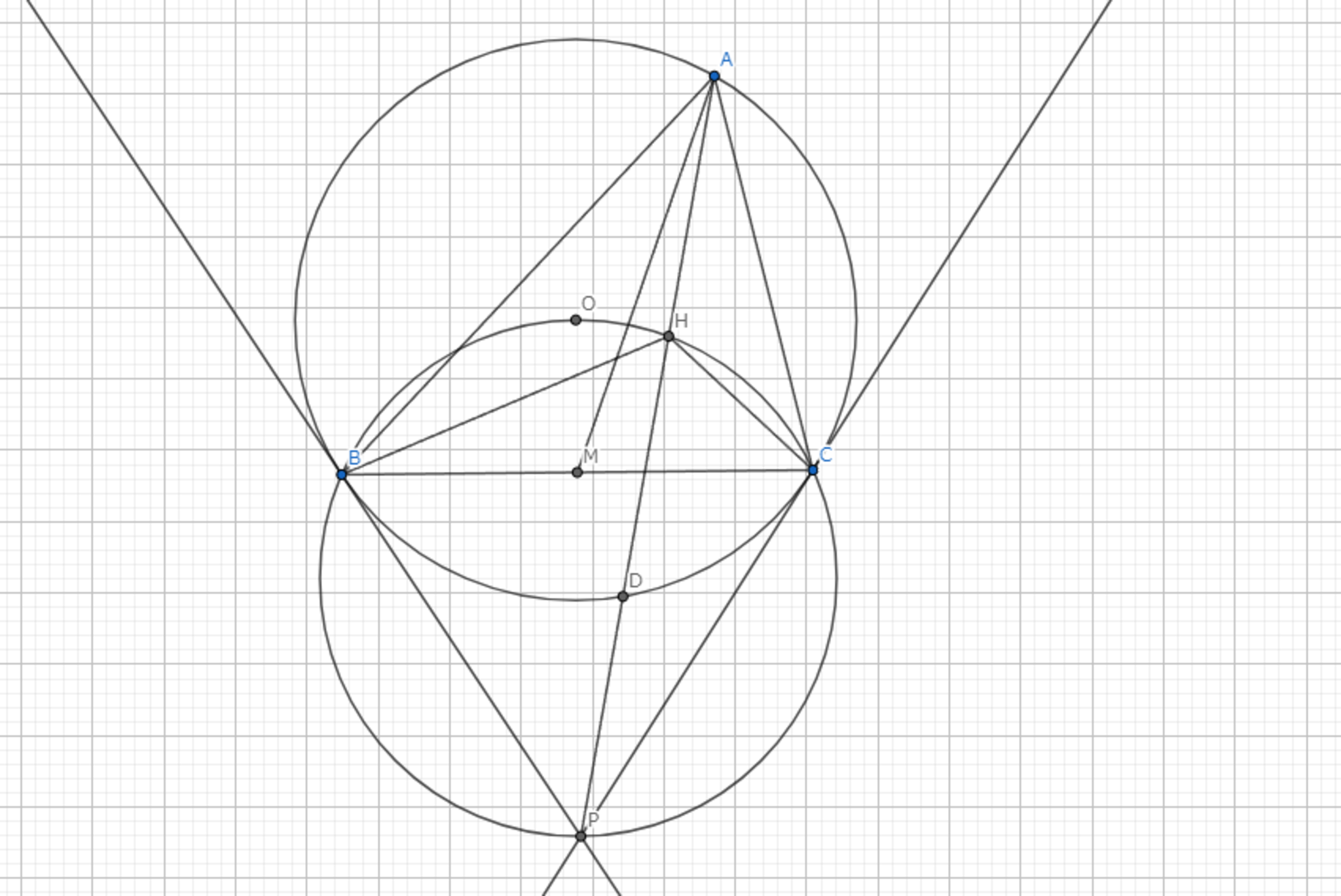Symmedian-性質1

ここでは, $A D$ がSymmedianの時にこれらの性質が成り立つことを改めて示してみましょう.

$A D$ はSymmedianなので, $∠ B A D = ∠ C A M$ である.また,円周角の定理より, $∠ A B C = ∠ A D C$ である.したがって, $△ A B M ∽ △ A D C$ である.よって, $| A D | : | D C | = | A B | : | B M |$ である.また, $M, H$ は中点であるから $| H D | : | D C | = | A B | : | B C |$ が得られる.このことから, $△ A B C ∽ △ H D C$ 従う. $∠ D H C = ∠ B A C = ∠ C O M = ∠ C O P$ が得られる.よって,5点 $O, H, C, P, B$ は共円である.(3つ目の性質)

また,5点が共円であるから簡単な角度計算より, $∠ B H P = ∠ C H P$ である.(2つ目の性質)
さらに,三角形 $H B C$ において, $H P$ は角の二等分線であるから有名事実より, $H P$ は $\overset{⌢}{B C}$ のうち $O$ を含まないほうの中点を通るから $A D$ は $P$ を通る.(1つ目の性質)

4つ目の性質は定理1と定理2を用いることで容易に得られる.

もう少し,Symmedianの性質を見ていきましょう.

$A D$ はSymmedianである.このとき, $A D$ 上に点 $G$ を取ると $| G H | : | G I | = | A B | : | A C |$

$A D$ はSymmedianであるから $△ A G I ∽ △ A M E$ , $△ A G H ∽ △ A M F$ である.よって, $| G H | : | G I | = | M F | : | M E |$ が得られる. $M$ は中点なので $△ A B M = △ A C M$ .したがって, $| A B | \cdot | E M | = | A C | \cdot | F M | ⟺ | M F | : | M E | = | A B | : | A C |$ である.

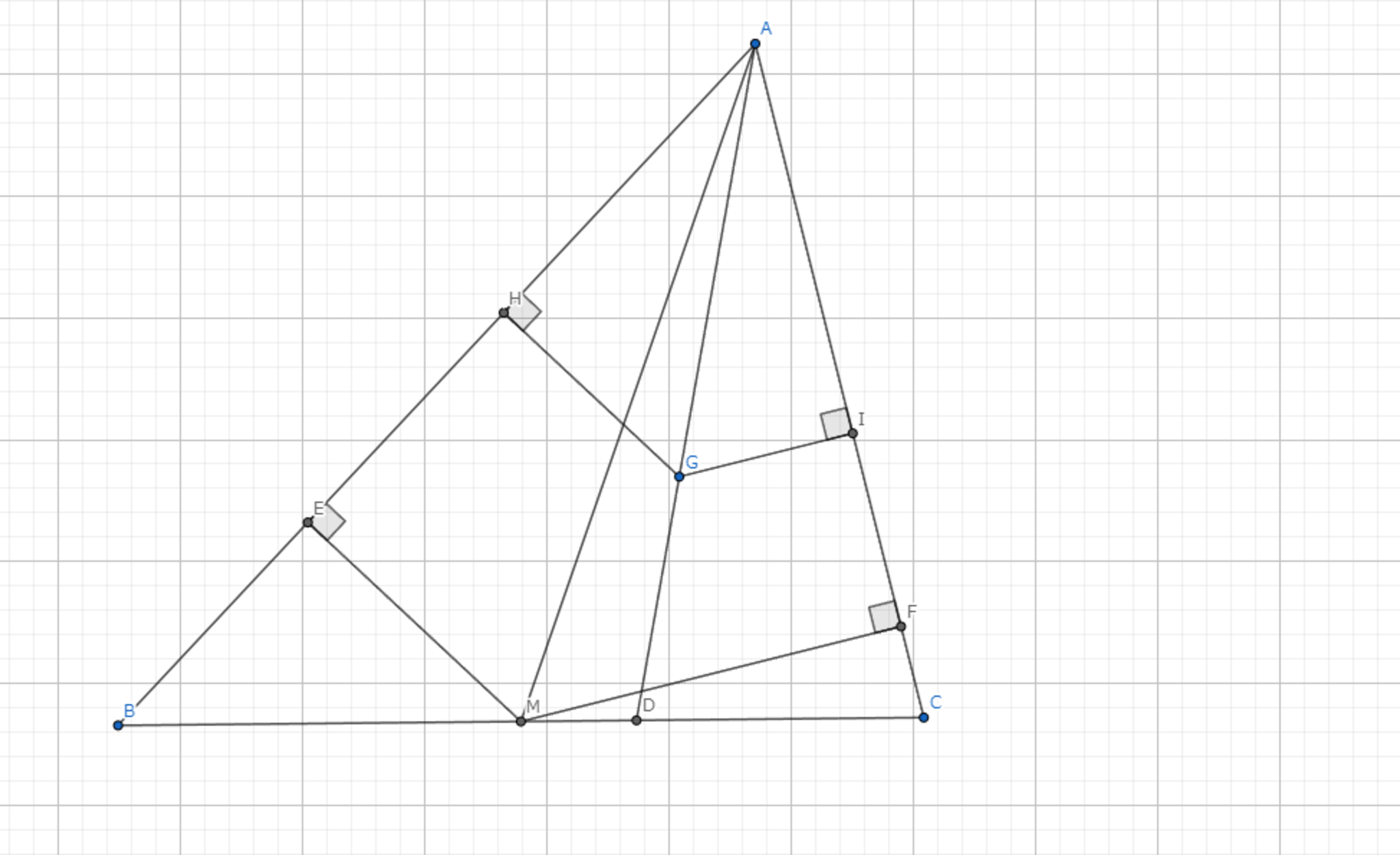lemma-1 lemma-1

補題を示したのは下記の有名な定理のためです.

Symmedianの性質2/Steiner's Ratio Theorem

図において, $A D$ をSymmedianとすると, $| B D | : | C D | = | A B |^{2} : | A C |^{2}$ が成り立つ.

$| B D | : | C D | = △ A B D : △ A C D = | A B | \cdot | D F | : | A C | \cdot | D E |$ .ここで,補題4より, $| D F | : | D E | = | A B | : | A C |$ である.したがって, $| B D | : | C D | = | A B |^{2} : | A C |^{2}$ .

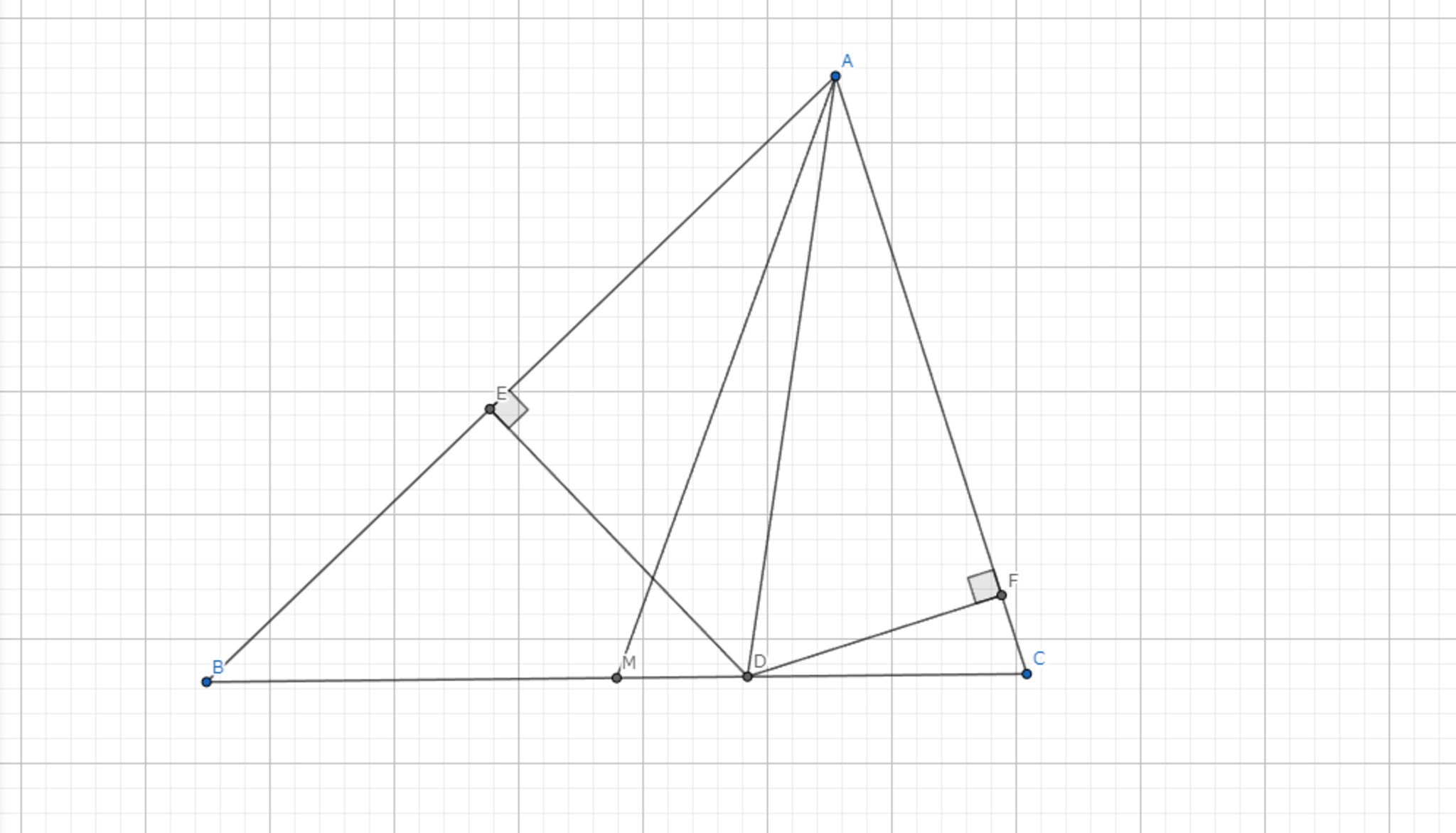Steiner's Ratio Theorem-2

Symmedianの性質3/antiparallel

Symmedianは逆平行線の中線である.

逆平行とは簡単に言うと, $∠ A B C = ∠ A F E$ となるような状況のことを言います.

$B C$ と $E F$ は逆平行なので $∠ A B C = ∠ A F E$ , $∠ A C B = ∠ A E F$ である.したがって, $△ A B C ∽ △ A F E$ である.また, $A D$ がSymmedianなので $∠ E A N = ∠ C A M$ であるから $△ A C M ∽ △ A E N$ である. $| B C | : | M C | = | F E | : | N E | = 2 : 1$ であるから $N$ は $F E$ の中点である.

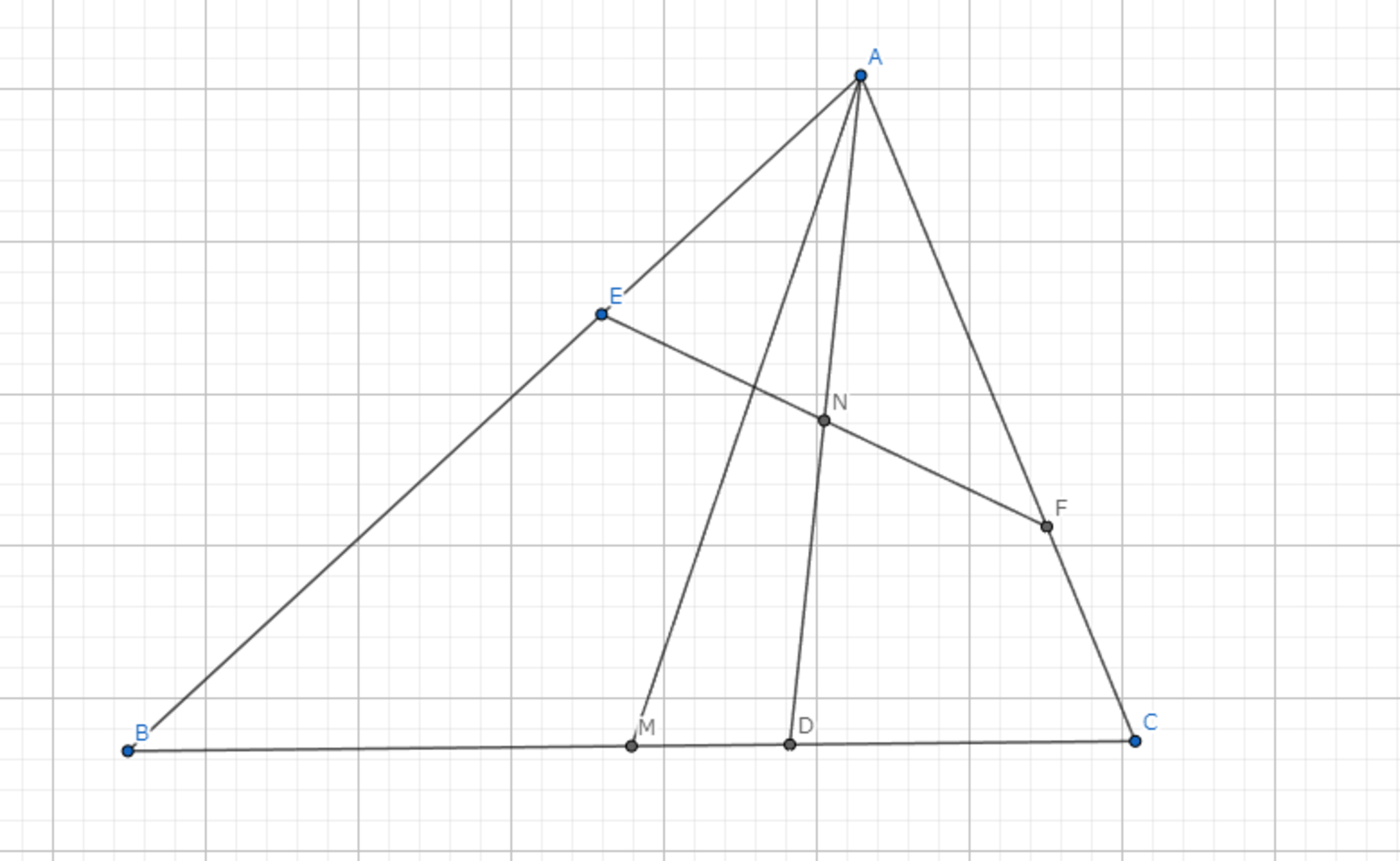Antiparallel-1

ここまでいろいろな面白い性質を紹介してきましたがSymmedianの性質は数えきれないほど存在します.あくまでもこれらは"基本"性質です.

類似重心(ルモアーヌ点)

一つの三角形に対して三つのSymmedianが存在しますがそれらは一点で交わるのでしょうか？実際に図を描いてみると交わりそうですね.

類似重心

三角形の三本のSymmedianは一点で交わる.これを類似重心と呼ぶ.

方針:チェバの定理の逆より $\frac{| A F |}{| F B |} \cdot \frac{| B D |}{| D C |} \cdot \frac{| C E |}{| E A |} = 1$ を示す.

ここで,Steiner's Ratio Theoremより $| A F | : | F B | = | C A |^{2} : | B C |^{2} ⟺ \frac{| A F |}{| F B |} = \frac{{| B C |}^{2}}{{| C A |}^{2}}$ である.他の項に対しても同様の変形をすると, $\frac{| A F |}{| F B |} \cdot \frac{| B D |}{| D C |} \cdot \frac{| C E |}{| E A |} = \frac{{| B C |}^{2}}{{| C A |}^{2}} \cdot \frac{{| C A |}^{2}}{{| A B |}^{2}} \cdot \frac{{| A B |}^{2}}{{| B C |}^{2}} = 1$ となって,3本のSymmedianは一点で交わることが示された.

類似重心-1

この一点は類似重心やルモアーヌ点と呼ばれています.ルモアーヌ点の性質もたくさん存在しますが,今回は少しだけ面白い性質を紹介しておきます.

類似重心 $G^{'}$ から $B C, C A, A B$ へ下ろした垂線の長さを $x, y, z$ とすると, $x : y : z = | B C | : | C A | : | A B |$ が成り立つ.

これは補題4が刺さりそうですね.

$G^{'}$ は3つのSymmedian上の点であるので、補題4より, $x : y = | B C | : | C A |$ , $y : z = | C A | : | A B |$ , $z : x = | A B | : | B C |$ である.よって, $x : y : z = | B C | : | C A | : | A B |$

三角形 $A B C$ の内部の点 $P$ から $A B, B C, C A$ へ下ろした垂線の長さを $z, x, y$ とすると, $x^{2} + y^{2} + z^{2}$ が最小となるような $P$ は類似重心である.

$| A B | = c, | B C | = a, | C A | = b$ とする.コーシーシュワルツの不等式より, $(a^{2} + b^{2} + c^{2}) (x^{2} + y^{2} + z^{2}) \geq (a x + b y + c z)^{2}$ が成り立つ.

$(x^{2} + y^{2} + z^{2}) \geq \frac{{(a x + b y + c z)}^{2}}{(a^{2} + b^{2} + c^{2})} ⟺ (x^{2} + y^{2} + z^{2}) \geq \frac{4 S^{2}}{(a^{2} + b^{2} + c^{2})}$
ここでの統合成立条件は $a : b : c = x : y : z$ でありそのような点は類似重心である.

Symmedianの作図(応用編)

Symmedianの作図をもう少し深掘りしてみましょう.

直角三角形におけるSymmedian

直角三角形におけるSymmedianは対辺への垂線であることを示せ.

2本の接線は必ずしも一点で交わるとは限りません.そのようなケースを考えてみましょう.

$∠ B A D = ∠ C A M$ であり, $∠ C A M = ∠ A C M$ である. $∠ A M C = 180 ° - 2 ∠ M A C$ であり,円周角の定理より, $∠ A B D = 90 ° ∠ M A C$ より, $∠ A D M = 90 °$ となる.従って,Symmedianは垂線である.

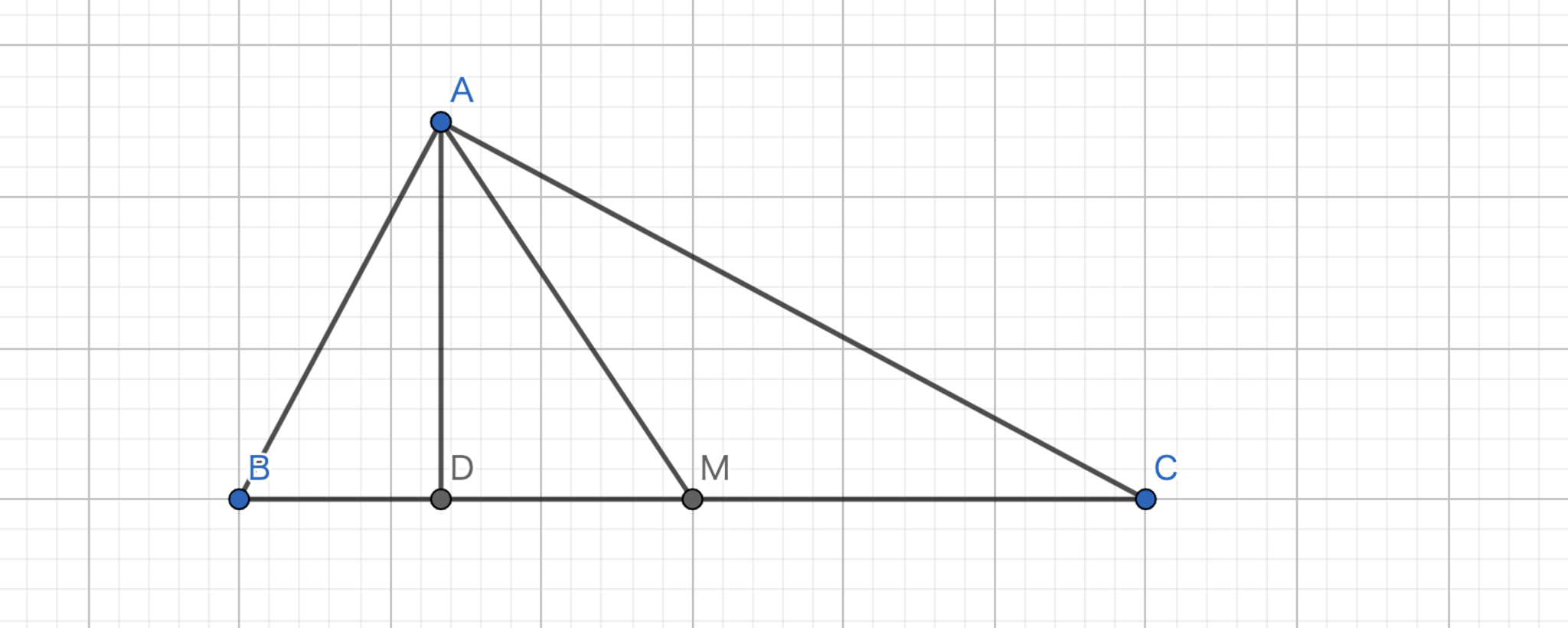直角三角形におけるSymmedian

このことから,外接円の接線とSymmedianは一点で交わるか平行になるかの二択であるとわかりましたね.これは根心と似ていますね.

Symmedianの作図-応用編1

三角形 $A B C$ において図のように $A B$ , $A C$ を一辺とする正方形を考える.この時,三角形 $A D G$ の外心と $A$ を結んだ直線はSymmedianとなることを示せ.

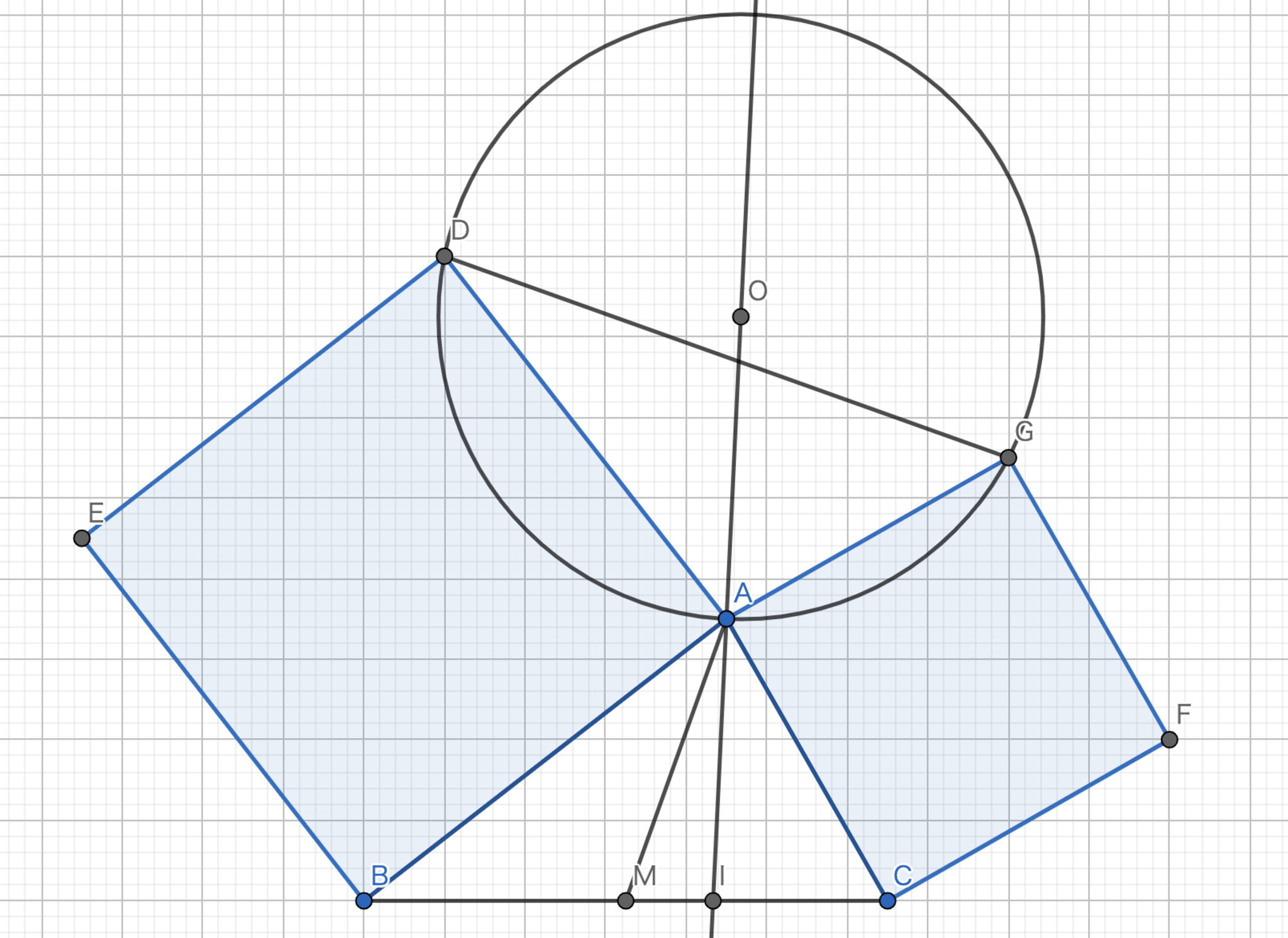Symmedian-作図応用編1-1

$\frac{1}{2} ∠ B A C + 90 ° + \frac{1}{2} ∠ D A G = 180 °$ より, $∠ B A C$ の角の二等分線と $∠ D A G$ の角の二等分線は一致する.一方で,三角形 $D A G$ に注目すると,直線 $I A$ は外心を通る.外心と垂心は等角共役関係にあることから直線 $M A$ が垂心を通ることを示す.すなわち,直線 $M A$ が $D G$ と直行することを示ば良い. $A$ を中心として三角形 $D A G$ を $270 °$ 回転した三角形 $H A C$ を考える.中点連結定理より, $A M / / H C$ である.従って,直線 $M A$ は $D G$ と直行する.これより, $A I$ はSymmedianである.

Symmedian-作図応用編1-2

Symmedian-作図応用編2

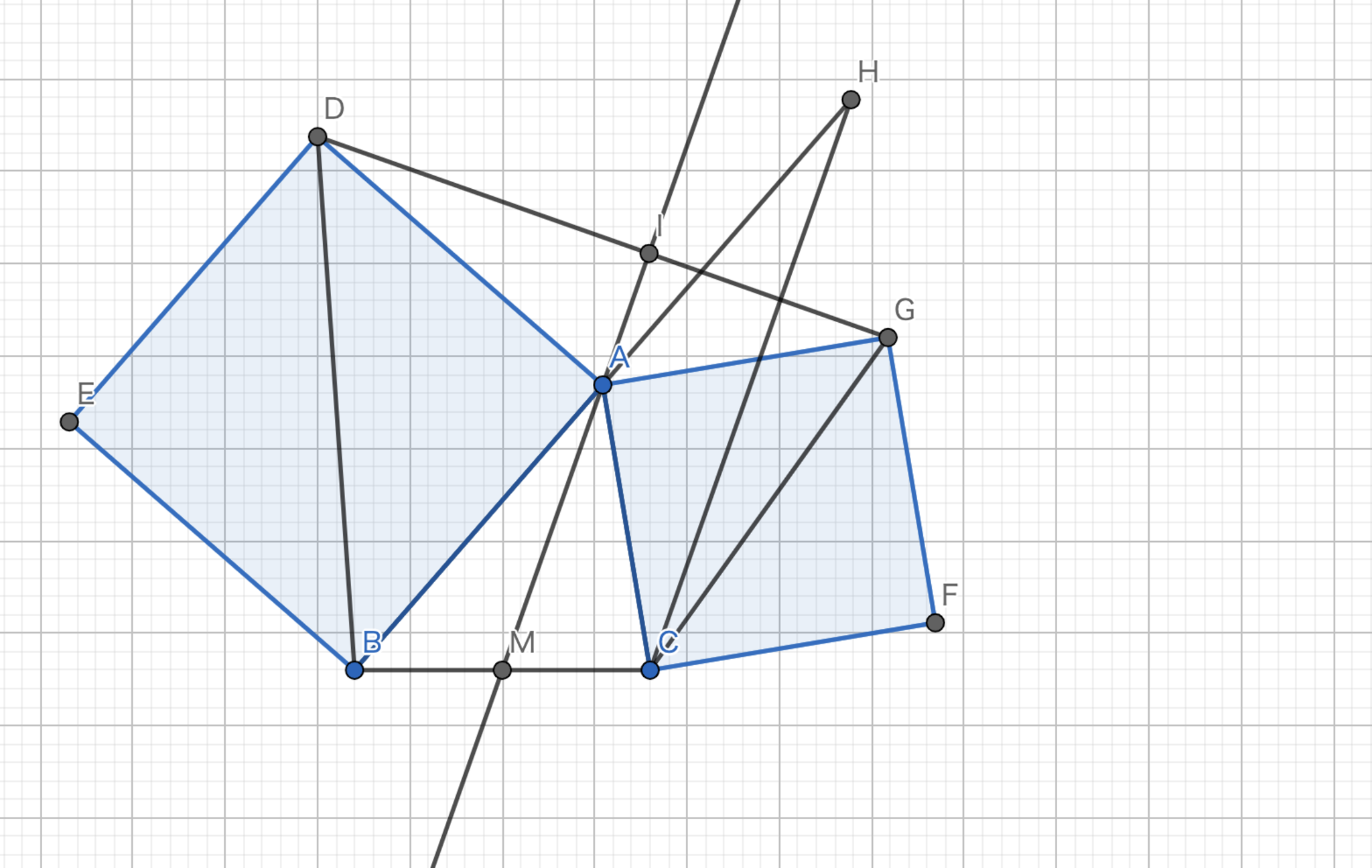
三角形 $A B C$ において,辺 $A B, A C$ 上に $B C / / D E$ となるように点 $D, E$ をとる. $B E$ と $C D$ の交点を $F$ とする.三角形 $B D F, C E F$ の外接円の交点のうち $F$ でないものを $G$ とすると, $A G$ はSymmedianであることを示せ.

Symmedian-作図応用編2-1

とても自然な流れでSymmedianが登場しましたね...!

方針:補題4を使う

簡単なangle-chaseより, $△ D B G ∽ △ C E G$ である. $H_{B D}, H_{C E}$ を $G$ から $B D, C E$ へと下ろした垂線の長さとする.ここで,補題4より, $H_{B D} : H_{C E} = | A B | : | A C |$ を示せば良い.

$| A B | : | A C | = | B D | : | C E | = △ D B G : △ C E G = H_{B D} : H_{C E}$ であるから題意は示された.

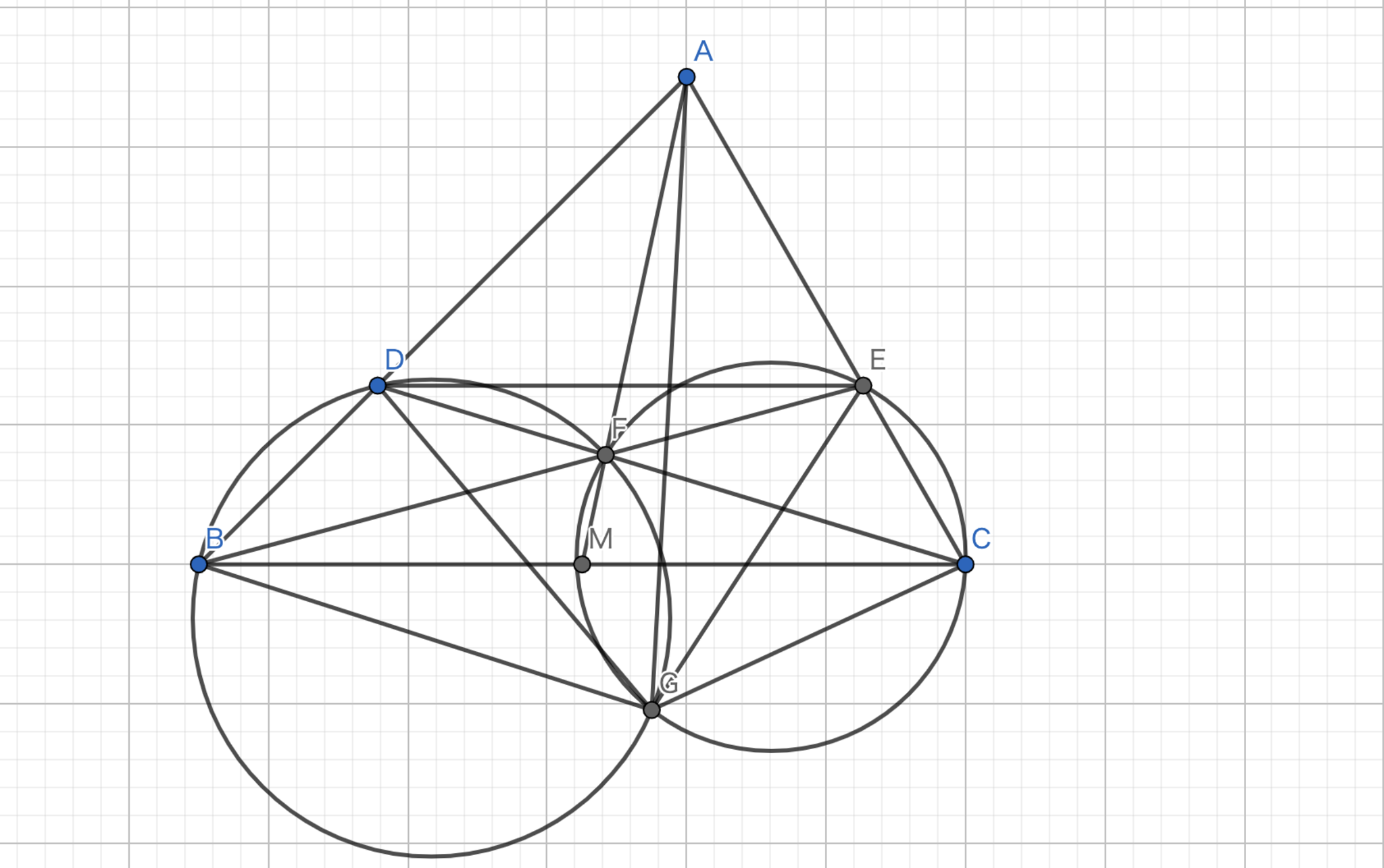Symmedian-作図応用編2-2

Symmedian-作図応用編3

三角形 $A B C$ において,辺 $A B, A C$ 上に $B C / / D E$ となるように点 $D, E$ をとる.三角形 $B E A, C D A$ の外接円の交点のうち $A$ でないものを $F$ とすると, $A F$ はSymmedianであることを示せ.

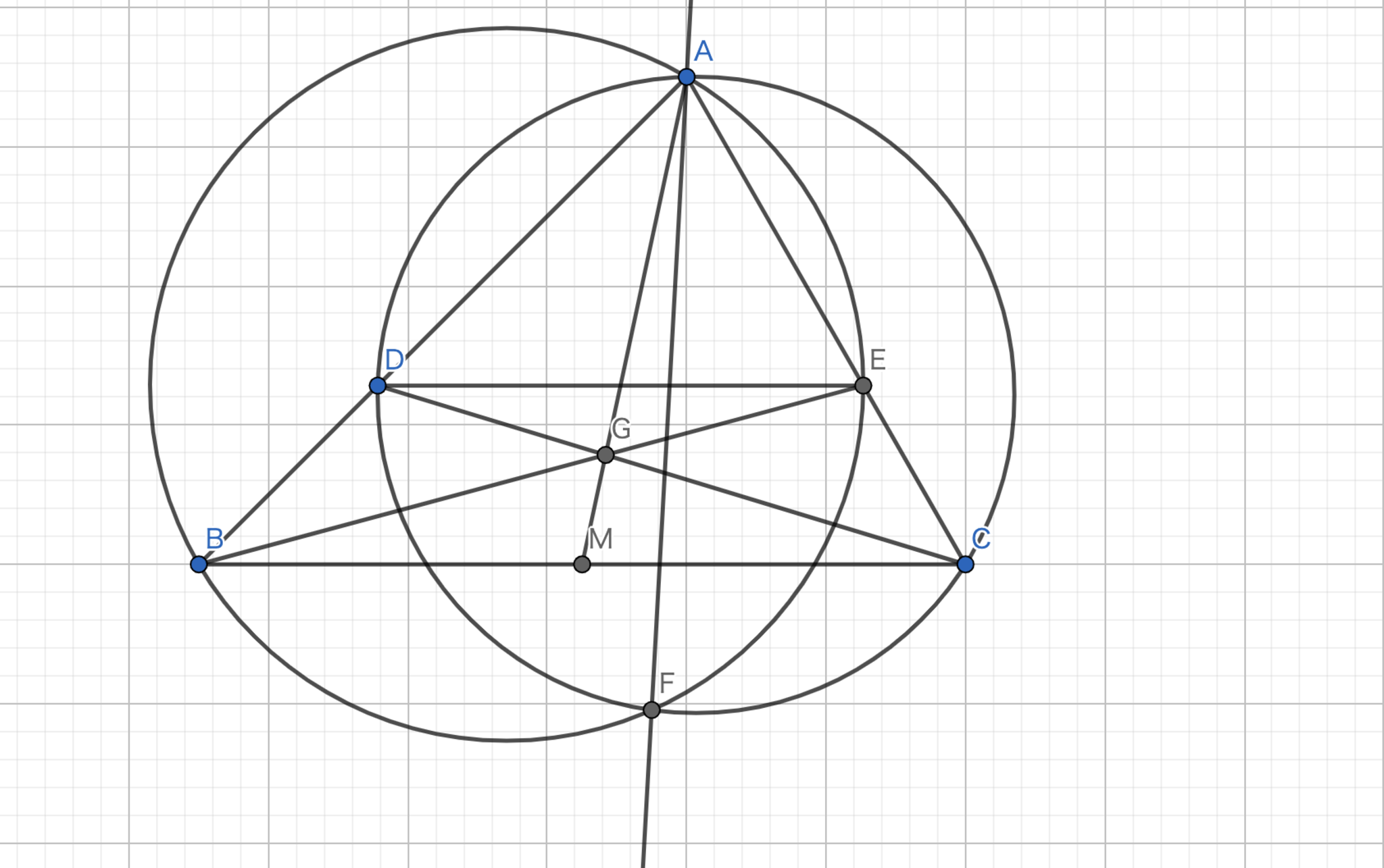Symmedian-作図応用編3-1

方針:問題3を用いる

$∠ D B F = ∠ F E C$ , $∠ B D P = ∠ E C F$ であるから $△ D B F ∽ △ C E F$ より $△ B F E ∽ △ D F C$ が従う.よって,4点 $B, D, G, F$ と $C, E, G, F$ はそれぞれ共円である.ここで,問題3より $A F$ はSymmedianである.

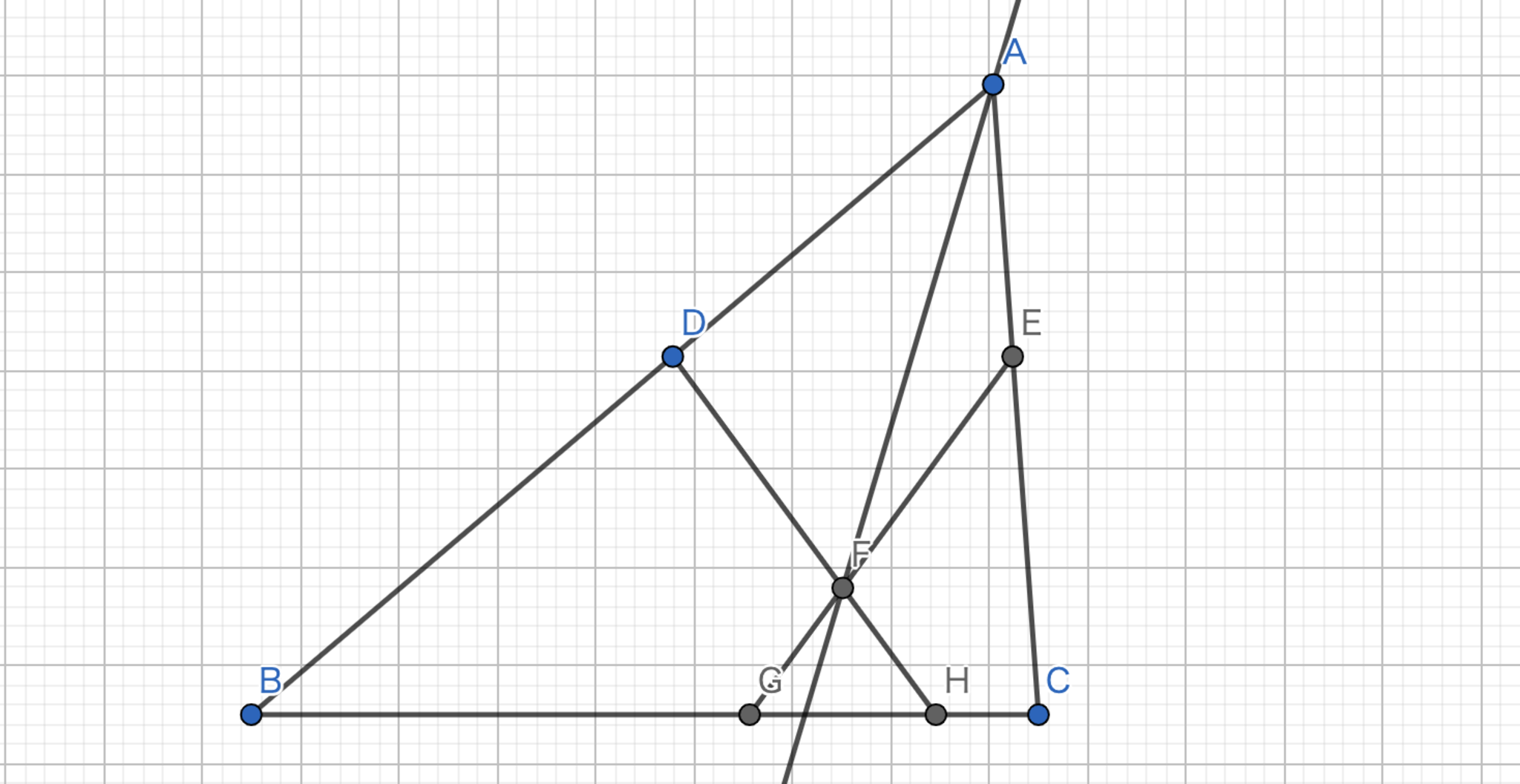
Symmedian-作図応用編3-2

三角形 $A B C$ において辺 $A B, A C$ 上に点 $D, E$ を $B C / / D E$ となるようにとる. $D$ を通り $A C$ に逆平行な直線と $E$ を通り $A B$ に逆平行な直線の交点を $P$ としたとき, $A F$ はSymmedianであることを示せ.

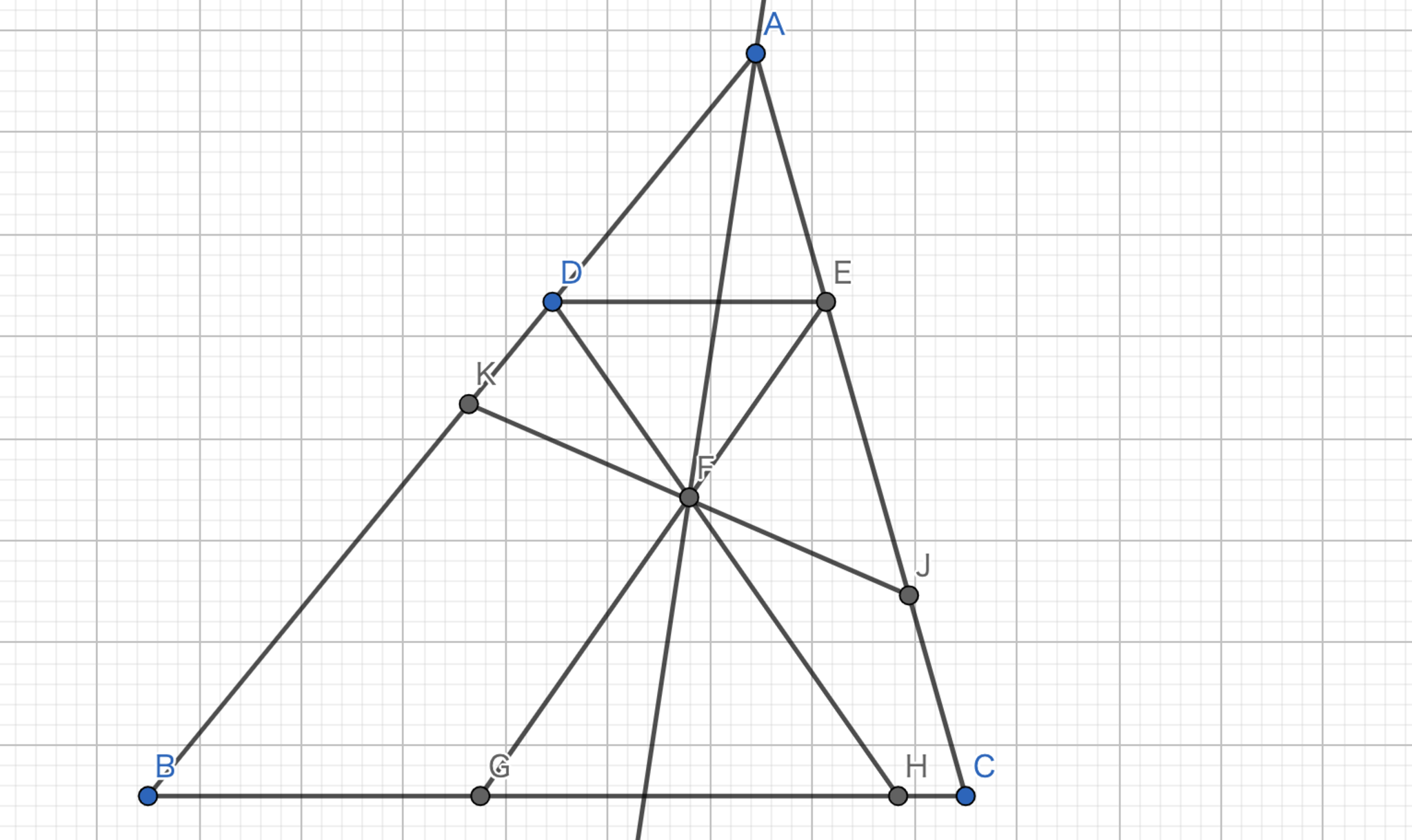
Symmedian-作図応用編4-1

残りの逆平行線を引いてそこの中点を通ることを示していきましょう.

$∠ B A C = A, ∠ C B A = B, ∠ A C B = C$ とする. $D H, E G$ は逆平行線であるから, $∠ B D C = C, ∠ C E G = B$ である. $A + B + C = 180 °$ であるから, $∠ D H G = ∠ E G H = A$ である.また, $D E / / G H$ なので $∠ F D E = ∠ F E D = A$ である.従って, $| F D | = | F E |$ である.ここで, $E$ を通り $B C$ と逆平行な補助線を引く.すると, $∠ K D F = ∠ D K F = C$ であり, $| F K | = | F D |$ である.同様に, $| F J | = | F E |$ である.従って, $E$ は $K J$ の中点である.従って,定理6より $A F$ はSymmedianである.

Symmedian-作図応用編4-2

@I_______nu

三角形ABCの外接円をΩとして,2点B,Cについてのアポロニウスの円であってAを通るようなものをωとする.この時,以下の性質が成り立つ.

・ $ω$ を $Ω$ で反転させても不変である.
・ $ω$ の中心, $A$ , $B C$ の中点を通る円を $Ω$ で反転させるとSymmedianとなる.

僕は反転を初等的に扱った経験があまりないので紹介だけです.申し訳ありません.

調和四角形

Vietnam TST

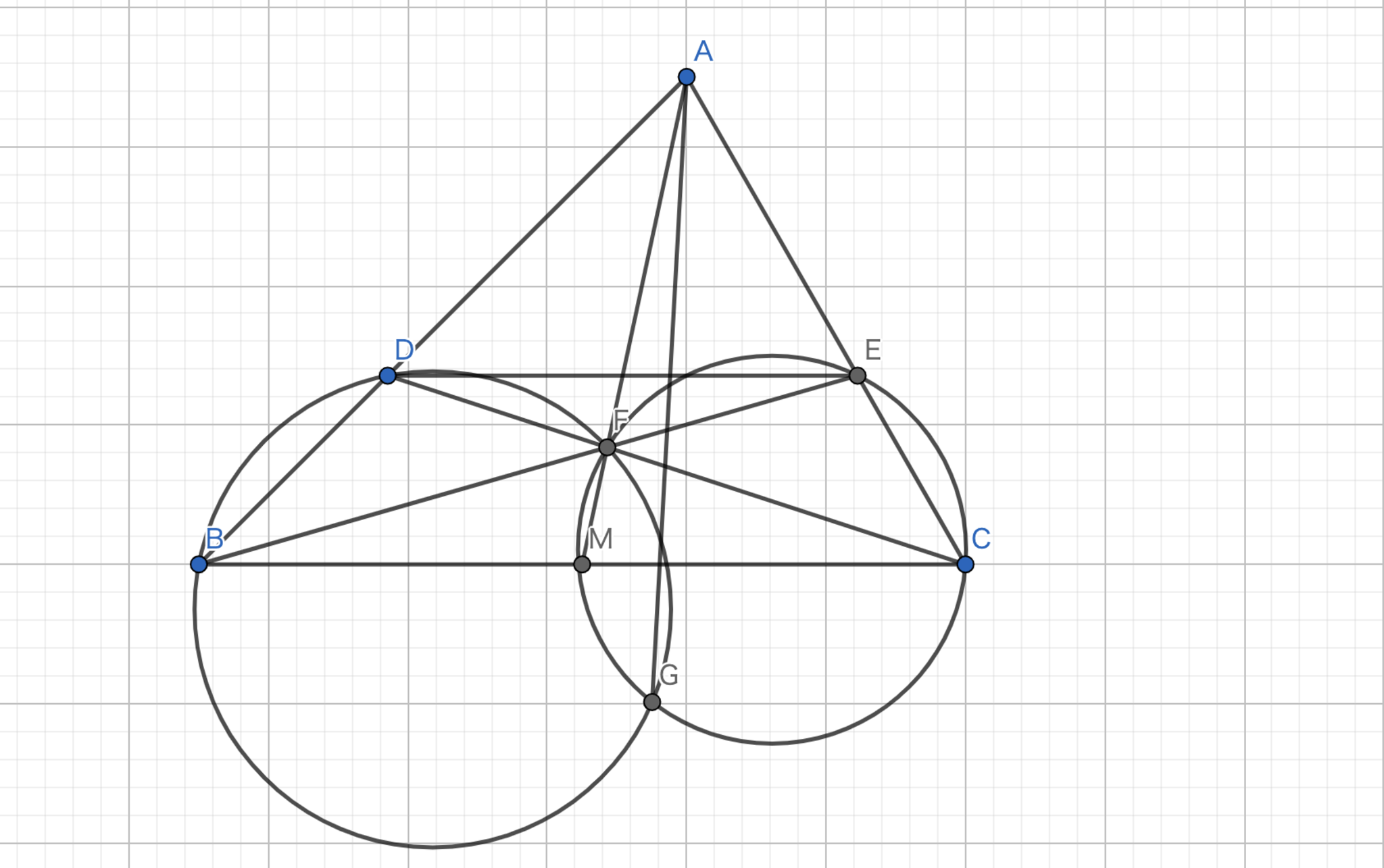
三角形 $A B C$ の外接円を $Ω$ として, $M$ を $B C$ の中点とする.円 $I_{1}$ を $B, M$ を通り, $A B$ と接する円とする.円 $I_{2}$ を $C, M$ を通り, $A C$ と接する円とする.この時,円 $Ω, I_{1}, I_{2}$ が一点で交わることを示せ.

$I_{1}$ と $I_{2}$ の交点 $X$ が $A B C$ の外接円上に存在することを示す.接弦定理より, $∠ A B C = ∠ B X M, ∠ A C B = ∠ C X M$ である. $∠ B A C + ∠ B X C = 180 °$ より四点 $A B X C$ は共円である.

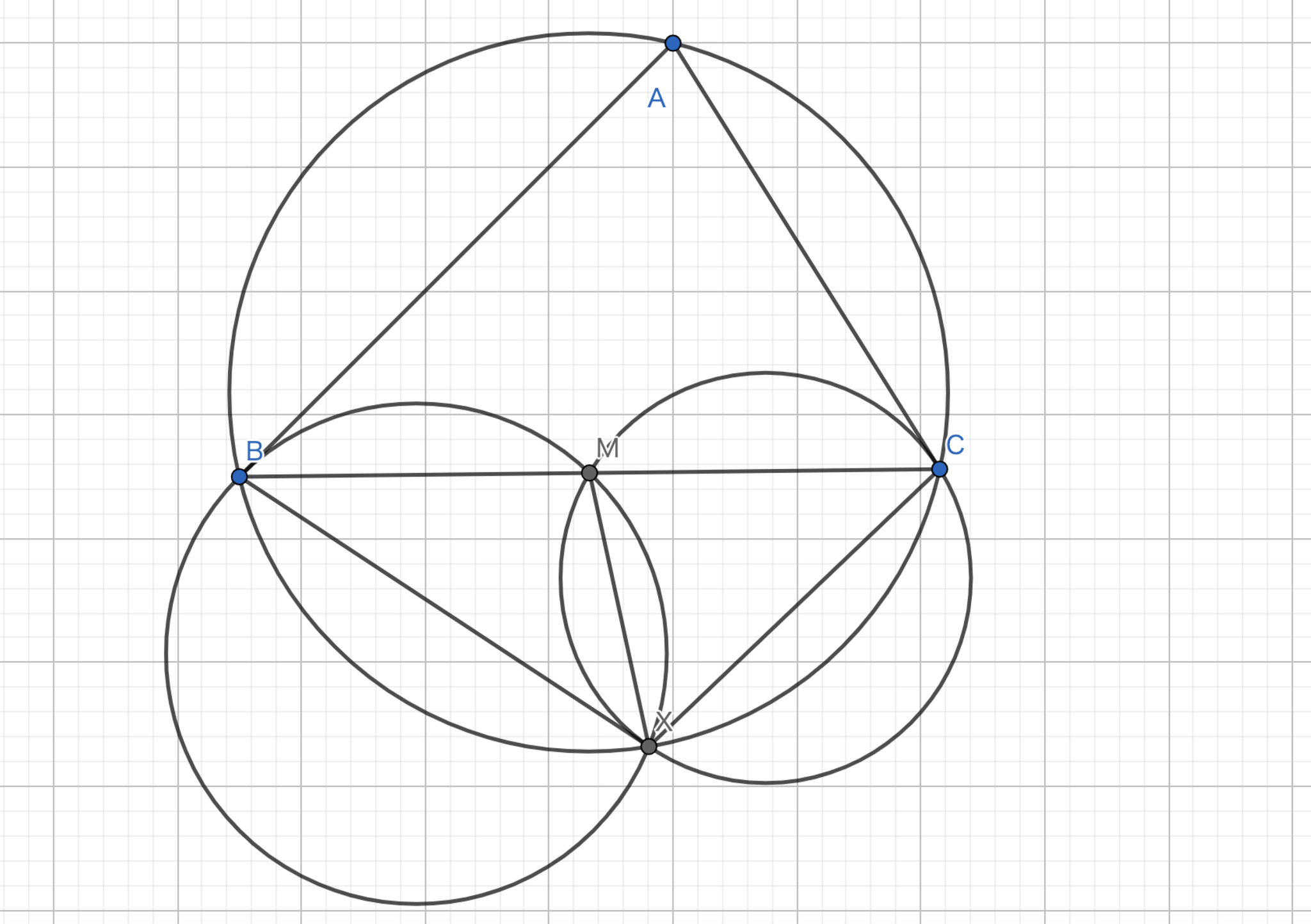調和四角形-1

さて,問題自体はこれで終わっても良いですがせっかくなのでSymmedianとの関係性も見ていきましょう.これはイメージ的には問題4の特殊な場合と考えれば良いですね.

Symmedianの確認

簡単なangle-chaseより $∠ C D M = ∠ B D A$ であるから $D A$ は三角形 $D B C$ の $D$ に関するSymmedianである.ここで $A$ から $B D, C D$ はと下ろした垂線の長さを $d_{1}, d_{2}$ とすると,補題4より以下が成り立つ. $d_{1} : d_{2} = | A B | : | A C | = | D B | : | C D |$ である.ここで, $D$ について注目すると,補題4より $A D$ は三角形 $A B C$ に関してのSymmedianである.

調和四角形-2

ちなみに,このような四角形は調和四角形と呼びます.ここで,調和四角形に関しての性質をいくつか見ていきましょう.

調和四角形

四角形 $A B C D$ が円に内接して, $| A B | \cdot | C D | = | B C | \cdot | D A |$ を満たすとき調和四角形と呼ぶ.

調和四角形には以下の同値な言い換えが存在します.

調和四角形 $A B C D$ において $A C$ は三角形 $A B D$ の $A$ におけるSymmedianである.

まぁ,補題4より明らかですね.これはもちろん三角形 $A B C$ などにも成り立ちます.

複比と調和点列

実践問題は難しい問題も含まれています.一旦ここでは事前準備として複比と調和点列について扱っていきます.あくまでもSymmedianについての記事なのでここでは軽くしか扱いませんので各自で調べることを推奨します.知っている人は飛ばしてもらって構いません.

複比

四点 $A, P, B, Q$ に対して $\frac{A P}{B P} \times \frac{B Q}{A Q}$ を複比といい, $(A, B; P, Q)$ と表す.

イメージとしては「比と比の掛け算」です.

一点 $O$ を通る4つの直線と二つの直線がなす複比は等しい.

簡単なので証明は省略します.

調和点列

$(A, B; P, Q) = 1$ となるような点列を調和点列という.

調和点列には同値な言い換えがいくつか存在しますが代表的なものを紹介しておきます.

四点 $A, P, B, Q$ が調和点列ならば $| A M | \cdot | A B | = | A P | \cdot | A Q |$ である.ただし, $M$ は $P Q$ の中点である.

こちらも簡単なので証明は省略します.

実践問題

ここからは実践的な問題を通じてSymmedianの性質をさらに深掘りして行きたいと思います.Symmedianは何が嬉しい？という疑問も解決できるのではないかと思います.とりあえず簡単な問題から考えていきましょう.

Brilliant

三角形 $A B C$ は $O$ を中心とする円 $Ω$ に内接している. $B C$ の中点を $M$ とする.　 $Ω$ に関する $B, C$ においての接線の交点を $P$ とする. $A P$ と $Ω$ の交点のうち $A$ でないものを $D$ とする. $∠ B D M = 27 °$ であったとき, $∠ A O C$ を求めよ.

四角形 $A B D C$ は調和四角形である.従って, $A D$ は三角形 $D B C$ における $D$ のSymmedianである.従って $∠ B D M = ∠ C D A = 27 °$ である.さらに円周角の定理より, $∠ C D A = ∠ C B A = \frac{1}{2} ∠ A O C = 27 °$ 従って, $∠ A O C = 54 °$ である.

OMC087-A

円に内接する四角形 $A B C D$ は $| A B | \cdot | C D | = | B C | \cdot | D A |$ を満たします.線分 $B D$ の中点を $M$ とします. $| A B | = 127, | A D | = 129, | C M | = 32$ であるとき, $A M$ の長さを求めてください.

これは4eの水diffでした.

四角形 $A B C D$ は調和四角形である.従って, $A C$ はSymmedianである.直線 $A M$ と三角形 $A B C$ の外接円との交点のうち $A$ でない方を $C^{'}$ とする. $A C^{'}$ と $A C$ は等角共役線なので $∠ B A C^{'} = ∠ D A C$ である.円周角の定理より, $| B C^{'} | = | D C |$ .また, $| B M | = | D M |$ である. $∠ B A C = ∠ D A C^{'}$ であり,円周角の定理より, $∠ M D C = ∠ M B C^{'}$ である.従って, $△ B M C^{'} \equiv △ D M C$ である.このことから, $| C M | = | C^{'} M |$ が得られる.方べきの定理より, $| B M |^{2} = | A M | \cdot | M C^{'} | = | A M | \cdot | M C |$ である.さらに,中線定理より $| A B |^{2} + | A D |^{2} = 2 (| B M |^{2} + | A M |^{2})$ である.これらを併せて,以下の連立方程式を得る.

$\begin{array}{r} {\begin{cases} | B M |^{2} = 32 \cdot | A M | \\ 127^{2} + 129^{2} = 2 (| B M |^{2} + | A M |^{2}) \end{cases} \end{array}$

これを整理すると, $| A M |^{2} + 32 | A M | - (2^{14} + 1) = 0$ という二次方程式が出てきます. $2^{14} + 1$ の素因数分解に関してですが,これは $2^{1} 4 + 1 = 4 \cdot 8^{4} + 1^{4}$ とみることでソフィージェルマン恒等式より, $5 \times 29 \times 113$ とわかります.従って, $| A M | = 113$ です.Symmediaに気づくことで簡単に解ける問題でした.

実践問題2-1

@I_______nu

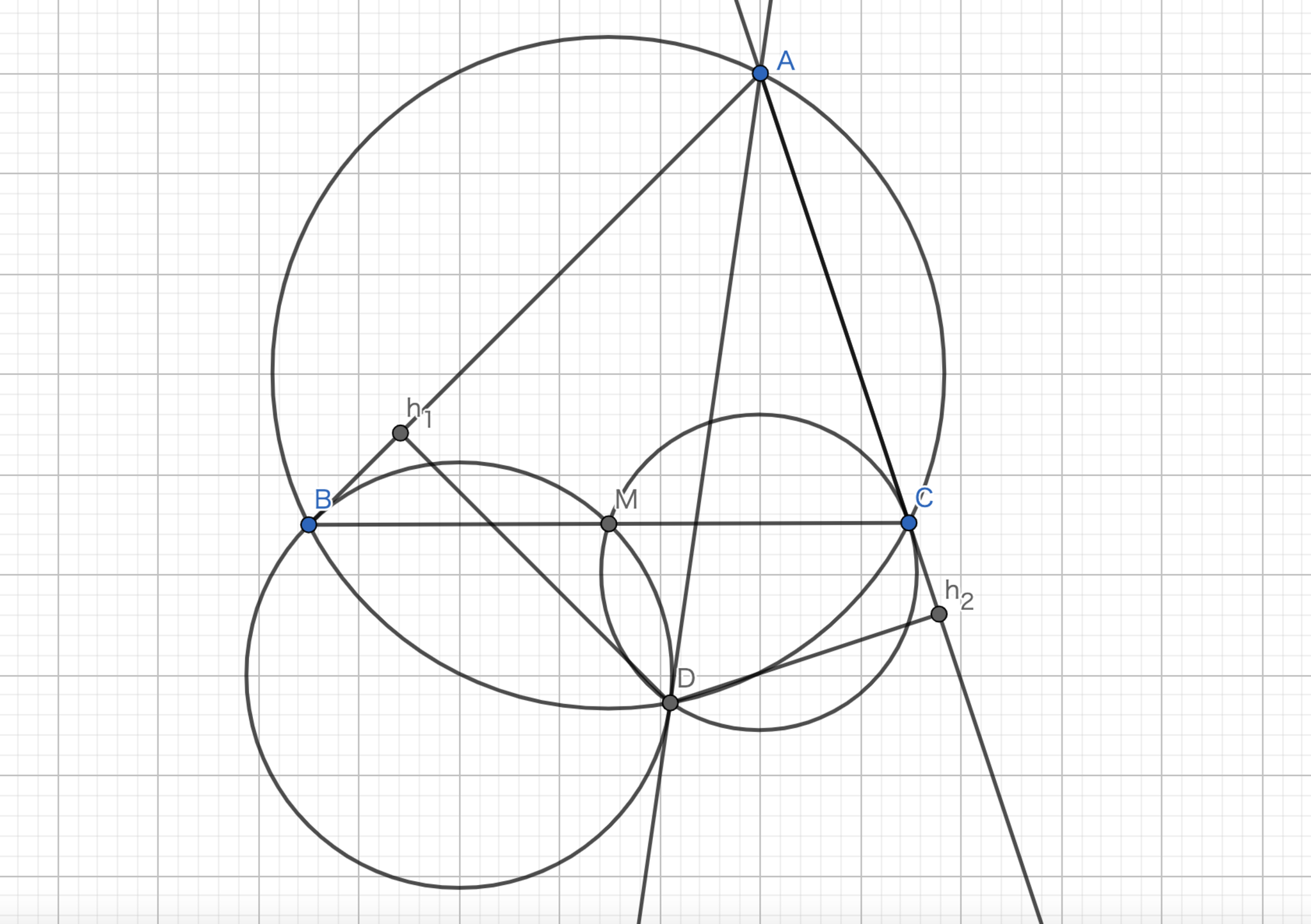
三角形 $A B C$ の垂心 $H$ から中線 $A M$ へと下ろした垂線の足を $P$ とする. $P$ を $B C$ に関して対称移動させた点を $A^{'}$ とすると, $A A^{'}$ はSymmedianとなることを示せ.

Symmedianの対称性に着目してみましょう.

$∠ H P M = ∠ H D M = 90 °$ より, $P, H, M, D$ は共円. $P H, M D$ の交点を $X$ とすると方べきの定理より, $| X H | \cdot | X P | = | X D | \cdot | X M |$ である.ここで, $B, D, C, X$ は調和点列なので $| X C | \cdot | X B | = | X D | \cdot | X M |$ である.従って,方べきの定理の逆より, $B, C, H, P$ は共円である.一方で有名事実として, $H$ を $B C$ に関して対称移動させた点は $H^{'}$ は三角形 $A B C$ の外接円上にくる.三点 $B C H$ で定まる円と $B C H^{'}$ で定まる円は対称だから $A^{'}$ は三角形 $A B C$ の外接円上にくる. $A M$ と三角形 $A B C$ の外接円の交点を $Y$ とすると, $Y$ は $M$ に関して $P$ と点対称なので $\overset{⌢}{B Y} = \overset{⌢}{P C}$ である.また, $A^{'}$ は $B C$ に関して対称であるから, $\overset{⌢}{P C} = \overset{⌢}{A^{'} C}$ である.従って, $A A^{'}$ はSymmedianである.(この長さに着目した角度の比較はIMOクラスの問題だとよく見かけます.難しいです.)

実践問題3-1

@I_______nu

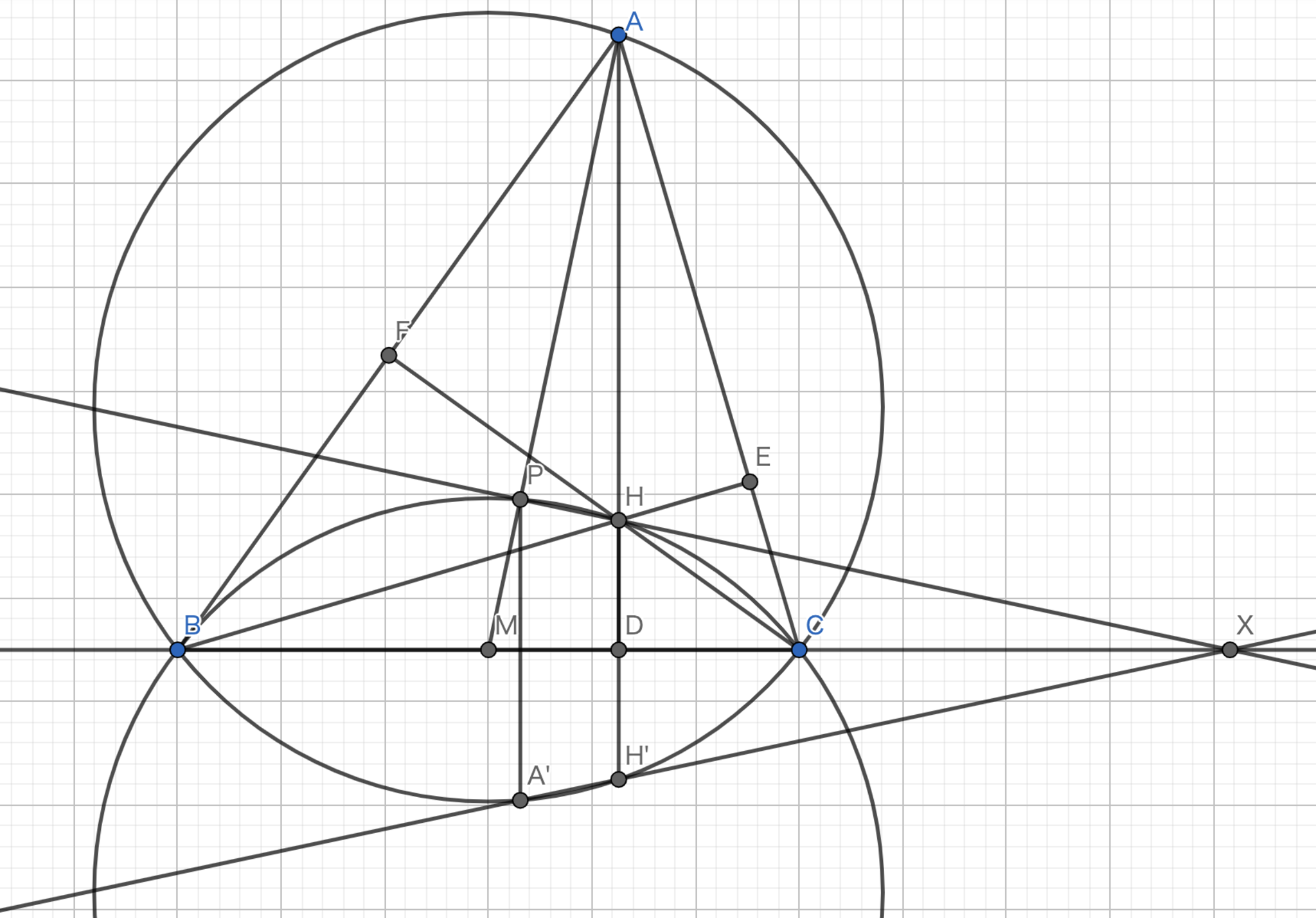
不等辺三角形 $A B C$ において,その外接円を $Ω$ とし, $A$ を通って $B C$ に垂直な直線と $Ω$ の交点のうち $A$ でない方を $D$ とする. $B, C$ から対辺に下ろした垂線の足をそれぞれ $E, F$ とし,三角形 $D E F$ の外接円と $Ω$ の交点のうち $D$ でない方を $A^{'}$ とする. $B^{'}, C^{'}$ も同様に定めるときに $A A^{'}, B B^{'}, C C^{'}$ は一点で交わることを示せ.

引用元はこちら
ヒント:上の問題9と関連しています.

根心の存在性より, $A^{'} D, F E, B C$ は一点 $P$ で交わる. $A M$ と $A H$ の交点を $Q$ とする. $∠ H Q M = 90 °$ ならば問題9より, $A A^{'}$ はSymmedianである.Symmedianは一点で交わるから $∠ H Q M = 90 °$ であることを示せば良い.

ここで, $A A^{″}$ が直径となるように $A^{″}$ をとる.すると, $A B ⊥ A^{″} B$ , $A B ⊥ C F$ であるから $A^{″} B / / C F$ である.同様に $A^{″} C / / B E$ であるから,四角形 $B A^{″} C H$ は平行四辺形である.従って,その中心 $M$ と $A^{″}, H$ は一直線上に並ぶ.ここで,直線 $M H$ と $Ω$ の交点のうち $A^{″}$ でないものを $T$ とすると, $A^{″} T ⊥ A T$ より, $A, F, H, E, T$ は共円である.特にこの円は $A H$ を直径とする円である.この円と $Ω$ , $B, C, E, F$ の外接円の根心を考えれば $A, T, P$ は共線である.ここで, $M T ⊥ A P, A H ⊥ M P$ より, $H$ は三角形 $A M P$ の垂心である.従って, $P H ⊥ A M$ であるから題意は示された.

実践問題4-1

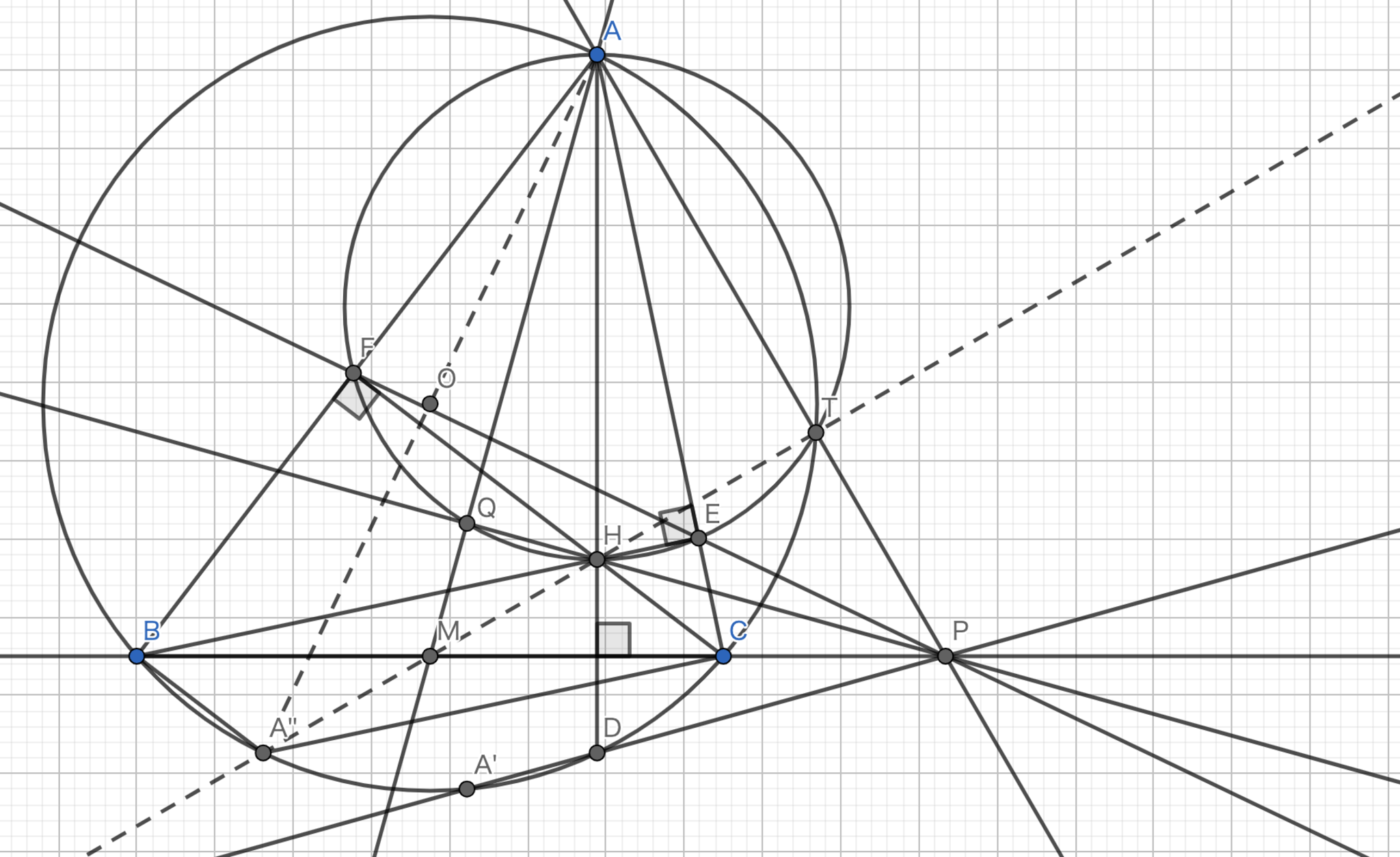実践問題4-2 (これエグいって...)

@I_______nu

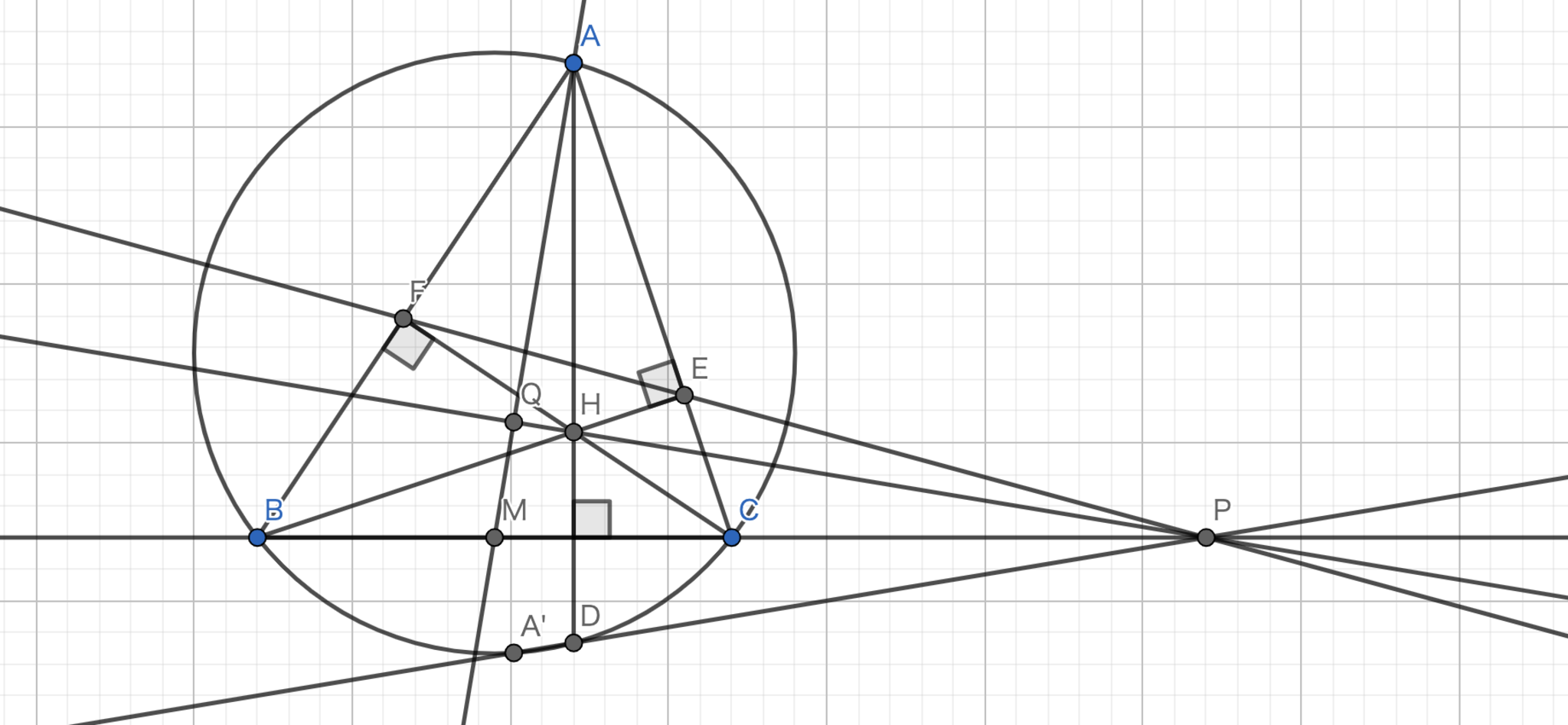
三角形 $A B C$ において, $A$ から対辺に下ろした垂線の足を $D$ , 垂心を $H$ とし, $A H$ を直径とする円と三角形 $A B C$ の外接円 $Ω$ との交点を $P \neq A$ とする. $P D$ と $Ω$ との交点を $F$ とすると, $A F$ はsymmedianであることを示せ.

同様の構図に関する問題です. $A H$ を直径とする円は問題10における $A, F, Q, H, E$ の載る円である.問題10における $T$ と $A^{'}$ と $A$ から $B C$ へと下ろした垂線の足(これを $H_{A}$ とする.)が共線であることを示せば良い.さらに,示すべきことは $∠ Q H_{A} H = ∠ T H_{A} H$ と同値である. $∠ Q H_{A} H = ∠ H M Q = ∠ T M Q = ∠ T P Q = ∠ T P H = ∠ T H_{A} H$ であるから題意は示された.

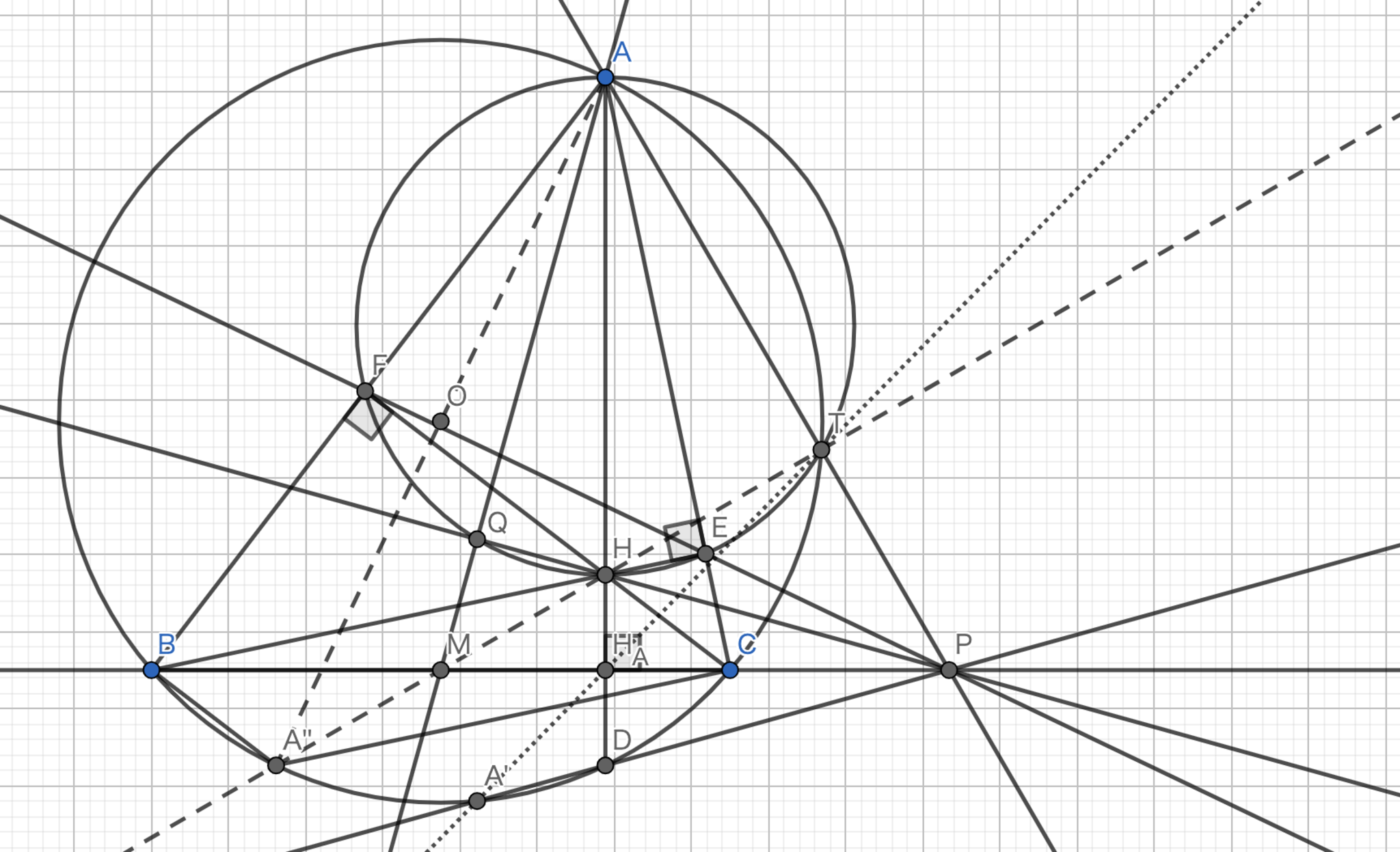問題5-1

この構図における点 $Q$ のことを"Humpty-point"というそうです.

有名構図

三角形 $A B C$ において $B, A$ を $A, C$ へと移す相似拡大の中心を $X$ とする.このとき, $A X$ はSymmedianとなることを示せ.

まずは図を描いて答えを予想してみましょう. $X$ は回転相似の中心ですから $∠ B X A = ∠ A X C$ となります.従って, $∠ B X D = ∠ C X D$ となります.このような点に見覚えはないですか...?そうです,Symmedianの基本性質で扱いましたね. こちらですね.つまり, $X$ は $A D$ の中点かなと予想がつくわけです.というわけで, $A D$ の中点が回転相似の中心となることを示していきます.

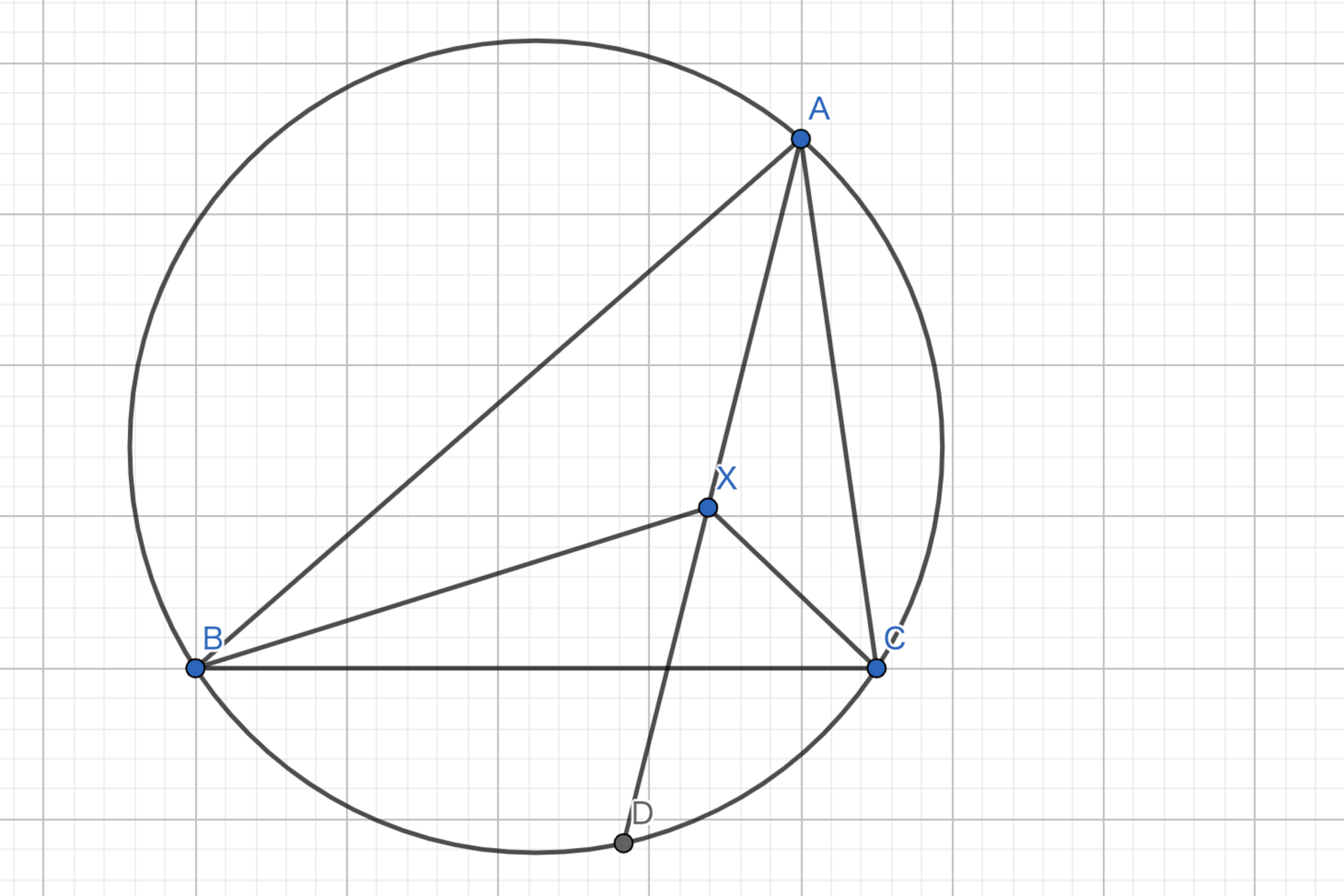実践問題6-1

$A D$ の中点を $X^{'}$ とする. $X^{'}$ が回転相似の中心であることを示せば良い. $B O X^{'} C$ は共円である.Symmedianの性質より, $∠ B X^{'} A = ∠ A X^{'} C$ である.また,四角形 $A B D C$ は調和四角形であるから, $B C$ は三角形 $B D A$ のSymmedianである.従って, $∠ D B C = ∠ A B X^{'}$ である.また,円周角の定理より, $∠ D B C = ∠ D A C$ である.従って, $△ B X^{'} A ∽ △ A X^{'} C$ である. $| B X^{'} | : | A X^{'} | = | A X^{'} | : | C X^{'} |$ より, $X^{'}$ は回転相似の中心である.　

実践問題6-2

ちなみにこのような点を"Dumpty-point"と言うそうです."Humpty-point"と同様に有名な点です.では,この構図を使う問題を見ていきましょう.

USA-TST 2008 Problem7

三角形 $A B C$ の重心を $G$ とする.辺 $B C$ 上に点 $P$ をとり, $Q, R$ を $P Q / / A B, P R / / A C$ となるようにとる.このとき,三角形 $A Q R$ の外接円は常にSymmedian上の一点を通ることを示せ.　

AoPS

$B \to A, A \to C$ となるような回転相似変換 $T$ を考える.問題12より,その中心はSymmedian上の点となる.ここで, $△ R B P ∽ △ Q P C ∽ △ A B C$ であるから, $\frac{R B}{A R} = \frac{R B}{Q P} = \frac{R P}{Q C} = \frac{A Q}{Q C}$ が従う.すなわち, $R, Q$ は $B A, A C$ を等しい比で内分する点であるから変換 $T$ によって, $R$ は $Q$ に移る.従って, $△ A R X^{'} ∽ △ C Q X^{'}$ が得られる.このことから, $∠ A R X^{'} = ∠ C Q X^{'}$ が従う.よって,4点 $A, R, X^{'}, Q$ は共円である.従って,題意は示された.

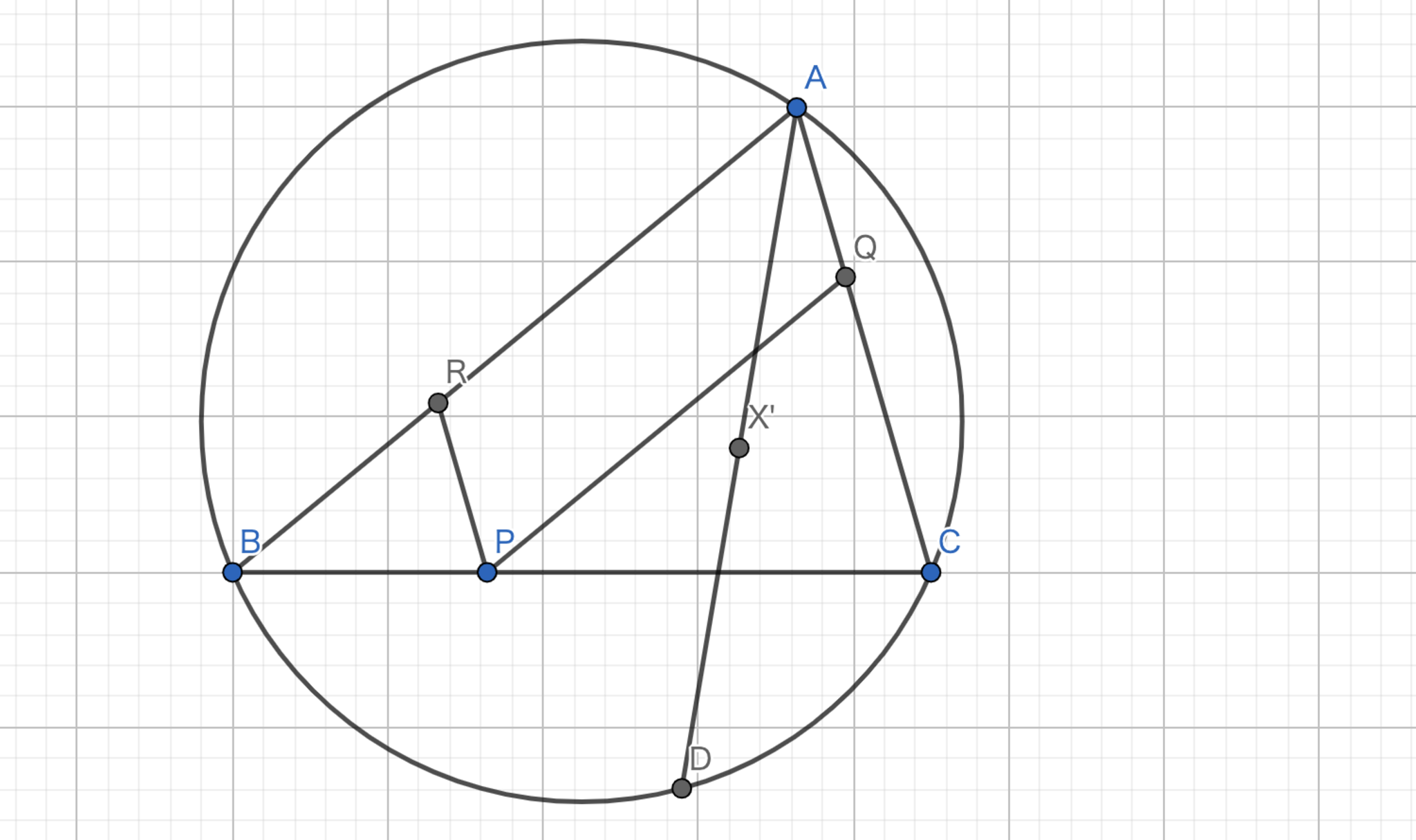実践問題7-1

さて,ここまできた皆さんならば次の問題は簡単に解けるのではないでしょうか.

IMO2003-shortlist G2

一直線上に点 $A, B, C$ がこの順で並んでいる. $A C$ を通る円のうち,中心が線分 $A C$ 上にないものを $Γ$ とする.点 $A, C$ における $Γ$ の接線の交点を $P$ とし, $P B$ は $Γ$ と $Q$ で交わる.このとき,三角形 $A Q C$ の角の二等分線と $A C$ の交点は $Γ$ の選び方に依らないことを示せ.

直線 $P Q$ と $Γ$ の交点のうち, $Q$ でないものを $D$ とすると,四角形 $D A Q C$ は調和四角形となる.従って, $D Q$ は三角形 $D A C$ のSymmedianである.このことから,Steiner's Ratio Theoremより, $| A B | : | C B | = | D A |^{2} : | D C |^{2} ⟺ | \sqrt{A B} | : | \sqrt{C B} | = | D A | : | D C |$ である.また,四角形 $D A Q C$ は調和四角形なので $| D A | \cdot | Q C | = | A Q | \cdot | C D |$ である.これを変形すると, $\frac{| A Q |}{| Q C |} = \frac{| A D |}{| D C |} = \frac{\sqrt{| A B |}}{\sqrt{| B C |}}$ となる.これは三角形 $A Q C$ の角の二等分線と $A C$ の交点が円 $Γ$ に依らないことを意味している.従って,題意は示された.

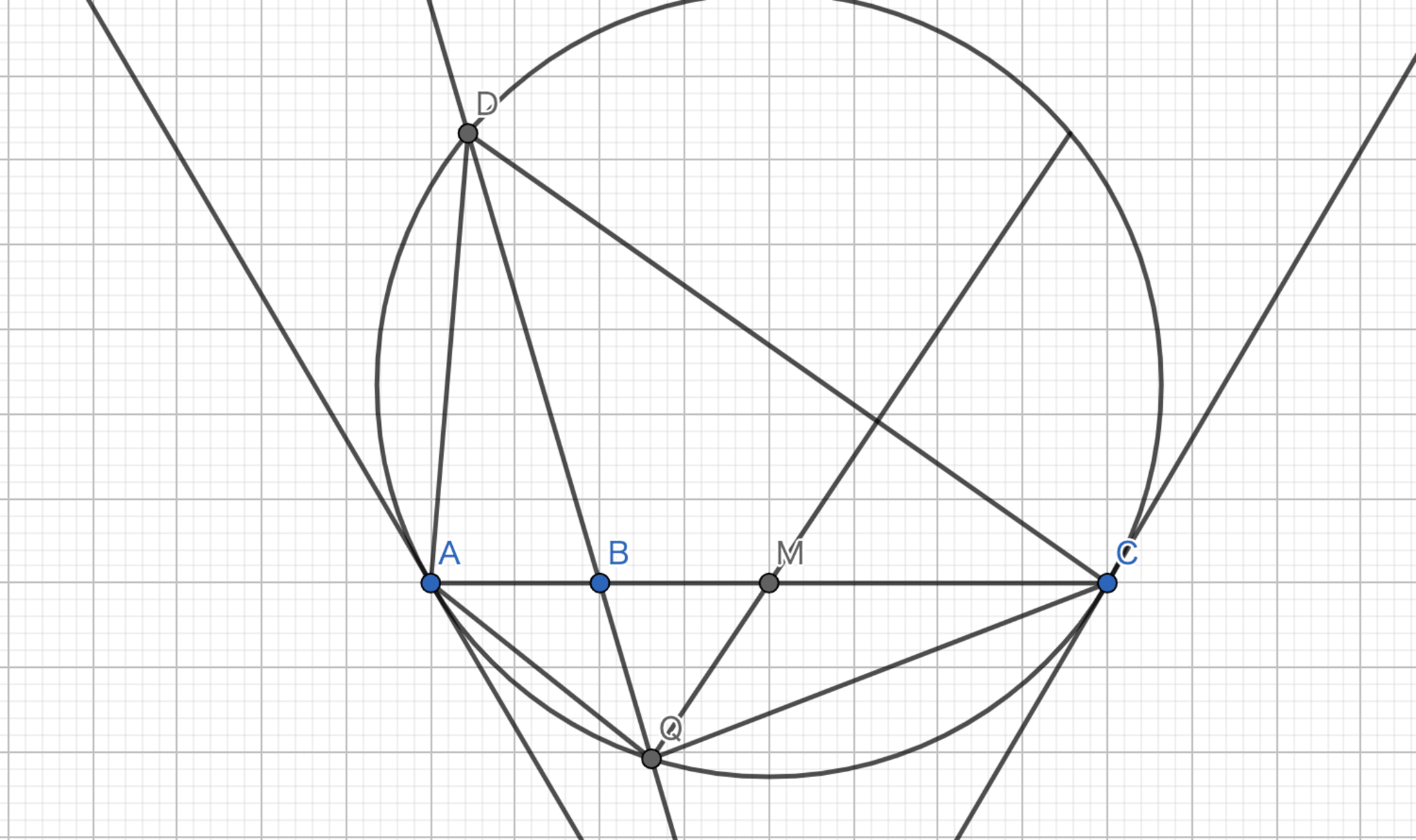実践問題8-1

終わりに

長く拙い記事でしたが,ここまで読んでくださって本当にありがとうございました!少しでも皆さんがSymmedianと仲良くなってくれたらなと思います.行間が広すぎてわからない所やミス等の指摘があればtwitterのDMからいつでも質問してください.あと,高評価を押してくれるととっても嬉しいです!!本当にお願いします!!!

この記事の作成にあたって, 翁さんには大変お世話になりました.ありがとうございました!