Miquelの六円定理
前回の中2の時の投稿からだいぶ間が空きましたが, 今回は初等幾何のちょっとした定理の紹介をします. 証明は難しくないですが, 構図はとても綺麗で気に入っています.
なお, この定理は $\text{Steiner}$の四円定理とも呼ばれています. (
https://link.springer.com/book/10.1007/978-3-642-29163-0
など)
以下の図のように, $4$円のそれぞれが隣接する円と$2$点で交わり, 外側の点をそれぞれ$A,B,C,D$とし, 内側の点をそれぞれ$A', B', C', D'$とする. このとき,
$A, B, C, D$が共円 $\Leftrightarrow$ $A', B', C', D'$が共円
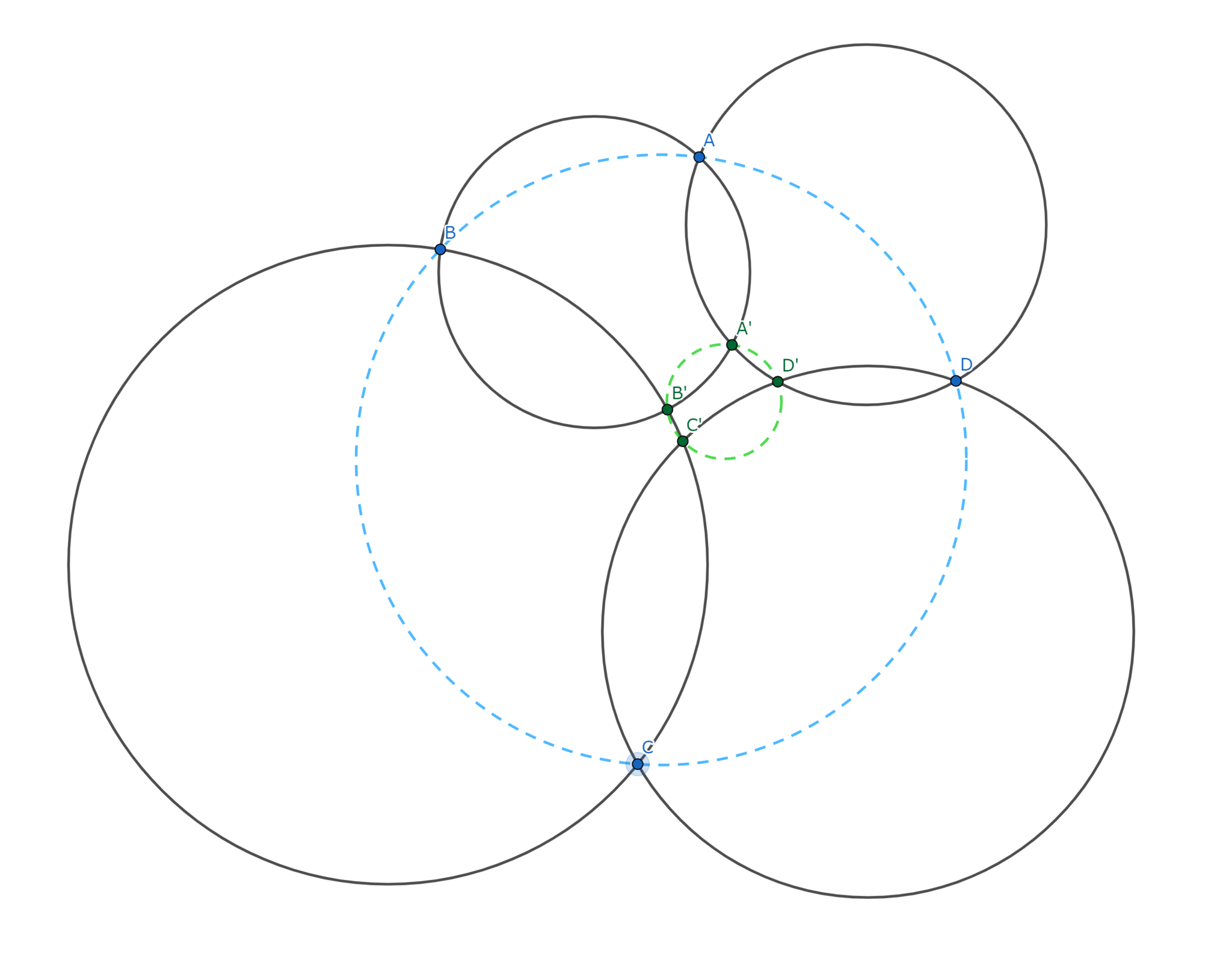Miquelの六円定理
証明は次の図で完結します.
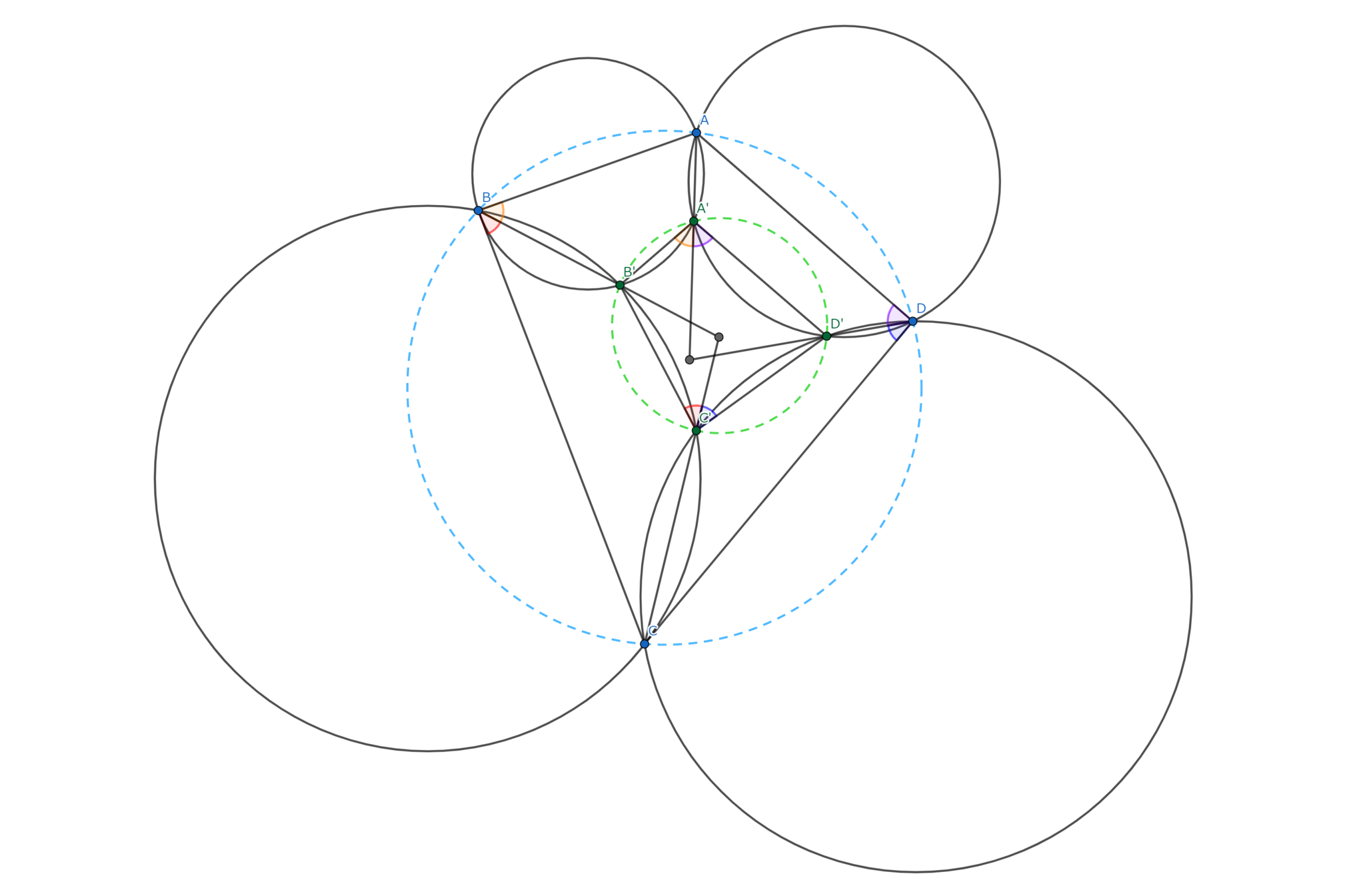proof
四角形$ABCD$の対角の和が$180^{\circ}$ $\Leftrightarrow$ 四角形$A'B'C'D'$の対角の和が$180^{\circ}$
なお, $4$円が接する場合は$4$接点は共円となりますが, これはたぶん$\text{Miquel}$の六円定理には含まれません.
$4$円のそれぞれが隣接する円と接するとき, $4$つの接点は共円となる.
![接する!FORMULA[20][36244][0]円](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220811135944.png?alt=media)
接する$4$円
$A$を中心とした適当な半径の円を固定します. その円について反転をすると$\Gamma_1, \Gamma_2$は平行な$2$直線$\Gamma_1', \Gamma_2'$になり($\because A = P_{\infty}$を通るので), $\Gamma_3, \Gamma_4$は互いに接したまま,それぞれ直線$\Gamma_1', \Gamma_2'$に接する$2$円に移ります. すると, 円外の点から引いた二本の接線は二等辺三角形を成すので$\angle GD'C' = \angle GC'D'$と$\angle IC'B' = \angle IB'C'$が従い, $\Gamma_1' \parallel \Gamma_2'$に留意すれば$B', C', D'$(もちろん$P_{\infty}$も)の共線が導かれ元の$4$点$A, B, C, D$は共円となります.
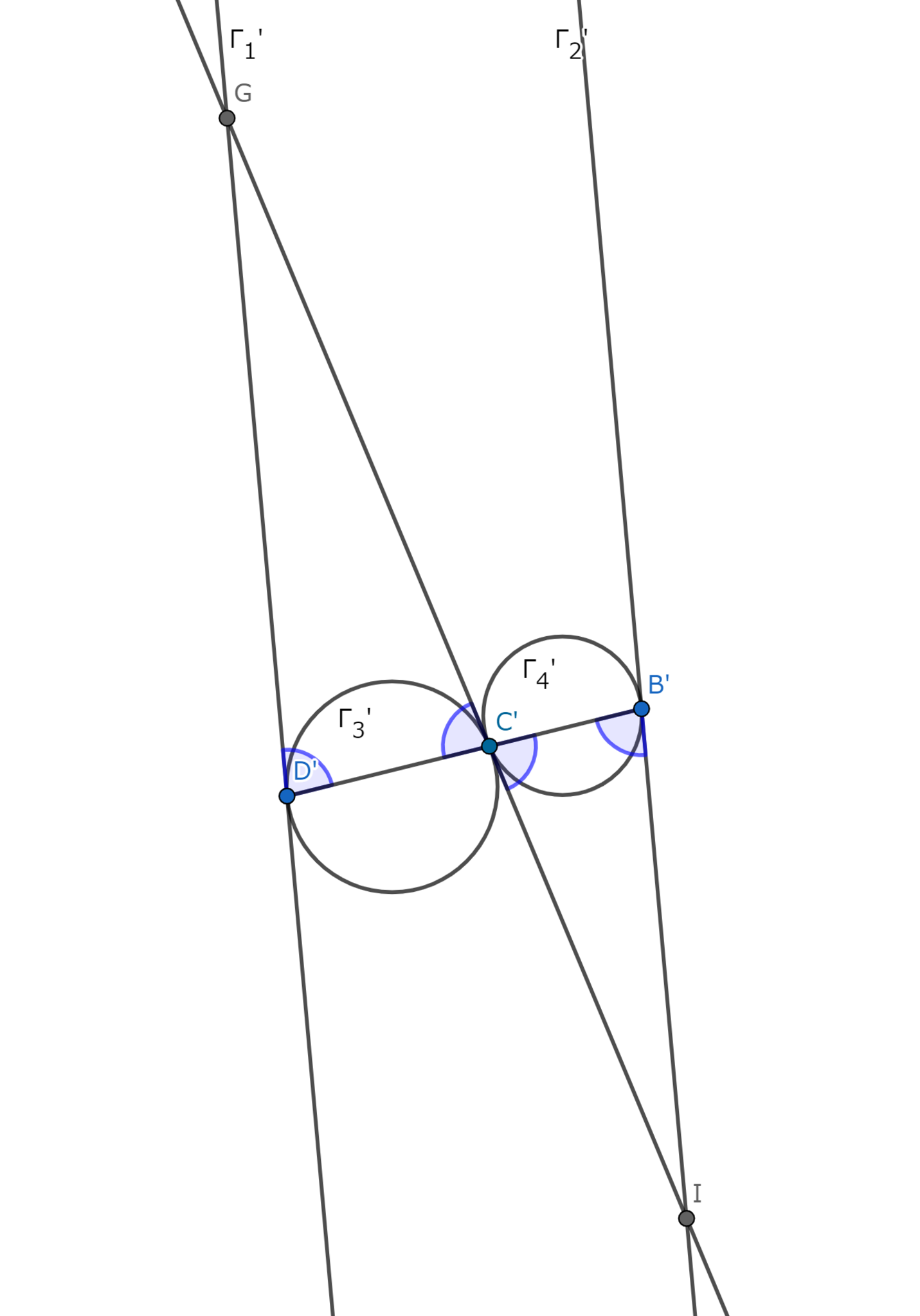†反転†