トレミーの定理を拡張してみた(Ptolemy's theorem)
はじめに
今回はトレミーの定理を拡張していきたいと思います.拡張と言っても,トレミーの不等式ではなく,多角形に拡張していきます.結果が斬新!というよりも,新しい視点でトレミーの定理を見れるようになる.そんな記事です.
事前準備
反転前と後の長さの関係性
$O$を中心とした半径$R$の円で二点$A,B$を反転する.このとき,$$|A'B'|=\frac{R^2}{|OA|\cdot|OB|}\cdot |AB|$$が成り立つ.
ここで,$\triangle{OAB} \backsim \triangle{OB'A'}$であるから,$|AB|:|B'A'|=|OA|:|OB'|=|OA|:\frac{R^2}{|OB|}$である.これを整理することで示したい式を得る.
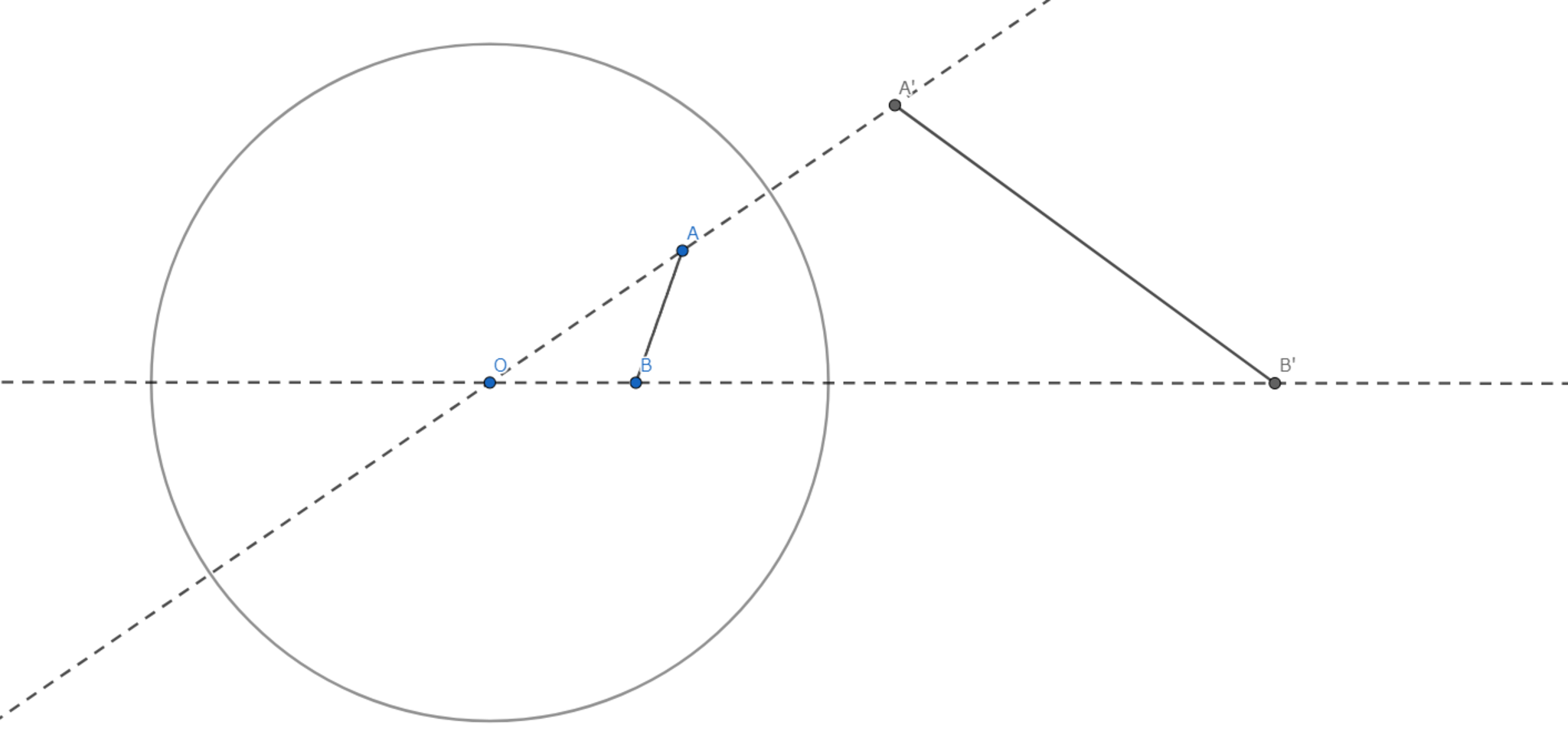三角形の反転
トレミーの定理
円に内接する四角形$ABCD$において,$|AB|\cdot|CD|+|BC|\cdot|DA|=|AC|\cdot|BD|$が成り立つ.
$A$を中心とする半径$1$の円で反転する.(一般性を失わない.)
すると,図のようになり$|B'C'|+|C'D'|=|B'D'|$を得る.ここで,補題1を適用する.
$$
\ \ \ \ \ \ \ \ \ \ \ |B'C'|+|C'D'|=|B'D'| \\
\Longleftrightarrow \frac{R^2}{|AB|\cdot|AC|}\cdot |BC|+\frac{R^2}{|AC|\cdot|AD|}\cdot |CD|=\frac{R^2}{|AB|\cdot|AD|}\cdot |BD| \\
\Longleftrightarrow |AB|\cdot|CD|+|BC|\cdot|DA|=|AC|\cdot|BD|
$$
よって,題意は示された.
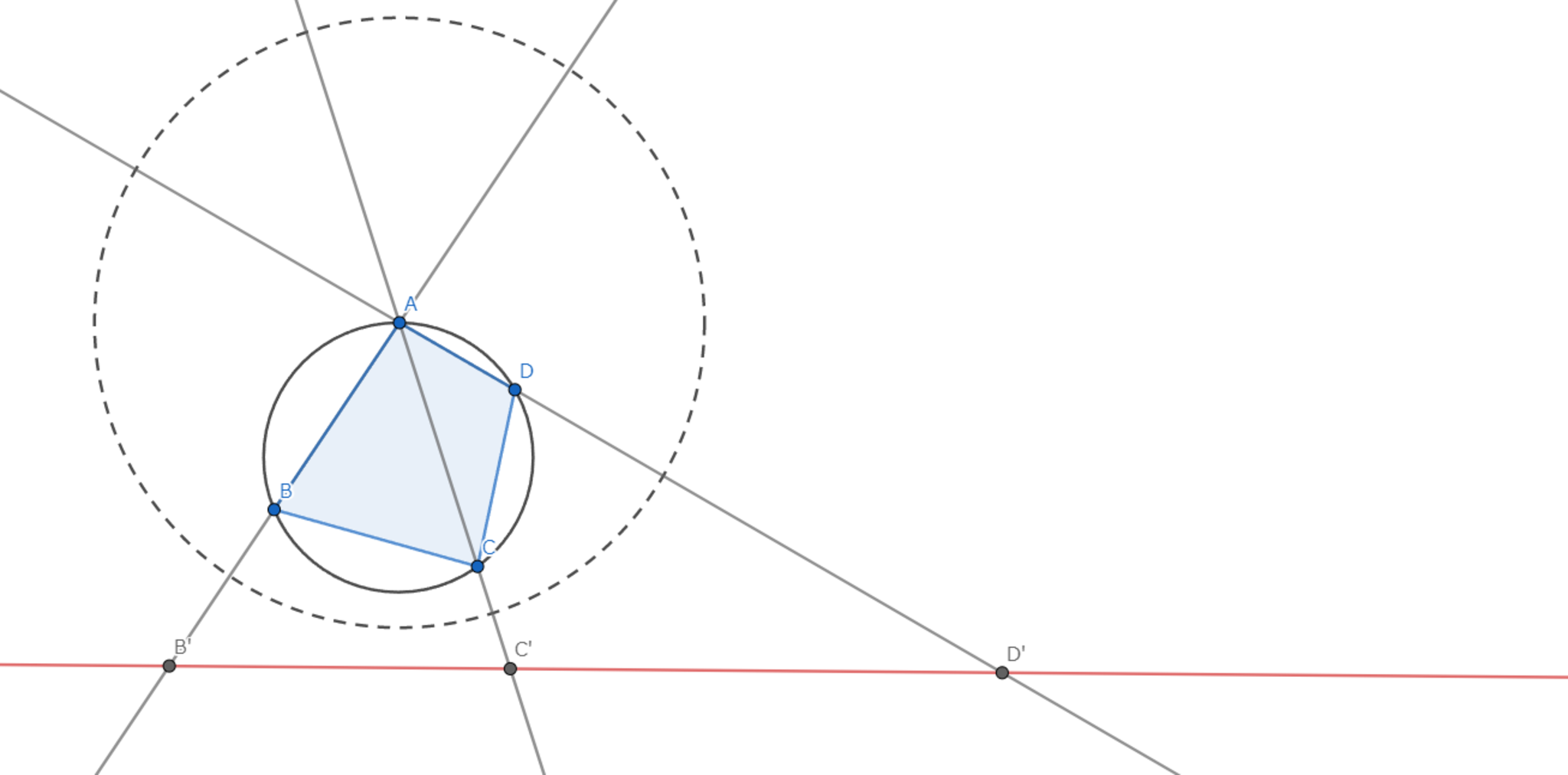トレミーの定理・反転
トレミーの定理の拡張
上記と同様に円に内接する多角形を反転することを考えてみます.この関係式は,反転を用いてトレミーの定理の証明をしないと見えないですね.
円に内接する多角形$A_0A_1A_2\cdots A_{n-1}$において,
$$
\frac{|A_1A_{n-1}|}{|A_{0}A_{1}|\cdot |A_{0}A_{n-1}|}=\frac{|A_{1}A_{2}|}{|A_{0}A_{1}|\cdot |A_{0}A_{2}|}+\frac{|A_{2}A_{3}|}{|A_{0}A_{2}|\cdot |A_{0}A_{3}|}+\cdots+\frac{|A_{i}A_{i+1}|}{|A_{0}A_{i}|\cdot |A_{0}A_{i+1}|}+\cdots+\frac{|A_{n-2}A_{n-1}|}{|A_{0}A_{n-2}|\cdot |A_{0}A_{n-1}|}
$$
が成り立つ.
Aを中心とする円での反転を考える.このとき,$|A_1'A_{n-1}'|=|A_1'A_2'|+|A_2'A_3'|+\cdots+|A_{n-2}A_{n-1}|$が成り立つ.ここに補題1を適用することで示したい式を得る.
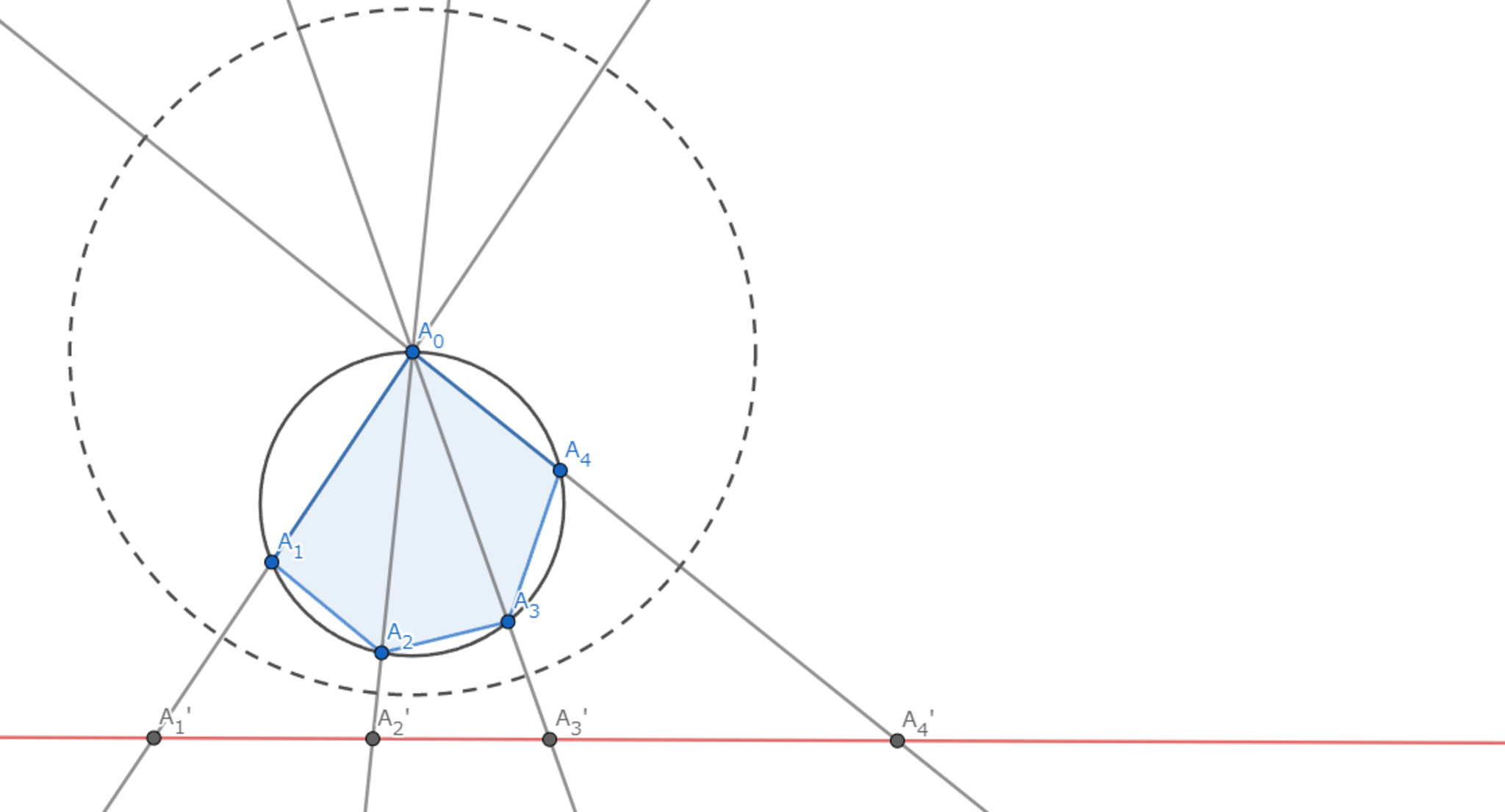n=5の場合
$A_0$に集まる対角線に注目した関係式でした.分母を払えば見た目がトレミーの定理に似た式が出てきます.こう見ると,$n=4$の時は特別でとても綺麗な形をしていることが実感できると思います.通分した式と辺々足した式も置いておきましょう.
円に内接する多角形$A_0A_1A_2\cdots A_{n-1}$において,
$$
\left|A_{1}A_{n-1}\right|\cdot\prod_{i\neq 1,n-1}^{ }\left|A_{0}A_{i}\right|=\sum_{k=1}^{n-2}\left(|A_{k}A_{k+1}|\cdot\prod_{j\neq k,k+1}^{ }\left|A_{0}A_{j}\right|\right)
$$
が成り立つ.
円に内接する多角形$A_0A_1A_2\cdots A_{n-1}$において,
$$
\sum_{i=0}^{n-1}\frac{\left|A_{i-1}A_{i+1}\right|}{\left|A_{i}A_{i-1}\right|\cdot\left|A_{i}A_{i+1}\right|}=\sum_{i=0}^{n-1}\sum_{j\neq i,i-1}^{ }\frac{\left|A_{j}A_{j+1}\right|}{\left|A_{i}A_{j}\right|\cdot\left|A_{i}A_{j+1}\right|}
$$
が成り立つ.
最後に,n=5の場合を鑑賞しましょう.
円に内接する五角形において以下が成り立つ.
$$
\frac{\left|AD\right|}{\left|AE\right|\cdot\left|DE\right|}+\frac{\left|BE\right|}{\left|BA\right|\cdot\left|EA\right|}+\cdots+\frac{\left|EC\right|}{\left|ED\right|\cdot\left|CD\right|}=\left|AB\right|\left(\frac{1}{\left|CA\right|\cdot\left|CB\right|}+\frac{1}{\left|DA\right|\cdot\left|AB\right|}+\frac{1}{\left|EA\right|\cdot\left|EB\right|}\right)+\left|BC\right|\left(\frac{1}{\left|DB\right|\cdot\left|DC\right|}+\frac{1}{\left|EB\right|\cdot\left|EC\right|}+\frac{1}{\left|AB\right|\cdot\left|AC\right|}\right)+\cdots+\left|EA\right|\left(\frac{1}{\left|BE\right|\cdot\left|BA\right|}+\frac{1}{\left|CE\right|\cdot\left|CA\right|}+\frac{1}{\left|DE\right|\cdot\left|DA\right|}\right)
$$
おわりに
結果としてはあまり見た目として綺麗ではなく実用性も薄い結果となってしまいました.しかし,反転を用いて拡張を考えることでトレミーの定理は「ある一点に関する定理の特殊な場合(偶然四角形だと対称的だった)」と捉えられるようになったのではないでしょうか.とても興味深い結果です.拙い文章でしたが読んでいただきありがとうございました!!