文献あり

(相乗平均)≦(対数平均)≦(相加平均)とモローの不等式

941

はじめに

対数平均に関する不等式からモローの不等式を導いてみました。追記：モローの不等式から対数平均の不等式も導けました。
対数平均に関する不等式は[1,4,6,9]、モローの不等式は[2-5]を参考にしています。
対数平均に関する不等式で[10-12]も面白かったです。

対数平均に関する不等式とモローの不等式

平均

正の実数 $x, y$ に対して、
$L = {\begin{array}{cc} \frac{\log y - \log x}{y - x}, & (x \neq y) \\ x & (x = y) \end{array}$ を $x$ と $y$ の対数平均という。
$A = \frac{x + y}{2}, G = \sqrt{x y}$
をそれぞれ $x$ と $y$ の相加平均、相乗平均という。

対数平均に関する不等式

任意の正の実数 $x,$ $y$ に対して、
$A ≧ L ≧ G$
が成り立つ。等号は $x = y$ のときに限り成立する。

定理1の不等式を対数平均に関する不等式と呼ぶことにします。
次に紹介するモローの不等式はネイピア数 $e$ に関する不等式です。

モローの不等式

$0 < x$ に対して、
$\frac{e}{2 x + 2} < e - {(1 + \frac{1}{x})}^{x} < \frac{e}{2 x + 1}$
すなわち、
$\frac{2 x e}{2 x + 1} < {(1 + \frac{1}{x})}^{x} < \frac{(2 x + 1) e}{2 x + 2}$
が成立する。

モローの不等式は、 ${(1 + \frac{1}{n})}^{n}$ が $e$ に収束するのが遅いことを表します。よく知られているように
$e = \sum_{n = 0}^{\infty} \frac{1}{n!}$
と級数表示できます。
$0 ≦ e - \sum_{k = 0}^{n} \frac{1}{k!} = \sum_{k = n + 1}^{\infty} \frac{1}{k!} ≦ \sum_{k = n + 1}^{\infty} (\frac{1}{(k - 1)!} - \frac{1}{k!}) = \frac{1}{n!}$
から分かるようにこの級数の方が収束が速いです。

$f$ は区間 $I$ で定義された連続関数で、 $I$ の内部で微分可能であるとする。導関数 $f^{'}$ が単調増加であるとき任意の $x \in \overset{˚}{I}$ と $c \in \overset{˚}{I}$ に対して、
$f (x) ≧ f^{'} (c) (x - c) + f (c)$
が成立する。 $f^{'}$ が狭義単調増加であるときは、 $x = c$ のときに限り等号が成立する。

命題3は下に凸な関数y=f(x)は接線y=f'(c)(x-c)+f(c)によって支持されることを表します。

$f^{'}$ が狭義単調増加の場合の証明を書く。
$f (x) = f (c) + \int_{c}^{x} f^{'} (t) d t .$
(曲線y=f(x)を折れ線近似して極限をとった等式？)
と書ける。(i) $c < x$ のとき $f^{'} (c) < f^{'} (x)$ であるから積分の単調性より、 $f (x) > f (c) + \int_{c}^{x} f^{'} (c) d x = f^{'} (c) (x - c) + f (c) .$
(ii) $x < c$ のときも同様である。
(iii)x=cのとき等式が成立することは明らかである。

命題3から基本的で便利な不等式が得られます。

$α < 0$ または $1 < α$ のとき、 $(1 + x)^{α} > 1 + α x$ ( $- 1 < x, x \neq 0$ )
$\sin x < x < \tan x (0 < x < π / 2)$
$\sinh x > x > \tanh x (0 < x)$
$e^{x} > 1 + x (x \neq 0), \log (1 + x) < x (- 1 < x, x \neq 0)$
( $\log (1 + x) < x$ は $e^{x} > 1 + x$ の両辺に自然対数をとれば得られます。)

例1の文字を置き換えて遊んでみよう。
(i)で $α = 2$ とすると $(1 + x)^{2} > 1 + 2 x$ $(- 1 ≦ x, x \neq 0)$ .
$- 1 / 2 ≦ x, x \neq 0$ のとき右辺は非負であり両辺を $1 / 2$ 乗すると、
$\sqrt{1 + 2 x} < 1 + x$ . $x$ を $\frac{x}{2}$ で置き換えると、

$\sqrt{1 + x} < 1 + \frac{1}{2} x (- 1 ≦ x, x \neq 0) .$

(iv)の最初の不等式で $x$ を $x - 1$ で置き換えて両辺に $e$ を掛ける、二つ目の不等式で $x$ を $(x / e) - 1$ で置き換えて両辺に $1$ を加えると次が得られます。

$e^{x} > e x (x \neq 1), \log x < \frac{x}{e} (0 < x \neq e) .$

これらの不等式は後で使います。

モローの不等式の左側
$\frac{2 x e}{2 x + 1} < {(1 + \frac{1}{x})}^{x}$
と $\sqrt{1 + x} < 1 + \frac{1}{2} x$ から
$e < {(1 + \frac{1}{x})}^{x + \frac{1}{2}}$
が得られる。この不等式は東京大学の入試問題でも出題された。また、高校数学の美しい物語>微分を用いた不等式証明の問題の不等式
$0 < (x + \frac{1}{2}) \log (1 + \frac{1}{x}) - 1 < \frac{1}{4 x (x + 1)} (1 ≦ x)$
の左側と同値である。右側はモローの不等式の右側
${(1 + \frac{1}{x})}^{x} < \frac{2 x + 1}{2 x + 2} e$
に対数をとって、 $\log x ≦ x / e$ を利用すると得られる。

同じような文字の置き換えと簡単な操作から次の例のような不等式が得られます。

$0 < β < 1$ のとき $(1 + x)^{β} < 1 + β x (- 1 ≦ x)$
$1 < α$ のとき $x^{α} > α (x - 1) + 1$ $(0 < x, x \neq 1)$
$c > 0$ のとき $x^{α} > α c^{α - 1} (x - c) + c^{α - 1} (0 < x, x \neq c)$
$e^{x} > e^{c} (x - c) + e^{c} (x \neq c)$
$e^{x} > e x (x \neq 1), \log x < \frac{x}{e} (x \neq e)$
$α > 0$ のとき $e^{x} > (e / α)^{α} x^{α} (0 ≦ x, x \neq α)$
$0 < α$ のとき $\log x < \frac{x^{α}}{e α} (0 < x, x \neq e^{1 / α})$

\sinh x > x > \tanh x (0 < x)

を利用した対数平均に関する不等式(定理1)の証明

不等式 $\sinh x > x > \tanh x$ $(0 < x)$ において、 $x$ を $\log x$ で置き換える。
$\begin{array}{r} \frac{x - \frac{1}{x}}{2} > \log x > \frac{x - \frac{1}{x}}{x + \frac{1}{x}} (1 < x) \end{array}$
$0 < a < b$ として $x = b / a$ と置いてみる。不等式は
$\begin{array}{r} \frac{b^{2} - a^{2}}{2 a b} > \frac{\log b^{2} - \log a^{2}}{2} > \frac{b^{2} - a^{2}}{b^{2} + a^{2}} \end{array}$
と書ける。
$a$ , $b$ をそれぞれ $\sqrt{a}$ , $\sqrt{b}$ で置き換えて、 $b - a > 0$ で割ると、
$\begin{array}{r} \frac{1}{\sqrt{a b}} > \frac{\log b - \log a}{b - a} > \frac{2}{a + b} . \end{array}$
各辺は正であるから、逆数をとると不等号の向きが逆になり、定理の不等式が得られる。

イェンセンの不等式(積分形)

$a < b$ , $g (x)$ は区間 $[a, b]$ 上の積分可能な関数、
$f (x)$ は $g$ の値域 $g ([a, b])$ を含む区間の内部で微分可能であり、 $f^{'} (x)$ は単調増加であるとする。 $p (x) > 0$ で $\int_{a}^{b} p (x) d x = 1$ であるとする。そのとき、
$\begin{array}{r} \int_{a}^{b} f (g (x)) p (x) d x ≧ f (\int_{a}^{b} g (x) p (x) d x) \end{array}$
が成立する。
$f^{'}$ が狭義単調増加であるとき、不等式の等号が成立するための必要十分条件は $g$ がほとんどいたるところ定数になることである。

$f^{'}$ が狭義単調増加, $g$ が連続ならば等号成立条件は $g$ が定数関数であること。

$c = \int_{a}^{b} g (x) p (x) d x$ とおく。 $p$ に関する条件から $c$ は $f$ の定義域( $g ([a, b])$ を含む区間)の点であることに注意する。命題3より、
$f (g (x)) ≧ f^{'} (c) (g (x) - c) + f (c)$
が成立する。両辺に $p (x) (> 0)$ を掛けて、 $x$ に関して $a$ から $b$ まで積分すればよい。

イェンセンの不等式（数列形）

$n = 1, 2, . . .$ を自然数、 $p_{i} > 0$ $(i = 1, . . ., n)$ は $\sum_{i = 1}^{n} p_{i} = 1$ を満たすとし、 $f$ は区間 $I$ の内部で微分可能で $f^{'}$ は単調増加であるとする。任意の $x_{i} \in I$ $(i = 1, . . ., n)$ に対して、
$\sum_{i = 1}^{n} p_{i} f (x_{i}) ≧ f (\sum_{i = 1}^{n} p_{i} x_{i})$
が成立する。 $f^{'}$ が狭義単調増加であれば、不等式の等号が成立する必要十分条件は $x_{1} = \dots = x_{n}$ である。

証明は積分形と同様にできる。積分形とは $x_{i} \leftrightarrow g (x)$ , $p_{i} \leftrightarrow p (x)$ と対応する。積分形で数え上げ測度をとったものと考えてもよい。

Hermite-Hadamard inequality

$f$ は閉区間 $[a, b]$ 上で連続、開区間 $(a, b)$ で微分可能でその導関数 $f^{'}$ は単調増加であるとする。そのとき、
$f (\frac{a + b}{2}) ≦ \frac{1}{b - a} \int_{a}^{b} f (x) d x ≦ \frac{f (a) + f (b)}{2}$
が成立する。 $f^{'}$ が狭義単調増加であれば、不等号" $≦$ "は"<"として成立する。

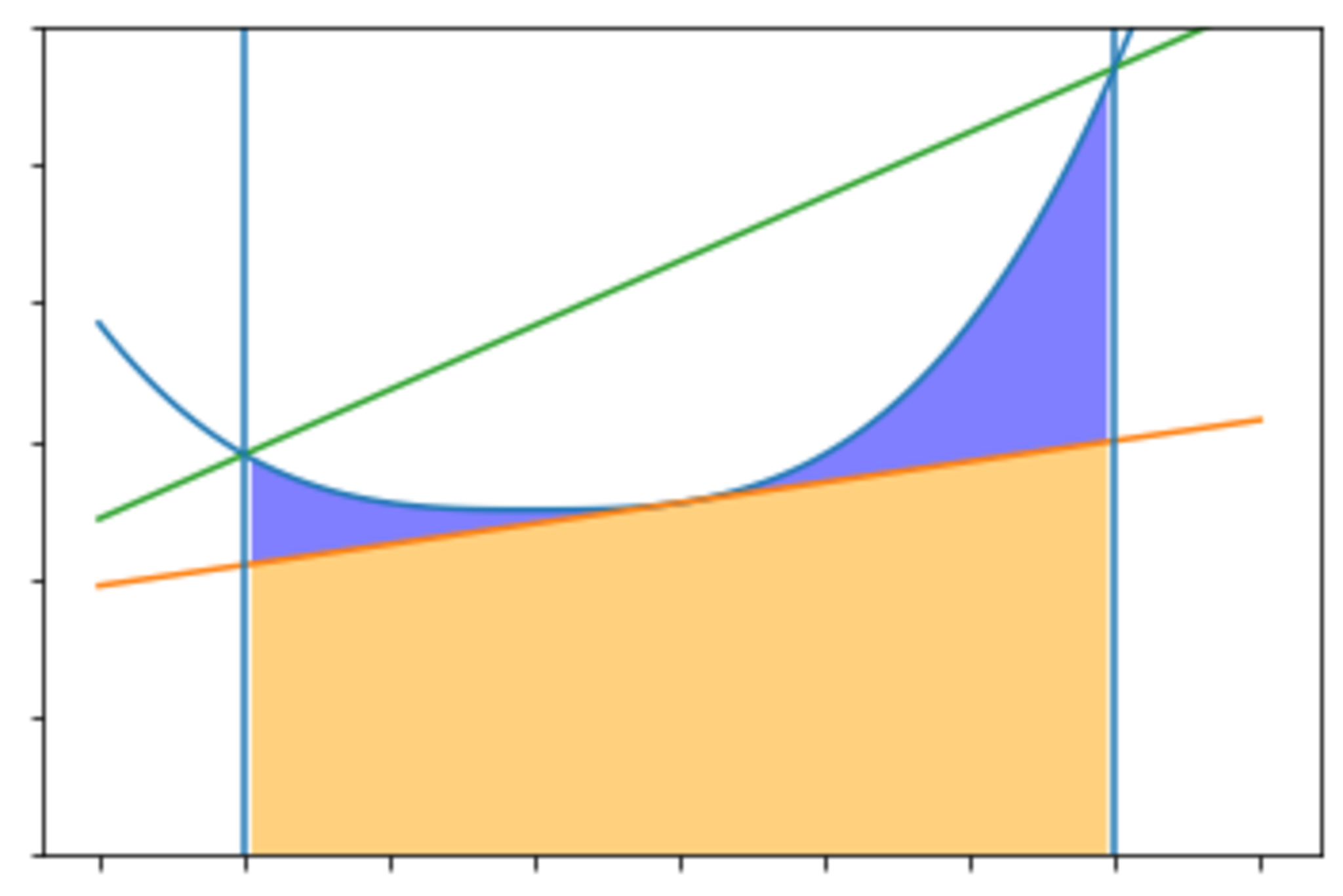Hermite-Hadamardの不等式(左側)

Hermite-Hadamardの不等式(右側)

左側の不等式は $g (x) = x$ , $p (x) = 1 / (b - a)$ としてイェンセンの不等式を適用すればよい。右側の不等式を示す。イェンセンの不等式より、
$f (\frac{x + y}{2}) ≦ \frac{f (x) + f (y)}{2}$
が成立することに注意する。
$\begin{aligned} \frac{1}{b - a} \int_{a}^{b} f (x) d x & = \frac{1}{b - a} \int_{a}^{b} \frac{f (x) + f (a + b - x)}{2} d x \\ ≦ \frac{1}{b - a} \int_{a}^{b} f (\frac{a + b}{2}) d x \\ = f (\frac{a + b}{2}) . \end{aligned}$

(

\log x

にHermite-Hadamard inequalityを適用した定理2(モローの不等式)の証明)

$\begin{aligned} \log {(1 + \frac{1}{n})}^{n} & = n \log (n + 1) - n \log n \\ = \int_{n}^{n + 1} \log x d x - \log (n + 1) + 1 \\ = \int_{n}^{n + 1} \log \frac{e x}{n + 1} d x \end{aligned}$
Hermite-Hadamardの不等式より、
$\begin{aligned} \frac{1}{2} (\log \frac{e (n + 1)}{n + 1} + \log \frac{e n}{n + 1}) & < \int_{n}^{n + 1} \log \frac{e x}{n + 1} d x \\ < \log (\int_{n}^{n + 1} \frac{e x}{n + 1} d x) . \end{aligned}$
すなわち、
$\begin{array}{r} \log \frac{e}{\sqrt{1 + \frac{1}{n}}} < \log {(1 + \frac{1}{n})}^{n} < \log (\frac{(2 n + 1) e}{2 n + 2}) . \end{array}$
左辺に
$\sqrt{1 + \frac{1}{n}} < 1 + \frac{1}{2 n}$
を使い、真数を比較するとモローの不等式が得られる。

対数平均に関する不等式の証明で

y = e^{x}

にHermite-Hadamardの不等式を適用する方法

$x = \log a, y = \log b$ と置いてHermite-Hadamardの不等式を適用すればよい。

対数平均に関する不等式の証明には他にもあります。興味があれば[1,5]を見てください。

対数平均の不等式に関する証明で

y = 1 / x

にHermite-Hadamardの不等式を適用する方法

$\log b - \log a = \int_{a}^{b} d x / x .$
$a$ と $b$ の調和平均を $H := \frac{2 a b}{a + b}$ とおく。
Hermite-Hadamardの不等式より、
$H ≦ L ≦ A$
が得られる。失敗したかと思うが、あきらめないで、左側の不等式で $a, b$ を $\sqrt{a}, \sqrt{b}$ で置き換えて、 $\sqrt{a} + \sqrt{b}$ を掛ければよい。
（なぜ指数関数に対してHermite-Hadamardの不等式を適用する方が上手くいくのか？？）

対数平均に関する不等式(定理 1)は接線を利用して得られる対数関数の不等式 $\log (1 + x) ≦ x$ では不十分なとき、次に考えると便利です。対数平均に関する不等式からモローの不等式を導いてみよう。

対数平均に関する不等式からモローの不等式を導く

対数平均に関する不等式(定理1)より、
$\begin{array}{r} \frac{2 n}{2 n + 1} < \log {(1 + \frac{1}{n})}^{n} < \frac{n}{\sqrt{n (n + 1)}} \end{array}$
左側の不等式と $x > \log (e x)$ から、
$\begin{array}{r} \frac{2 n e}{2 n + 1} < {(1 + \frac{1}{n})}^{n} . \end{array}$
右側の不等式を考える。
$\begin{aligned} \frac{n}{\sqrt{n (n + 1)}} & = \sqrt{1 - \frac{1}{n + 1}} \\ = 1 - \int_{0}^{\frac{1}{n + 1}} \frac{1}{\sqrt{2 (1 - x)}} d x \\ < 1 - \int_{0}^{\frac{1}{n + 1}} \frac{1}{2 - x} d x \\ = \log \frac{(2 n + 1) e}{2 n + 2} . \end{aligned}$
よって、モローの不等式の右側
${(1 + \frac{1}{n})}^{n} < \frac{(2 n + 1) e}{2 n + 2}$
が得られる。

モローの不等式から対数平均に関する不等式

モローの不等式の右側
${(1 + \frac{1}{x})}^{x} < \frac{2 x + 1}{2 x + 2} e$
は次のように変形できる。
${(1 + \frac{1}{x})}^{x + \frac{1}{2}} < \frac{2 x + 1}{2 \sqrt{x (x + 1)}} e .$
右辺に不等式 $e x ≦ e^{x}$ を適用すると、
${(1 + \frac{1}{x})}^{x + \frac{1}{2}} < e^{\frac{2 x + 1}{2 \sqrt{x (x + 1)}}} .$
対数をとって整理すると、
$\log (x + 1) - \log x < \frac{1}{\sqrt{x (x + 1)}} .$
したがって、
$\sqrt{x (x + 1)} < \frac{1}{\log (x + 1) - \log x} .$
$0 < a < b$ の場合を考えればよい。 $x = \frac{a}{b - a}$ とおくと、 $G < L$ を得る。モローの不等式の左側
$\frac{2 x e}{2 x + 1} < {(1 + \frac{1}{x})}^{x}$
から
$e < {(1 + \frac{1}{x})}^{x + \frac{1}{2}}$
が得られることは上記の注意で示した。対数をとって整理すると、
$\frac{1}{\log (x + 1) - \log x} < \frac{2 x + 1}{2}$
$x = \frac{a}{b - a}$ とおくと、 $L < A$ を得る。