外心と傍心を結ぶ直線に垂直な直線

635

はじめに

三角形 $A B C$ において, その外心を $O$ , 角 $A$ 内の傍心を $J$ とし, $A B$ と角 $C$ の二等分線との交点を $D$ , $A C$ と角 $B$ の二等分線との交点を $E$ とします. このとき, $D E ⊥ O J$ が成り立つ, という有名(とされている)事実があります. こちらのツイートで, これについての自分なりの証明をいくつかの問題に分けて出したので, この記事では解答という形でそれを示していきます. また, 関連する問題や話題にも触れるつもりなのでぜひ最後まで目を通していってください！
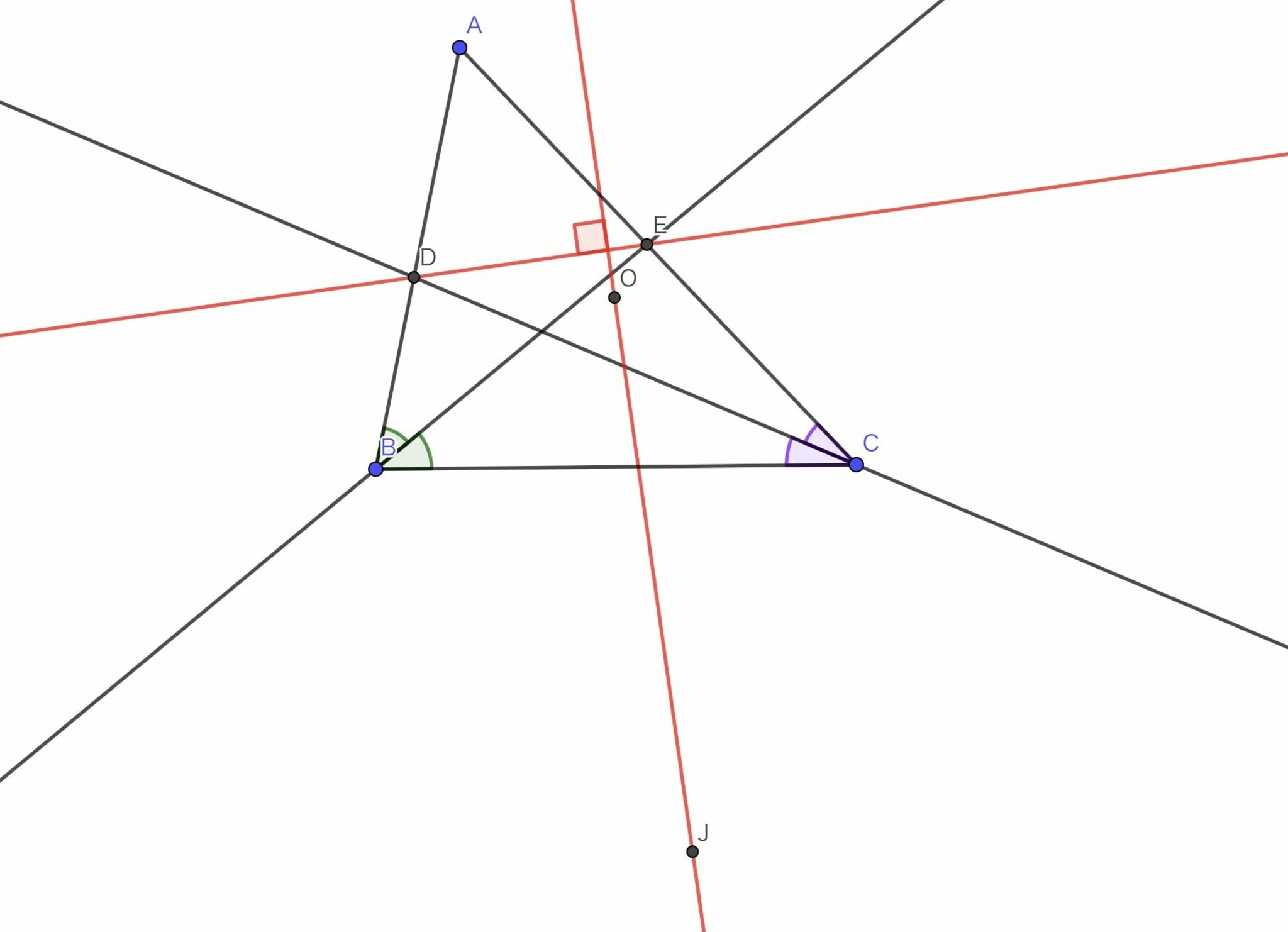命題の図

証明

パート $1$

このパートでは以下の補題を示します.

$A B, A C$ 上に $F, G$ を, $B C = B F = C G$ が成り立ち, かつ $A, B, F$ と $A, C, G$ がそれぞれこの順で並ぶようにとる. このとき $D E$ と $F G$ は平行である.

補題!FORMULA[19][36151][0] 補題 $1$

辺の長さをいろいろ計算して, $A D : A E = A F : A G$ を示せばよさそうです.

$B C = a, C A = b, A B = c$ とおく. $A F = a + c, A G = a + b$ であり, 角の二等分線と辺の比の関係から $A D = \frac{b c}{a + b}, A E = \frac{b c}{a + c}$ を得るので, $A D : A E = A F : A G$ が得られ, 題意は示された.

ここで $B E$ と $C D$ の交点を $I$ とすると, $I$ は三角形 $A B C$ の内心です.

パート $2$

このパートでは以下の補題を示します.

三角形 $A B C$ の外接円と三角形 $A F G$ の外接円の交点を $U (\neq A)$ , $A I$ と三角形 $A F G$ の外接円の交点を $V (\neq A)$ とすると, $F G ⊥ U V$ である.

補題!FORMULA[38][36182][0] 補題 $2$

これは, とある構図を知っていればすぐに示すことができます.

構図 $1$

三角形 $A B C$ において, 辺 $A B, A C$ 上の点 $D, E$ が $B D = C E$ をみたす. このとき三角形 $A B C$ の外接円と三角形 $A D E$ の交点を $M (\neq A)$ とすれば, $M$ はそれぞれの円において弧 $B A C$ , 弧 $D A E$ の中点である.
構図!FORMULA[50][36151][0] 構図 $1$

これは, 図4において三角形 $M D B$ と $M E C$ が合同であることを示せば証明できます. この構図と, 図3において $V$ が三角形 $A F G$ の外接円における $A$ を含まない方の弧 $F G$ の中点であることから, $U V$ が $F G$ の垂直二等分線であることがわかり, 補題 $2$ は示されました.

ここから証明の本筋からはそれた話題をあつかうので, 証明だけ見たい人はパート $3$ までとばしてください.

このパートで出てきた構図 $1$ について, もうひとつだけ似たような見た目の構図を紹介します.

構図 $2$

平面上の $5$ 点 $A, B, C, D, M$ が, $A B = C D$ , $B C$ の中点が $M$ , $A, D, M$ はこの順に同一直線に並ぶ, という条件を全て満たすとき, $∠ B A M = ∠ C D M$ が成り立つ.
構図!FORMULA[70][36182][0] 構図 $2$

これは, 図5において $M$ に関して $D$ と対称な点をとって角度を追うことで示すことができます.

以上の話題に関連した問題をいくつか集めてみたので, よければ見ていってください. 答えはここには記さないので, 気になったら質問してください.

自作

三角形 $A B C$ において, 辺 $A B, A C$ 上の点 $D, E$ が $B D = C E$ をみたす. 三角形 $A B C$ の外接円と三角形 $A D E$ の交点を $L (\neq A)$ , $B C$ の中点を $M$ , $D E$ の中点を $N$ , $A N$ と三角形 $A B C$ の外接円の交点を $K (\neq A)$ としたとき, $K, L, M, N$ が同一円周上にあることを示せ.

問題!FORMULA[88][36151][0] 問題 $1$

JMO2003 本選 1

三角形 $A B C$ の内部に点 $P$ をとり, 直線 $B P$ と辺 $A C$ の交点を $Q$ , 直線 $C P$ と辺 $A B$ の交点を $R$ とする. $A R = R B = C P$ かつ $C Q = P Q$ であるとき, $∠ B R C$ の大きさを求めよ.

問題!FORMULA[100][36182][0] 問題 $2$

IMO SLP 2015 G1

$A B C$ を, 垂心を $H$ とする鋭角三角形とする. $G$ を, 四角形 $A B G H$ が平行四辺形であるような点とし, $I$ を, $G H$ 上の点であって $A C$ が $H I$ を二等分するような点とする. $A C$ が三角形 $G C I$ の外接円と $C, J$ で交わっているとするとき, $I J = A H$ を示せ.

問題!FORMULA[113][36213][0] 問題 $3$

パート $3$

このパートでは以下の補題を示します.

三角形 $A B C$ について, その外心を $O$ , 角 $A$ 内の傍心を $J$ , 外接円と $A I$ との交点を $T (\neq A)$ としたとき, $U V$ と $O J$ は平行である.

補題!FORMULA[123][36213][0] 補題 $3$

今までの結果から $O$ が $T U$ の中点であることはすぐわかるので, $J$ が $T V$ の中点であることを示せば中点連結定理から題意が従います. 実は $B F, C G$ の中点をそれぞれ $M, N$ として, $A, M, J, N$ が同一円周上にあることを示せれば $J$ が $T V$ の中点であることは従います.

補題!FORMULA[133][36213][0]の証明補題 $3$ の証明
$B F, C G$ の中点をそれぞれ $M, N$ とする. $J B, J C$ はそれぞれ角 $F B C, G C B$ を二等分するから, 三角形 $J B C, J B F, J G C$ はすべて合同である. よって三角形 $J B M, J G N$ が合同であることもわかり, $∠ M J N = 2 ∠ B J C$ がわかるので, 角度計算から $∠ M A N + ∠ M J N = 180^{\circ}$ を得る. したがって $A, M, J, N$ は共円である.

また, 三角形 $A B C, A M N, A F G$ それぞれの外接円において円周角の定理を用いて角度を追うことにより, 三角形 $U B F, U T V, U C G$ がすべて相似であり, 三角形 $U B M, U T J, U C N$ がすべて相似であることがわかる. $M, N$ はそれぞれ $B F, C G$ の中点であるから, 対応辺の比により $J$ が $T V$ の中点であることもわかる.

$T O = O U, T J = J V$ であるから, 中点連結定理より $O J$ と $U V$ が平行であることがわかり, 補題 $3$ は示された.

以上から, $D E ⊥ O J$ であることがわかります. めでたしめでたし！

以降の内容は完全におまけです.

二円が二点で交わっていて, 一点を通る直線がいくつかあったときに, もう一点を中心としていくつかの相似な三角形が回転しているかのようにならぶ, このパートでも登場した相似を回転相似といいます. この回転相似や, 相似な図形上の対応する点に注目する, という手法はときどき使うので知っておいて損はないでしょう. これまたいくつか問題を集めてみたので, よければ見ていってください.

Thailand Mathematical Olympiad 2019 8

$A B C$ を $A B \neq A C$ を満たす三角形とし, その外接円を $ω$ とする. $I$ を三角形 $A B C$ の内心とし, 三角形 $A B C$ の内接円と $B C$ との接点を $D$ とする. $A I$ を直径とする円と $ω$ の交点を $K \neq A$ とし, $A I$ と $ω$ との交点を $M (\neq A)$ としたとき, $K, D, M$ は一直線上に並ぶことを示せ.

問題!FORMULA[170][36244][0] 問題 $4$

Spain Mathematical Olympiad 2022 3

$A B C$ を, $A B < A C$ をみたす三角形とし, その外接円を $Γ$ とする. 内接円と辺 $B C, C A, A B$ との接点をそれぞれ $D, E, F$ とし, $D$ から $E F$ に下ろした垂線の足を $R$ , 角 $B A C$ の外角の二等分線と $Γ$ との交点を $S (\neq A)$ とする. $A R$ と $S D$ は $Γ$ 上で交わることを示せ.

問題!FORMULA[185][36275][0] 問題 $5$

おまけ

今までは扱ってきた命題に絡めて幾何の構図などを紹介してきましたが, ここではこの命題そのものと絡んだ話題をあつかっていきたいと思います.

自作

補題 $3$ と同様に点を定め, $I$ と $O$ の中点を $S$ としたとき, $O J$ と $S T$ が平行であることを示せ.

問題!FORMULA[192][36306][0] 問題 $6$

自作

問題 $6$ と同様に点を定め, また三角形 $A B C$ の外接円と $B I, C I$ との交点をそれぞれ $Q (\neq B), P (\neq C)$ , $P Q$ と $B C$ との交点を $R$ としたときに, $I R ⊥ S T$ を示せ.

問題!FORMULA[201][36337][0] 問題 $7$

JMO2020 本選 2

$B C < A B$ , $B C < A C$ なる三角形 $A B C$ の辺 $A B, A C$ 上にそれぞれ点 $D, E$ があり, $B D = C E = B C$ をみたしている. 直線 $B E$ と直線 $C D$ の交点を $P$ とする. 三角形 $A B E$ の外接円と三角形 $A C D$ の外接円の交点のうち $A$ でない方を $Q$ としたとき, 直線 $P Q$ と直線 $B C$ は垂直に交わることを示せ.

問題!FORMULA[217][36368][0] 問題 $8$

おわりに

ここまで読んでくださりありがとうございました. また問題を追加するかもしれません.

投稿日：2022年10月2日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

翁

4044

他の人のコメント

コメントはありません。

読み込み中

翁

外心と傍心を結ぶ直線に垂直な直線

はじめに
証明
パート$1$
パート$2$
パート$3$
おまけ
おわりに

外心と傍心を結ぶ直線に垂直な直線

はじめに

証明

パート1

パート2

構図1

構図2

パート3

おまけ

おわりに

この記事を高評価した人

この記事に送られたバッジ

投稿者

コメント

他の人のコメント

パート $1$

パート $2$

構図 $1$

構図 $2$

パート $3$