n個の立方体にも1個の立方体にもなる展開図に関する未解決問題に挑戦(部分解決)
はじめに
この記事では「 $n$ 個の立方体にも $1$ 個の立方体にもなる展開図」に関するとある未解決問題に挑戦します!
(2022.10.24 記事を大幅に加筆修正しました。)
(2022.10.29 「おわりに$3$」を加筆しました。)
きっかけとなったツイート
まずはコチラをご覧ください。@panlepan さんのツイートの「4個の立方体にも1個の立方体にもなる展開図」
From 2 cubes to 1 (bigger) cube.🤩 idea & animation by Rinus Roelofs !
— Vincent Pantal🍩ni (@panlepan) October 17, 2022
Source on fb :https://t.co/n7sSInsdtG pic.twitter.com/q5wFb6kL1I
 4
4
続いて同じく@panlepan さんのツイートから「5個の立方体にも1個の立方体にもなる展開図」
If you enjoyed this, wait till you see the version with 5 cubes !https://t.co/zlG4bFkP2m pic.twitter.com/BNiRDDrnNB
— Vincent Pantal🍩ni (@panlepan) October 17, 2022
 5
5
これらのツイートに触発されて私も考えてみました。「2個の立方体にも1個の立方体にもなる展開図」
印刷してみたの図
— apu (@apu_yokai) October 19, 2022
想定どおりに組むことができたよ!
🎉☺️🎉 pic.twitter.com/77iTXTOizg
 2
2
レプ・キューブとは
このように、$n$ 個の立方体にも $1$ 個の立方体にもなる展開図は「レプ・キューブ」と呼ばれています。レプ・キューブは $2016$ 年に生まれたまだ新しい概念です。
それ自体が立方体を折れて,かつそれぞれが立方体を折れる $k$ 個のポリオミノに分割できるようなポリオミノを次数 (order) $k$ の「レプ・キューブ (rep-cube)」と呼ぶ。
「ポリオミノ」というのは「複数の正方形を辺でつなげた多角形」のことです。よく見る立方体の展開図やテトリスのブロックの形などがポリオミノの例になります。
次に「正則」について説明します。
特に $k$個がどれも同じ面積になるものを「正則なレプ・キューブ(regular rep-cube)」という。
「なぜ『正則』を考えるの?」と疑問に思われる方もいると思います。実は、レプ・キューブの中には、異なる面積に分割できるようなものが存在するので、議論を明確にするためにこのような定義をしています。
 次数50の正則なレプ・キューブの例(「計算折り紙入門」から引用)
次数50の正則なレプ・キューブの例(「計算折り紙入門」から引用)
あらためて冒頭のツイートを見ると、いずれも正則なレプ・キューブであることがわかりますね。
なお、この記事では「正則なレプ・キューブ」についてのみ考察します。(非正則なレプ・キューブについて考えるのも楽しそうですが)
レプ・キューブについての注意点
ここで一つ注意点を上げたいと思います。「レプ・キューブ」のポリオミノを分割するとき、必ずしも正方形$6$個からなる、ようするに「普通の」展開図の形に分割するとは限りません。
正直にいうと、私も最初勘違いしていました。
特に、ここまでの例ではどれも正方形6個のポリオミノに分割していましたのでそんな風に思ってしまいそうですが、もっと複雑な形のポリオミノに分割するケースもあり得るということです。
予想と未解決問題
さて、正則なレプ・キューブとなりうるような分割方法について、どのような性質がなりたつでしょうか。
遊んでいるうちに、次の予想を思いつきました。
(予想)
— apu (@apu_yokai) October 20, 2022
「n個の立方体にも1個の立方体にもなる展開図」は
n=2,4,5,8,9,10,13のときは可能
n=3,6,7,11,12のときは不可能 https://t.co/6iwknfUJbV
先にこの数列についてタネ明かしすると、「可能」の方は「$2$ つの平方数の和で表せるもの」、「不可能」の方は「$2$ つの平方数の和で表せないもの」です。「$2$ つの平方数の和で表せる」とは、次のように表すことができるということです。
$2=1^2+1^2$
$4=2^2+0^2$
$5=2^2+1^2$
$8=2^2+2^2$
$9=3^2+0^2$
$10=3^2+1^2$
$13=3^2+2^2$
こんな感じです。
このツイートをしたところ、 @alytile さんに、「計算折り紙入門」という本にこの問題について書かれていることを教えていただきました。
(なお、ここから下の記事で単に「本」と書いている場合は、この本のことだと思ってください。)
そして、この「不可能」の方の数列について、その本で未解決問題として紹介されていることがわかりました。
この本の8章にrepcubeの話がまとまっています。https://t.co/EYlLH79pSw
— 荒木義明 (@alytile) October 20, 2022
全く同じことが書いてあった😁 https://t.co/qlWTlrYKuM pic.twitter.com/0c12uBFGte
— apu (@apu_yokai) October 22, 2022
 「計算折り紙入門p.177」
「計算折り紙入門p.177」
未解決問題についての私の勘違い(このパートは読み飛ばしても良いです)
ここで、私が考えていた数列と全く同じものがでてきたので、この部分を読んだとき私は「自分の予想が未解決問題として掲載されている!」と無邪気に考えてしまいましたが、実はそれは勘違いでした。
私はこのとき、「$n$個の立方体にも$1$個の立方体にもなる展開図」について考えていたのですが、「分割された展開図は正方形 $6$ 個からなるポリオミノ」で、「組み合わせて$1$個の立方体にすることさえできれば、展開図を合体して$1$個のポリオミノにならなくてもいい」という条件で、「$n$ としてあり得る数字、あり得ない数字は何か」について考えていました。
よく似た問題設定なので同じ数列が出てきたわけですが、実は異なる問題設定だったというわけです。
この記事では、当初私が考えていた問題ではなく、本に記載されている方の未解決問題についての私の考えを書いています。(その後で、私が考えていた問題の解答についても簡単に触れています。)
証明すべき命題
本に記載されている未解決問題は、こういうものでした。
与えられた自然数 $k$ に対して、正則な次数 $k$ のレプ・キューブが存在するかどうかを高速に判定する方法があるだろうか。
何が解決済みで何が未解決か
前提として、この本では$k=2,4,5,8,9,10,13,16,17,18,20,\ldots $といった二平方和となる数は正則なレプ・キューブが存在しそうな数であるとして、$k=2,4,5,8,9,25,36,50,64$ の場合は実際に構成することで存在を証明しています。
$k=3,6,7,11,12,14,15,19,21,22,23,\ldots$ といった二平方和とならない数は、正則なレプ・キューブは存在しないと考えられるとしつつ、 $k=3$ の場合のみ存在しないことを証明し、「一般の数について統一的に扱う方法は、未解決である。」としています。
注意点として、ここで「未解決」としているのは、分割したポリオミノが必ずしも正方形 $6$ 個で構成されているとは限らないことが前提となっているからであり、分割したポリオミノが正方形 $6$ 個からなる場合に次数が二平方和とならないレプ・キューブが存在しない事は、既知と考えてよいでしょう。
この記事で証明の目標とする命題
この記事では、「$k=3,6,7,11,12,14,15,19,21,22,23,\ldots$といった二平方和とならない数は、正則なレプ・キューブは存在しない」ことを証明することを目標としています。
さらに進んで、「二平方和となる数を次数とする正則なレプ・キューブが存在する」ことまで証明できれば未解決問題を完全解決することができるというわけですが、「可能」であることを証明するためには具体的な構成方法を考えないといけないと思いますので、とてもめんどくさそう……なので、今回は挑戦しません(すいません)。
とはいえ、「存在しないことを証明するほう」は、本にも書いてあるとおり、存在することを証明するよりは簡単にできそうです。
というわけで、この部分についての証明に挑戦します!
証明すべき命題を整理すると、次のようになります。
$2$ 以上の自然数 $K$ は $2$ つの平方数の和で表すことができない $\Rightarrow$ 次数 $K$ の正則なレプ・キューブは存在しない。
証明
まず補題をいくつか考えます。
定理といくつかの補題
証明の準備を始めましょう。
まず、「フェルマーの二平方和定理」をご紹介します。
$2$ つの整数 $x,y$ を用いて $n=x^2+y^2$ と表される
$\Leftrightarrow$ $n$ を素因数分解したときの $4k+3$ 型の素数の指数が全て偶数
フェルマーの二平方和定理を使うと「$n$ を $2$ つの平方数の和で表せる」という性質は「$n$ を素因数分解したとき、$4k+3$ 型の素数の指数が偶数」と言い換えることができるというわけです。
実際、$2,4,5,8,9,10,13$ の$4k+3$ 型の素数の指数が偶数で、 $3,6,7,11,12$ の$4k+3$ 型の素数の指数が奇数であることを確認してみてください。
立方体 $Q$ の展開図が $P$ であったとき、 $Q$ で頂点だった点は $P$ の外周上にある。
$Q$ の頂点回りの面の角度の和は $270$ 度であるから、展開図にカットする線は必ず $Q$ の頂点をとおらなければならない(頂点でカットし終わる場合を含む)。
※ 本の定理 $2.1.3$ とほぼ同じです。
ポリオミノ $P$ が立方体 $Q$ の展開図となっているとする。
$Q$ の頂点に対応する位置の $P$ の外周上の点は $1$~$3$ 個あり、そのうち少なくとも1つは$180$°ではない。
$Q$ の頂点の位置を切り開くときの組合せは、($270$°)か($180$°,$90$°)か($90$°,$90$°,$90$°)のいずれかであることから従う。
ポリオミノ $P$ が立方体 $Q$ の展開図となっているとする。
ポリオミノの単位正方形の大きさの正方格子を描く。正方格子の格子点に $P$ の頂点がすべて乗るように$P$ を重ねたとき、$Q$ の頂点に対応する位置の $P$ の外周上の点もすべて正方格子の格子点に乗る。
$Q$ の頂点を切り開いて $P$ を作るところを想像すればよい。補題$4$ より切り開かれる面のうち少なくとも $1$ つは $90$°又は $270$° であるから、頂点は必ず格子点に乗る。
先ほどの図$4$ でも、$Q$ の頂点にあたる位置が格子点に乗っていることを確認してみてください。
証明
それでは証明パートに入ります。
まず、次のような操作を考えます。
$P$ を次数 $K$ のレプ・キューブとし、$P$ から作られる立方体を $Q$ とする。
$P$ を$K$ 個に分割したポリオミノたちを $p_1,p_2,\ldots,p_K$ とし、それらから作られる立方体を $q_1,q_2,\ldots,q_K$ とする。
$q_1$ の表面上に対応する $p_1$ を「印刷」し、ポリオミノの単位正方形を基準とする正方格子の上で$q_1$ をサイコロのように転がしながらスタンプのように展開図を「印刷」する操作を考える。
正方格子の格子点上に、$p_1$ の各頂点が乗るように「印刷」していくと、$q_1$ の頂点に対応する$p_1$の外周上の点もまた格子点に乗る。
しつこいようですが、$p_i$ が単位正方形$6$ 個で構成されているとは限らないことに注意してください。
複雑な形のポリオミノの場合もあるということです。
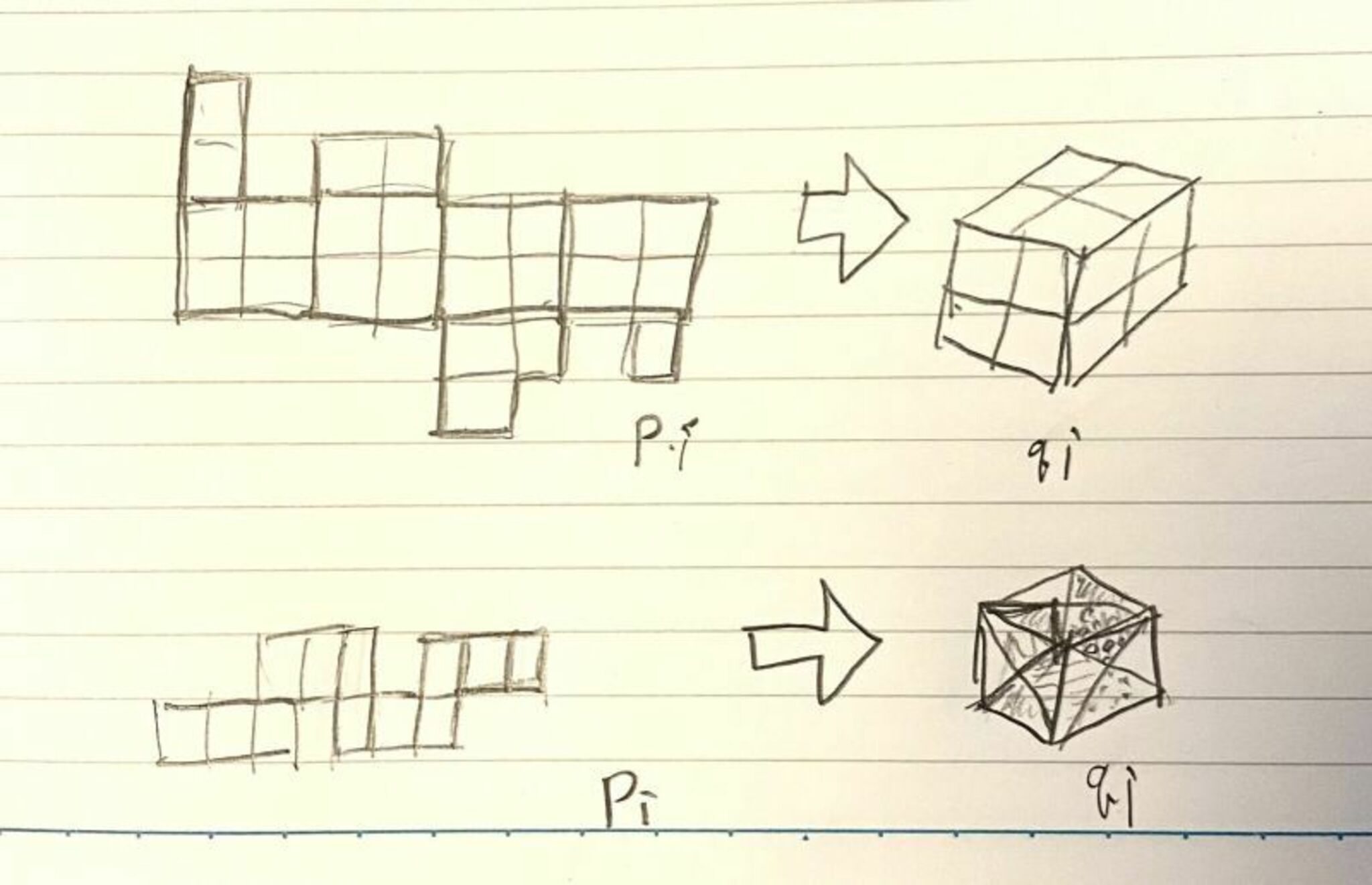 正方形6個ではない例
正方形6個ではない例
そのうえで、ここで考えている正方格子は、$q_i$ の一辺の長さではなく、あくまで$P$ や $p_i$ を構成するポリオミノの単位正方形を基準とする正方格子ということです。
ここからは、説明をわかりやすくするため、$q_1$ の展開図 $p_1$ を紙で作っているものとして説明します。
$q_1$ の表面上に対応する $p_1$ を印刷し、スタンプのようにしてさきほどの正方格子上を転がすことを考えます。
$q_1$ の辺を一つ選び、辺 $AB$ とします。辺 $AB$ をはさむ $2$ 面を正方格子上に、各 $p_1$ の頂点が正方格子上にのるように、下図のようにスタンプすると、少なくとも $1$ つの面で頂点$A,B$にそれぞれ対応する位置の $p_1$ の頂点($180$°ではない)と重なることから、頂点$A,B$もまた正方格子上になければならないことになります。
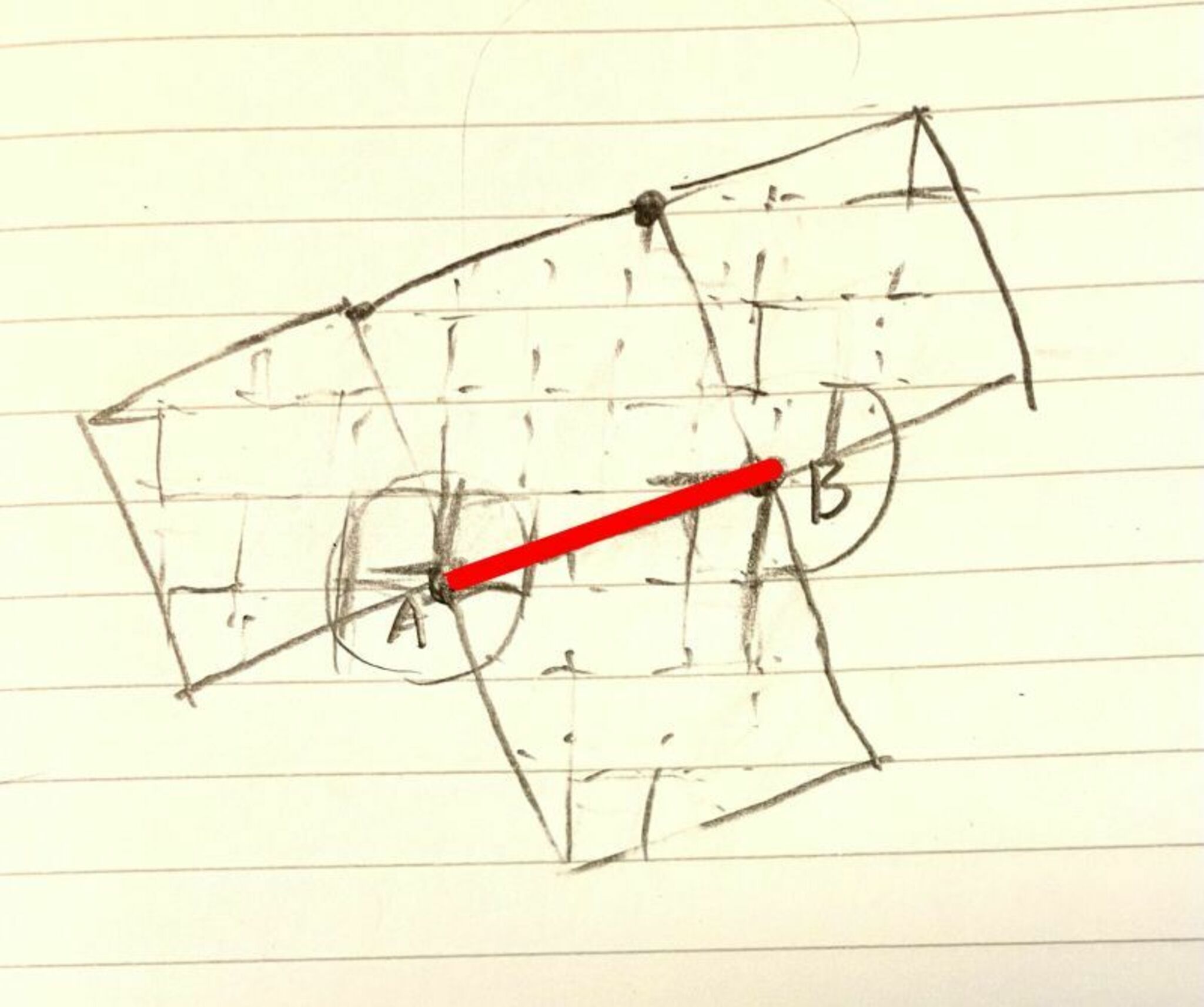 「スタンプ」で「印刷」するイメージ
「スタンプ」で「印刷」するイメージ
正方格子は単位正方形と同じ大きさ$1$とします。
正方格子を「$A$を原点とする座標平面」とみなしたときの $B$の座標を $(a,b)$ とします($a,b$ は整数)。
三平方の定理より、$AB=\sqrt{a^2+b^2}$ なので、立方体 $q_1$ の$1$つの面の面積を $s_1$ とすると
$s_1=a^2+b^2$
となります。
フェルマーの二平方和定理より、 $s_1$ は $4k+3$ 型の素数の指数が偶数であることがわかります。
次に、分割前の $P$ で同様の操作を行います。
$p_1$ のすべての頂点が格子点に乗るように配置したとき、分割前の $P$ を($p_1$ の位置が分割に対応するように)格子点に乗せると、$P$ のすべての頂点が格子点に乗り、対応する$p_2,\ldots,p_k$ のすべての頂点も格子点に乗る。
ポリオミノの性質からこれは明らかですね。
参考として先ほどの例を再掲します。
 (再掲)次数50の正則なレプ・キューブの例(「計算折り紙入門」から引用)
(再掲)次数50の正則なレプ・キューブの例(「計算折り紙入門」から引用)
さあ、証明完了まであと少しです!
立方体 $Q$ の$1$つの面の面積を $S$ とします。
先ほどと同様の議論から、$S$ も $4k+3$ 型の素数の指数が偶数であることがわかります。
レプ・キューブの次数が $K$ であることから、
$S=K\cdot s_1$
となります。
$s_1$ も $S$ も $4k+3$ 型の素数の指数が偶数であることから、$K$ も $4k+3$ 型の素数の指数が偶数であるとわかります。
したがって、フェルマーの二平方和定理より、$K$ は $2$ つの平方数の和で表すことができます。
以上より、正則なレプ・キューブの次数 $K$ は必ず $2$ つの平方数の和で表すことができると言えましたので、その対偶をとって、
$2$ 以上の自然数 $K$ は $2$ つの平方数の和で表すことができない $\Rightarrow$ 次数 $K$ の正則なレプ・キューブは存在しない。
は真であることがわかりました!
一般化
実は、「$p_1,p_2,\ldots,p_K$が単位正方形$6$つを辺でつないでできた立方体の展開図である」という条件があれば、$P$がポリオミノであるという条件をなくしても、$p_1,p_2,\ldots,p_K$をつないで$1$個の大立方体$Q$を作ることができるのは「 $K$ が $2$ つの平方数の和で表すことができる」場合に限られることを証明することができます。
(実のところ、当初私が考えていた問題はこちらの方でした。)
ここではおおまかな方針だけを示します。
・小展開図のパターンは $11$ 種類。どのパターンも $6$ 個以上の凸部($90$ 度の部分)と $2$ 個以上の凹部($270$ 度の部分)がある
・小展開図を $1$ つ選び、その頂点が重なるようにグリッドを配置する。
・大展開図の頂点でない位置に凸部又は凹部がある場合は、隣接する小展開図で同じグリッドにのるものが必ずあるから、これを次々に連結してカタマリを大きくしていく。この時、カタマリの頂点はすべてグリッドにのる。
・最終的にはすべてが$1$つにつながりヒトカタマリになる。このことは、「長方形のカタマリをつくることができないこと」と、「凸部も凹部もないカタマリはベルト状になる」ことからいえる。
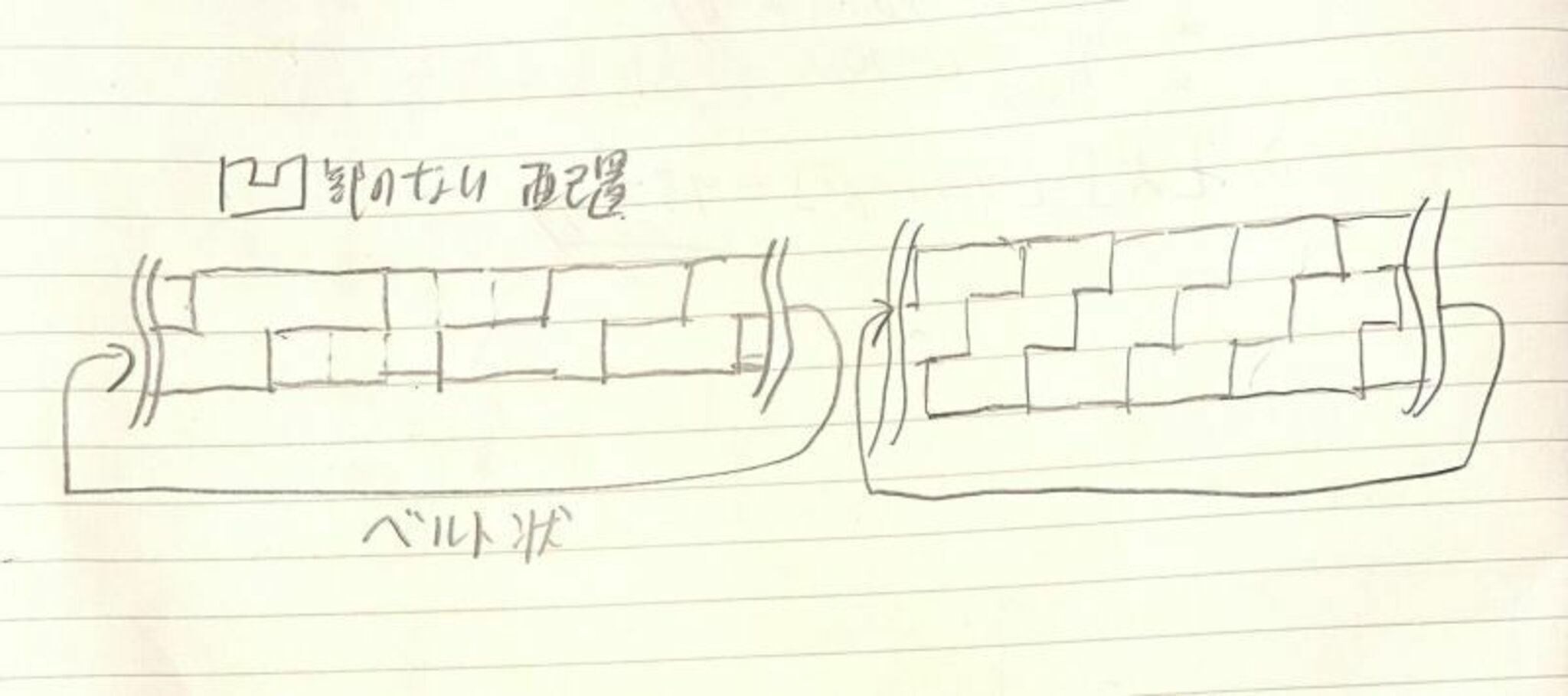 ベルト状の配置
ベルト状の配置
・カタマリの上に大立方体の展開図を重ねるとき、大立方体の展開図の角はグリッドにのっていなければならない
・したがって 大立方体の表面積=小立方体の表面積*((整数)²+(整数)²)
おわりに
以上、未解決問題を部分的に解決できました・・・
・・・
・・・
・・・と思います。多分。
正直なところ、「未解決問題がそんなに簡単に解決できるわけないから、何か致命的な見落としがあるのでは?」という気持ちがかなりあります。
上記証明の問題点など、お気づきの点がありましたらコメント等で教えていただければと思います。
よろしくお願いします。
おわりに$2$
・・・という締めの言葉を(2022.10.23に)書いてから約1日。
@minimalminami さんから嬉しいお知らせをいただきました!
@apu_yokai 上原先生にapuさんが昨日書いたレプ・キューブの不可能性のブログ記事を紹介したら、ちゃんと証明できてるって感心してました。コメントを残したかったけどやり方が分からなかったって言ってましたが。実はこの問題は一昨年くらいに上原先生も証明付けてたので興味深かったんだと思います。
— distinct slopes (@minimalminami) October 24, 2022
なんとなんと、本の著者である上原教授がこの記事を見ていただいた上、証明できているとおっしゃっていたとのこと!
これは嬉しいです~
そして、既に証明されていたとのこと。やはり「未解決問題を初めて解く」というのはなかなか経験できないものですね。
とはいえ、これほど感動的な体験はなかなかできないことだと思います。
みなさんも是非未解決問題にチャレンジしてみよう!
おわりに$3$ 未解決問題のその後の進展
「おわりに$2$」を書いた後、直接上原教授にメールして、返信をいただきました!
それでわかったのですが、今年 $3$ 月に出された論文に、上記の証明と同様の証明が出ているとのことでした。惜しかった(?)。
IEICE:Research on Dissections of a Net of a Cube into Nets of Cubes
(論文の閲覧は有料です)
それから、「$k=2,4,5,8,9,10,13,16,17,18,20,\ldots $といった二平方和となる数は正則なレプ・キューブが存在しそうな数である」の方の予想についても進展があったということで、既に $25$ 以下の数については全てレプ・キューブが見つかっていて、現在、解があるかどうかわかってない最小の $k$ は $26$ ということでした。
その他、「計算折り紙入門」で未解決問題として掲載されているもののうちいくつかは上記論文で解決されています。
「存在しそうな数」について解決済みのこと
最後の最後に、「存在しそうな数」について現在解決済みの主なものをご紹介します。
正則なレプ・キューブは無限に存在する
任意の正整数 $i$ に対して、次数 $k=18i^2$ の正則レプ・キューブを波型(w型)のポリオミノのみで構成できることからわかります。
なお、合同なポリオミノのみで構成されたレプ・キューブを「一様なレプ・キューブ」と呼びますので、
一様で正則なレプ・キューブは無限に存在する
ということも言えます。一方、
一様でない正則なレプ・キューブは無限に存在する
ということもわかっています。
「$6$つのパーツを点対称に組み合わせたもの × $6$ 枚」で次数 $36$ のレプ・キューブを構成できるので、任意の次数 $l$ のレプ・キューブの単位正方形を $k'^2$ 個 の小さい正方形に分割してから、同様のパターンに分割することで、次数 $36lk'^2$ の一様でない正則なレプ・キューブを構成することができます。
だいぶ長くなってしまいました。
いまのところ、未解決問題の中で一番手を出しやすそうなのは「次数 $26$ のレプ・キューブを構成する」あたりでしょうか。
より一般に「二平方和となる数を次数とするような正則なレプ・キューブが必ず存在する」ということまで証明できれば完全解決ですが、さて・・・
皆さんも是非挑戦してみてください!
