TMO2022に参加してみた

はじめに

この記事はOMC内で行われたTMO2022の参加記です.
頑張って書いたので読んで頂けると嬉しいです.
(10/31:少し追記しました. )

問題はこちらから → https://onlinemathcontest.com/contests/tmo2022

結果

ABCDEFGHJの9完(32位)でした.
全完いけるかもと思いましたがやっぱりきつかったですね.
あとペナが結構出てしまいました.
解いた順番はB→C→E→F→J→D→H→G→Aです.

問題ごとの解説(解けたやつ)

B

よくある確率漸化式の問題です.
人$n$が○な確率を$a_n$, ×な確率を$b_n$とすれば
$$a_n+b_n=1,　a_n=\frac{9}{10}a_{n-1}+\frac{1}{10}b_{n-1}$$
が成り立つので, これを解いて$a_n=\dfrac{1}{2}+\dfrac{1}{2}\Big(\dfrac{4}{5}\Big)^n$ が分かります. あとは適当に$\log$を使うと解けます.

〈こめんと〉多分これが最易ですかね？$0.8^n$の大小評価のところは電卓でもいけて$\log$使わなくてもできるので, かなり易しめだと思っています. ちなみに私は計算合わなかったのでローラーしました

C

これ好きです.
$N=a_M10^{M-1}+a_{M-1}10^{M-2}+\cdots+a_210^1+a_110^0$ とすれば
$f(N)+1=(a_1+1)(a_2+1)\cdots(a_{M-1}+1)(a_M+1)$ です.
ここで, ちょっと実験してみましょう.
$N=1111→f(N)=15$　×
$N=10000→f(N)=1$　×
$N=12345→f(N)=719$　×
$N=9999→f(N)=9999$　○
なんか$N$の方が大きそうです.
といってもよく考えると当たり前っぽくて, 最後に数字を付け足す($123→1234$みたいな感じです)と$N$は約$10$倍されるのに比べて$f(N)$は$a_{1}+1$倍しかされません. 特に各桁の数字はほとんど$9$であって欲しいです.
これをちゃんと表してみます.
$N=10a+b ~ (0 \leq b \leq 9)$とおいたとき, $f(N)=f(a)(b+1)+b$が成り立ちます .
もし$f(a)=a$かつ$f(N)=N$だとすれば$b=9$で, $0 \leq b \leq 8$なら$f(N)\leq N$になってしまいます.
これを繰り返すことで最初の数字以外は全て$9$が必要十分なことが分かりました. あとは最初の数字で場合分けをすると解けます.

〈こめんと〉楽しいです. 楽しいです. 上のような感じで 感覚→軽く証明 をしておくとミスをしにくくなります.

E

五心が絡む幾何の問題です.
$BCI_A$の外心というのは難しそうですが, 下の定理を思い出します.

これより$A,B,C,O$は同一円周上にあります.
また, 傍心は扱いにくいので内心$I$をとります. さらにもう一度定理1を使うことで$AI_A:OI_A=8:3$は$AI:IO=2:3$と同値だと分かります. これでもう$I_A$は消してもいいです.
ここからはどうやってもできると思います(多分). 私の解法を書きます.

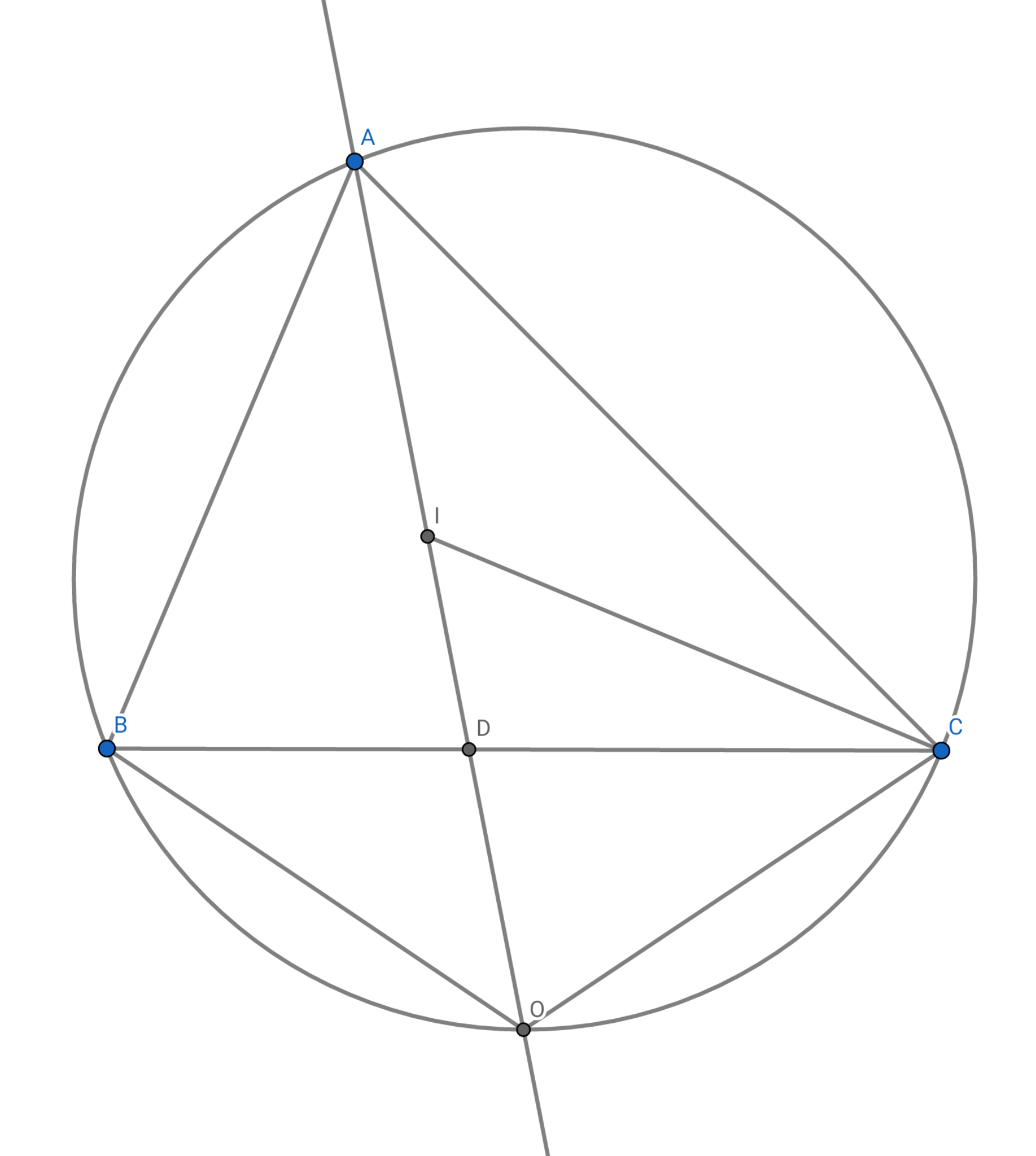図1
角$A$の二等分線と辺$BC$の交点を$D$とします.
$BD:DC=AB:AC=4:5$なので$BD=4x, ~ DC=5x$とおきます.
また, $AI=2y, ~ IO=3y$とおきます. (いろんな線分の長さを$x,y$で表して方程式を立てることを目標にします. )
定理1より$OB=3y$で, 三角形$BOD$と$ACD$の相似より$BO:OD=AC:CD$が成り立つので, $OD=3xy$が分かります.
また, $AI:ID=AC:CD=1:x$なので, $ID=2xy$です. これより$IO=5xy$です.
ここで, $IO=3y$だったので$3y=5xy$, つまり$x=\dfrac{3}{5}$です.
以上より, $BC=9x=\dfrac{27}{5}$です.

〈こめんと〉トリリウムの定理はよく出るので覚えておきましょう. 自分の解法についてなんですが, $3y=5xy$が出てきたのはかなり驚きました. 割と綺麗な解法になっていると思います.

F

これ難しいと思います. 一旦実験してみましょう.
例えば, $(1,3,5,7,2,4,6)$にこの操作を繰り返すと
$$(1,3,5,7,2,4,6)→(1,5,2,6,3,7,4)→(1,3,5,7,2,4,6)→ \cdots$$になります.
どうやらサイクルが大事っぽいのでグラフを書きます.
(サイクルというのは大雑把に言うと図2でいう輪っかです. )

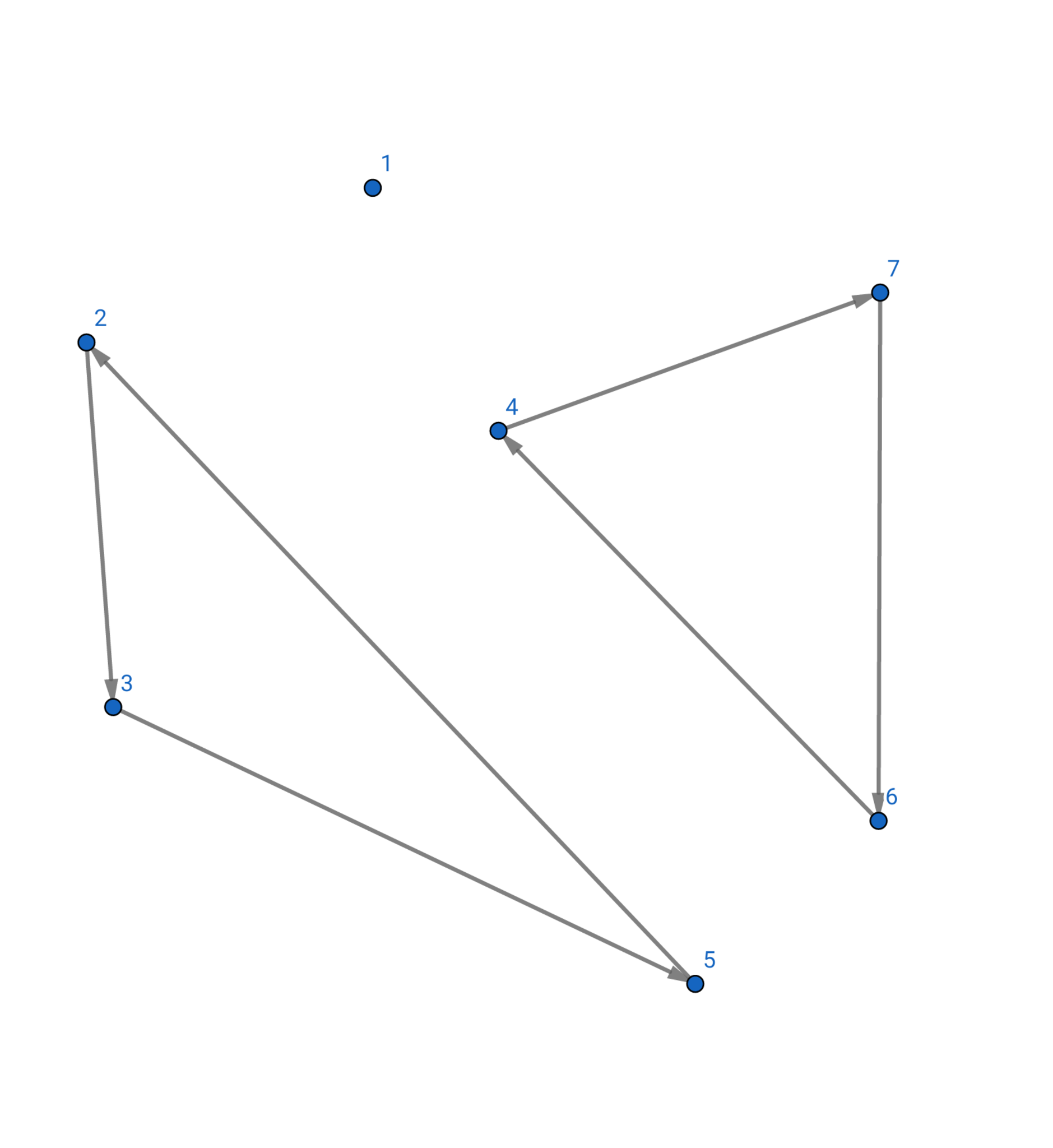図2
いくつか進んでいることは確かなので, 問題はいくつ進んでいるかです.
(以下では, 見にくいので$P_i$を$f(i)$と表します. )
操作は$f(i)$を$f(f(i))$に変えるものでした.
$1$回目　$f(i)→f(f(i))$
$2$回目　$f(f(i))→f(f(f(f(i))))$ ($ff$を一つの並び替えと見ます. )
$\cdots$
$k$回目　$f^{2^{k-1}}(i)→f^{2^{k}}(i)$
$k+1$回目　$f^{2^{k}}(i)→f^{2^{k+1}}(i)$
条件は｢$i=1,2,\ldots,7$について$f^{2^{k}}(i)=f^{2^{k+1}}(i)$なる$k$が存在する｣です. $f^{2^{k}}(i)=f^{2^{k+1}}(i)$は$f^{2^{k}}(i)=i$と同値なので
$f^{2^{k}}(i)=i$なる$k$が存在すれば良いです.
グラフの議論に戻ります. $2^k$進んで元に戻るということなので, サイクルの長さは$2^k$の約数, つまり, サイクルの長さは$2$べきだと分かります(これは必要十分条件です). よって, $7$を$2$べきに分ければ良いです. 分け方は次の$6$通りあります.
$(1) ~ 4+2+1$
$(2) ~ 4+1+1+1$
$(3) ~ 2+2+2+1$
$(4) ~ 2+2+1+1+1$
$(5) ~ 2+1+1+1+1+1$
$(6) ~ 1+1+1+1+1+1+1$
ここで, 長さが$4$のサイクルに矢印をつける方法は$(4-1)!=6$通りあります. (円順列の方法の数です. )
これに注意すればそれぞれの方法の数は
$(1) ~ ({}_7 C_4×6)×3=630$
$(2) ~ {}_7 C_4×6=210$
$(3) ~ 7×({}_6 C_2×{}_4 C_2÷3!)=105$
$(4) ~ {}_7 C_3×({}_4 C_2÷2!)=105$
$(5) ~ {}_7 C_2=21$
$(6) ~ 1$
なので, これらを全て足して答えを得ます.

〈こめんと〉手数が多めで難しいです. ちなみに私は${}_7 C_2=35$として$2$ペナしました. 計算ミス, こわいです.

J

ごめんなさい, エスパーしました.
$f(0)=n$ とおいておきます.
$x$と$y$に$0$を代入すると$f(n)=\alpha(n+2)+2022$を得ます.
また, $x$のみ$0$を代入すると$f(f(y))=\alpha(n+2)+4y+2022$を得ます.
これより, $f(f(y))=4y+f(n)$なので, $f(x)$は$2x+c$または$-2x+c$と予想できます. (あくまでも予想です. )
これを元の式に代入すると, $\alpha-1$が$2022$の約数なことが分かるので, この総和を求めれば良いです.

〈こめんと〉公式解説見たら思ったより難しそうでびっくりしました. 関数方程式の問題, 昔作って没になったことがあるのでまた作りたいです.

D

これ難しくないですか？
$A,B,C,D$の球の個数を$a,b,c,d$とします. 条件は$a+b+c+d=100$かつ$a \gt b,c,d$です.
ここで, $(a-b-1)+(a-c-1)+(a-d-1)=4a-103$と式変形ができます. $a-b-1,a-c-1,a-d-1$は正で, $a$より小さいので, 包除原理を使うことを考えます.
このうち1つ以上が$a$以上なもの, このうち2つ以上が$a$以上なものの個数を求めて, 計算すれば解けます. (めんどくさいので雑です. すみません. )

〈こめんと〉筋肉。体育会系数学部です.

H

実は見た目より簡単です.
赤玉の間にある青玉の個数だけ数えればいいので和が$6$の$6$つの数を円に並べるのと一緒になります.
$360°$回転させて初めて重なるものは, 回転を区別させて並べたものの個数の$\dfrac{1}{6}$です.
$180°$回転させて初めて重なるものは, 回転を区別させて並べたものの個数の$\dfrac{1}{3}$です.
$120°$回転させて初めて重なるものは, 回転を区別させて並べたものの個数の$\dfrac{1}{2}$です.
$60°$回転させて初めて重なるものは, 回転を区別させて並べたものの個数の$\dfrac{1}{1}$です.
それぞれ, 回転を区別させて並べたものの個数は${}_6 H_6=462, {}_3 H_3=10, 3,1$(演習:なぜですか？)なので, 重複に気をつけて, 答えは
$$\dfrac{462-(10-1)-(3-1)-1}{6}+\dfrac{10-1}{3}+\dfrac{3-1}{2}+1=80$$
になります.

〈こめんと〉ごめんなさい. 説明をサボりました. これは自分でもよくわかっていませんが, 回転を区別しない問題は｢初めて重なる角度｣で場合分けするといいと思います.

G

見た目がゴツいです.

以上です.

〈こめんと〉$mod 42$周期なのはフェルマーの小定理を思い出すと気付きやすいと思います. 剰余の問題, ほとんどが計算重いのできついです.

A

$254×5598$です. 以上です.

〈こめんと〉公式解説が手を抜いていますね. でも本当にこれ以上書くことがないと思います.

問題ごとの感想(解けなかったやつ)

I

図を書いて解いてみたら全然解けなくて焦りました. 解説のめっちゃ難しい解説を見て安心しています. 極線, 全く勉強してないのでわからないですね.
座標に走ればよかったと少し後悔しています.
　　　　 　　　　　　　　　　　　F > I って本当ですか

K

計算が重そうということだけ分かりました.

L

図すら書いてません. 諦めモードです.

おわりに

後半かなり手を抜きました. ごめんなさい.
これからまた別の記事を投稿するかは分かりませんが, 気が向いたらどんどん書いていきたいですね.

最後に, ここまで読んで頂きありがとうございました.