反転を知らない人のためのトレミーの定理の証明方法

はじめに

トレミーの定理

円$\Gamma$上の(凸)四角形$ABCD$について、
$$AB \cdot CD + BC \cdot DA = AC \cdot BD$$

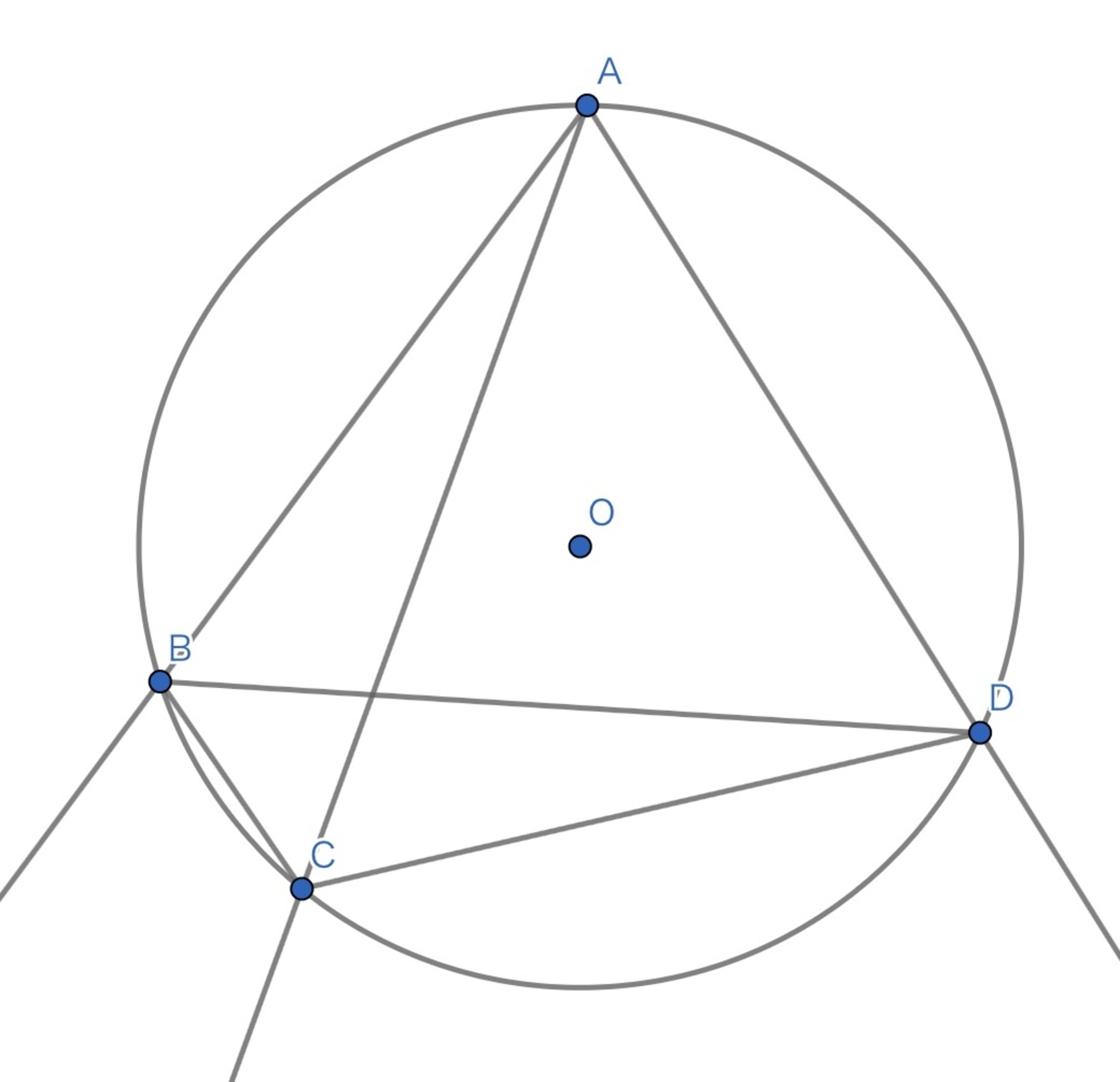トレミーの定理

トレミーの定理の証明は、反転以外認められないということが広く知られています。
では、反転を知らない人はトレミーの定理を未証明で使うしかないのでしょうか？
もちろんそんなことはありません！

証明

補助線を引く

直線$AO$と$\Gamma$の交点$P$($\neq A$)をとります。
半直線$AB$,$AC$,$AD$を引き、$P$における$\Gamma$の接線$s$との交点をそれぞれ$B^\prime,C^\prime,D^\prime$とします。
さらに、$\Gamma$の直径の長さ($=AP$)を$r$とおきます。

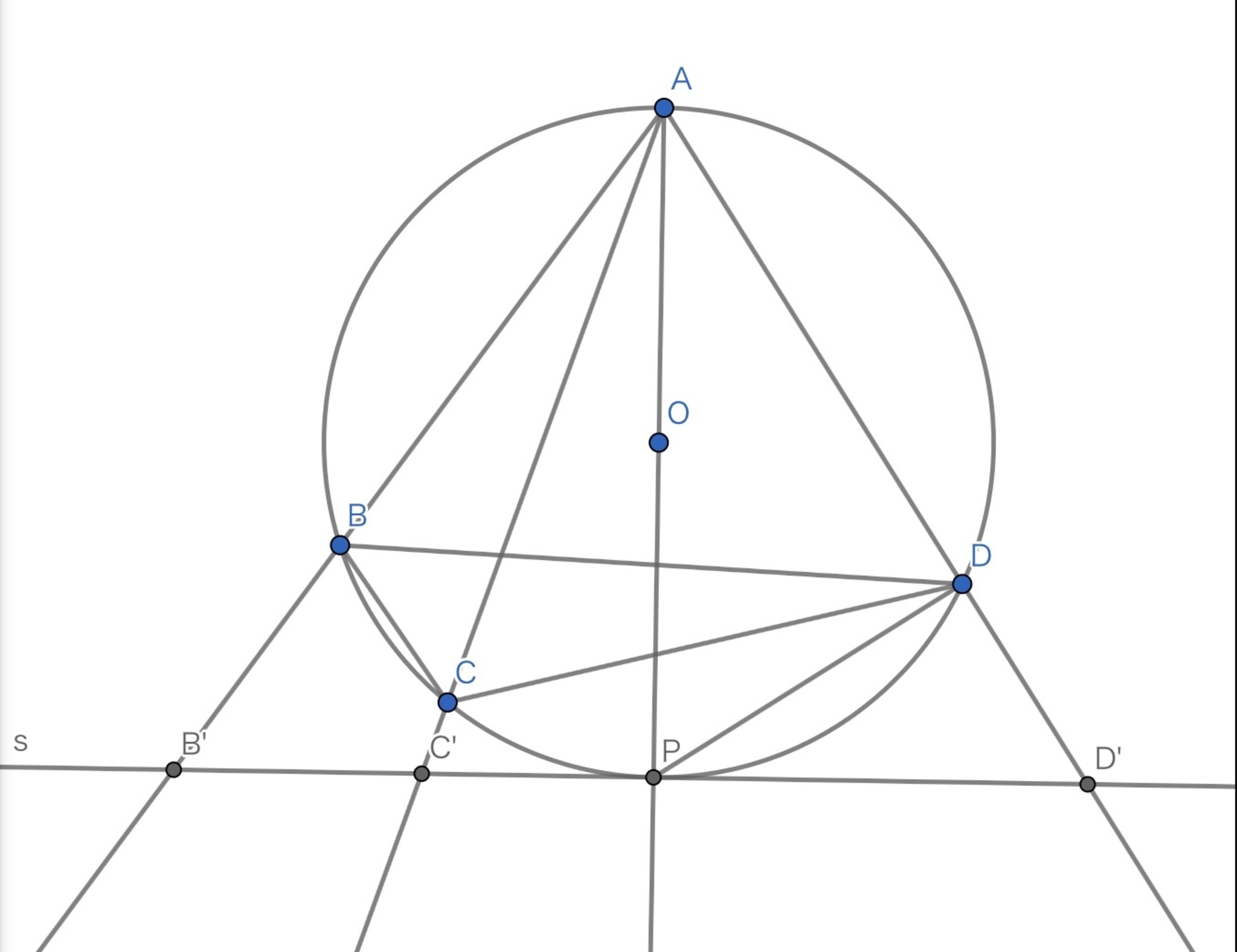補助線

長さの変換

$AB,AC,AD$

対称性より、$AD$のみ考えればよいです。
方べきの定理の証明を使います。

線分$AP$は$\Gamma$の直径なので、$\angle ADP = 90^\circ = \angle APD^\prime$で、$\angle PAD = \angle D^\prime AP$から
$\triangle ADP \backsim \triangle APD^\prime$が従います。

よって、$AD : AP = AP : AD^\prime,$ $AD \cdot AD^\prime = r^2$で、変形すると$AD = \dfrac{r^2}{AD^\prime}$です。

$AB,AC$についても同様なので、

です。

$BC,CD,BD$

こちらも、$BC$のみ考えます。
$AB \cdot AB^\prime = r^2 = AC \cdot AC^\prime$より、$B,C,C^\prime,B^\prime$は共円で、
さらに$\triangle ABC \backsim \triangle AC^\prime B^\prime$です。
よって、$BC : C^\prime B^\prime = AB : AC^\prime$で、整理すると$BC = C^\prime B^\prime \cdot \dfrac{AB}{AC^\prime}$が得られます。
$AB$も補題3で変換してしまうと、$BC = C^\prime B^\prime \cdot \dfrac{r^2}{AB^\prime \cdot AC^\prime}$です。

$CD,BD$についても同様なので、

です。

主張の変換

$AB \cdot CD + BC \cdot DA = AC \cdot BD$に補題3,補題4を適用すると、

です。(途切れている場合は横にスクロール)
両辺を$\dfrac{r^4}{AB^\prime \cdot AC^\prime \cdot AD^\prime}$で割ります。

$ABCD$の凸性より、$B^\prime,C^\prime,D^\prime$はこの順に並んでいるので、$D^\prime C^\prime + B^\prime C^\prime = D^\prime B^\prime$は成立します。(向きは合ってないですが、有向長ではないので大丈夫です。)
これでトレミーの定理が証明されました！

補足

この証明は、明示的に反転が登場するわけではありませんが、やっていることは反転です。
補助線についても、反転を知らなければ相当天下り的に見えそうですが、結局反転です。
また、これは反転なので、トレミーの定理の証明として適切です。
(反転を知らない方は、Googleで「反転幾何」と検索してみましょう。)