消えた正方形の謎を追え (Missing square puzzle)

本稿では，Missing square puzzleと呼ばれる錯視において，正方形の穴が生じる理由を解説する．

Missing square puzzleとは？

まずは，以下に示す2つの図形を見ていただきたい．
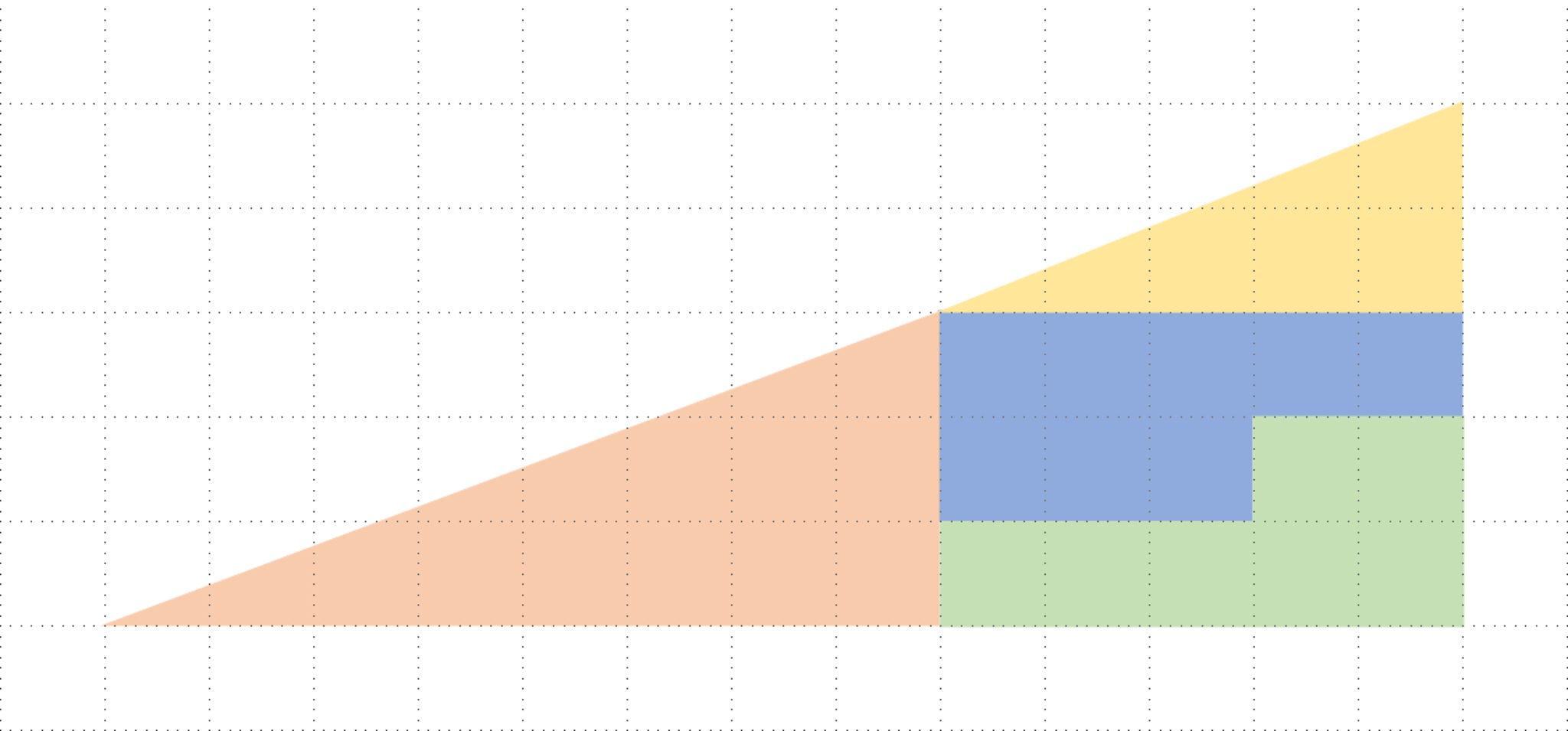Missing square puzzle（正方形が欠けていない状態）
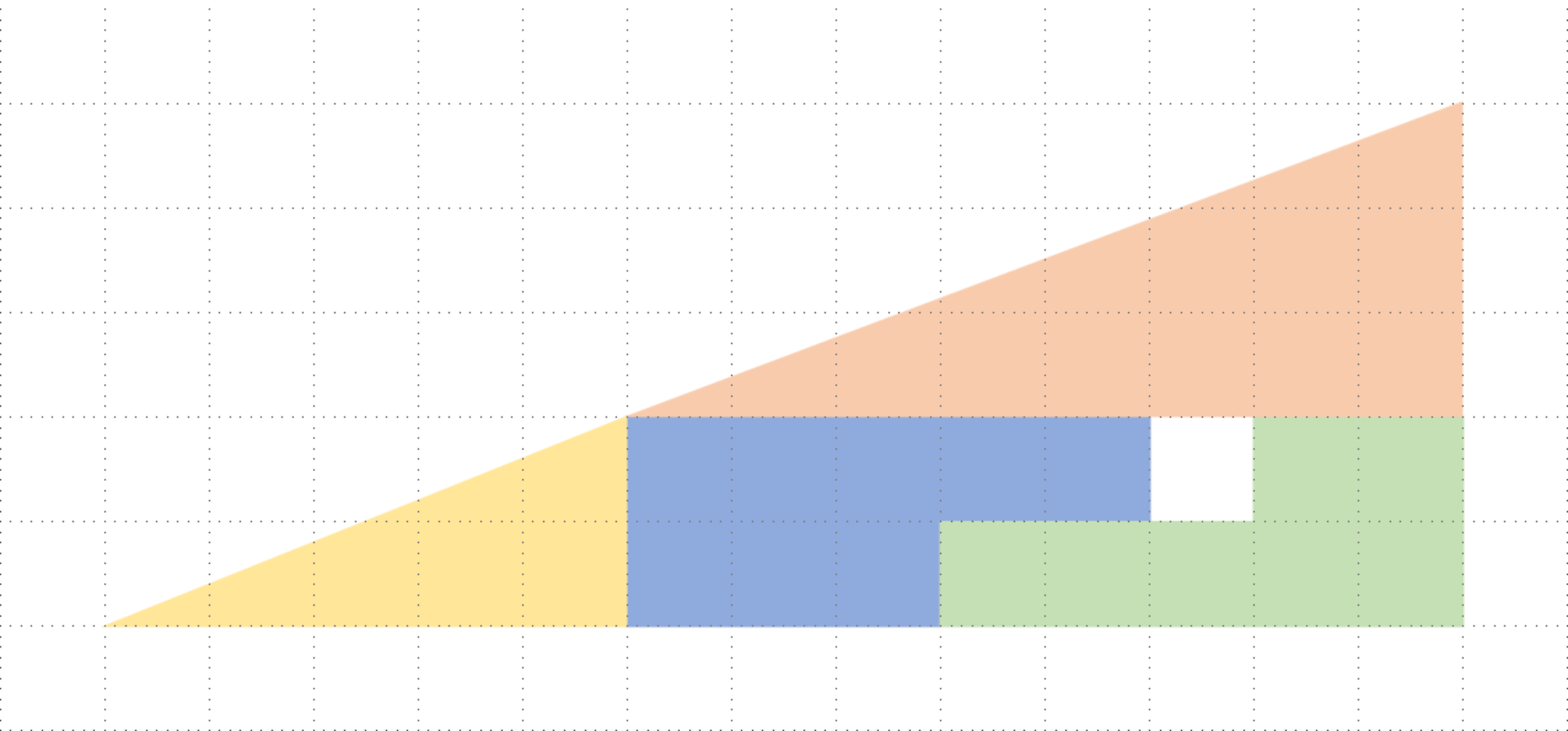Missing square puzzle（正方形が欠けている状態）
なんということでしょう．
図1も図2も，4種類の同じ多角形で同じ図形を形作っているはずなのに，図2には正方形の穴ができているではありませんか．

これが，Missing square puzzleである．
本稿の目的は，Missing square puzzleで何が起こっているのかを説明することである．

図形をよく見てみると……？

先ほどの図1と図2に，一本の補助線を引いてみよう．
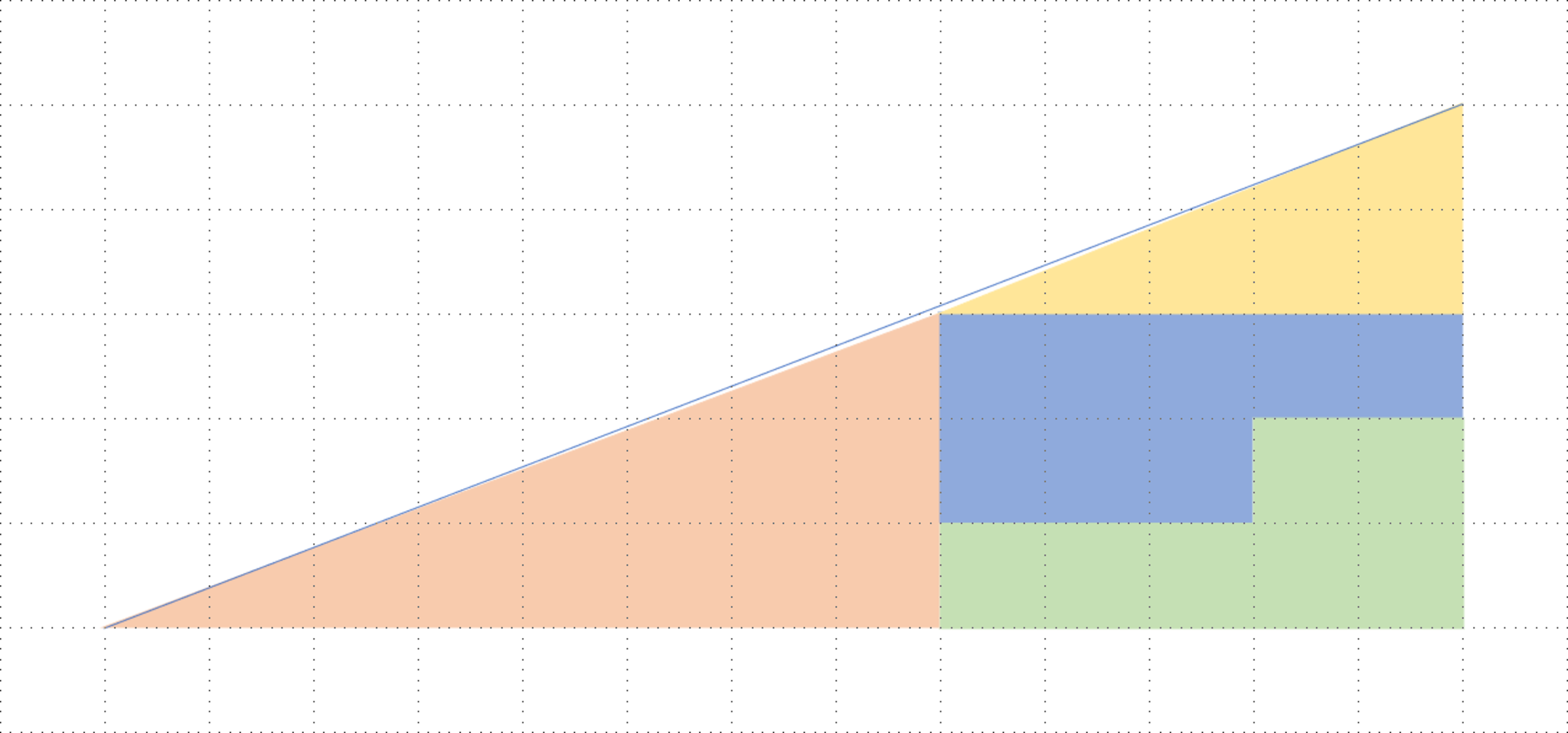図1に補助線を引いたもの
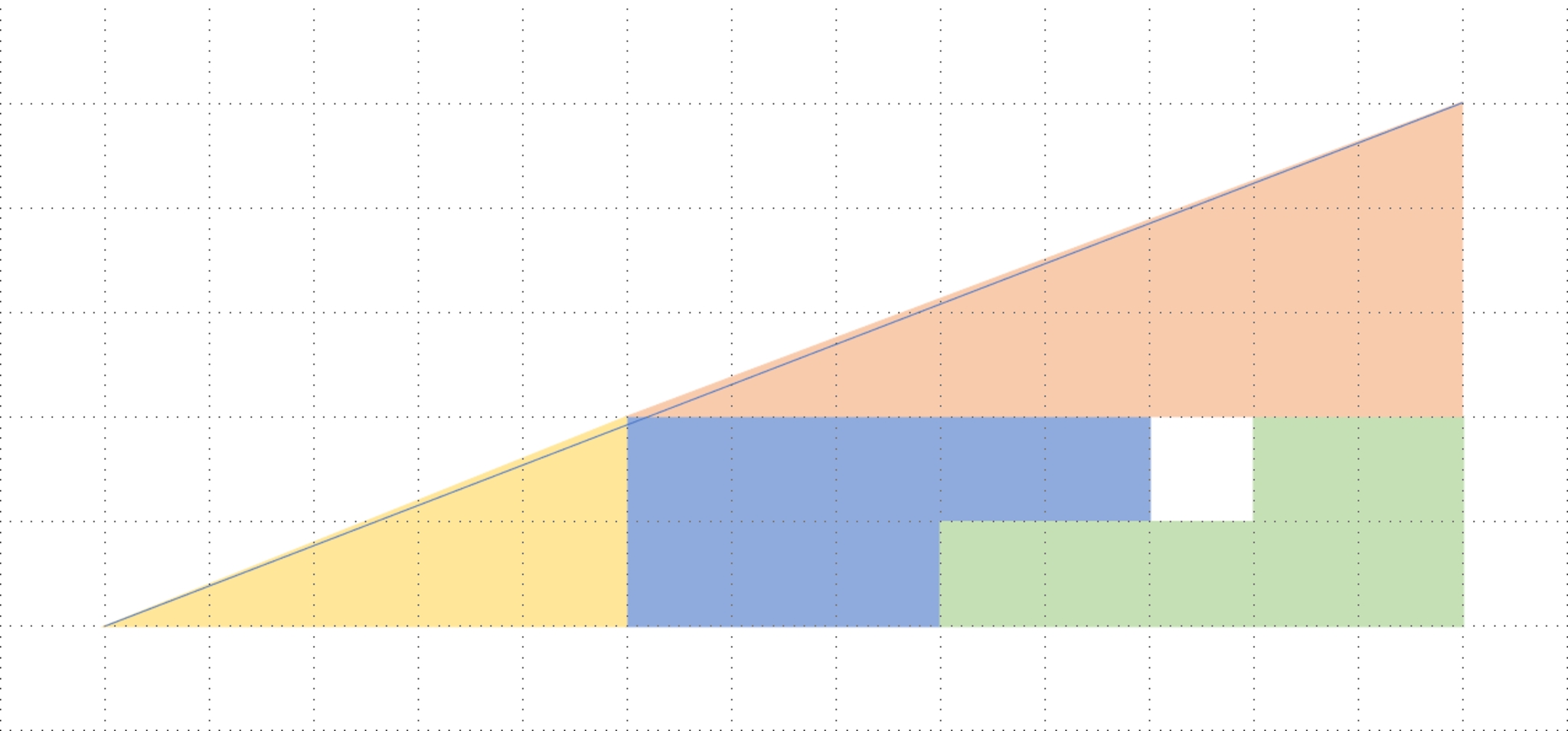図2に補助線を引いたもの
ん？
なんか斜辺ずれてね？

そう，4つの多角形が形作っていた図形は，直角三角形ではなかったのだ．図1では凹四角形，図2では凸四角形が形作られている．それをわかりやすくしたものが，以下に示す図である．
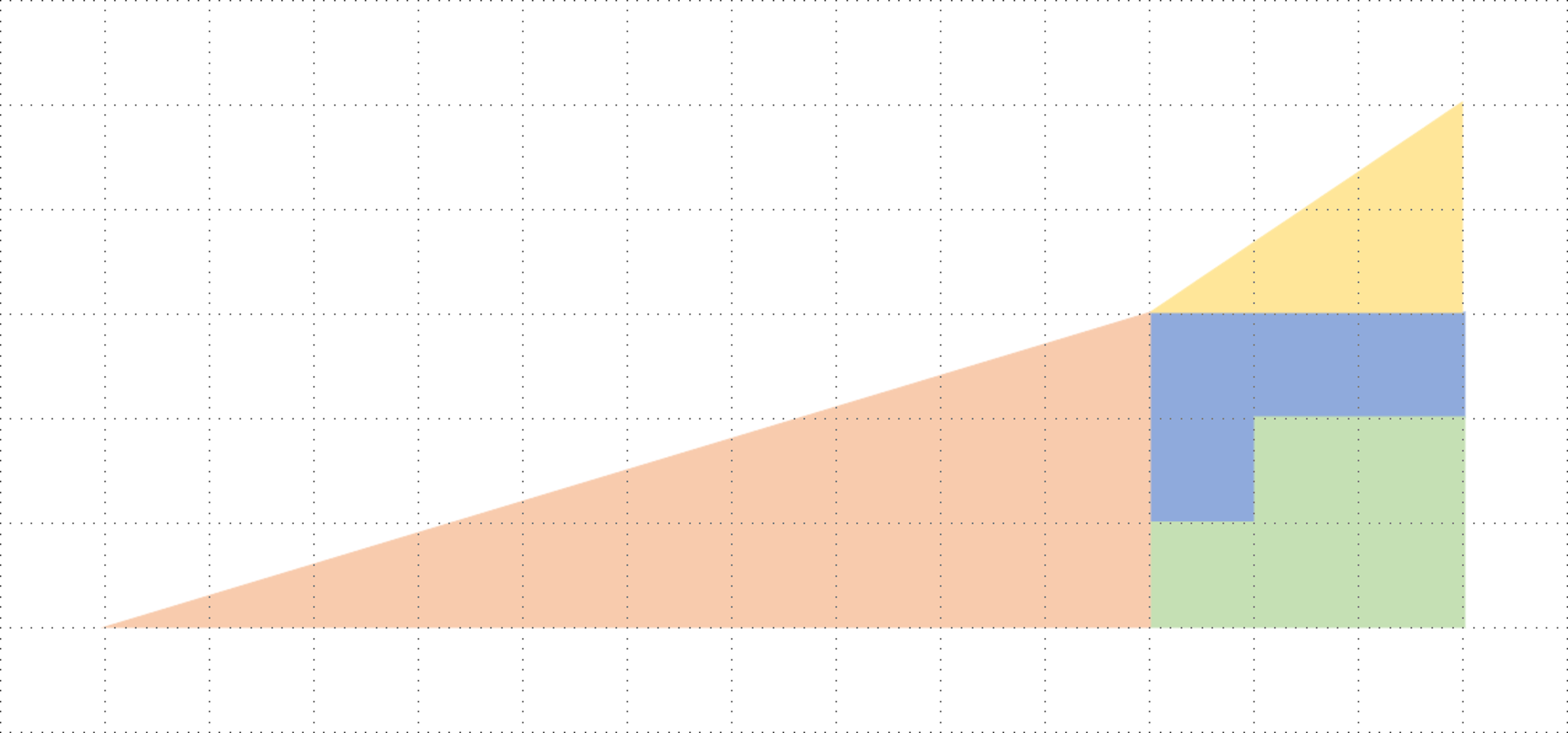図1が“凹四角形”であることを露骨に表現したもの
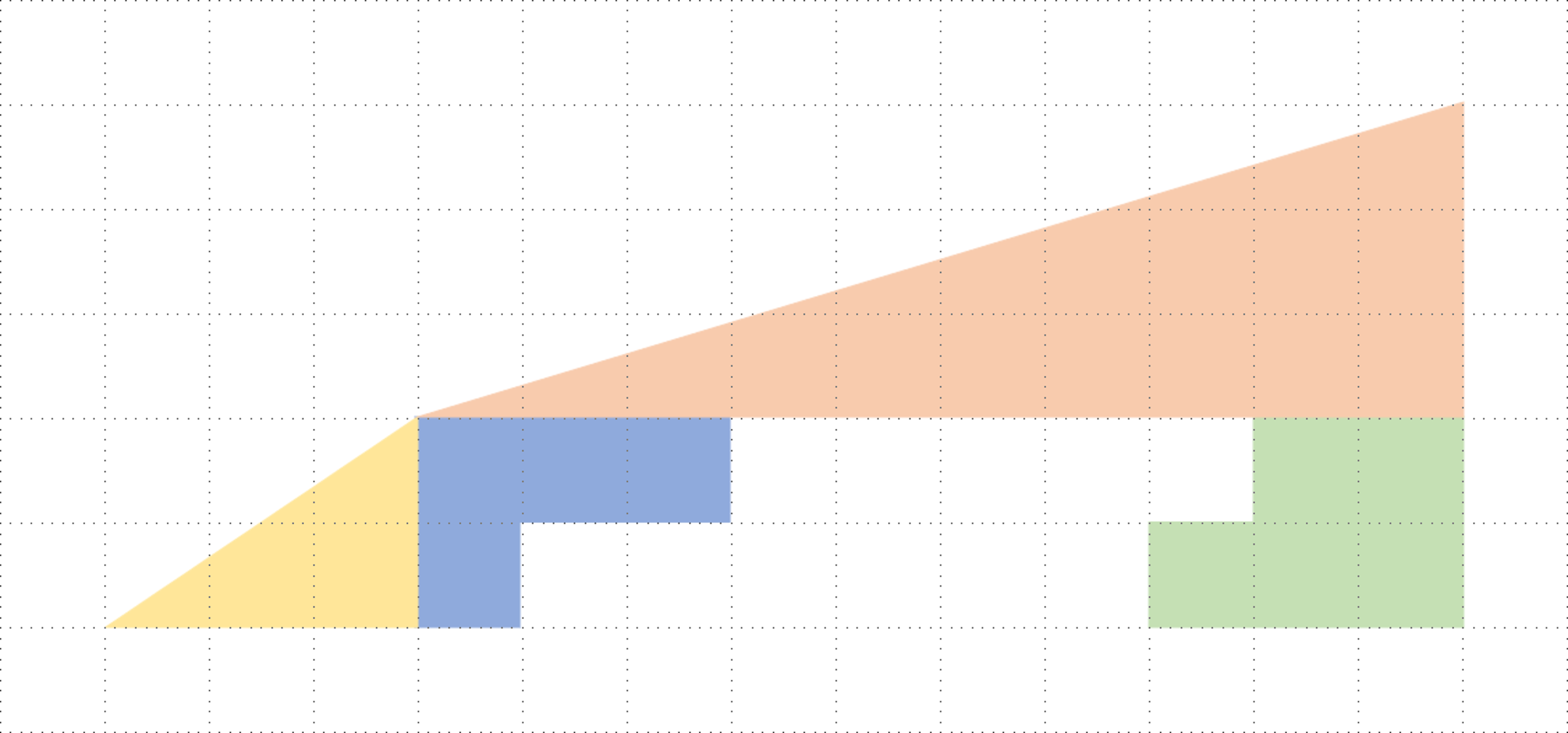図2が“凸四角形”であることを露骨に表現したもの
図5と図6では，4つの多角形が図1と図2とは異なっていることに注意されたい．図6では，斜辺の「歪み」が露骨になった分，図2に比べて「欠け」が大きくなっている．

このように，Missing square puzzleは，直角三角形ではない図形が直角三角形に見えてしまう錯視である．

正方形の穴を「証明」する

図2では，大きさがちょうど1マス分の正方形の穴ができている．Missing square puzzleにおいてこのような現象が起こることを，きちんと説明してみよう．

歪みの面積を求める

図1と図2で用いられている4つの多角形の面積の和は，
$$ (橙の直角三角形)+(黄の直角三角形)+(図1で青と緑の図形がなす長方形) =\frac{1}{2}\cdot8\cdot3+\frac{1}{2}\cdot5\cdot2+3\cdot5 =32 $$
である．一方，図1と図2で我々の目に「見え」てしまっている直角三角形の面積は，
$$ \frac{1}{2}\cdot13\cdot5=32.5 $$
である．よって，図3において「補助線」「橙の直角三角形の斜辺」「黄の直角三角形の斜辺」がなす三角形の面積は
$$ 32.5-32=0.5 $$
となる．
また，図3で引いた補助線と図4で引いた補助線は同一であるから，図4において「補助線」「橙の直角三角形の斜辺」「黄の直角三角形の斜辺」がなす三角形の面積も$0.5$である．

歪みが生み出す差を求める

図3では直角三角形の斜辺にあたる部分が凹み，逆に図4では出っ張っていることから，図1と図2の図形の面積の差は，歪み2つ分，すなわち$2\cdot0.5=1$である．これが，図2で生じている正方形の穴の正体である．

演習課題

1. 次の図7について，以下の(1)，(2)の問いに答えよ．
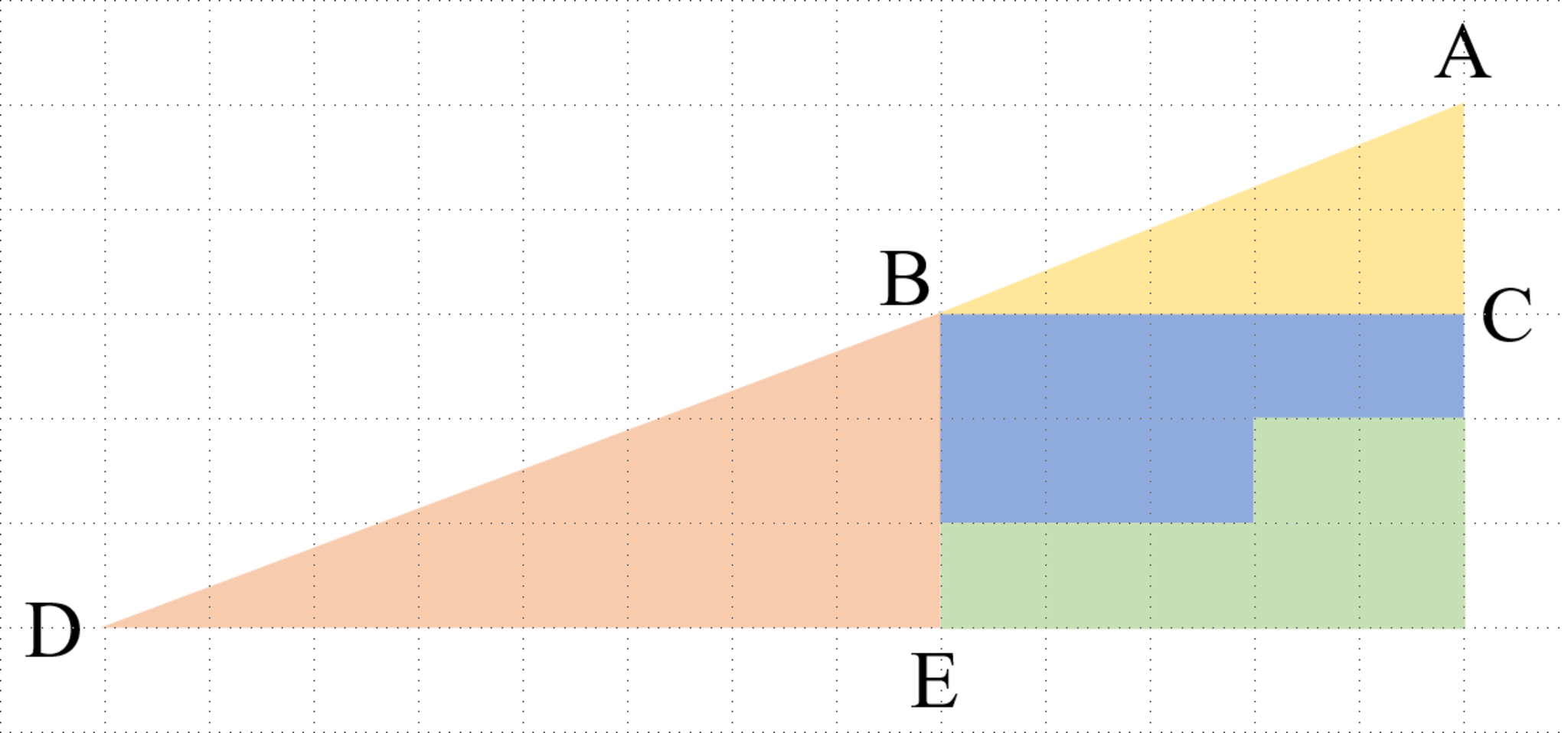   図1と同じものである
   1. $\angle\mathrm{ABC}$と$\angle\mathrm{BDE}$とではどちらが大きいか．
   2. (1)において，大きい方を$\alpha$，もう一方を$\beta$とするとき，$\alpha-\beta$のおよその値を求めよ．ただし，$|\theta|$が$1$と比べて十分小さいとき$\tan\theta\fallingdotseq\theta$であることを用いてもよい．
2. 3辺の長さが$\sqrt{29}, \sqrt{73}, \sqrt{194}$である三角形の面積はいくつか．
3. Chessboard paradoxについて調べ，本稿と同様に考察せよ．