競技数学解説

文献あり

USAMO 2003 4 を解く

初等幾何

111

この記事はあくまでも個人のメモとして利用しています．賢い解法などは載っておりませんのでご了承ください．

自己紹介(？)

　僕はただの数弱なので自己紹介は恥ずかしいです．なので遠慮させて頂きます．

USAMOを数弱が解いてみた。

USAMO 2003 4 問題文簡略化

以下の図 $1$ において
$M F = M C \Leftrightarrow M C^{2} = M D \cdot M B$ 　を示せ．

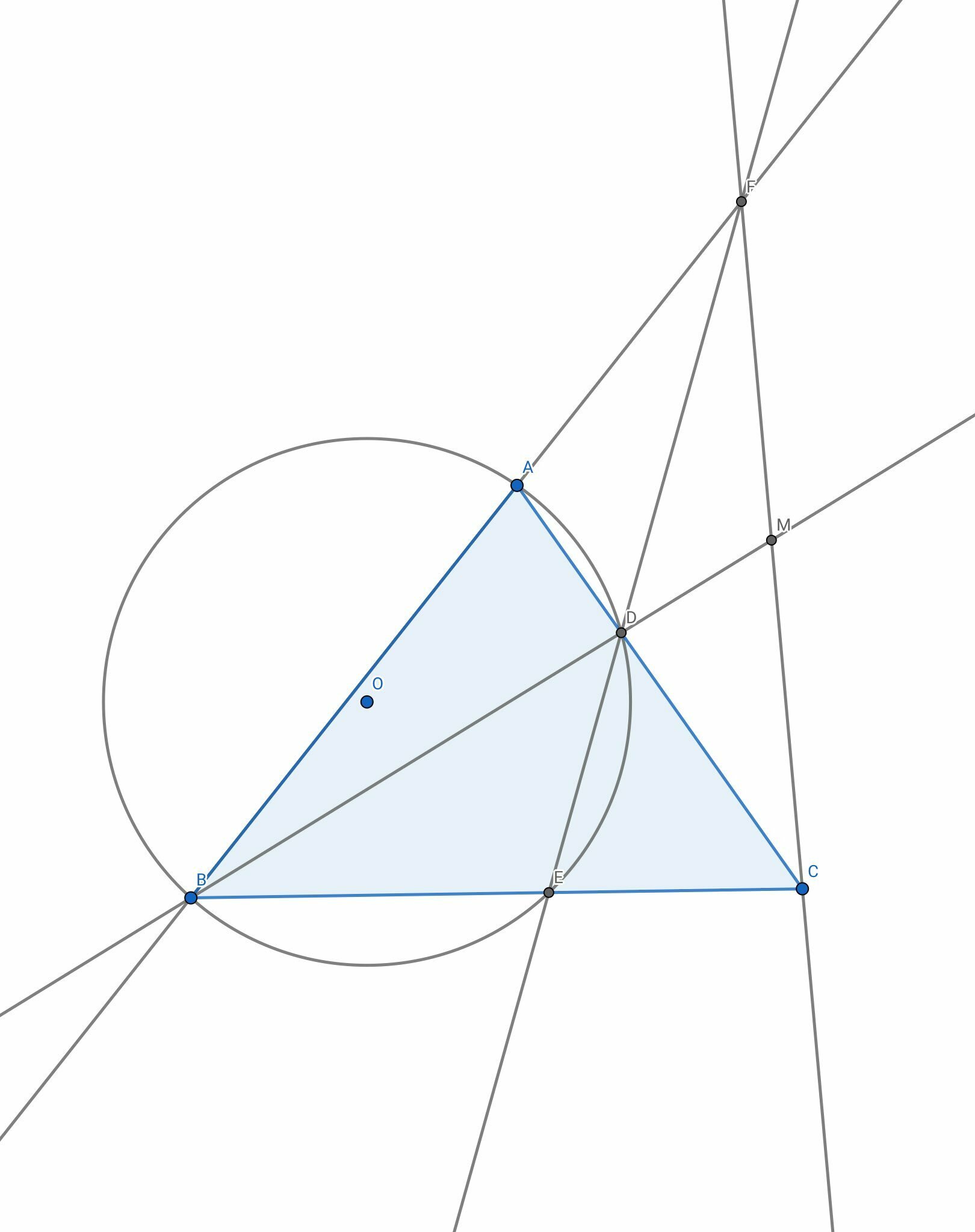問題の図形

　流石に問題の本文を載せておきます．(省略し過ぎた…)

原文

Let $A B C$ be a triangle. A circle passing through $A$ and $B$ intersects segments $A C$ and $B C$ at $D$ and $E$ , respectively. Lines $A B$ and $D E$ intersect at $F$ , while lines $B D$ and $C F$ intersect at $M$ . Prove that $M F = M C$ if and only if $M B \cdot M D = M C^{2}$ .

$M F = M C \Rightarrow M C^{2} = M D \cdot M B$

　なんか方冪チックな式が出てきましたね．なかなか手強い見た目してます(？)．直接 $M C^{2} = M D \cdot M B$ を示すのはなかなか面倒臭いので，方冪の定理を利用するであろうという希望的観測の元，条件の言い換えを行なっていきます．
$M C^{2} = M D \cdot M B \Leftrightarrow 直線 M C は △ B C D の外接円と接する．$
ってことで，外接円に直線が接することを示します．
　とは言っても，しばらく手が止まってしまいました．分からない，どうしよう，そう悩んでいるといつの間にか $20$ 分経過していました〜(泣)．
　ここで再び図形を眺めてみると，何かに気づきました．
　あ， $C e v a$ の定理だ！！いけるぞ！！
　(いい加減，真面目に書きます．)

　まず，以下の予想を示す．

$A E ∥ F C$

予想の証明

C e v a

の定理から

\begin{array}{rcl} \frac{F A}{A B} \cdot \frac{B E}{E C} \cdot \frac{C M}{M F} & = & 1 \\ \Leftrightarrow \frac{A B}{A F} & = & \frac{B E}{E C} \end{array}

上の式より，

△ BAE \sim △ BFC

が分かる．これら

2

つの三角形は正の相似となるので，

A D ∥ F C

　次の順序に従って示す．

$∡ DBC = ∡ DCM$

証明

円周角の定理から

∡ DBC = ∡ DAE

ここで予想から

∡ DBC = ∡ DAE = ∡ DCM

直線 $F C$ は $△ BCD$ の外接円に接する．

証明

∡ DBC = ∡ DCM

よりすぐ分かる．

$M C^{2} = M D \cdot M B$

証明

方冪の定理より分かる．

$M D \cdot M B = M C^{2} \Rightarrow M F = M C$

　先程同様，方冪の定理が重要になると思い，すぐに回答を出すことができました．

(iPadでの編集は疲れるのでだいぶ省略します．ご了承ください．)

$△ BCD$ の外接円と直線 $B C$ は接する．

証明

方冪の定理の逆より分かる．

$△ BDF$ の外接円と直線 $F C$ は接する．

証明

A n g l e C h a s e

を繰り返して

∡ ABD = 90^{\circ} - ∡ MBC - ∡ CFE - ∡ EFB = 90^{\circ} - ∡ CFB - ∡ ACF = 90^{\circ} - ∡ CBA = 90^{\circ} - ∡ FEC = ∡ CFE

より分かる．

$M F = M C$

証明

方冪の定理を用いて

M F^{2} = M D \cdot M B = M C^{2}

より分かる．

最後に

　初めてこのサイトに入力してみたのですが，だいぶ疲れてしまいました(笑)．次(いつになるかはわわからないですが…)はもっと時間をかけてクオリティを上げていきたいと思います♪

(最後に外接円を書き込んだ図を置いておきます．)

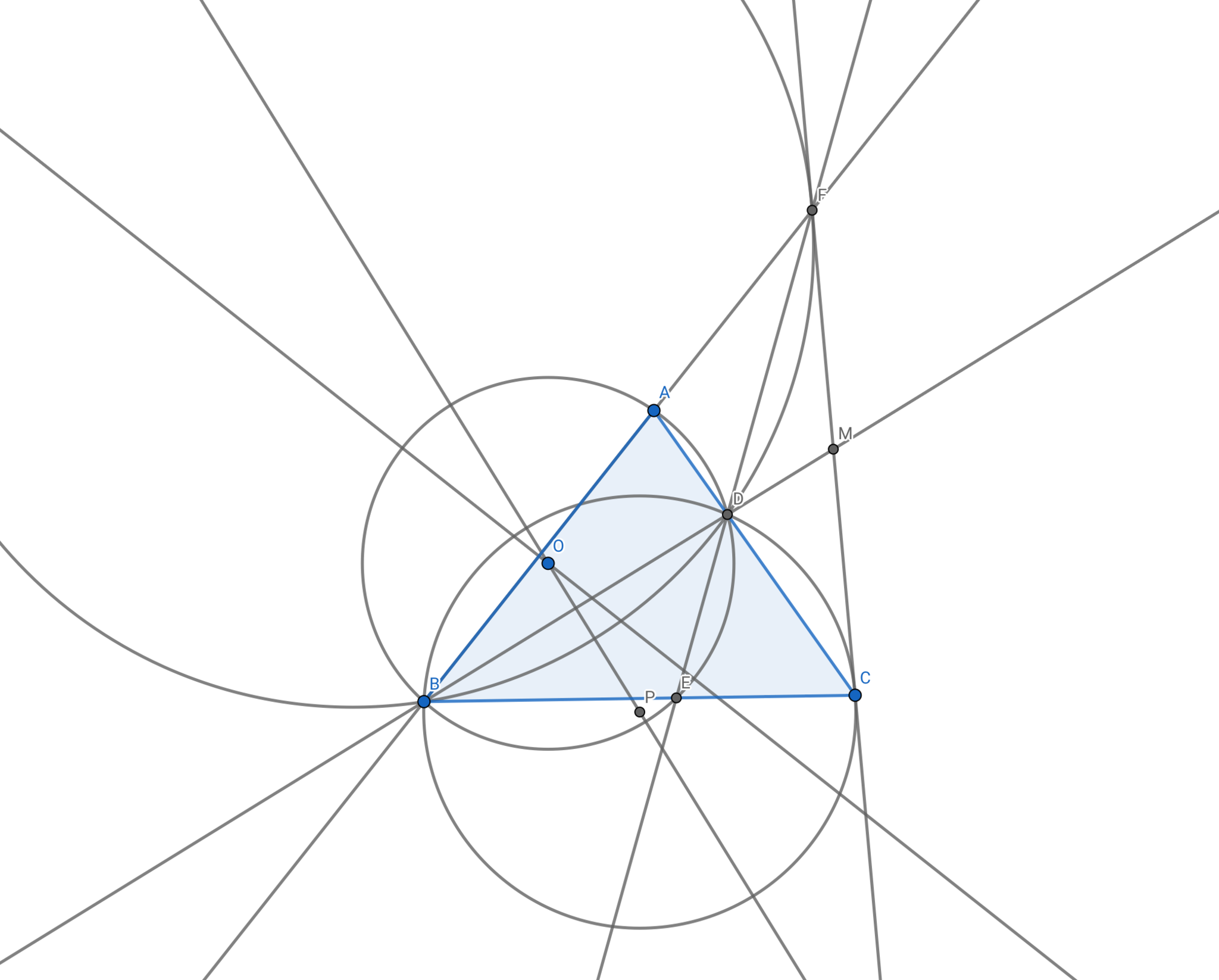外接円ありバージョン

参考文献

[1]

AoPS, 閲覧日 2022年12月7日, https://artofproblemsolving.com/community/c4501_2003_usamo

投稿日：2022年12月7日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

pqr_mgh

3429

他の人のコメント

コメントはありません。

読み込み中

pqr_mgh

USAMO 2003 4 を解く

自己紹介(？)
USAMOを数弱が解いてみた。
$MF =MC \Rightarrow MC^2 = MD \cdot MB$
$MD \cdot MB = MC^2 \Rightarrow MF=MC$
最後に
参考文献

USAMO 2003 4 を解く

自己紹介(？)

USAMOを数弱が解いてみた。

MF=MC⇒MC2=MD⋅MB

MD⋅MB=MC2⇒MF=MC

最後に

参考文献

この記事を高評価した人

この記事に送られたバッジ

投稿者

コメント

他の人のコメント

$M F = M C \Rightarrow M C^{2} = M D \cdot M B$

$M D \cdot M B = M C^{2} \Rightarrow M F = M C$