エンタメ解説

文献あり

ジャグリングの数理

ジャグリング,Juggling,サイトスワップ

732

はじめに

この記事は物工/計数 Advent Calendar 2022 の14日目の記事です。

この記事では、私の趣味であるジャグリングと数学の関係について説明してみようと思います。

一応Mathlog内にジャグリングと数学の関連性について語った記事がないか確認しましたが0件でした(「juggling」で検索しても0件)。

「ジャグリング」の検索結果ということはこれがMathlog初のジャグリングについて語った記事なわけですね。

「ジャグリングと数学って全く関係ないのでは？」と思った方も多いかもしれませんが、ジャグリングの技を有限非負整数列で表現する「サイトスワップ」なる概念は非常に重要で、ジャグリング界隈に広く普及しています。

こういった記事を書くのは初めてなので、嘘をいっぱい書いているかもしれません。そのときは教えてください。また、分かりやすく書ける自信はないので、分かりにくい部分は適宜参考文献などを参照してください。

ジャグリングのモデル化

サイトスワップを導入するにあたって、ジャグリングに以下のような制約を課します。

ボールは左右交互に一定間隔で投げられる。
片手で複数のボールをキャッチ、投げることはない。

また、投げる物体は何でも良いのですが、ここではボールとして考えます。

ジャグリングダイヤグラム

1つ1つのボールの軌道を時間軸に沿って表したジャグリングダイヤグラムというものを考えてみます。例として、3ボールカスケード(最も基本的な技)のジャグリングダイヤグラムを描いてみましょう。

3ボールカスケードのジャグリングダイヤグラム

丸はボールを投げるタイミング、その下には左右どちらの手で投げるかを書いています。丸の中の数字は、投げたボールが何拍後にキャッチされるか、曲線はボールの遷移を示しています。この図が1.と2.の条件を満たしていることは容易に分かります。3ボールカスケードでは全てのボールが投げられてから3拍後にキャッチされています。次に、441と呼ばれるパターンのジャグリングダイヤグラムを見てみましょう。

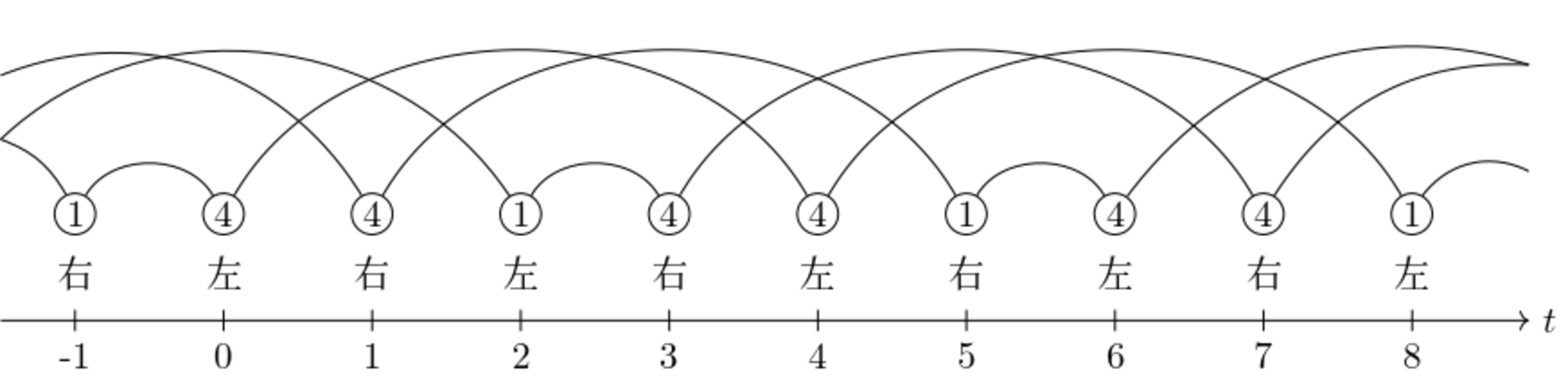441のジャグリングダイヤグラム
このパターンも条件1.、２.を満たしていることが読み取れます。

サイトスワップ

条件1.、2.を満たすジャグリングダイヤグラムの丸の数字を周期的にならない最小の長さ(この長さ $p \in N$ を周期と呼ぶ)だけ抜き出した数列をサイトスワップと呼びます。例えば、3ボールカスケードのサイトスワップは3であり周期は1、441はサイトスワップそのものであり周期は3です。441は144や414と表しても良いです。数の間をカンマで区切ることもありますが、ここではそのまま続けて書くことにします。

サイトスワップには10以上の数字が含まれることもありますが、数字を並べて書いたときに1桁か2桁かを混同してしまうことを避けるため、10以上の数字を $a, b, c, \dots$ と表記します。すなわち、 $a = 10, b = 11, c = 12, \dots, z = 35$ です。人間には35より大きい数字が出でくるようなパターンを投げるのは不可能なので、この記法は35以上の数字に対しては定義されていません。

数学的な定義

次に、サイトスワップを数学的に定義することを目指します。そのために、いくつかの用語を定義します。

ジャグリングパターンと高さ関数

全単射 $f : Z \to Z$ が任意の $t \in Z$ に対し $f (t) \geq t$ かつ、高さ関数 $h_{f} (t) = f (t) - t$ が $h_{f} (t + k p) = h_{f} (t)$ を満たすとき、 $f$ を周期 $p$ のジャグリングパターンと呼ぶ。

$t$ 拍目に投げたボールが、次は $f (t)$ 拍目に投げられる考えてください。 $f (t) \geq t$ は投げたボールが時間を逆行しないことを保証しています。 $f$ が全単射であるということは、条件2.に対応しています。実際、単射でなければ2つ以上のボールを同時にキャッチする拍があることになるので、条件2.を満たしません。また、全射でなければ何も持っていないはずの手からボールを投げることになってしまい不適切です。 $h_{f} (t)$ はジャグリングダイヤグラムにおける丸の中の数字と対応しています。 $h_{f} (t + k p) = h_{f} (t)$ はサイトスワップの周期が $p$ であることから要請されます。

3ボールカスケード

3ボールカスケードでは、
$f (t) = 3 + t, h_{f} (t) = 3$
であることがジャグリングダイヤグラムより読み取れます。

441

441では、
$f (t) = {\begin{cases} 4 + t (t \equiv 0, 1 (\mod 3)) \\ 1 + t (t \equiv 2 (\mod 3)) \end{cases}, h_{f} (t) = {\begin{cases} 4 (t \equiv 0, 1 (\mod 3)) \\ 1 (t \equiv 2 (\mod 3)) \end{cases}$
となります。

では、これらの概念を用いてサイトスワップを定義しましょう。

サイトスワップ

有限非負整数列 ${a_{i}}_{i = 0}^{p - 1}$ に対し、任意の $i \in Z / p Z$ について $h_{f} (i) = a_{i}$ となるようなジャグリングパターン $f : Z \to Z$ が存在する時、数列 ${a_{i}}_{i = 0}^{p - 1}$ をサイトスワップと呼ぶ。また、数列がサイトスワップとなるとき、その数列はJugglableであると言う。

先に挙げた3や441はJugglableな数列です。

Jugglableな数列その1

531はJugglableな数列です。実際、 $f (t) = {\begin{cases} 5 + t (t \equiv 0 (\mod 3)) \\ 3 + t (t \equiv 1 (\mod 3)) \\ 1 + t (t \equiv 2 (\mod 3)) \end{cases}, h_{f} (t) = {\begin{cases} 5 (t \equiv 0 (\mod 3)) \\ 3 (t \equiv 1 (\mod 3)) \\ 1 (t \equiv 2 (\mod 3)) \end{cases}$ とすれば良いことが分かります。

Jugglableな数列その2

a86411はJugglableな数列です。ここで、 $a = 10$ であることに注意してください。

Jugglableではない数列

ap2022はJugglableな数列ではありません。

例4と5はJugglableか判定するのが難しいですが、次で示す判定法を用いれば容易に判断することができます。

Jugglable性の判定

任意の有限非負整数列がサイトスワップになるわけではありません。例えば、21という数列を考えてみましょう。この数列に従ってジャグリングダイヤグラムを考えると次のようになります。

21のジャグリングダイヤグラム？

このダイヤグラムは条件2.を満たしていません。実際、奇数拍で同時に2つのボールをキャッチしていますし、偶数拍では持っていないはずのボールを投げています。よって数列21はJugglableではありません。

定義に沿って数列がJugglableであるかを考えるのは面倒なので、与えられた数列がJugglableであるかを判定する別の方法を考えていきましょう。そのために、2つの補題を示します。

$f$ が周期 $p$ のジャグリングパターン $⟹$ $f (t) + k p = f (t + k p)$ が任意の $t \in Z / p Z, k \in Z$ について成り立つ。

$h_{f} (t + k p) = h_{f} (t)$ より従う。

$f$ を周期 $p$ のジャグリングパターンとする。このとき、
$f^{'} : Z / p Z \to Z / p Z; t ⟼ f (t) (\mod p)$
はwell-definedで全単射。すなわち， $f^{'}$ は $Z / p Z$ の置換である。

補題1より、 $t \equiv s (\mod p)$ ならば $f (t) \equiv f (s) (\mod p)$ である。これはすなわち $t \equiv s (\mod p)$ ならば $f^{'} (s) \equiv f^{'} (t) (\mod p)$ であることを示しているから $f^{'}$ はwell-definedである。次に全単射性を示すが、全射性のみ示せば十分。 $t \in Z / p Z$ とする。 $f$ は全単射であるから、 $f (s) = t$ を満たす $s \in Z$ がある。ここで補題1より、 $s^{'} = s (\mod p)$ とすれば、 $s^{'} \in Z / p Z$ であって $f (s^{'}) \equiv t (\mod p)$ である。よって $f^{'}$ は全射であることが示せた。

補題2はジャグリングパターン $f$ に対しある置換 $π_{f}$ があって、 $f (t) \equiv π_{f} (t) (\mod p)$ が成立することを示しています。以上の補題より、次の定理を得ます。

Jugglable性の判定

有限非負整数列 ${a_{i}}_{i = 0}^{p - 1}$ がJugglableである。 $⟺$ 写像 $ϕ_{{a_{i}}} : Z / p Z \to Z / p Z; i ⟼ a_{i} + i (\mod p)$
が全単射。

( $\Rightarrow$ )数列 ${a_{i}}_{i = 0}^{p - 1}$ がJugglableであるとする。すなわち、あるジャグリングパターン $f$ があって、 $h_{f} (i) = a_{i}$ である。補題2より任意の $i \in Z / p Z$ に対し $f (i) \equiv π_{f} (i) (\mod p)$ となる置換 $π_{f}$ が存在するが、
$a_{i} = h_{f} (i) = f (i) - i \equiv π_{f} (i) - i (\mod p)$
より、 $a_{i} + i \equiv π_{f} (i) (\mod p)$ が得られる。置換は全単射であるから、 $ϕ_{{a_{i}}}$ も全単射である。

( $\Leftarrow$ ) $ϕ_{{a_{i}}}$ が置換であったとする。 ${a_{i}}_{i = 0}^{p - 1}$ がJugglableであることを示すには任意の $i \in Z / p Z$ に対し $h_{f} (i) = a_{i}$ となるようなジャグリングパターン $f$ を見つければ良い。数列 ${a_{i}}_{i = 0}^{p - 1}$ を拡張し、 $j \in Z$ に対し $a_{j} = a_{i} (j \equiv i (\mod p))$ と定義する。ここで、 $f : Z \to Z; j ⟼ a_{j} + j$
という関数を考え、これがジャグリングパターンとなっていることを示す。 $h_{f} (j) = a_{j}$ は $f$ の作り方から満たされていることがすぐ分かるから、任意の $k, j \in Z$ に対し $h_{f} (j + k p) = h_{j} (j)$ 、任意の $i \in Z / p Z$ 対し $f (i) \geq i$ と $f$ が全単射になっていることを確かめれば良い。 $\begin{aligned} h_{f} (j + k p) & = f (j + k p) - (j + k p) \\ = a_{j + k p} \\ = a_{j} + j - j \\ = f (j) - j \\ = h_{f} (j) \end{aligned}$
より $h_{f} (j + k p) = h_{j} (j)$ は成立。また、 $f (i) \geq i$ は $a_{i}$ が非負であることから明らか。
あとは $f$ が全単射であることを示す。

(単射性) $s, t \in Z$ に対し $f (s) = f (t)$ であったとする。このとき、 $f$ の定め方から $ϕ_{{a_{i}}} (s) = ϕ_{{a_{i}}} (t)$ である。 $ϕ_{{a_{i}}}$ は全単射であると仮定しているから、 $s \equiv t (\mod p)$ が成り立つ。すなわち、 $a_{s} = a_{t}$ である。これと $f (s) = f (t)$ より $s = t$ が言えるから、単射性は示された。

(全射性) $ϕ_{{a_{i}}}$ は全単射であるから、ある $s^{'} \in Z / p Z$ に対し、 $ϕ_{{a_{i}}} (s^{'}) \equiv t (\mod p)$ となる $t \in Z$ がある。すなわち、 $a_{s^{'}} + s^{'} \equiv t (\mod p)$ が成り立っている。ここで、 $a_{s^{'}} + s^{'} + k p = t$ とすると、 $a_{s^{'}} = a_{s^{'} + k p}$ であるから
$\begin{aligned} f (s^{'} + k p) & = a_{s^{'} + k p} + s^{'} + k p \\ = a_{s^{'}} + s^{'} + k p \\ = t \end{aligned}$
よって、 $s = s^{'} + k p$ とおけば、任意の $s \in Z$ に対して $f (s) = t$ となる $t \in Z$ がとれるため、 $f$ は全射である。

a86411がJugglableであることを定理1を用いて確かてみましょう。 $a_{0} = a, a_{1} = 8, \dots, a_{5} = 1$ とすると、
$\begin{array}{r} ϕ_{{a_{i}}} (0) = 4, ϕ_{{a_{i}}} (1) = 3, ϕ_{{a_{i}}} (2) = 2 \\ ϕ_{{a_{i}}} (3) = 1, ϕ_{{a_{i}}} (4) = 5, ϕ_{{a_{i}}} (5) = 0 \end{array}$
であるから、 $ϕ_{{a_{i}}}$ は全単射です。よってa86411はJugglableです。

ボールの個数

与えられた数列がJugglableであるかは定理3を用いて判定することができるようになりました。しかし、何個のボールが必要なのかを求めることはできません。実際にジャグリングする際に必要なボールの個数をサイトスワップから求めることを考えてみましょう。

その前に、サイトスワップの重要な性質を導きます。

siteswap

$s = {a_{i}}_{i = 0}^{p - 1}$ を長さ2以上の有限非負整数列とする。 $0 \leq m < n \leq p - 1, n - m < a_{m}$ を満たす $n, m$ に対し、数列 $s_{m, n}$ を
$s_{m, n} = {a_{i}^{'}}_{i = 0}^{p - 1} = {\begin{cases} a_{i} (i \neq m, n) \\ a_{n} + (n - m) (i = m) \\ a_{m} - (n - m) (i = n) \end{cases}$
と定義する。このように、数列 $s$ を $s_{m, n}$ へ変換することをsiteswapと呼ぶ。

同じ名前でややこしいので、この記事では数列を性質を表す方を「サイトスワップ」、数列の変換を表す方を「siteswap」と表記を分けています。

数列 $a_{0} = 4, a_{1} = 6, a_{2} = 1, a_{3} = 3, a_{4} = 1$ に対して $s_{0, 1}$ は $a_{0}^{'} = 6 + (1 - 0) = 7, a_{1}^{'} = 4 - (1 - 0) = 3, a_{2}^{'} = 1, a_{3}^{'} = 3, a_{4}^{'} = 1$ です。

さて、このsiteswapに関して次の2つの定理が成り立ちます。

$s = {a_{i}}_{i = 0}^{p - 1}$ を長さ2以上の有限非負整数列とする。 $s$ がJugglableである $\Leftrightarrow$ $s$ にsiteswapを施した $s_{m, n} = {a_{i}^{'}}_{i = 0}^{p - 1}$ がJugglableである。

$s$ がJugglableであると仮定する。 $s_{m, n}$ の定義より、
$\begin{array}{r} {\begin{cases} a_{n}^{'} + n = a_{m} + m \\ a_{m}^{'} + m = a_{n} + n \\ a_{i}^{'} + i = a_{i} + i (i \neq m, n) \end{cases} \end{array}$
が成り立つ。すなわち、写像
$ϕ_{{a_{i}^{'}}} : Z / p Z \to Z / p Z; i ⟼ a_{i}^{'} + i (\mod p)$
は、写像 $ϕ_{{a_{i}}} : Z / p Z \to Z / p Z; i ⟼ a_{i} + i (\mod p)$ と互換 $(m, n)$ の合成で書ける。 $ϕ_{{a_{i}}}$ と互換 $(m, n)$ は全単射であるから、 $ϕ_{{a_{i}^{'}}}$ も全単射。よって $s_{m, n}$ はJugglableである。逆に関しても同様の議論で示すことができる。

siteswapは数列の平均を保つ。すなわち、
$\frac{1}{p} \sum_{i = o}^{p - 1} a_{i} = \frac{1}{p} \sum_{i = o}^{p - 1} a_{i}^{'}$

$a_{m}^{'} + a_{n}^{'} = a_{n} + (n - m) + a_{m} - (n - m) = a_{n} + a_{m}$ より示せる。

siteswapは数列のJugglable性と平均を保つ変換であることが分かりました。

サイクリックシフト

ここで、また別の操作を定義します。

サイクリックシフト

数列 $s = {a_{i}}_{i = 0}^{p - 1}$ に対し、数列 $s_{\to} = {a_{i - 1 (\mod p)}}_{i = 0}^{p - 1} = a_{p - 1} a_{0} a_{1} \dots a_{p - 2}$ のこと、ないし $s_{\to}$ への変換をサイクリックシフトと呼ぶ。また、 $k$ -シフトを $k$ 回サイクリックシフトを施した数列とし、 $s_{\vec{k}}$ と書く。

サイクリックシフトに対しても同様の定理が成り立ちます。

$s = {a_{i}}_{i = 0}^{p - 1}$ を有限非負整数列とする。 $s$ がJugglableである $\Leftrightarrow$ $s_{\to}$ がJugglableである。

$s$ がJugglableであると仮定する。 $s_{\to}$ の定義より、
$ϕ : Z / p Z \to Z / p Z; i ⟼ a_{i} + i + 1 (\mod p)$
が全単射であることを示せば、 $s_{\to}$ がJugglableであることが示せるが、 $s$ のJugglable性よりこれは明らかに全単射。

サイクリックシフトは数列の平均を保つ。

サイクリックシフトは数列の順番を入れ替えているだけであるから、数列の平均は保たれる。

ジャグリングダイヤグラムを考えれば、サイクリックシフトがJugglable性を保つことは明らかですね。これで441も414も144もJugglableであることが数学的に示せました。

平均の定理

本題に入る前に補題を示します。

${a_{i}}_{i = 0}^{p - 1}$ をJugglableな数列とする。このとき、
$b = \frac{1}{p} \sum_{i = 0}^{p - 1} a_{i}$
は非負整数である。

${a_{i}}_{i = 0}^{p - 1}$ はJugglableであるから、
$\sum_{i = 0}^{p - 1} (a_{i} + i) \equiv \sum_{i = 0}^{p - 1} i (\mod p)$
よって、
$\sum_{i = 0}^{p - 1} (a_{i} + i) \equiv 0 (\mod p)$
${a_{i}}_{i = 0}^{p - 1}$ は非負数列であるから、 $\frac{1}{p} \sum_{i = 0}^{p - 1} a_{i}$ は非負整数である。

さて、ようやく準備が終わりました。以上の道具を用いて2つの定理を示しましょう。

${a_{i}}_{i = 0}^{p - 1}$ をJugglableな数列とし、 $b = \frac{1}{p} \sum_{i = 0}^{p - 1} a_{i}$ とする。このとき、数列 ${a_{i}}_{i = 0}^{p - 1}$ にsiteswapとサイクリックシフトを作用させると数列 $\overset{p 個}{\overset{⏞}{b b \dots b}}$ に変換することができる。

siteswapとサイクリックシフトは逆元を持つ操作であるから、与えられたJugglableな数列 $s = {a_{i}}_{i = 0}^{p - 1}$ にsiteswapとサイクリックシフトを施して $\overset{p 個}{\overset{⏞}{b b \dots b}}$ へと変換できることを示せば良い。そこで、以下のアルゴリズムを考える。

$s$ が定数列であれば操作を終える。そうでないならば2.へ進む。
$i$ を $a_{i}$ が $s$ の中で最大かつ $a_{i + 1} < a_{i}$ となるように選ぶ。 $s$ にi-シフトを施し、先頭に $a_{i}$ が、その次に $a_{i + 1}$ が来るようにし、3.へ進む。
$s \to s_{1, 2}$ とsiteswapを施し、1.へ戻る。

手順2.で $a_{i} - a_{i + 1} = 1$ の場合は手順3.でsiteswapを施しても最大値と最大値をとる $a_{i}$ の個数は変わらない。しかし、 $s$ はJugglableであるから、定理3より $a_{i} - a_{i + 1} = 1$ とはなり得ない。よって、手順3.によって数列 $s$ の最大値は必ず1だけ減るか、または最大値をとる $a_{i}$ の個数が1だけ減る。よってこのアルゴリズムは有限回で終了し、それは $s$ が定数列へと変換された時である。さらに定理5と7より数列の平均は保たれるから、このアルゴリズムで数列は $\overset{p 個}{\overset{⏞}{b b \dots b}}$ へ変換されることが分かる。

平均の定理

${a_{i}}_{i = 0}^{p - 1}$ をJugglableな数列とする。このとき、
$b = \frac{1}{p} \sum_{i = 0}^{p - 1} a_{i}$
とすると、 $b$ は ${a_{i}}_{i = 0}^{p - 1}$ をジャグリングをするのに必要なボールの個数と一致する。

$\overset{p 個}{\overset{⏞}{b b \dots b}}$ をジャグリングするにはb個のボールが必要なのは明らか(b拍後に手に戻ってくる高さでボールを投げ続けるため、b個のボールが必要)。この事実と定理4、6、9より、数列の平均 $b$ は必要なボールの数と一致することが分かる。

長い道のりでした。これで与えられた数列がJugglableであるか、実際にジャグリングをするには何個のボールが必要なのかを判別できます。ちなみに、補題8は定理3と共にJugglable性の判定によく用いられます。

Jugglableな数列46131が数列33333に変換できることを確かめてみましょう。
$46131 \overset{シフト}{⟶} 61314 \overset{s w a p}{⟶} 25314 \overset{シフト}{⟶} 53142 \overset{s w a p}{⟶} 44142 \overset{シフト}{⟶} 41424$
$\overset{s w a p}{⟶} 23424 \overset{シフト}{⟶} 42423 \overset{s w a p}{⟶} 33423 \overset{シフト}{⟶} 42333 \overset{s w a p}{⟶} 33333$
$(4 + 6 + 1 + 3 + 1) \nabla \cdot 5 = 3$ ですから、定理9の主張を再現できていることが分かります。