下降冪版二項定理と上昇冪版二項定理
以前このサイトで子葉さんのヴァンデルモンドの恒等式の記事を見たときに思った事を書こうと思います。
ポッホハマー記号 $(x){}_k=x(x-1)(x-2)(x-3)…(x-k+1)= \frac{x!}{x-k!}$
($x+y$)${}_n$=$\sum_{k=0}^{n}$$
\binom{n}{k} (x) {}_k(y){}_n{}_-{}_k
$$
$
が成り立つなら逆も成り立つと思い
ポッホハマー記号 $(x){}^k=x(x+1)(x+2)(x+3)…(x+k-1)=
\frac{x+k-1!
}{x-1!}
$$
$
（$x+y$)${}^n$=$ \sum_{k=0}^{n}$$
\binom{n}{k} (x){}^k(y){}^n{}^-{}^k
$
も成り立つことを発見しました。
$(x+y){}^n{}^+{}^1=(x+y+n)(x+y){}^n$
$= \sum_{k=0}^{n}((x+k)+(y+(n-k)))\binom{n}{k}(x){}^k(y){}^n{}^-{}^k$
$= \sum_{k=0}^{n}
\binom{n}{k}
((x){}^k{}^+{}^1(y){}^n{}^-{}^k+(x){}^k(y){}^n{}^+{}^1{}^-{}^k)
$
$= \sum_{k=1}^{n+1}
\binom{n}{k-1}
(x){}^k(y){}^n{}^+{}^1{}^-{}^k+ \sum_{k=0}^{n}
\binom{n}{k}
(x){}^k(y){}^n{}^+{}^1{}^-{}^k$
$= \sum_{k=0}^{n+1}($$
\binom{n}{k-1}
$$+$$
\binom{n}{k}
$$)(x){}^k(y){}^n{}^+{}^1{}^-{}^k$
$= \sum_{k=0}^{n+1}$$
\binom{n+1}{k}
$$(x){}^k(y){}^n{}^+{}^1{}^-{}^k$
これをヴァンデルモンドの恒等式みたいに二項係数にすると、
$(x){}^n=(x+n-1){}_n$
$(x+y){}^n=(x+y+n-1){}_n$
なので、
$ $$
\binom{x+y+n-1}{n}
$$=
\sum_{i=0}^{n} \frac{x+i-1!}{x-1!i!} \frac{y+(n-i)-1!}{y-1!(n-i)!}$ $= \sum_{i=0}^{n}
\binom{x+i-1}{i}
\binom{y+(n-i)-1}{(n-i)}
$$
$$
$
$ {}_ =(x+y)\mathrm{ H }_n= \sum_{i=0}^{n} {}_x \mathrm{ H }_i× {}_y \mathrm{ H }_(n-i) $
$ (x+y)^n=\frac{x+y+n-1!}{x+y-1!}$
$=n!\frac{x+y+n-1!}{n!(x+y-1)!}$
$=n!\begin{eqnarray}
\left(
\begin{array}{cc}
x+y+n-1 \\
n
\end{array}
\right)
\end{eqnarray}$
$=\sum_{i=0}^{n}\begin{eqnarray}
\left(
\begin{array}{cc}
n \\
i
\end{array}
\right)
\end{eqnarray}(x)^{i}(y)^{n-i}$
$=\sum_{i=0}^{n}\frac{n!}{i!(n-i)!}\frac{x+i-1!}{(x-1)!}\frac{y+(n-i)-1!}{(y-1)!}$
$=n!\sum_{i=0}^{n}\frac{x+i-1!}{i!(x-1)!}\frac{y+(n-i)-1!}{(n-i)!(y-1)!}
$
その場合$y$が1のときホッケースティック恒等式と等価になることが分かった。
$
\binom{x+n}{n} = \sum_{i=0}^{n}
\binom{x+i-1}{x-1} \binom{(n-i)}{(n-i)}
$ $ =\sum_{i=0}^{n}\binom{x+i-1}{i}$
これは$
\binom{n+n}{n}=\binom{2n}{n}
=\sum_{i=0}^{n}\binom{n+i-1}{i}$
となり、ホッケースティック恒等式は中心二項係数になる。
そして今、示した上の形式のホッケースティック恒等式を、$n$を$0$の場合から下にかけて増やしながら表わすと、重複組合せによるパスカルの三角形が出来上がる。そしてその段ごとの和は中心二項係数となることが分かりました。
$\begin{eqnarray}
\left(
\begin{array}{cc}
x+n \\
n
\end{array}
\right)
\end{eqnarray}$ $=\sum_{i=0}^{n}\begin{eqnarray}
\left(
\begin{array}{cc}
x+i-1 \\
i
\end{array}
\right)
\end{eqnarray}$
$\begin{eqnarray}
\left(
\begin{array}{cc}
x+n \\
x
\end{array}
\right)
\end{eqnarray}$=$\sum_{i=0}^{n}\begin{eqnarray}
\left(
\begin{array}{cc}
x+i-1 \\
x-1
\end{array}
\right)
\end{eqnarray}$
$\begin{eqnarray}
\left(
\begin{array}{cc}
x+n \\
x
\end{array}
\right)
\end{eqnarray}$=$\sum_{i-1=x-1}^{x+n-1}\begin{eqnarray}
\left(
\begin{array}{cc}
i-1 \\
x-1
\end{array}
\right)
\end{eqnarray}$
$\begin{eqnarray}
\left(
\begin{array}{cc}
x+n+1 \\
x+1
\end{array}
\right)
\end{eqnarray}$=$\sum_{i=x}^{x+n}\begin{eqnarray}
\left(
\begin{array}{cc}
i \\
x
\end{array}
\right)
\end{eqnarray}$
$x+n=y$として
ホッケースティック恒等式である
$\begin{eqnarray}
\left(
\begin{array}{cc}
y+1 \\
x+1
\end{array}
\right)
\end{eqnarray}$=$\sum_{i=x}^{y}\begin{eqnarray}
\left(
\begin{array}{cc}
i \\
x
\end{array}
\right)
\end{eqnarray}$
になります。
一般$ \Longrightarrow $特殊
とすれば、
$$
\begin{eqnarray}二項定理
\left\{
\begin{array}{l}下降冪版二項定理 \Longrightarrowヴァンデルモンドの恒等式
\cdots \\上昇冪版二項定理 \Longrightarrow今回発見した恒等式 \Longrightarrowホッケースティック恒等式
\cdots
\end{array}
\right.
\end{eqnarray}
$$
となるみたいです。
ホッケースティック恒等式はパスカルの三角形で表したら、ホッケースティックみたいな形だからそう言われるようになったそうです。ならば今回発見した恒等式はパスカルの三角形で表すと二つに分かれているので、チョップスティック(箸)恒等式とでも言いましょうか(笑)
図にして例を作ります。
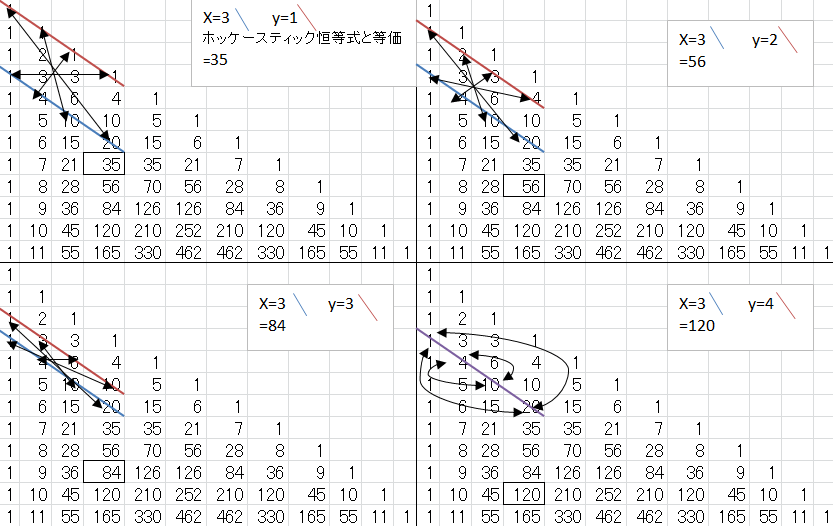パスカルの三角形上の恒等式
赤線、青線上の↔同士を掛け算したものを、足し算したものが今回の恒等式です。
$y$の赤線が下がって行くほど、解の数も下がって行くのが分かります。
また、パスカルの三角形の法則を使うと
$
\begin{eqnarray}
\left(
\begin{array}{cc}
n \\
r
\end{array}
\right)
\end{eqnarray}
=$$\begin{eqnarray}
\left(
\begin{array}{cc}
n-1 \\
r-1
\end{array}
\right)
\end{eqnarray}
+$$
\begin{eqnarray}
\left(
\begin{array}{cc}
n-1 \\
r
\end{array}
\right)
\end{eqnarray}
$なのでホッケースティック恒等式の解が$\begin{eqnarray}
\left(
\begin{array}{cc}
n-1 \\
r
\end{array}
\right)
\end{eqnarray}$だとすれば、それに$\begin{eqnarray}
\left(
\begin{array}{cc}
n-1 \\
r-1
\end{array}
\right)
\end{eqnarray}$を足して,答えである$\begin{eqnarray}
\left(
\begin{array}{cc}
n \\
r
\end{array}
\right)
\end{eqnarray}$にたどり着く。
$y=1$ならホッケースティック恒等式なので何も足さない。
$y=2$ならパスカルの三角形の法則を使う$\begin{eqnarray}
\left(
\begin{array}{cc}
n-1 \\
r-1
\end{array}
\right)
\end{eqnarray}$を足す。
$y=3$以降はホッケースティック恒等式 を使う。因みに$y=3$の場合は$\begin{eqnarray}
\left(
\begin{array}{cc}
n-1 \\
r-1
\end{array}
\right)
\end{eqnarray}$と$\begin{eqnarray}
\left(
\begin{array}{cc}
n-2 \\
r-1
\end{array}
\right)
\end{eqnarray}$を足していく様にすると、掛け算をしなくても、今回の記事にした恒等式の解が出る。
この記事を高評価した人
この記事に送られたバッジ
投稿者
