差動入力増幅器の出力電圧　理論計算(仮稿)

"MathLog"には似合わず電子回路の計算になりますがお付き合いください．

図の差動入力増幅回路(differential input amplifier)における出力電圧$V_o$を計算していきます．

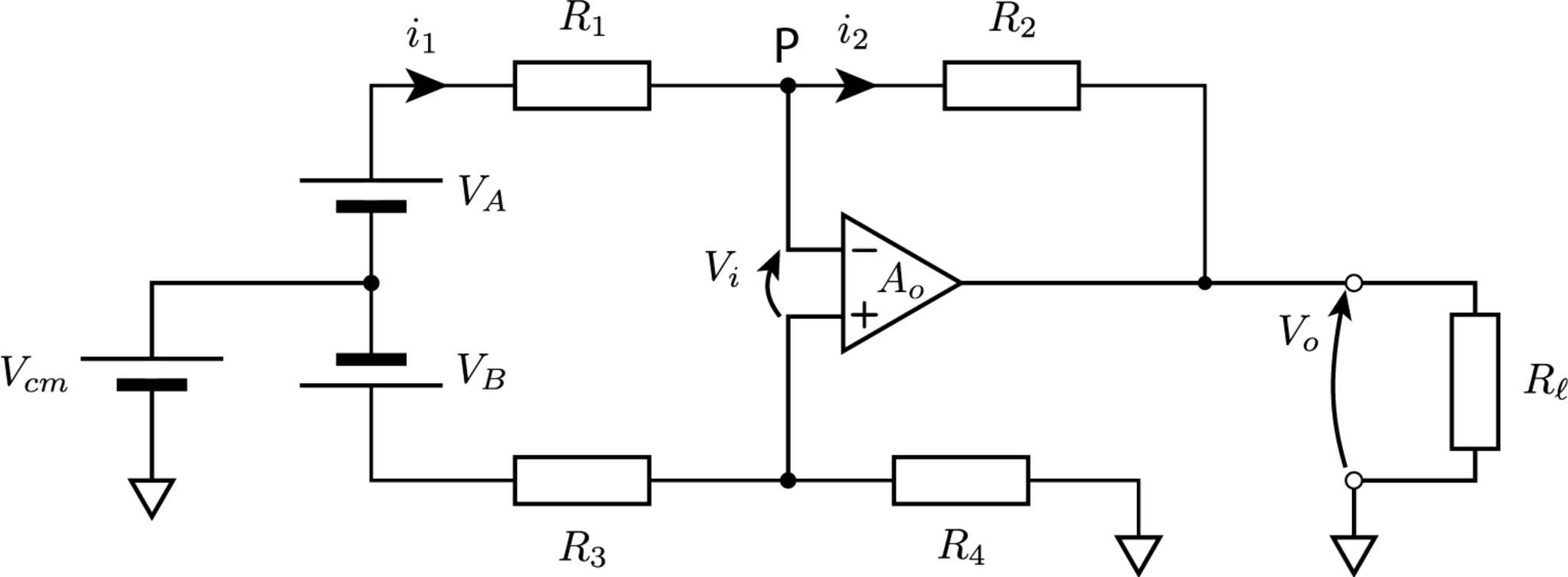差動入力増幅器(differential input amplifier)

〈仮定〉オペアンプは理想オペアンプであるとし，入力電流$i_{in}=0$，オペアンプの端子間電圧$v_i=0$とします．

抵抗$R_4$の両端電圧$V_4$は，common-mode(共通モード)電圧を$V_{cm}$として，以下で示されるでしょう．
$$V_4=(V_{cm}+V_B)\times\frac{R_4}{R_3+R_4}$$
また，点PにおけるKCL(Kirchhoff's Current Law)より，$i_1=i_2$であるから，
$$i_1=\frac{V_{cm}+V_A-V_4}{R_1}=i_2=\frac{V_4-V_o}{R_2}.$$
両辺に$R_1R_2$をかけて，
$$\begin{align}R_2(V_{cm}+V_A-V_4)&=R_1(V_4-V_o)\\ R_2V_{cm}+R_2V_A-R_2V_4&=R_1V_4-R_1V_o\\ R_1V_o&=R_1V_4+R_2V_4-R_2V_A-R_2V_{cm}\\ &=(R_1+R_2)V_4-R_2(V_A+V_{cm}) \end{align}$$
となりますが，ここに$V_4=(V_{cm}+V_B)\times\frac{R_4}{R_3+R_4}$を代入して展開すると，
$$\begin{align} R_1V_o&=(R_1+R_2)\times(V_{cm}+V_B)\times\frac{R_4}{R_3+R_4}-R_2(V_A+V_{cm})\\ &=\{(R_1+R_2)V_{cm}+(R_1+R_2)V_B\}\times\frac{R_4}{R_3+R_4}-R_2V_A-R_2V_{cm}\\ &=\frac{(R_1+R_2)R_4}{R_3+R_4}V_{cm}+\frac{(R_1+R_2)R_4}{R_3+R_4}V_B-R_2V_A-R_2V_{cm} \end{align}$$
となります．さらに辺々$R_1$で割って$V_{cm}$と$V_A$と$V_B$でまとめると，
$$\begin{align} V_o&=\frac{1}{R_1}\left\{\frac{(R_1+R_2)R_4}{R_3+R_4}V_{cm}-R_2V_{cm}+\frac{(R_1+R_2)R_4}{R_3+R_4}V_B-R_2V_A\right\}\\ &=\frac{1}{R_1}\left\{\frac{(R_1+R_2)R_4}{R_3+R_4}V_{cm}-\frac{R_2(R_3+R_4)}{R_3+R_4}V_{cm}+\frac{R_1R_4+R_2R_4}{R_3+R_4}V_B-R_2V_A\right\}\\ &=\frac{1}{R_1}\left\{\frac{R_1R_4+\cancel{R_2R_4}-R_2R_3-\cancel{R_2R_4}}{R_3+R_4}V_{cm}+\frac{R_1R_4+R_2R_4}{R_3+R_4}V_B-R_2V_A\right\}\\ &=\frac{1}{\cancel{R_1}}\left\{\frac{\cancel{R_1}R_4}{R_3+R_4}V_{cm}-\frac{R_2R_3}{R_3+R_4}V_{cm}+\frac{\cancel{R_1}R_4}{R_3+R_4}V_B+\frac{R_2R_4}{R_3+R_4}V_B-R_2V_A\right\}\\ &=\frac{R_4}{R_3+R_4}V_{cm}-\frac{R_2}{R_1}\frac{R_3}{R_3+R_4}V_{cm}+\frac{R_4}{R_3+R_4}V_B+\frac{R_2}{R_1}\frac{R_4}{R_3+R_4}V_B-\frac{R_2}{R_1}V_A\\ &=\left(\frac{R_4}{R_3+R_4}-\frac{R_2}{R_1}\frac{R_3}{R_3+R_4}\right)V_{cm}+\left(\frac{R_4}{R_3+R_4}+\frac{R_2}{R_1}\frac{R_4}{R_3+R_4}\right)V_B-\frac{R_2}{R_1}V_A \end{align}$$

以上が差動入力増幅器の出力電圧となります．

さらにここから，平衡条件：$\frac{R_2}{R_1}=\frac{R_4}{R_3}$を満たすとき，非常に有用な挙動をします．この平衡条件の値を$\alpha=\frac{R_2}{R_1}=\frac{R_4}{R_3}$とおくと，
$$\frac{R_4}{R_3+R_4}=\frac{R_4/R_3}{1+R_4/R_3}=\frac{\alpha}{1+\alpha}$$
となるので，
$$\begin{align} V_o&=\left(\frac{R_4}{R_3+R_4}-\frac{R_2}{R_1}\frac{R_\textcolor{red}{4}}{R_3+R_4}\right)V_{cm}+\left(\frac{R_4}{R_3+R_4}+\frac{R_2}{R_1}\frac{R_4}{R_3+R_4}\right)V_B-\frac{R_2}{R_1}V_A\\ &=\left(\frac{\alpha}{1+\alpha}-\alpha+\alpha\times\frac{\alpha}{1+\alpha}\right)V_{cm}+\left(\frac{\alpha}{1+\alpha}+\alpha\times\frac{\alpha}{1+\alpha}\right)V_B-\alpha V_A\\ &=\frac{\alpha-\alpha(1+\alpha)+\alpha^2}{1+\alpha}V_{cm}+\frac{\alpha+\alpha^2}{1+\alpha}V_B-\alpha V_A\\ &=\cancel{\frac{\alpha-\alpha-\alpha^2+\alpha^2}{1+\alpha}V_{cm}}+\frac{\alpha\cancel{(1+\alpha)}}{\cancel{1+\alpha}}V_B-\alpha V_A\\ &=\alpha V_B-\alpha V_A\\ &=\alpha(V_B-V_A)=\frac{R_2}{R_1}(V_B-V_A) \end{align}$$
この式から得られることは，以下のようになるでしょう．

以上です．お付き合いいただきありがとうございました．