2019年福島県高校入試の数学を解説

前置き

Q: なんで福島県なの？

僕の地元だからです

Q: なんで2019年なの？

ラス問の正答率が0%で中々インパクトが大きいから

ではやっていきましょう
問題はこちらです

大問1

大問1は基本的に四則演算の問題です

(1)

① $45$

② 通分して
$ -\frac{15}{20} + \frac{8}{20} = -\frac{7}{20} $

③ $-8y^2$

④ 有理化したりして
$ 3\sqrt{6} + 2\sqrt{6} = 5\sqrt{6} $

(2)

反比例の一般式はこいつ
$ y = \frac{a}{x} (x≠0) $

表から、この関数が$(x, y) = (2, 24)$をとることがわかるので、以下の等式が成り立ちます
$ 24 = \frac{a}{2} $

これを解いて、
$ a = 48 $

したがって、この表が示す反比例の式は以下であることが分かります
$ y = \frac{48}{x} $

試しにx=4を代入すると、y=12となり、表と一致します
また、x=6を代入すると、y=8が得られます
よって答えは 8

大問2

ここは色んな分野の小問集合となってます

(1)

$ x^2-8x-20 \\ = (x-10)(x+2) $

(2)

折り紙の総数は
$ 4a+3b $
これが100枚では足りない、すなわち100枚より大きくなってしまうので、
$ 100 < 4a+3b $

(3)

なんか文章が長いですね()
当たり前ですが、給水管の本数を多くすればするほど水の増加量は大きくなります
つまり、給水管の本数を多くするほど直線の傾きは大きくなる
ことがわかります
さて、A, B, C, Dのそれぞれの区間での直線の傾きをそれぞれa, b, c, dとおくと、以下の関係が成り立ちます
$ b = d < a < c $

使う給水管の本数は3本なので、一番増加量が大きいCが3本、その次に大きいAが2本、一番少ないB, Dが1本であることがわかります
よって、答えは エ

(4)

円錐Bの高さを$h$、底面の半径を$r$とすると、円柱Aの底面の半径は$2r$と表せます
円柱Aの体積を$ V_A $、円錐Bの体積を$ V_B $とすると
$ V_A = 4πhr^2 \\ V_B = \frac{1}{3}πhr^2 $

円錐の体積を求めるときは、$ ×\frac{1}{3} $するのを忘れないように __
求めるのは、$ V_A $が$ V_B $の何倍かなので
$ \frac{V_A}{V_B} = 12 $
よって、__12倍

(5)

1. 点Bに針を刺し、線分ABを半径とする円を描く
2. 点Cに針を刺し、線分ACを半径とする円を描く
3. 1, 2で描いた円の交点のうち、点Aでない方を点Pとする
4. PとB、PとCを結ぶ

大問3

ここは確率、統計、規則性のうち2分野が出題されます(大体は今回のように確率、統計が出ます)

(1)

大きいさいころの出た目を$a$、小さいさいころの出た目を$b$とします
ただし、$ 1 ≦ a ≦ 6 $,　$ 1 ≦ b ≦ 6 $

①

$ a+b = 7$
これを満たす$a, b$の組は
$ (a, b) = (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1) $
よって 6通り

➁

$ 1 ≦ a ≦ 6 $,　$ 1 ≦ b ≦ 6 $ より $ 2 ≦ a + b ≦ 12 $
この範囲に存在する素数は $2, 3, 5, 7, 11$の5つです
和が$2$になる$a, b$の組は $(a, b) = (1, 1)$
和が$3$になる$a, b$の組は $(a, b) = (1, 2), (2, 1)$
和が$5$になる$a, b$の組は $(a, b) = (1, 4), (2, 3), (3, 2), (4, 1)$
和が$7$になる$a, b$の組は $(a, b) = (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)$
和が$11$になる$a, b$の組は $(a, b) = (5, 6), (6, 1)$

以上より、和が素数になる組は$15通り$です
さいころの目の出方の総数は、$6 × 6 = 36通り$
よって、和が素数になる確率は
$\frac{15}{36} = \frac{5}{12}$

(2)

①

度数が最も大きい階級は、$210～220$のところ
よって、階級値を計算すると
$\frac{220+210}{2} = 215(cm)$

➁

1組男子の、220cm以上の生徒の割合は
$\frac{3+2+1}{16} = \frac{3}{8}$

3学年男子の、220cm以上の生徒の割合は
$\frac{12+9+7+5}{75} = \frac{11}{25}$

この2つを通分すると
$\frac{3}{8} = \frac{75}{200}$
$\frac{11}{25} = \frac{88}{200}$

よって
$\frac{3}{8} < \frac{11}{25}$

以上から、1組男子は3学年男子と比較して記録の多い生徒が多いとは言えない
したがって、回答は イ

大問4

大問4は連立方程式、もしくは2次方程式の記述式の設問になります
今回は連立方程式です

回答

単品ノートの売れた冊数を$x$冊、単品消しゴムの売れた個数を$y$個とする

セットAとして売れたノートの冊数は $3x-1$冊と表せる
セットAは、ノート1冊、消しゴム1個の組で売っているので、セットAとして売れた消しゴムの個数も$3x-1$個と表せる

また、セットBとして売れた消しゴムの個数は $2y$個と表せる
セットBは、ノート3冊、消しゴム1個の組で売っているので、セットAとして売れたノートの個数は$6y$冊と表せる

以上から、ノートの売れた冊数について、下式が成り立つ
$x + (3x-1) + 6y = 41$
$4x + 6y = 42$ ・・・①

また、売り上げについて、下式が成り立つ
$120x + 160(3x-1) + 60y + 370 × 2y = 5640$
$600x + 800y = 5800$
$6x + 8y = 58$ ・・・➁

①, ➁を連立方程式として解くと
$x=3, y=5$
これらは適している
よって
単品ノートの売れた冊数は$3$冊
単品消しゴムの売れた個数は$5$個

ポイント

赤字の部分に気付けるかどうかですね
計算結果に極端な数字($x=1, x=40$等)が出てきたら、立てた式に間違いがないか確認するようにしたらいいかも(ただし、極端な数字が答えになる可能性は否定できません)

大問5

さて、福島の数学は主に図形分野が難しいです
ここから先は図形分野、つまりここから難しくなります
大問5は基本証明一題ですが、まれに二題になるときがあります(この年は二題の年でした)

(1)

条件通りに書いてくと、以下のような図になります(Googleフォトの雑な線ですみません)

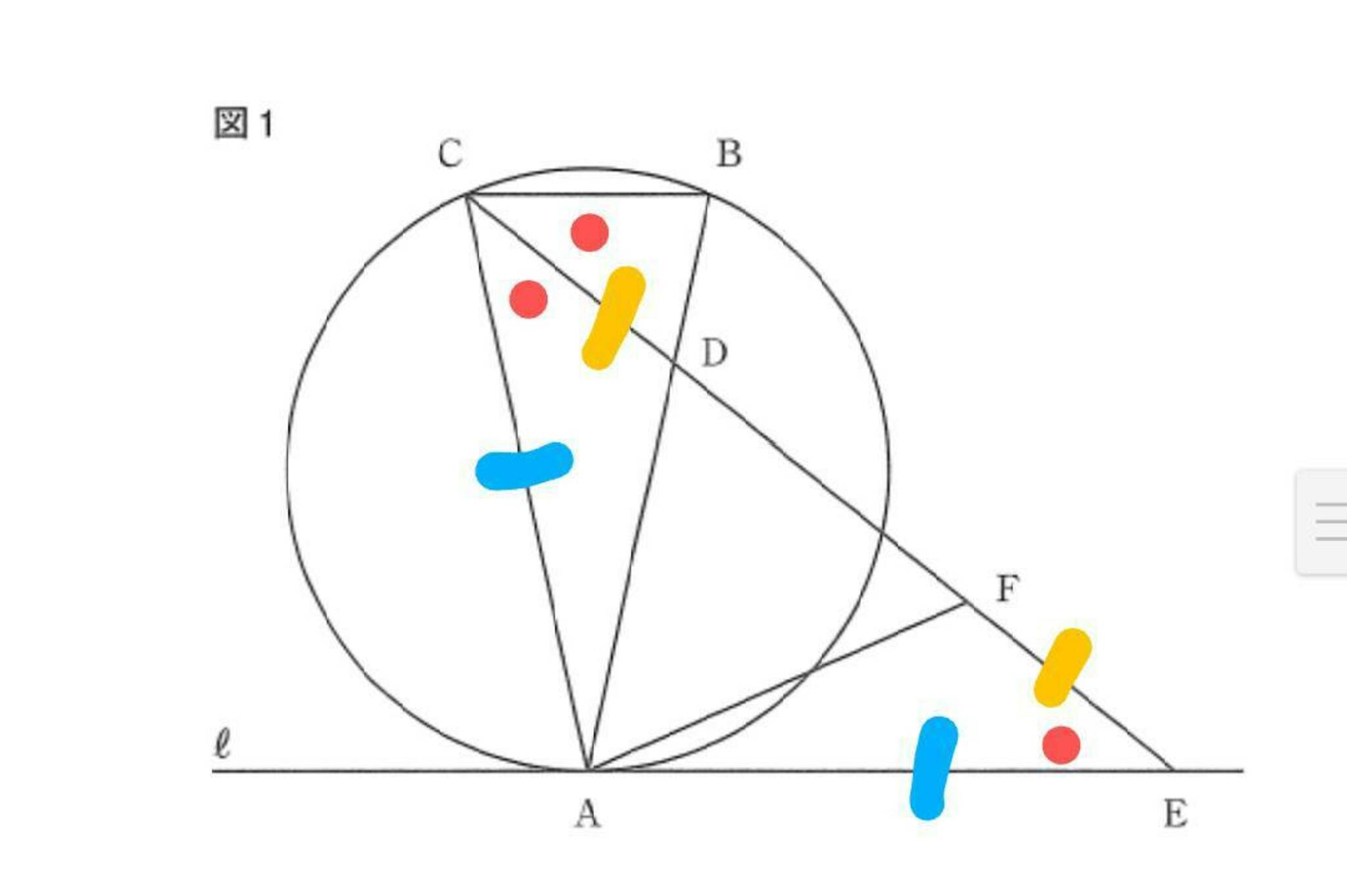大問5 図

△ACEの二等辺三角形が透けましたね

∠AFD=∠ADFを示せればいいので、△ADFが二等辺三角形であることが示せれば良さそうです

これらをもとに証明していきましょう

証明

仮定から、
CD=EF ...①
∠ACD=∠BCD ...➁
BC//ℓより、平行線の錯角は等しいから、∠BCD=∠AEF ...➂
➁, ③より、∠ACD=∠AEF ...④
2つの角が等しいから、△ACEは二等辺三角形である
したがって、AC=AE ...⑤
①, ④, ⑤より、△ACD≡△AEF
よって、AD=AF
二辺が等しいので、△ADFは二等辺三角形である
よって、∠AFD=∠ADF

(2)

具体的な角度が与えられていないとき、大抵直角二等辺三角形か正三角形が混じっているものですが、これは見たところなさそうです

わかってる条件を書き出すと以下のようになります

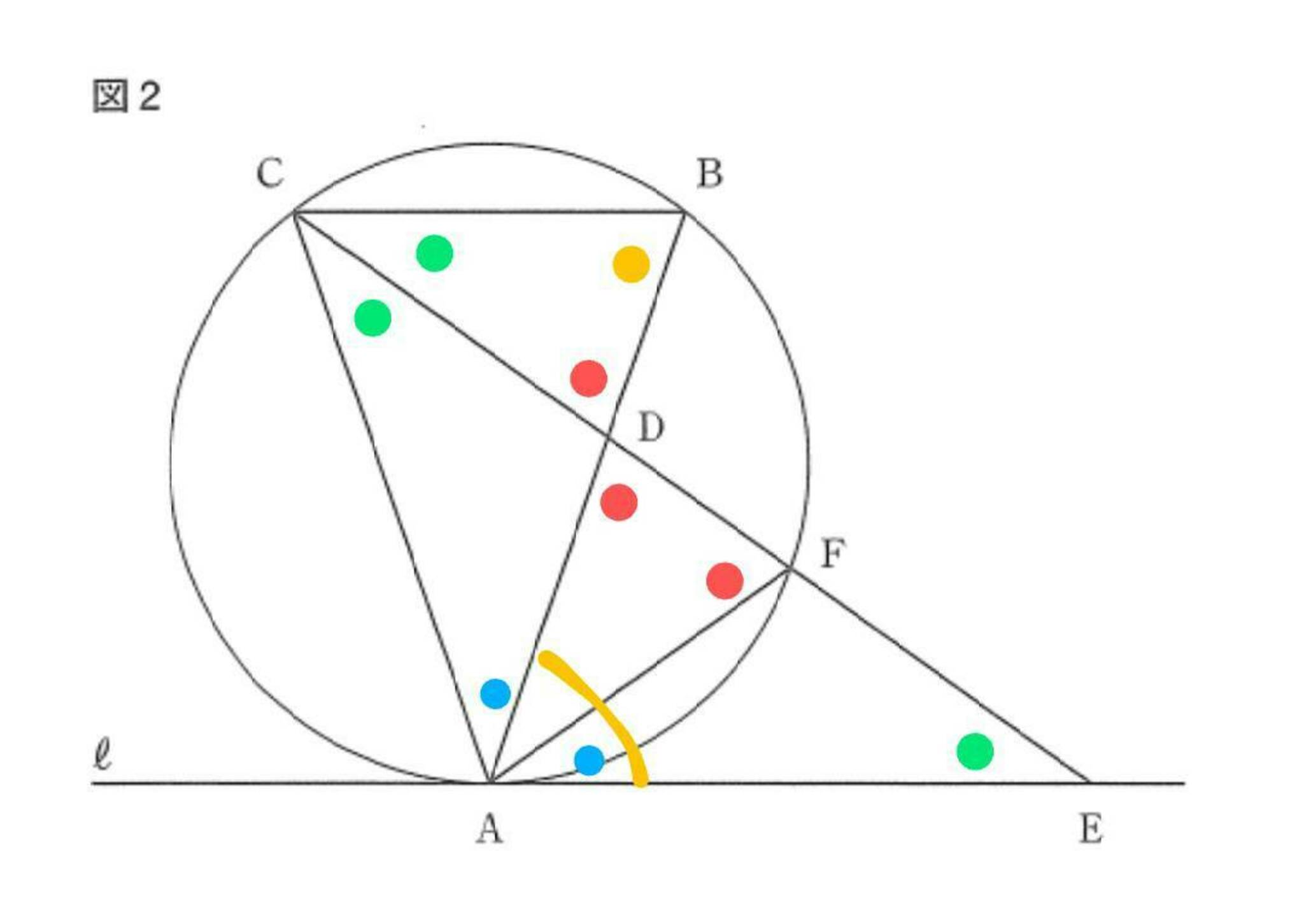大問5(2)1

これだけでは求まりそうにないですね...

さて、円と角度に関する重要な定理を覚えているでしょうか

そうです、__円周角の定理__です
弧BF及び弧ACに円周角の定理を用いると

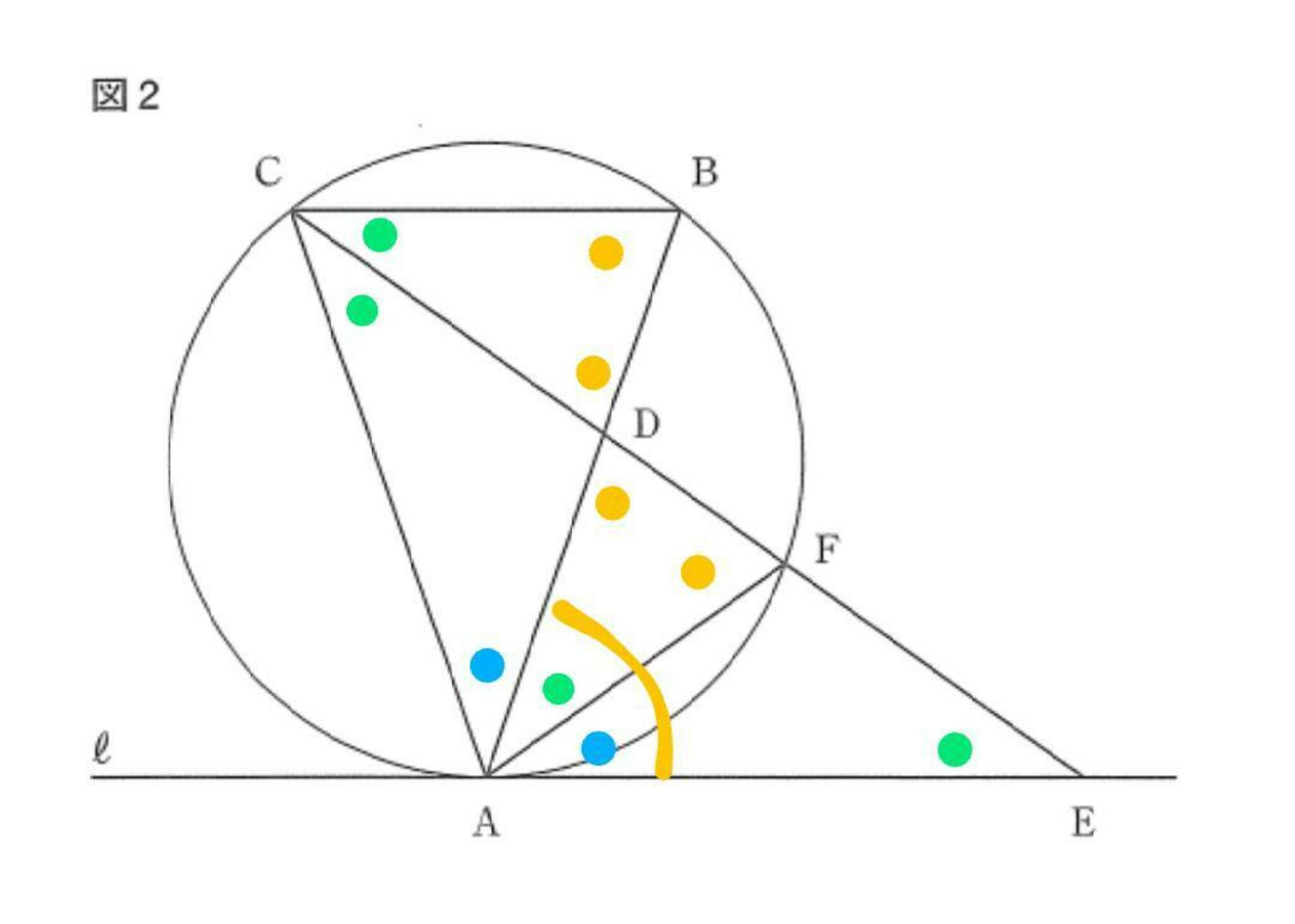大問5(2)2

行けそうな気がしますね

いいところまで来ましたが、あと一歩足りません
なので一本線を引きましょう

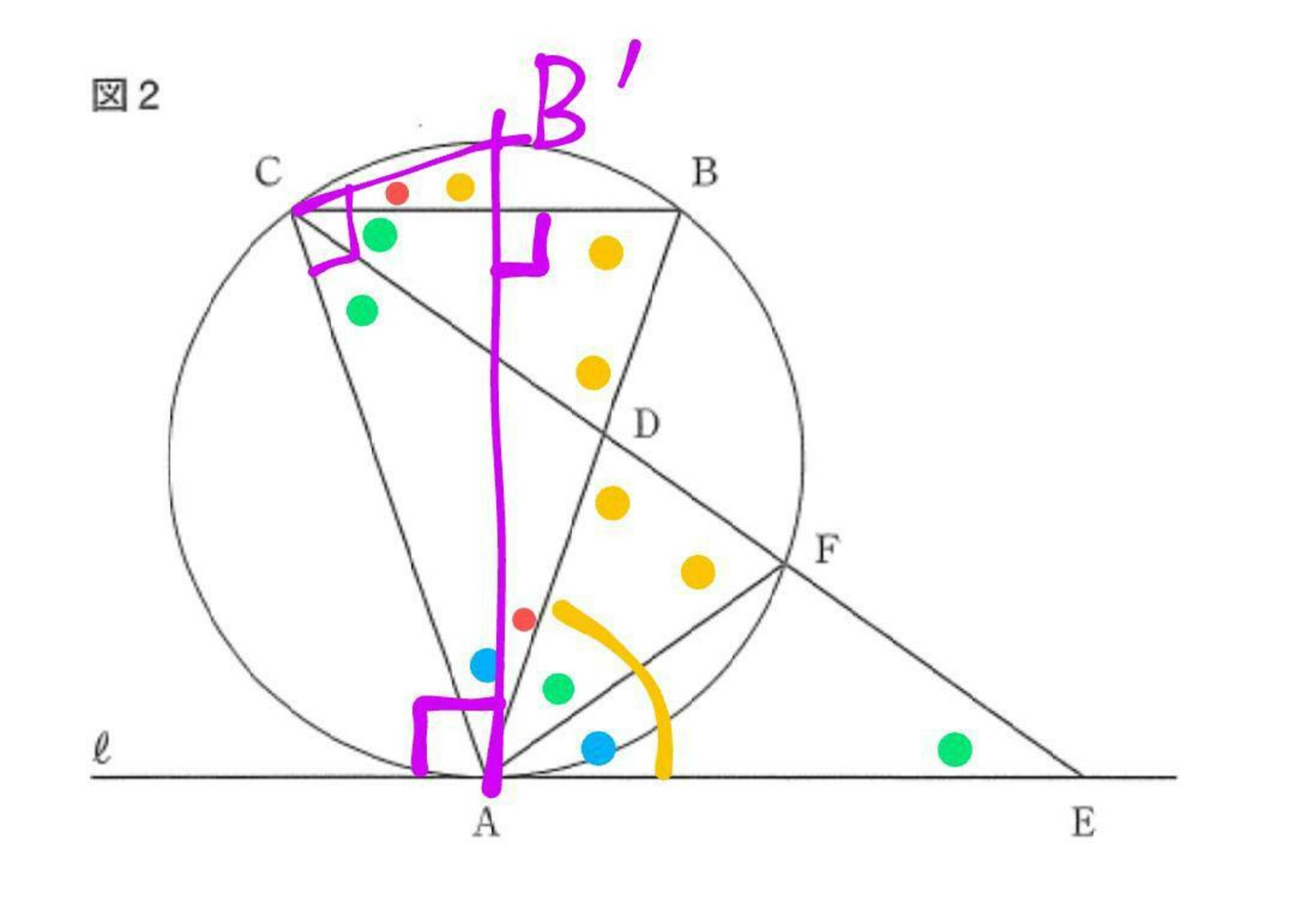大問5(2)3
円周角の定理を利用して、∠ACB'=90°となるように点Bを点B'に移動しました

円周角が直角なので、AB'はこの円の直径になります
円の接点を通る直径は、その接線に対して垂直に交わります
よって、$∠EAB'=90°$

さて、この図を見て気づきますか？

そう、__90°=赤+緑+緑=赤+緑+青__なんです！

したがって、緑=青が成り立ちます

また、∠BAEから、緑+青=黄も成り立ちます

緑の部分の角度を$a$、$∠ABC=x$とすると
$a = 180-2x$

$2a = x$
$2(180°-2x) = x \\ 5x = 360° \\ x = 72°$

よって、答えは 72°

(高校生以上の方はわかると思いますが、この解き方の原理は正弦定理です
正直、本番でこれが出たら捨てていいと思います)

大問6

ここは関数のグラフに関する問題が出題されます

(1)

$A(-3, 9)$
$B(-1, 1)$
です
よって、傾きは
$\frac{1-9}{-1-(-3)}$
$= -4$

(2)

①

$C(2, 4)$
直線mの式を$y=-4x+b$とおくと、点Cを通るから
$4 = -8 + b \\ b = 12$

よって
$D(0, 12)$

直線BCを$y=cx+d$とし、y軸との交点をEとすると、
2点B, Cを通るから
$1 = -c + d$
$4 = 2c + d$
これを連立方程式として解いて
$c=1, d=2$
よって
$E(0, 2)$

以上から
$△BCD = △BDE + △CDE$
$= 10 × 1 × \frac{1}{2} + 10 × 2 × \frac{1}{2}$
$= 15$

➁

$P(t, t^2)$
$Q(t, -4t+12)$

直線ADの傾きを求めると
$\frac{12-9}{3} \\ = 1$

これは直線BCの傾きと一致する
よって、直線AD // 直線BC

また、ℓ // m なので、四角形ABCDは平行四辺形である

よって
$□ABCD = 2△BCD \\ = 30$

また、
$□BPCQ = △BPQ + △CPQ$
$= \frac{(t+1)(-t^2-4t+12)}{2} + \frac{(2-t)(-t^2-4t+12)}{2}$
$= \frac{3}{2}(-t^2-4t+12)$

以上より
$\frac{3}{2}(-t^2-4t+12) = 30 × \frac{1}{5}$
$-t^2-4t+8 = 0$
$t^2+4t-8 = 0$
$(t+2)^2-12 = 0$
$t = -2±2\sqrt{3}$

$0 < t < 2$より
$t = -2+2\sqrt{3}$

大問7

大問7は空間図形の問題となります
特に3つ目の設問は例年正答率が低く、この年に至っては__正答率0%をたたき出しました__(0.0%ではないため、一応正答者自体はいる)

(1)

三平方の定理により
$OM^2 + BM^2 = OB^2$
$OM^2 = 144 - 36$
$OM = 6\sqrt{3} (cm)$

(2)

①

長さの和が最小になるといったら、__直線になればいい__ですよね

以下、展開図で考えます

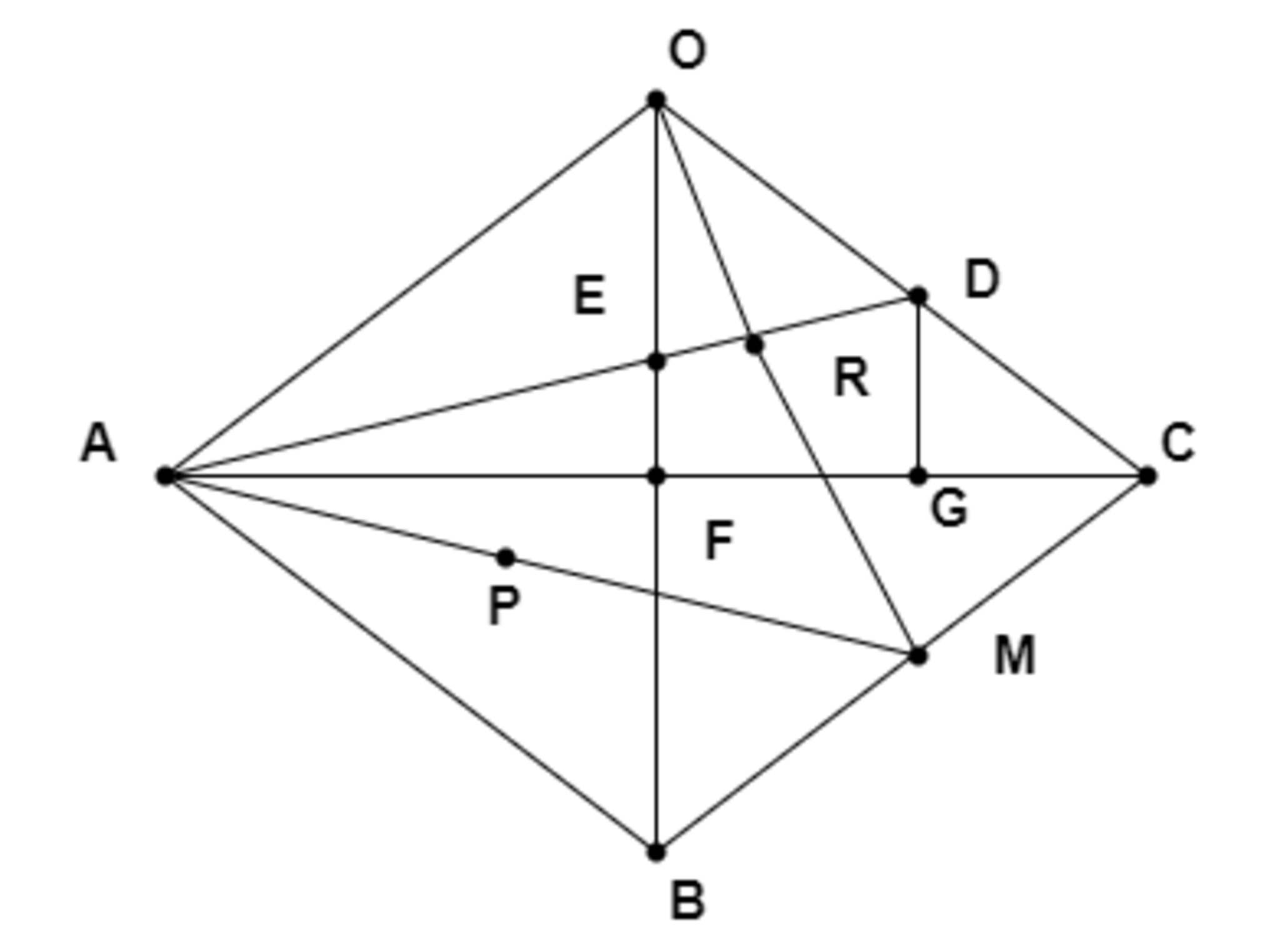大問6(2)
(線分OMなど一部の線が折れ線になってますが、直線だと思ってください)

線分ACと線分OBとの交点をF、点Dから線分ACへ下した垂線の足をGとします

□OABCはひし形なので、$AF = CF$
中点連結定理により
$CG : CF = DG : OF = 1 : 2$

$△AFE ∽ △AGD$より
$EF : DG = AF : AG = 2 : 3$

よって
$OE : EB = 2 : 4 = 1 : 2$
$△OED = △OBC × \frac{1}{2} × \frac{1}{3}$
$= \frac{1}{6}△OBC$ ...①

$OR : RM = x : y$とすると
$△OER = △OBC × \frac{1}{2} × \frac{x}{x+y} × \frac{1}{3}$
$= \frac{x}{6(x+y)}△OBC$

$△ODR = △OBC × \frac{1}{2} × \frac{1}{2} × \frac{x}{x+y}$
$= \frac{x}{4(x+y)}△OBC$

$△OED = △OER + △ODR$
$= \frac{x}{6(x+y)}△OBC + \frac{x}{4(x+y)}△OBC$
$= \frac{5}{12(x+y)}x△OBC$ ...➁
①, ➁より

$\frac{1}{6}△OBC = \frac{5}{12(x+y)}x△OBC$
$2(x+y) = 5x$
$3x = 2y$
$\frac{y}{x} = \frac{3}{2}$

よって
$OR : RM = 2 : 3$

➁

ここが正答率0%の設問です

とりあえず、簡単に求められる△PBCの面積を求めましょう
$△PBC = 12 × 6\sqrt{3} × \frac{1}{2} × \frac{5}{9}$
$= 20\sqrt{3}$ ...①

次に高さを求めましょう
まず点Qの居場所を見つけだします

四点O, A, P, Mは同一平面上(△OAM)に存在します

点Rと二点O, Mは一直線上にあるので、O, M, Rは同一平面上にあるといえます

また、点Qと二点O, Pは一直線上にあるので、O, P, Qは同一平面上にあるといえます

以上から、点Qは△OAMと△ADE上に存在することがわかります

よって、△OAMについて書くと、以下のようになります

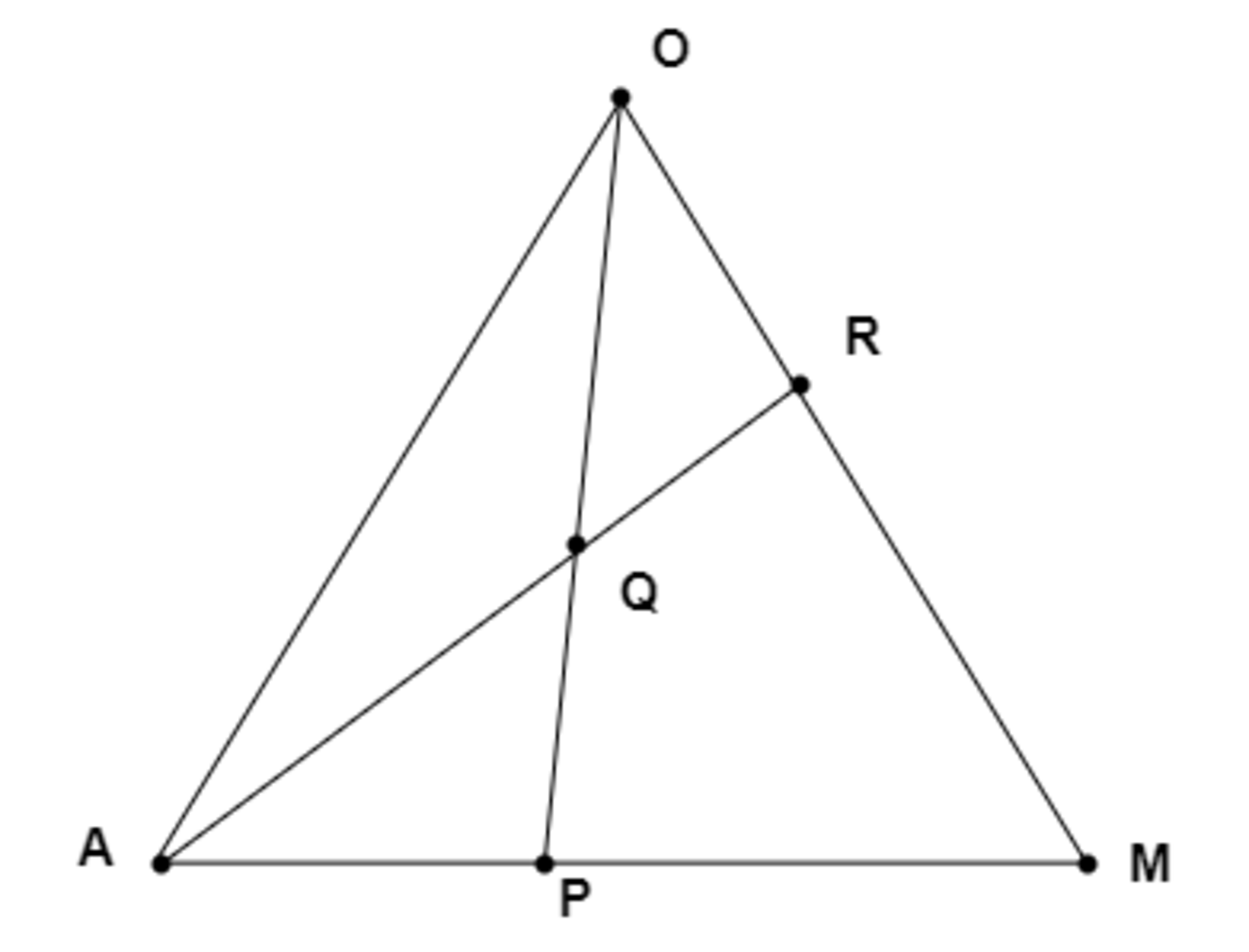大問7(3)1

ここで、点Rを通り線分OPに平行な直線と線分AMとの交点をSとします

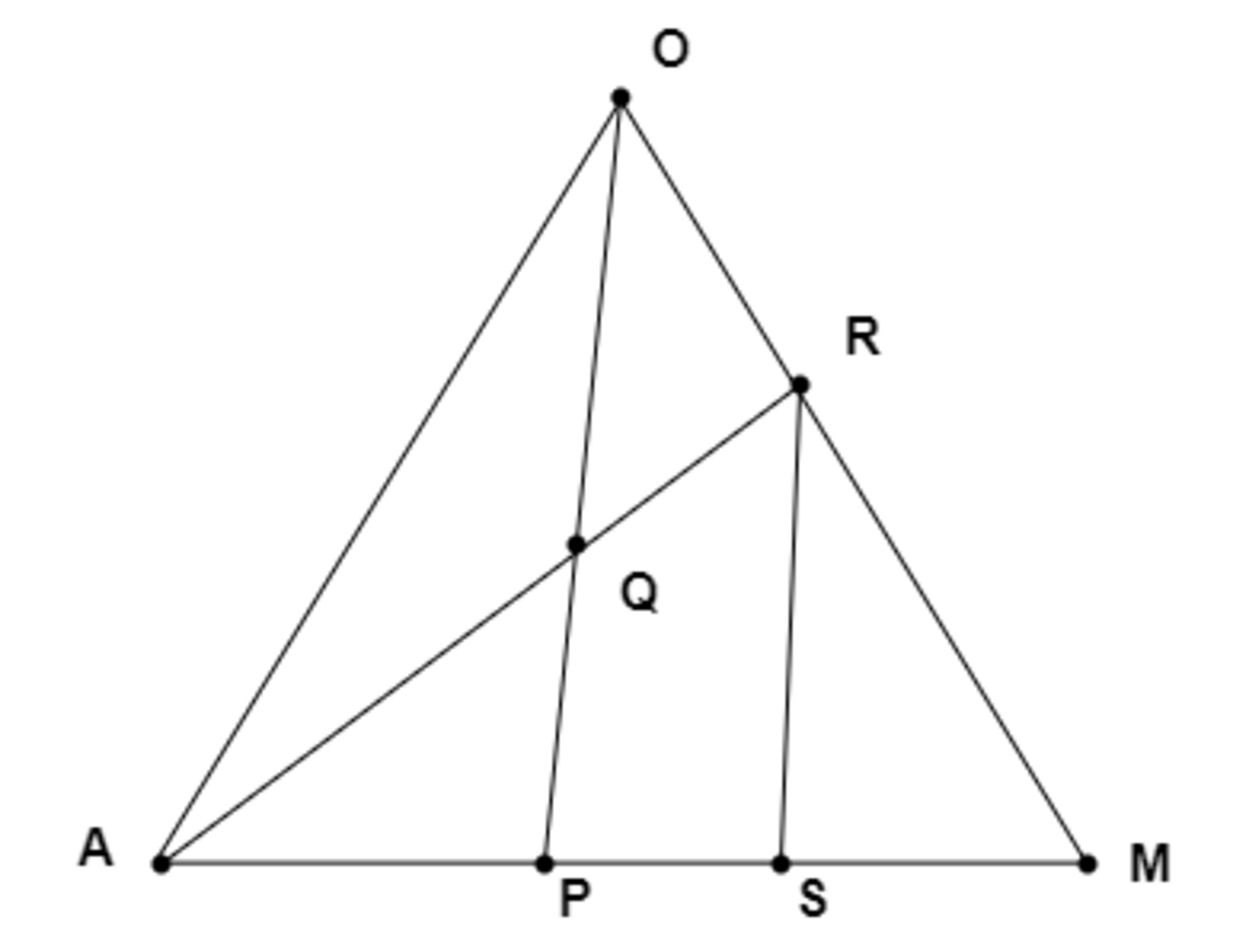大問7(3)2

$OR : RM = 2 : 3$
$△MRS ∽ △MOP$
$△APQ ∽ △ASR$
より

$MS : MP = RS : OP = 3 : 5$
$QP : RS = AP : AS = 4 : 6 = 2 : 3$
よって
$OQ : OP = 5 - 2 : 5 = 3 : 5$

さて、高さを求めていきましょう

点Mと線分OAとの距離を$h$、点Oと△ABCとの距離を$i$とします

$OM=AM$, 三平方の定理により
$h^2 + 6^2 = (6\sqrt{3})^2$
$h^2 = 6^2 × (3 - 1)$
$h^2 = 6^2 × 2$
$h = 6\sqrt{2}$

$6i\sqrt{3} × \frac{1}{2} = 12 × 6\sqrt{2} × \frac{1}{2}$
$i = 4\sqrt{6}$

よって、三角錐QPBCの高さは
$ 4\sqrt{6} × \frac{2}{5} $
$ = \frac{8\sqrt{6}}{5} $ ...②

①, ➁より、三角錐QPBCの体積は
$20\sqrt{3} × \frac{8\sqrt{6}}{5} × \frac{1}{3}$
$= 32\sqrt{2} (cm^3)$

感想

完走した感想ですが、この年は例年の福島県高校入試と比べたらかなり難しい年だったと思います
特に、大問5と7に関しては、高校数学の知識を使えば楽だけど、そんなの知らない人が大半だと思うので難しいかなーとは思いました
ラストの正答率が0%になったのも、時間的な問題や高さの比を求めるのが難しかったのかなといった印象(高さに関してはメネラウスの定理を使うことで若干楽になる)

ただ、福島県の高校入試数学は、令和になってからだいぶ簡単になってきていて、このレベルの問題はもう中々でないと思うので、福島の受験生のみんなは安心してね