トリリウムの定理で瞬殺せよ．
この記事は特に深掘りしていません．
目次
1.トリリウムの定理とは
2.問題（2問だけ）
3.問題2の解答
4.終わり
トリリウムの定理とは
ざっくりと言えば，内心と外接円，傍心を絡めた定理です．
$\triangle \mathrm{ABC}$において，内心$\mathrm I$，$\angle \mathrm A$の傍心を$\mathrm{I_A}$，外接円$\omega$と直線$\mathrm{AI}$の交点を$\mathrm D$とする．このとき，$4$点$\mathrm{I,B,C,I_A}$は点$\mathrm{D}$を中心とした同一円周上に存在する．尚，線分$\mathrm{I\;I_A}$は$\omega$の直径となる．
証明は こちら
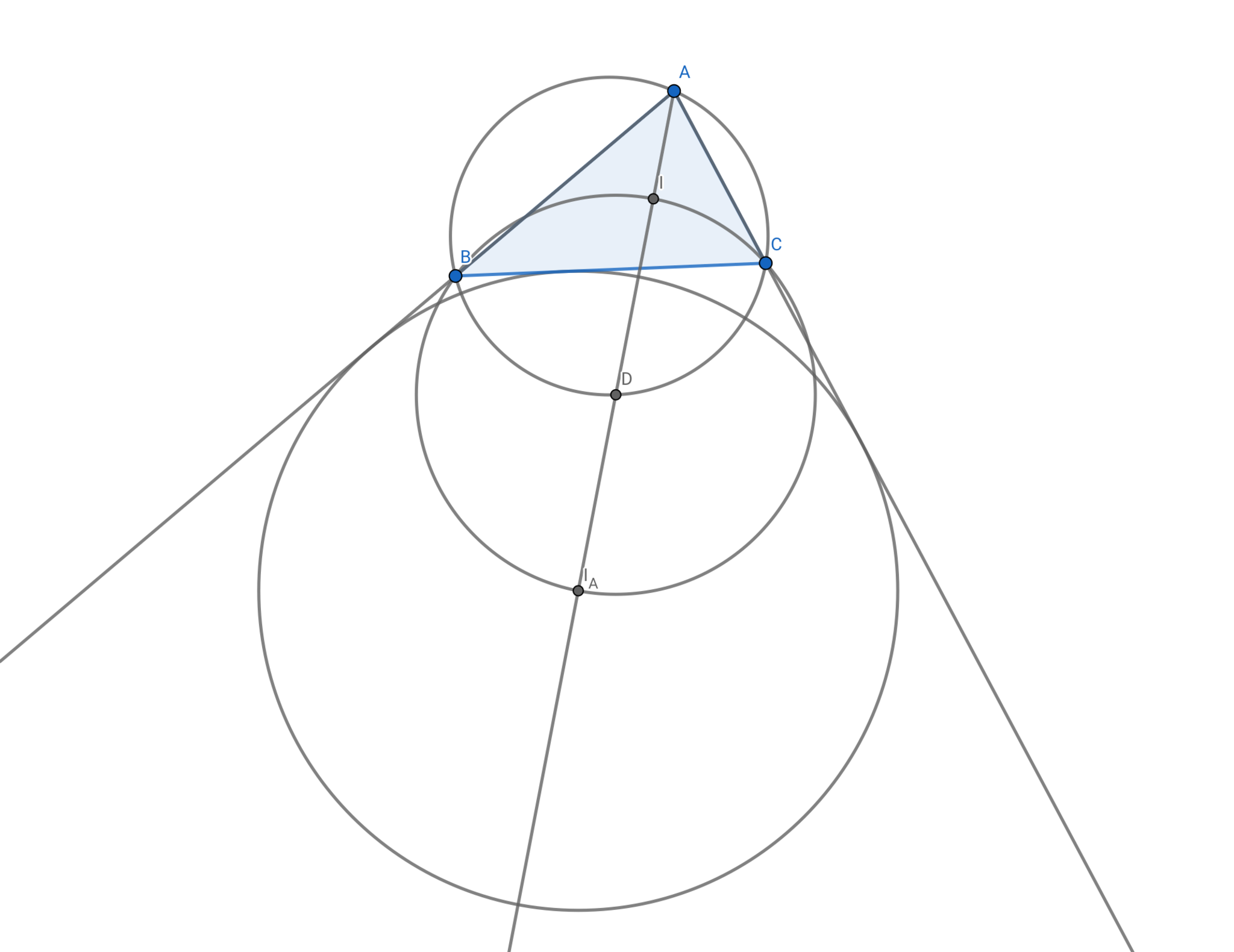トリリウムの定理
最初この定理を見たとき，こんな定理どこで使うんだよ！と思っていました．しかし，OMC132(F)で出題されてしまいました(泣)．まさかの4bで黄diffというすさまじい事態が起きてしまいました．これ以降，なぜかトリリウムの定理を知っている人たちが急増しました．
問題（2問だけ）
$5$点$A,B,C,D,E$はこの順で同一直線上に並んでおり，次を満たします．
$$AB=7,BC=3,CD=4,DE=6$$
平面上に相異なる$2 $点$F,G$をとると，$3$点 $E,F,G$は同一直線上になく，三角形$EFG $の内心は$D $になり，三角形$EFG$の外接円$\omega$は$B$を通りました．直線$AF $と$\omega$の交点のうち$F$でない方を$H$とします．$HC=8$のとき$FD^2$を求めて下さい．
ただし，答えは互いに素な正の整数$a,b$を用いて$\dfrac{a}{b}$と表されるので，$a+b $を解答して下さい．
解答は こちら
Let triangle $ABC$ satisfy $2BC = AB+AC$ and have incenter $I$ and circumcircle $\omega$. Let $D$ be the intersection of $AI$ and $\omega$ (with $A, D$ distinct). Prove that $I$ is the midpoint of $AD$.
この問題はそれなりの(？)解答を書こうと思います．問題文の解読は自力で頑張ってください．
問題2の解答
図は以下のよう．
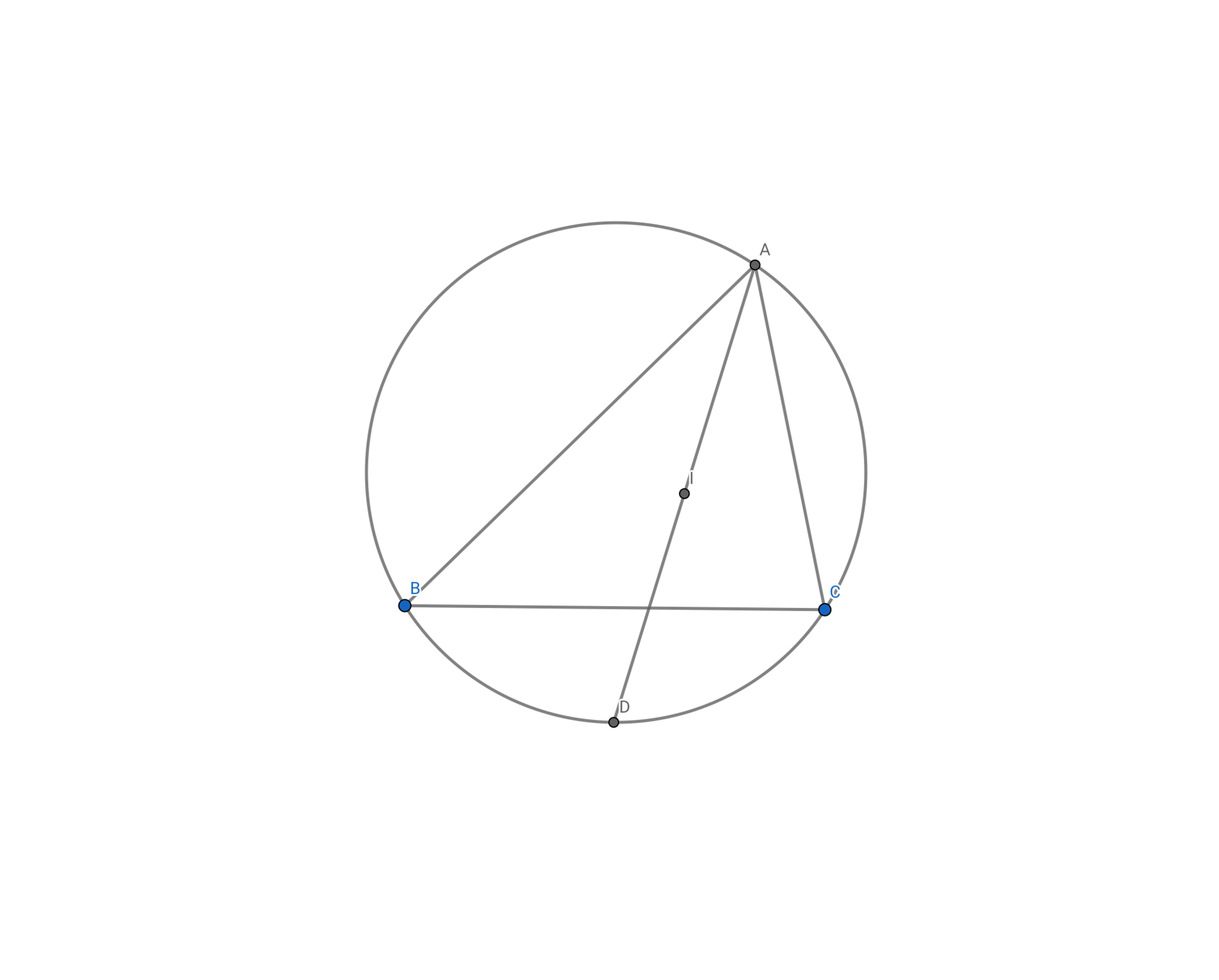問題2
$\angle \mathrm{A}$の傍心を$\mathrm {I_A}$とすると，トリリウムの定理より，$4$点$\mathrm{B,I,C,I_A}$は同一円周上に存在し，$\mathrm D$はその円の中心となる．
点を以下の図のようにおく．(図3)
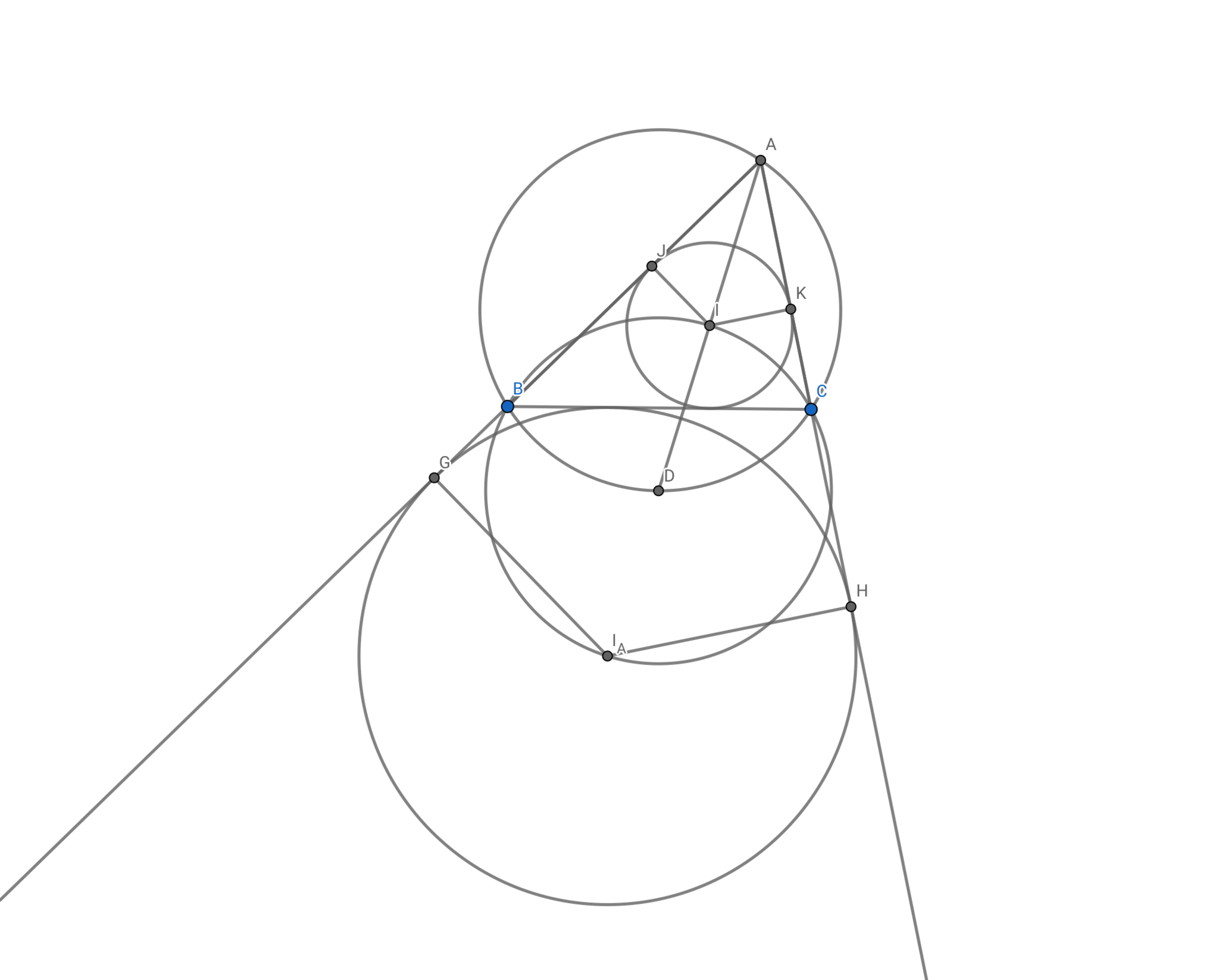問題2
$\aqr{AIK}$と$\aqr{AI_AH}$は相似であるので，$3\mathrm{AK}=\mathrm{AH}$を示せばよい．$\q{AK}=x,\q{AC}=x+y,\q{BC}=y+z,\q{BA}=z+x$となるように正実数$x,y,z$を定めると(Ravi変換)，問題文の条件から$y+z=2x$がわかる．よって，$\q{AH}=\frac{\q{AB+BC+CA}}{2}=\frac{2(x+y+z)}{2}=3x$がわかる．
よって$3\q{AK}=\q{AH}$となり，トリリウムの定理を踏まえると点$\q I$は線分$\q{AD}$の中点であることが示された．(証明終)
終わり
トリリウムの定理は忘れた頃にやってくる恐ろしい定理です(偏見)．ただ，知っていると一発なので覚えておくといいかもしれません．
余談なのですが，わざわざRavi変換する必要なかったですね🙂
