競技数学典型/難角問題
はじめに
今回は予選で頻出な難角問題について,ある程度太刀打ちできるようになったので思考方法を言語化してみます.僕は難角問題初心者なので至らない部分も多いと思いますが,よろしくお願いします.
本記事の作成にあたって, @tyenn7 さんには大変お世話になりました.ありがとうございます!
本記事に修正、加筆を加えた 最新版 もぜひご覧ください。
抑えるべきは一つだけ!
難角問題で意識すべきことはただ一つです.「隠れた特殊性を見つける」ということだけです.これを成し遂げるための手段として有名なものがいくつかあるので,以下で例を挙げて紹介していきます.
典型構図
正方形と合同
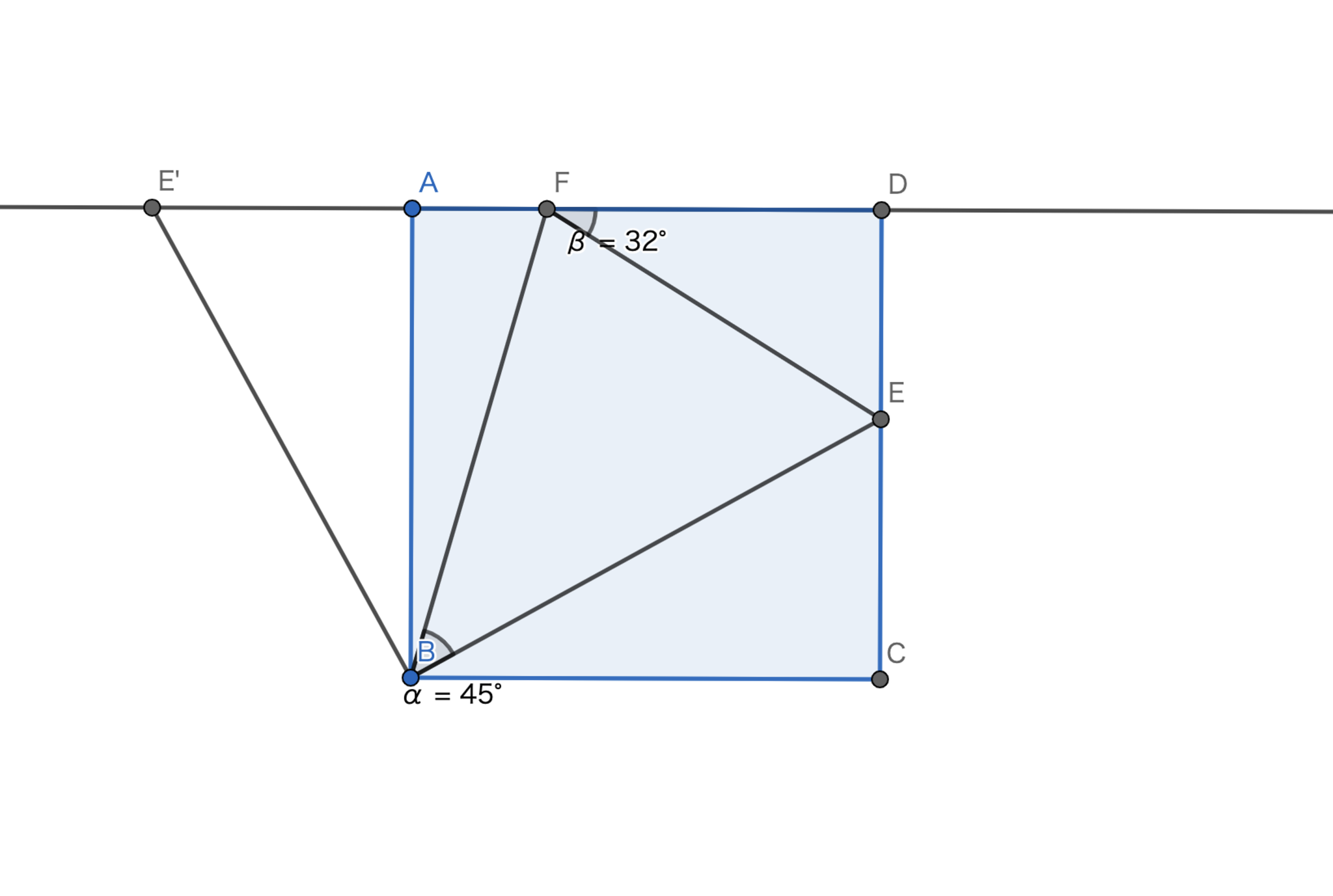
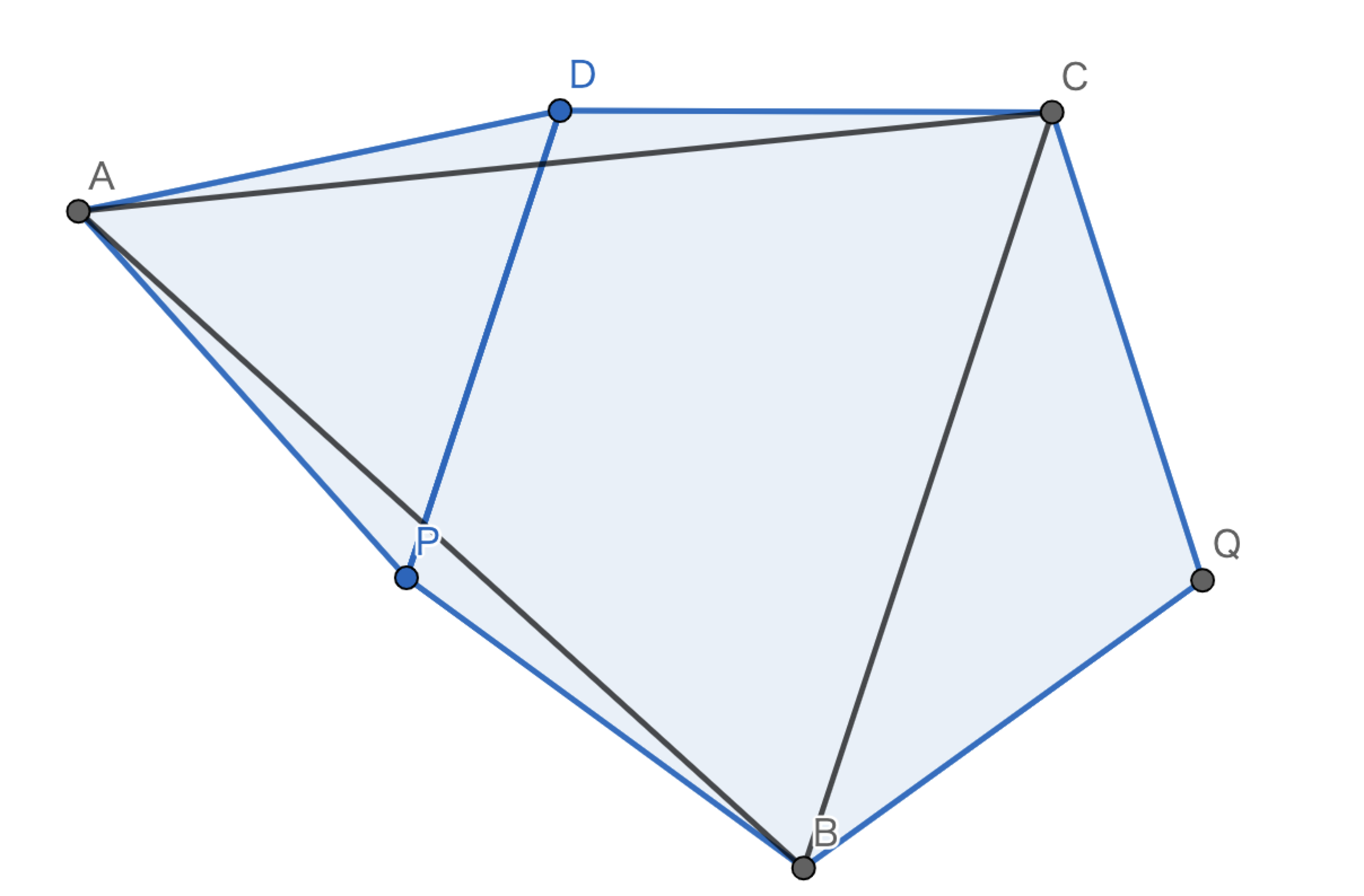
正方形$ABCD$の辺$CD,DA$上に点$E,F$が存在して$\angle{EBF=45°},\angle{DFE}=32°$を満たすとき$\angle{BEC}$の大きさを求めよ.
隠れた対称性を見つけるには与えられた条件をフルに使うことが大切です.特に,正方形という条件は強力で,さらに$45°$という条件が$90°$と関連していることも予想できます.
これらの条件をフルに使うならば,$EC=E'A$なる点を図のように取れば良いです.$\triangle{BE'F} \equiv \triangle{BEF}$であるので$\angle{FEB}=\angle{CEB}$が得られて$\angle{BEC}=61°$となる.
正方形型1
合同な三角形の構図
$\angle{ADB}=\angle{ADC}$を満たす以下のような状況がある時,$BD=PD$なる点$P$をとれば合同な三角形ができて嬉しいことがあるかもしれません.
合同の構図
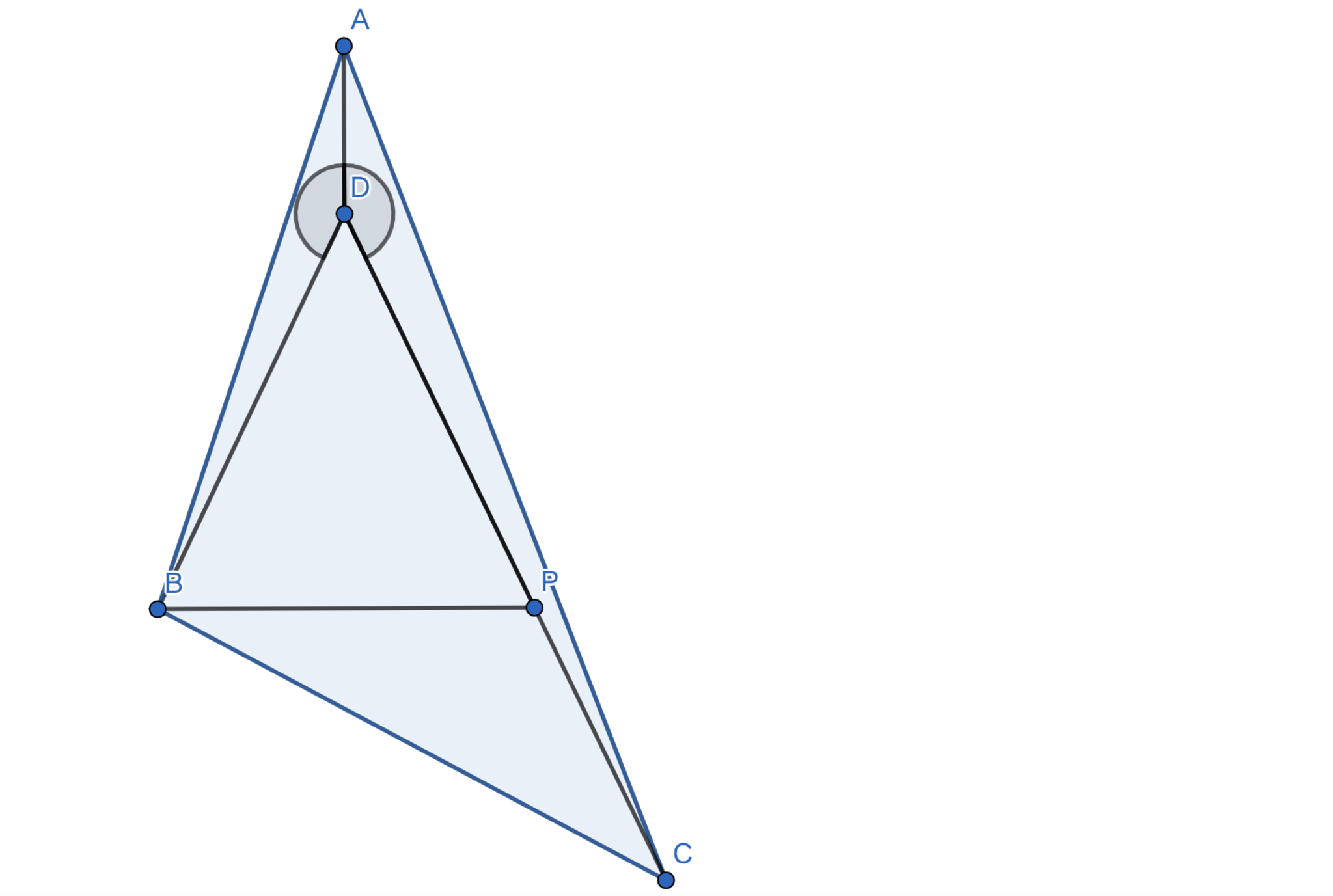
三角形${ABC}$の内部の点$P$は以下を満たす.
このとき，$\angle{PCA}$ を求めよ。
早速構図を適用してみましょう.簡単な角度計算をしてみると$\angle{APB}=\angle{APC}=130°$となるので$PB=PD$なる点$D$をとることを考えます.すると,$\angle{PDB}=40°$と併せて$\triangle{ABD}$が正三角形であるとわかります.さらに簡単な角度計算を行うことで$BD=CD$となるので$AD=CD$となり,$\angle{DCA}=10°$となります.
難角問題は初めからうまくいくことは読めないんです.対称性を駆使して隠れた条件を発見していくことが大事になります.
合同の構図-2
対称移動
全ての内角が$180°$未満である五角形$ABCDE$において以下が成立しました.
匂いますね.$\angle{BAE}=22°$で$\angle{CAD}=11°$はとっても怪しいです.これはすなわち$\angle{BAE}=2\angle{CAD}$であることを表しています.
さて,難角問題ではまず「対称移動」を考えましょう.これは本当に重要な定石です.隠れた特殊性を見つけるのにすごく役立つのが対称移動なのです.例に漏れず,今回もそうです.では,どこを対称移動すれば良いのでしょうか...？そうです!$\angle{BAE}=2\angle{CAD}$なので$B,E$を$AC,AD$に関して対称移動させると一致するのでその対称移動を考えましょう.この点を$P$とします.すると,$\triangle{PCD}$は条件より正三角形となります.$\angle{BCP}=31°,\angle{CPD}=60°$です.四角形$PEAB$に着目すると$\angle{BPE}=169°$となります.よって,$\angle{DPE}=56.5°$となります.従って,$\angle{CDE}=127°$となるわけです.気づけば一瞬ですね.
OMC108-D
作図可能性を考える
JJMOからの出題です.
$AB=AC$なる二等辺三角形の内部に点$P$をとったところ以下が成立した.この時,$\angle{PAC}$を求めよ.
難角問題は普通のangle-chaseでは情報が足りないことが多いです.大抵は特殊な"解ける"状況になっているのです.ということで,その隠された特殊性を探し当てることが重要になってきます. そこで役立つことがあるのが作図可能性です.
まずは図を描いてみましょう.綺麗に図を描きたいから見た目や直感ではなく,出来るだけ論理に基づいて作図してみましょう.$\angle{BAC}=70°$を丁寧に作図するのは難しいですが,$\angle{APC}=150°$なら論理的に作図可能ですね.円周角の定理を使いましょう.具体的には$OAC$が正三角形になるような点のうち,$P$でない側にあるものを点$O$としてみれば$O$を中心とする半径$OA(=OC)$の円上に存在することになります.良い情報が得られましたね.さらに,$AB=AC=AO$なので$\angle{ABO}=\angle{AOB}=\frac{180°-(70+60)}{2}=25°$とわかります.一方で$\angle{ABP}=25°$なので$B,P,O$は共線であるとわかります.なるほど!今回隠された特殊性はこれだったわけですね.あとはとってもシンプルです.円周角の定理より,$\angle{PAC}=\frac{\angle{POC}}{2}=\frac{35°}{2}$となるわけです.
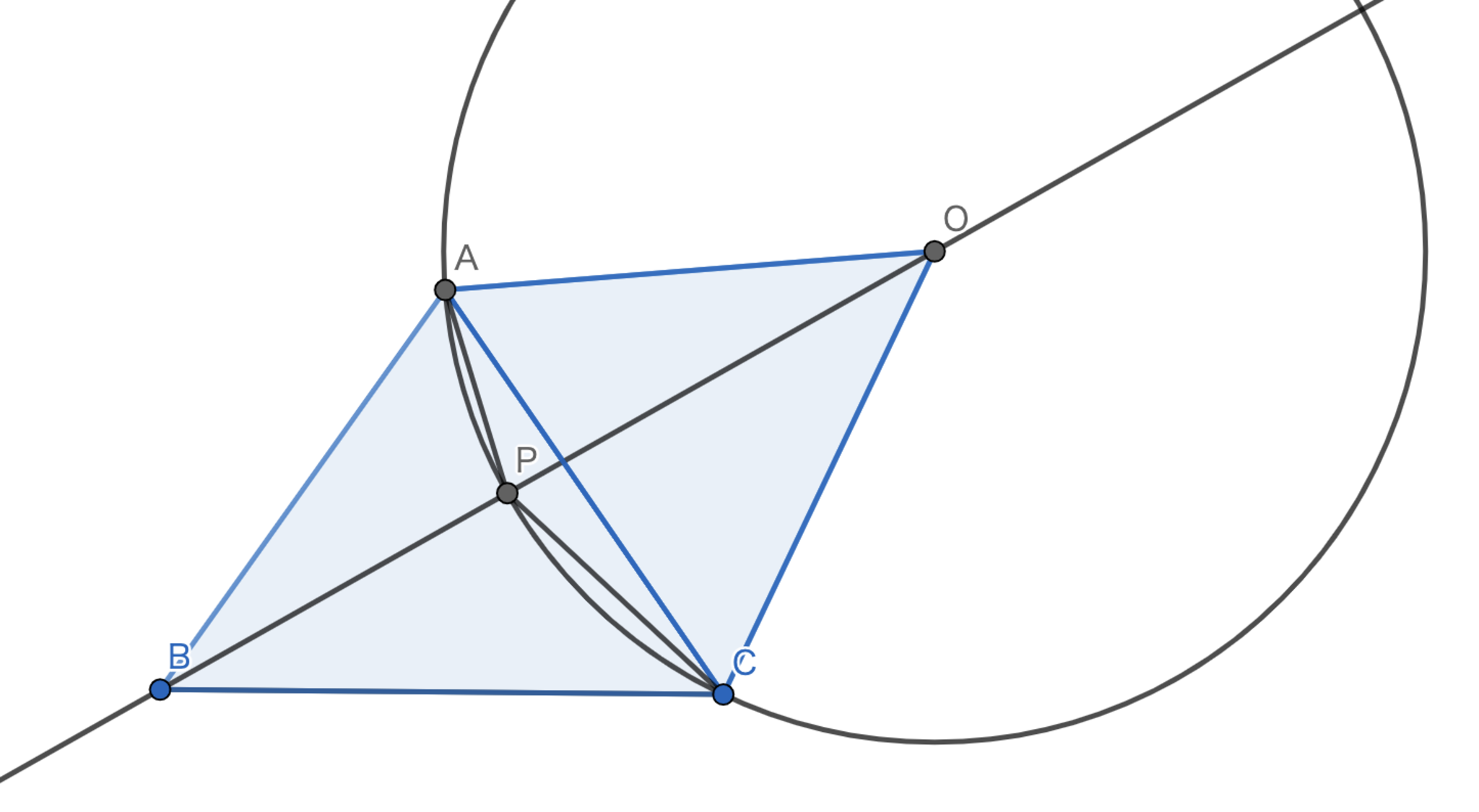JJMO2015-7
作図可能性から見抜く正多角形
今までは特殊性を見出そうとした結果正多角形を発見するといった流れでしたが,正多角形を作りに行くことも有効です.
正五角形$ABCDE$の内部の点$P$は以下を満たす.$\angle{PAC}$の大きさを求めよ.
さて、最初は丁寧に論理的に作図する方法を考えてみましょう.${6°}$をどのように作図するかですが,正五角形を利用できないか考えてみましょう.$6°$を一つの角に持つような二等辺三角形の一つに$6°,6°,168°$という三角形があります.$168°$を作図できれば$6°$を作図できることになりますね.さて,ここで気づきたいのですが$168=108+60$です.これが何を意味するかわかりますか...？そうですね.正三角形です.このことから,図のように点$F$を取ると$B,P,F$は共線となります.$\angle{PEA}=12°$という情報を使うと$\angle{FPE}-\angle{PFE}=54°$であるから$AE=PE=FE$であるとわかります.以上より$\angle{PAC}=\angle{PAE}-\angle{CAE}=84°-72°=12°$であるとわかります.
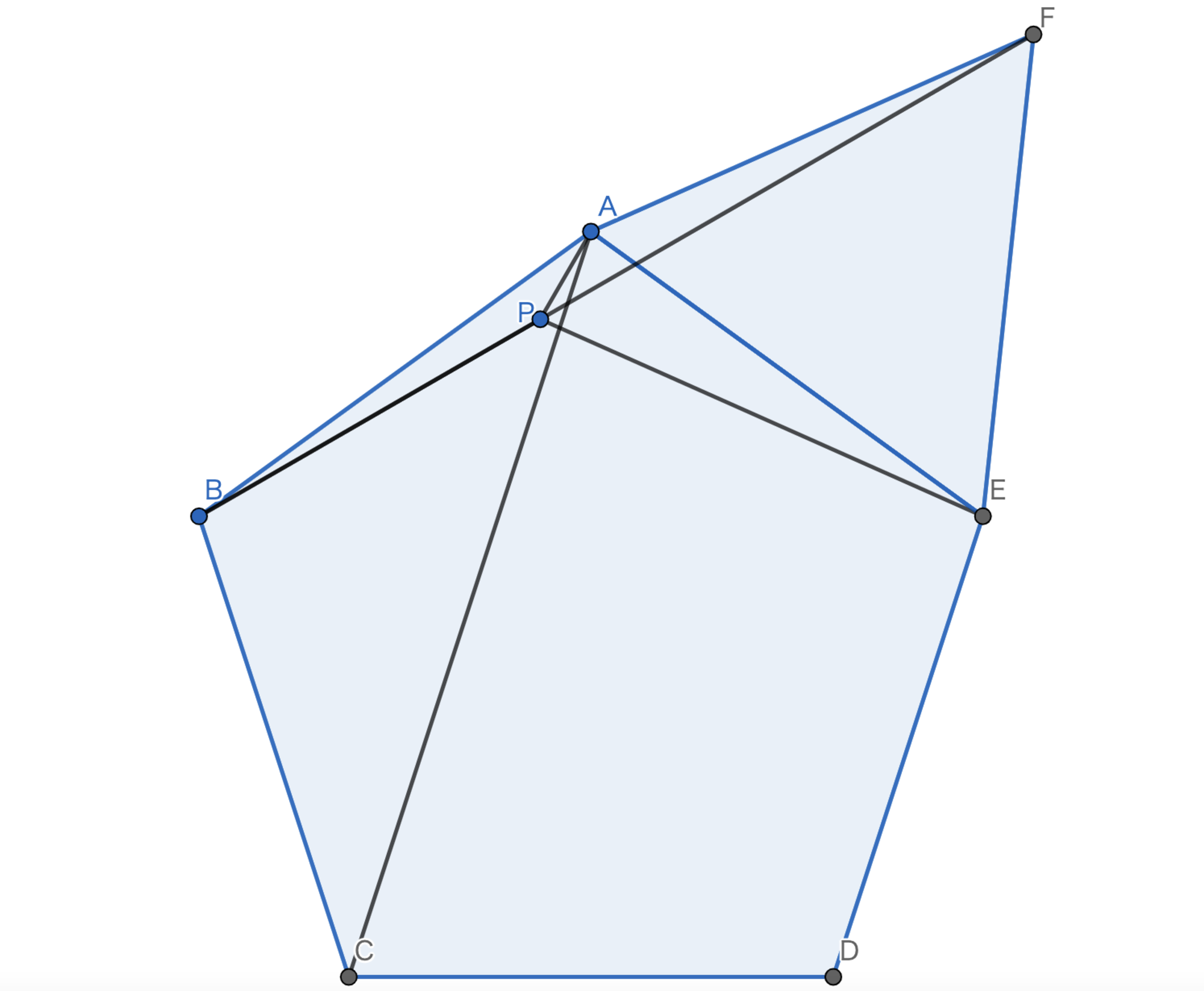JMO2005-9
演習問題
さて,ここからが本番です.できるかぎり多くのパターンの問題を演習問題として用意しました.難角問題は経験が一番です!全ての問題に発想法と解説を用意してあります.是非ご活用ください.
正方形$ABCD$の辺$CD,DA$上に点$E,F$が存在して$\angle{EBF=45°},\angle{DFE}=x°$を満たすとき$\angle{BEC}$の大きさを$x$を用いて表せ.
解答
この問題は「正方形と合同」の構図の一般化になっています。回答は$(45+\frac{X}{2})°$となります。
平行四辺形$ABCD$は$\angle{DBC}=15°,\angle{ACB}=30°$を満たす.この時,$\angle{BAC}$の大きさを求めよ.
解答
この問題の主な発想は「特殊角から正多角形を利用しよう」というものになります.
$AC$の中点を$M$,$A$から$BC$へと下ろした垂線を$E$とします.この時$\triangle{EMA}$は正三角形なので$\angle{BME}=15°$とわかります.従って$BE=EM=MA=AE$であり,$\angle{BAC}=45°+60°=105°$となります.
正五角形$ABCDE$の内部の点$P$が以下を満たした.このとき,$\angle{BDP}$の大きさを求めよ.
解答
この問題の発想は「作図可能性から見抜く正多角形」になります.
$\angle{EAP}=54°$であることから$P$は$BE$の垂直二等分線上に存在することになり,$\angle{BPA}=84°$なので$\angle{CBP}=66°$となります.$\triangle{QCD}$が正三角形となるように正五角形の内部に点$Q$を取ると,簡単な角度計算より$\angle{CBQ}=66°$となります.$P,Q$は共に$BE$の垂直二等分線上にあり,$\angle{CBP}=\angle{CBQ}$であるから$P=Q$を得ます.$\angle{BDP}=60°-36°=24°$です.
(これは一見天下り的かもしれませんが,正確に作図するには?を考えると見抜くことができます.)
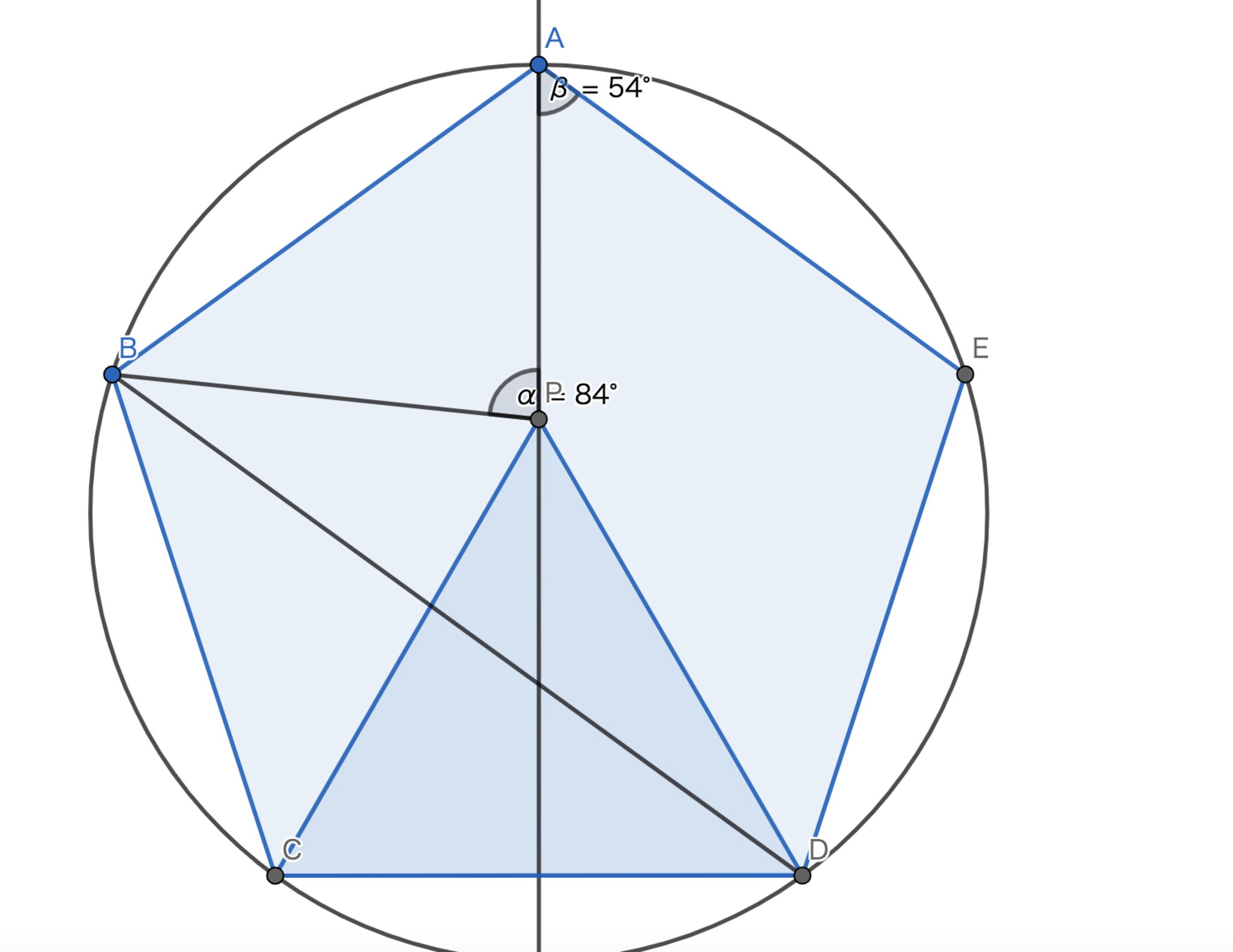問題8
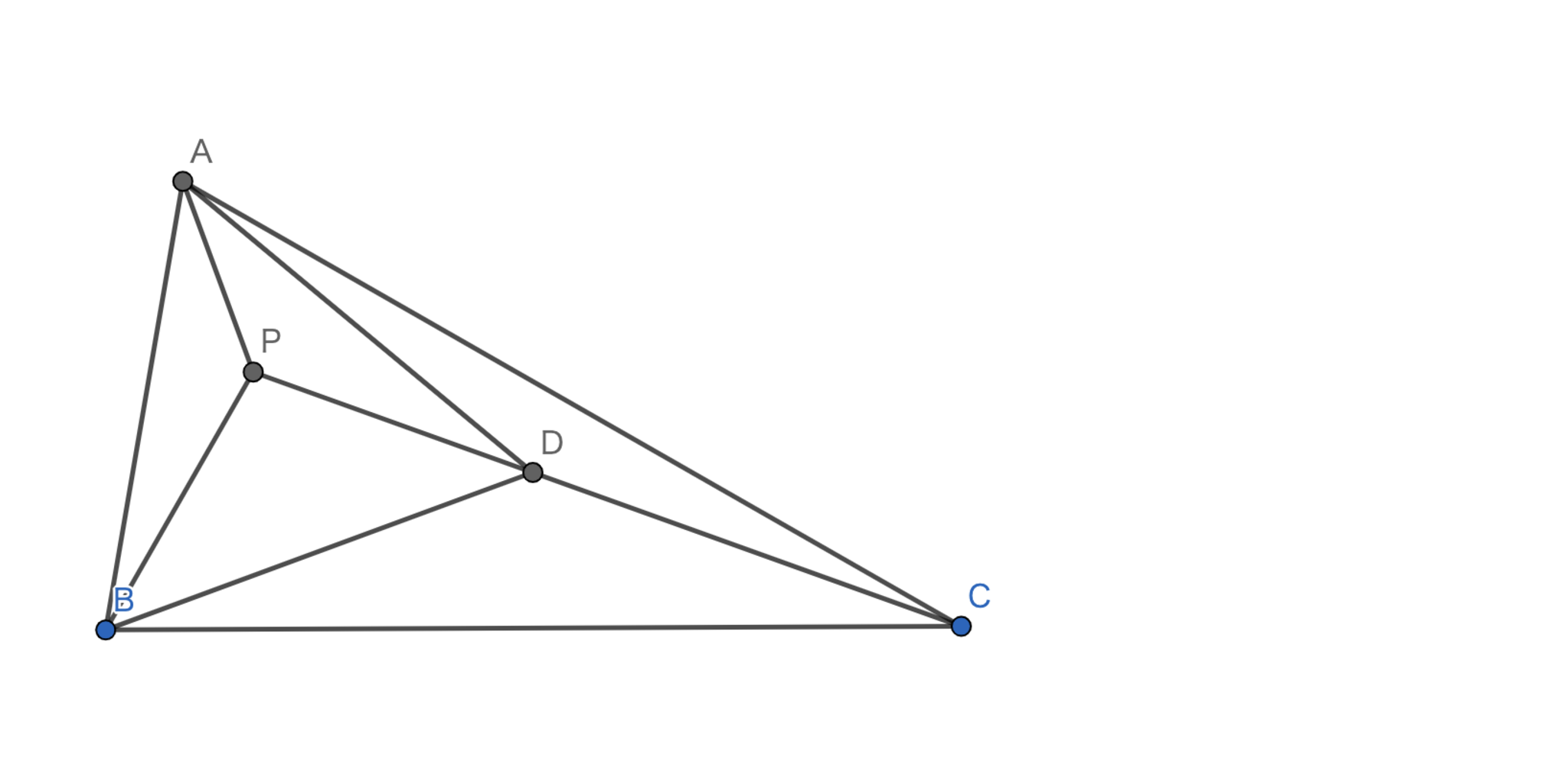
三角形$ABC$の内部の点$P$が以下を満たす.$\angle{PBC}$の大きさを求めよ.
出典元のツイートは
こちら
解答
この問題の発想は等しい角度がたくさん登場していることから「合同な三角形の構図」を連想したくなるところにあります.
実際に,この問題は比較的見えやすいと思います.半直線$AB$上に$PB=QB$となる点$Q$をとれば$\triangle{PQC}$が正三角形となります.さらに$\triangle{PBC}\equiv \triangle{QBC}$となるので$\angle{PBC}=74°$となります.
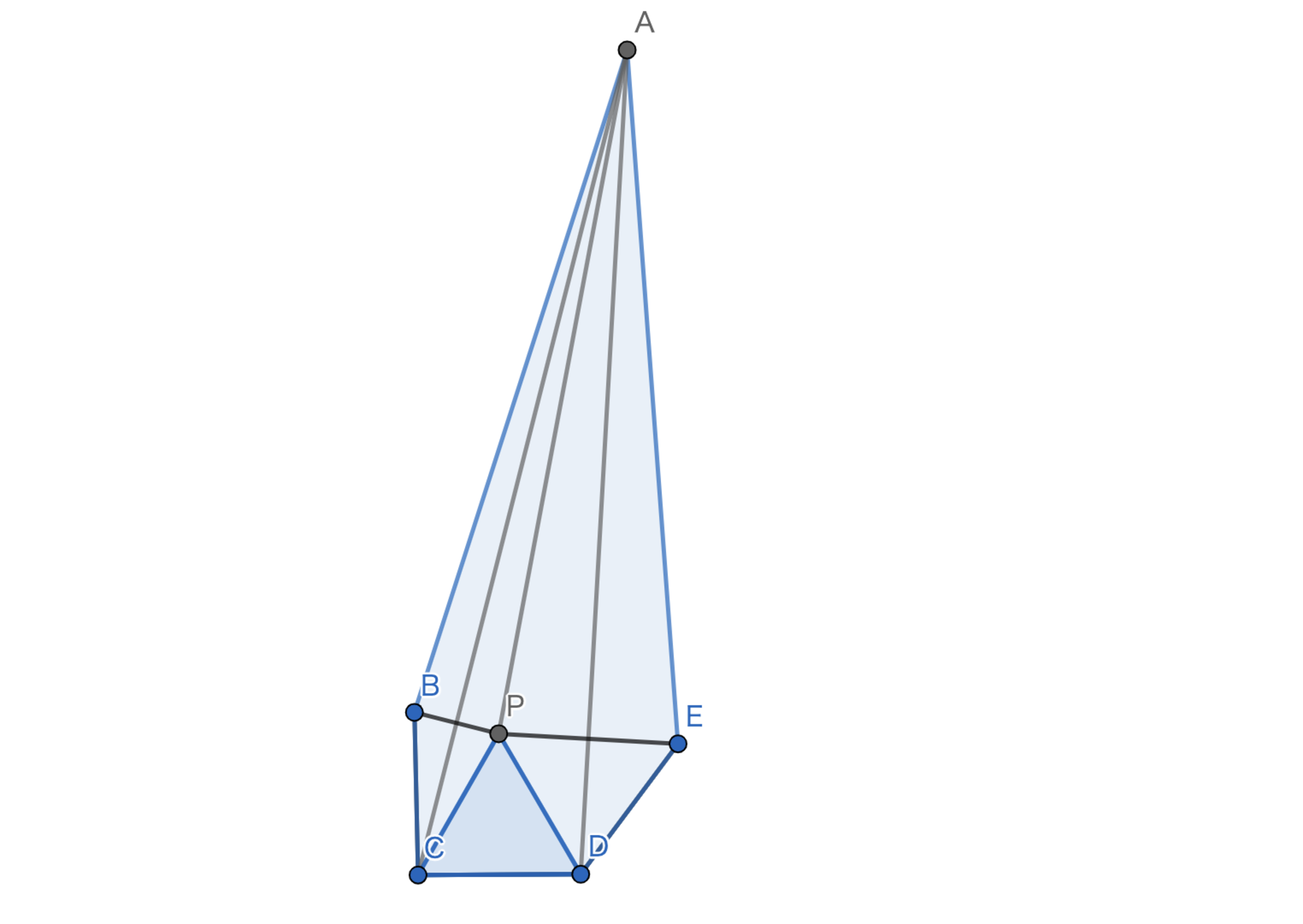
三角形$ABC$の内部の点$P$が以下を満たす.$\angle{PBC}$の大きさを求めよ.
出典元のツイートは こちら
解答
この問題の発想は「合同の構図」を作ることです.
この問題では典型構図を使った後に発想力にあまり頼らない解法で解いてみようと思います.まずは,合同の構図を見抜きましょう.$AP$上に$AQ=CQ$となる点$Q$を取ります.すると,簡単な角度計算により$PQ=PC$がわかり,合同な三角形が見つかるので$BQ=BC$となるわけです.ここでしばらく図を眺めていると$\triangle{BCQ}$は正三角形なのではないだろうかと予想がたちます.従って,それを示していきたいのですがここで少しゴリ押しチックな方法を使ってみましょう.
仮に$\angle{ABQ} > 9°$であると仮定してみましょう.すると,$\triangle{AQB}$の角度の大小関係から$AQ > BQ$であるとわかります.一方で,$\triangle{BCQ}$の角度の大小関係から$BQ > CQ$であるとわかります.$AQ > BQ > CQ = AQ$が成り立ってしまうことになって矛盾します.よって,$\angle{ABQ} \le 9°$であるとわかります.同様にして,$\angle{ABQ} \ge 9°$であるので$\angle{ABQ} = 9°$です.よって,$\angle{PBQ} = 30°$です.いやぁ,素晴らしい問題ですね.
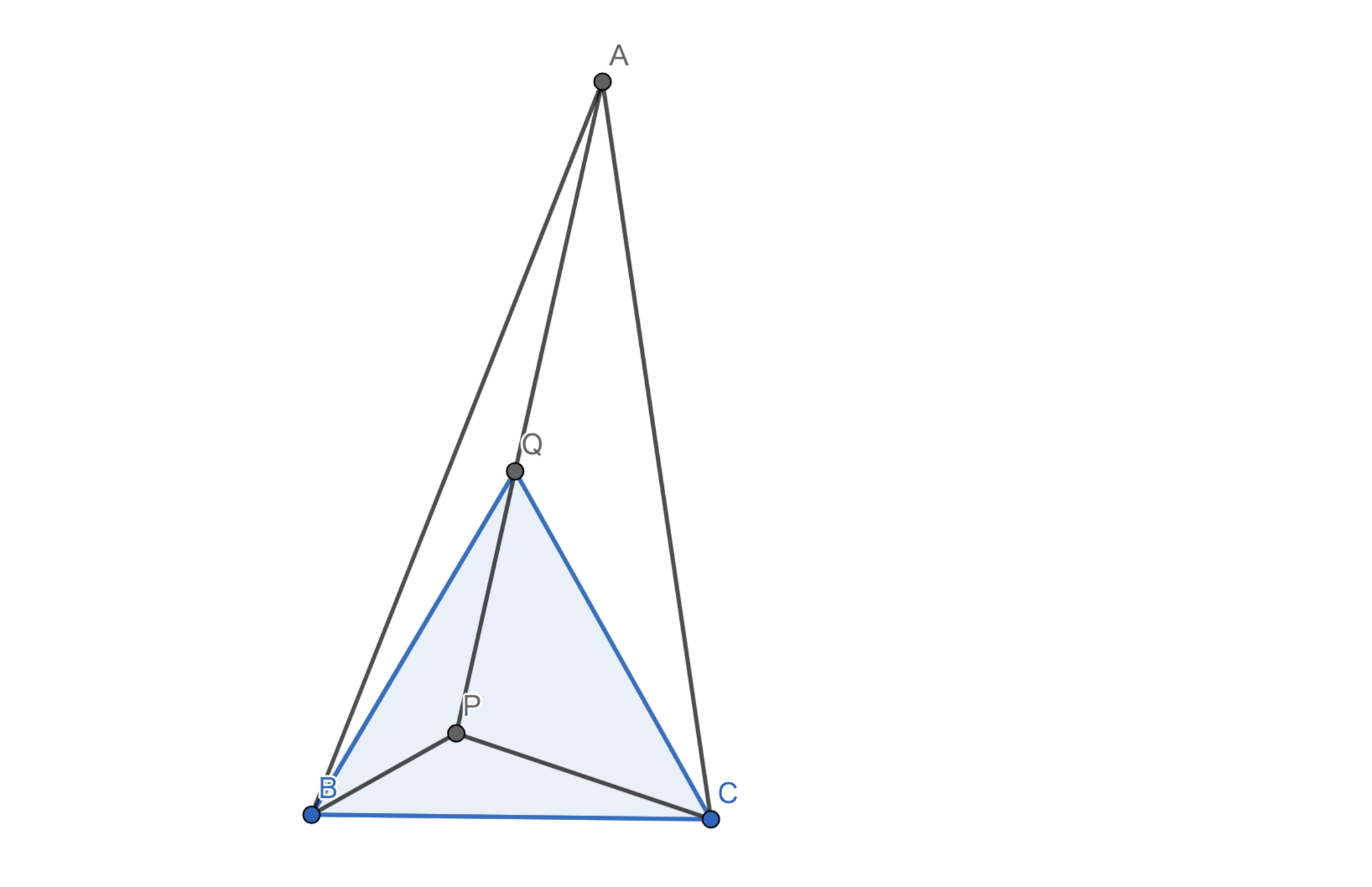問題10
三角形$ABC$および内部の点$P$が以下の条件を満たします。$\angle{PAC}$の大きさを求めてください。
凸四角形$ABCD$は$AD=CD, \ BD=BC, \ \angle{ADC}=168°, \ \angle{ABC}=66°$を満たす.この時,$\angle{BAD}$の大きさを求めよ.
解いてみた
なんとなくやりたくなったのでやってみます.「$168=108+60$なので正三角形+正五角形かな...？」
〜とりあえず図を書く〜
「なんか解きにくそうだなぁ」
「$\dfrac{180-168}{2}=6$を使うのかな...？」
「とりあえず,$AD$を一辺とする正三角形を作図してみる.」
「ん？これって四角形の内部に収まらないのかな...?」
「お、丁寧に作図するとギリギリ外部にはみ出そう」
「隠れた特殊性は,正五角形の頂点と,Bが一致するとかどうなんだろう」
「これで矛盾がないので,いったんこれが正しいことを示す方針でいこう」
→「解けた!」
11番にしては弱い問題でしたね.
解答
発想は$168=108+60$なので「正多角形が関連している」ことを考えるというものです.図のように$AB$を一辺とする正三角形のもう一つの頂点を点$P$とします.同様に$B'PDCQ$が正五角形となるように点$Q,B'$を定めます.
$B$は$CD$の垂直二等分線上にあります.よって,$B'=B$とすると,$AC=AB,AD=AP,CD=CP$であるから,$\angle{PBA}=6°$となって,$\angle{ABC}=66°$となります.$B$が$B'$よりも直線$AC$に近い場合は$\angle{ABC} > 66°$となるので不適です.同様に$B'$が$B$よりも直線$AC$に近い場合は$\angle{ABC} < 66°$となるので不適です.よって,$B=B'$です.このことから,$\angle{BAD}=54°$となります.
JMO2004-11
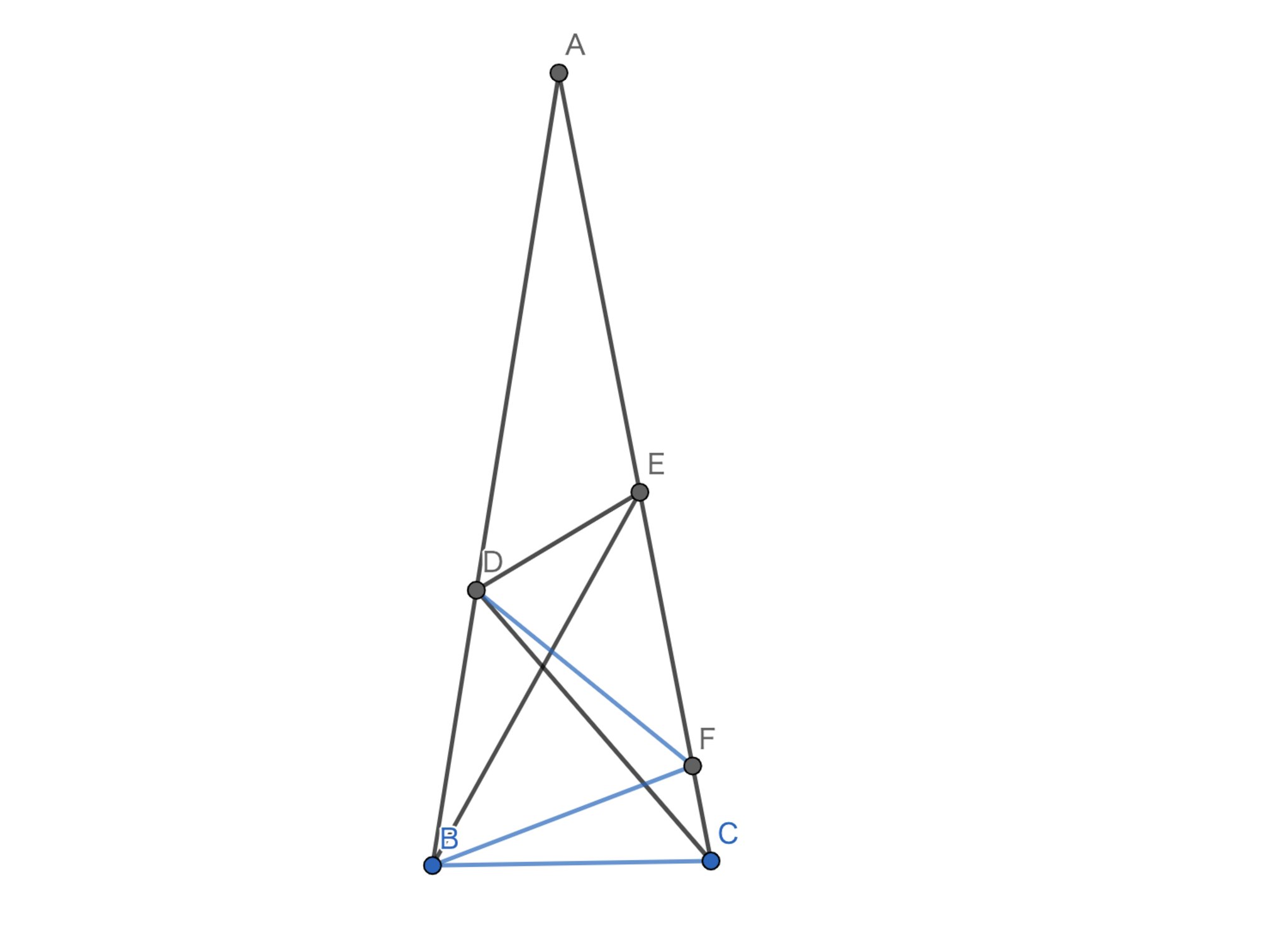
$AB=AC,\angle{BAC}=20°$なる二等辺三角形$ABC$の辺$AB,AC$上に点$D,E$をとったところ以下が成り立った.$\angle{BED}$の大きさを求めよ.
解答
ここまできたみなさんならば伝説の難問と言われたラングレー問題も簡単に解けると思います.
この問題の発想は,いい感じの角度と,辺の関係があるので「正三角形を作る」です.
簡単な角度計算により,$BC=BD$であるとわかります.$\angle{BEC}=40°$であることから$\angle{EBF}=40°$となるような$F$をとれば$60°$を絡めることもできてかなり嬉しい状況になることが想像できます.よって,$F$を取り角度計算を進めていくと,$BD=DF=BF=BC=FE$となり,$\triangle{FDE}$が二等辺三角形であることがわかるので$\angle{DEB}=30°$を得ます.
余談ですが,この問題が1972年の灘中入試で出題されたようです.結構すごいことしますねw
ラングレー問題