組み合わせ典型(主客転倒, 包除原理, 二項係数etc)
はじめに
この記事は Advent Math Calendar2022 の $25$ 日目の記事として書かれました.
組み合わせ問題の典型をいくつかピックアップし, 問題を交えながら解説する記事となっています.
その典型を全く知らない方から, ある程度典型を知っている方まで楽しめるような内容を心掛けました.
また, 組み合わせ典型と言いつつ, 実際には代数や整数分野であるような問題/内容も扱っています.
この記事には初出問題がいくつかあります.
記事の地の文内で解説している問題もあるため, 先に問題だけチャレンジしたいという方は
問題だけを抜き出して記事を用意したのでそちらを参照してください.
AMC day25の問題だけ
また, コンテスト形式で問題を解きたい!! という方は問題の中から抽出した $6$ 問を Google Formで解答できる場
(こちら)
を設けたのでそちらもチャレンジしてみてください.
目次
- はじめに
- 目次
- 主客転倒
- 包除原理
- 対称性
- 二項係数
- おわりに
主客転倒・寄与ゲー
続いては主客転倒や寄与ゲーと呼ばれるテクニックを紹介します.
これらは若干ニュアンスの違うような気もしますが本質は同じなのでまとめて扱います.
これらの考え方を一言でまとめると, 視点を変える となります.
これだけ言っても何の事やらだと思うのでまずは例題を見てみましょう.
$$\sum_{i=1}^{1000}\sum_{j=1}^{1000}\frac{1}{1000-|i-j|}$$
を計算してください.
この問題はシグマの中身だけをちょろっといじってみても和が計算しやすい形にはなりそうにありません.
そこで, 視点を変える主客転倒の考えが活きてきます.
まずこの問題が素直にシグマ内の式変形で解けそうにない原因を考えてみましょう.
(ある方法が上手くいかない原因をはっきりさせるとその後の考察がスムーズにいくというのは全分野共通事項な気がします.)
まず最初の素直な希望として, 内側のシグマだけ計算できないかを考えます.
ちょっと試してると, 分母の異なる分数を足し上げるのが困難そうです. 望遠鏡和のようなテクもダイレクトには効きそうにないです.
ここで考えるのが視点を変えるということです.
それは, "分母の異なる分数を足し上げるのが大変なら分母が等しい数たちをまず足し合わせればよいのでは??" という発想です.
分母が等しい数たちを先に足す方針を考えてみましょう.
以下の表は, $i,j$ の値と $|i-j|$ の値の対応表です.
| ↓$i$↓ →$j$→ | 1 | 2 | 3 | 4 | 5 | 6 | $\dots$ | 1000 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | $\dots$ | 999 |
| 2 | 1 | 0 | 1 | 2 | 3 | 4 | $\dots$ | 998 |
| 3 | 2 | 1 | 0 | 1 | 2 | 3 | $\dots$ | 997 |
| 4 | 3 | 2 | 1 | 0 | 1 | 2 | $\dots$ | 996 |
| 5 | 4 | 3 | 2 | 1 | 0 | 1 | $\dots$ | 995 |
| 6 | 5 | 4 | 3 | 2 | 1 | 0 | $\dots$ | 994 |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ |
| 1000 | 999 | 998 | 997 | 996 | 995 | 994 | $\dots$ | 0 |
これをみると, 斜めに同じ値が並んでいることが分かります.
この$1000\times1000$ の表で, 各値が何回登場するか数えてみましょう.
$0$ は対角線上に並び, その登場回数は $1000$ 回です.
$1$ は2本の斜め線上に並び, その登場回数は $2\times 999$ 回です.
$2$ は2本の斜め線上に並び, その登場回数は $2\times 998$ 回です.
$\vdots$
$k\ (k=1,2,\dots,999)$ は2本の斜め線上に並び, その登場回数は $2\times (1000-k)$ 回です.
$\vdots$
$998$ は2本の斜め線上に並び, その登場回数は $2\times 2$ 回です.
$999$ は2本の斜め線上に並び, その登場回数は $2\times 1$ 回です.
さて, 問題文の式
$$\sum_{i=1}^{1000}\sum_{j=1}^{1000}\frac{1}{1000-|i-j|}$$
を今数え上げた $|i-j|$ の値毎に足してみましょう.
$\begin{aligned} &\sum_{i=1}^{1000}\sum_{j=1}^{1000}\frac{1}{1000-|i-j|}\\ &=\sum_{k=0}^{999}\frac{1}{1000-k}\times(|i-j|=k \text{の登場回数})\ \ \ \ \ \ \ \\ &=\underbrace{\frac{1000}{1000}}_{k=0の分}+\underbrace{\sum_{k=1}^{999}\frac{2\times(1000-k)}{1000-k}}_{k=1,2,\dots,999の分}\\ &=1+\sum_{k=1}^{999}2\\ &=\mathbf{1999} \end{aligned}$
あら不思議, 複雑そうな式がするすると計算できてしまいました.
今回の解法を振り返ると,
- $i,j$ 毎に足すと上手くいかない(表の横や縦方向に足す)
- $|i-j|$ 毎に上手く足すと上手くいく(表の斜め方向に足す)
でした. このように, 問題文で与えられたそのままを扱うと困難なものをまさに別の角度から解きなおすというのが主客転倒の考え方の肝となります.
もう一問例を見てみましょう.
正整数 $n$ に対し, $10000$ を $n$ で割った余りを $M(n)$, $n$ の正の約数の総和を $S(n)$ とします.
$\sum_{n=1}^{10000}(M(n)+S(n))$ を求めてください.
やや恣意的に作られた問題なので折り畳みでヒントを置いておきます.
ヒント
$n$ の各約数 $d$ の寄与が分かるように, $S(n)$ を計算できるような表を書いてみましょう.
$n$ 毎に $M(n)+S(n)$ を計算したり, $M(n),\ S(n)$ のみの和を取ったりしても中々綺麗にはいきません.
これも表を書いて視点を変えるという事をしましょう.
下の表は各 $n$ が各 $m$ を割り切るなら $m$ を, 割り切らないなら $0$ を書いたものです.
| ↓$m$↓ →$n$→ | 1 | 2 | 3 | 4 | 5 | 6 | $\dots$ | 10000 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | $\dots$ | 1 |
| 2 | 0 | 2 | 0 | 2 | 0 | 2 | $\dots$ | 2 |
| 3 | 0 | 0 | 3 | 0 | 0 | 3 | $\dots$ | 0 |
| 4 | 0 | 0 | 0 | 4 | 0 | 0 | $\dots$ | 4 |
| 5 | 0 | 0 | 0 | 0 | 5 | 0 | $\dots$ | 5 |
| 6 | 0 | 0 | 0 | 0 | 0 | 6 | $\dots$ | 0 |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ |
| 10000 | 0 | 0 | 0 | 0 | 0 | 0 | $\dots$ | 10000 |
この表を縦方向に足し合わせて見ると, $n$ を割り切る $m$ の値が足しあわされている事が分かります. すなわち, 縦に足した和は $S(n)$ です.
特に, 表の数字を全て足し合わせると, $\sum_{n=1}^{10000}S(n)$ となります.
視点を変えます.
今度は, 表を横方向に足してみましょう.
各 $m$ は, $10000$ 以下の $m$ の倍数の個数分だけ足されます.
$10000$ 以下の $m$ の倍数は $\left\lfloor\dfrac{10000}{m}\right\rfloor=\dfrac{10000-M(m)}{m}$ 個ですので, 横方向に足し合わせると総和は $10000-M(m)$ となります.
特に, 表の数字を全て足し合わせると, $\sum_{m=1}^{10000}(10000-M(m))=10^{8}-\sum_{m=1}^{10000}M(m)$ となります.
表を横に足してから縦に足した値と, 縦に足してから横に足した値は等しいので,
$$\sum_{n=1}^{10000}S(n)=10^{8}-\sum_{m=1}^{10000}M(m)$$
です.
従って, 求める答えは, $10^{8}$ となります.
この問題も, $2$通りの角度から足した結果が等しいことを利用しています.
この章の最後に演習問題として, OMCで実際に出題された問題を紹介します.
足し合わせる方向を変えるという事を意識して考えてみてください.
$272$ 項からなる整数列 $\{a_i\}_{i=1,\ldots,272}$ のスコアを以下で定めます.
$$\sum_{i=1}^{256} |a_i-a_{i+16}|$$
$1,2,\ldots,272$ を並べ替えてできる整数列は $272!$ 通り考えられますが, それらのスコアの平均値を求めてください.
ただし, この平均値は整数値になることが証明できます.
問題へのリンク
ヒント
問題文の素直に解釈すると, 各数列に対して$256$個の値の総和を求める→全ての数列に対してスコアの総和を求める
という流れになります. 足す順番を変えましょう.
正整数 $N$ が増加的であるとは，$N$ を $10$ 進法で表記した際に各位の数が上位から狭義単調増加となることをいいます．例えば，$157$ や $5$ は増加的ですが，$804$ や $421$ や $334$ は増加的ではありません．
増加的な正整数は有限個しか存在しません．それらすべてについて総和を求めてください．
問題へのリンク
包除原理
この章では包除原理を説明します.
包除原理が適用されやすいのは, 「条件$P$ または条件$Q$ または条件$R$ または$\cdots$」 を満たすような要素の数え上げです.
まずは簡単な条件が $2$ つの場合を考えてみましょう.
$120$ 以下の正整数のうち, $2$ の倍数または $3$ の倍数であるものはいくつありますか?
まず簡単に分かる事として,
- $120$ 以下の正整数のうち, $2$ の倍数は $60$ 個.
- $120$ 以下の正整数のうち, $3$ の倍数は $40$ 個.
です.
ここから, $2$ の倍数または $3$ の倍数となる個数は $60+40=100$ 個だ!!と答えたいところですが, そう簡単にも行きません.
なぜなら, $2$ の倍数と $3$ の倍数には重複があるからです.
実際, $2$ の倍数と $3$ の倍数をそれぞれ列挙してみると,
- $1$, $2$, $3$, $4$, $5$, $6$, $7$, $8$, $9$, $10$, $11$, $12$, $\dots$
- $1$, $2$, $3$, $4$, $5$, $6$, $7$, $8$, $9$, $10$, $11$, $12$, $\dots$
となり, $6,12,\dots$ が重複していることが分かります.
$6$ の倍数は $2$, $3$ 両方の倍数であるので, この部分が $2$ 回カウントされてしまうのです.
以上の事から, $60+40=100$ とすると, $6$の倍数分だけ余剰にカウントしてしまう ため, 正しい答えが得られていないという事が分かります.
ここでも先の章と同じく, うまくいかない原因が明確に分かっているのでそれを解消する方向で考えてみましょう.
すると, やりたいことはとても単純で, 足しすぎたのなら余剰分を引けば良いのです.
そして今回はまさに余剰分が $120$ 以下の正整数で $6$ の倍数の個数 $=20$ 個というのが直ちに分かります.
つまり, $40+60$ から, 余剰分 $20$ を引いた $40+60-20=80$ が正しい答えとして得られるのです.
包除原理を説明する上でベン図が良く用いられるので, そちらも紹介します.
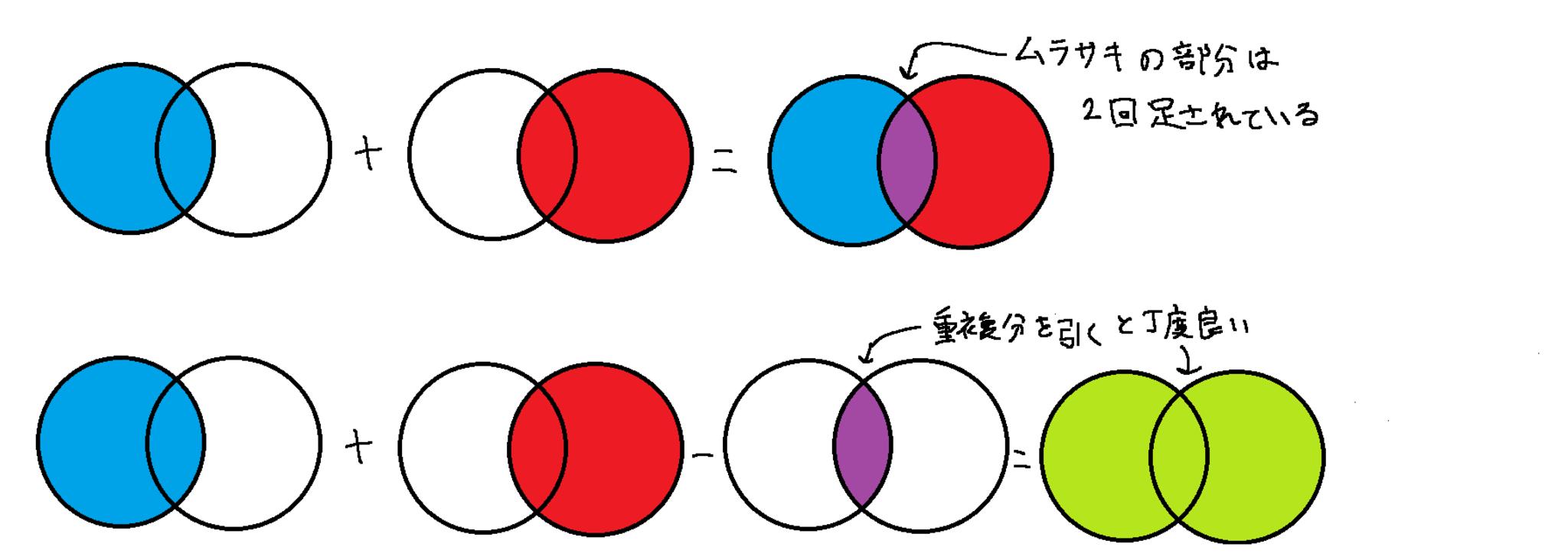包除原理(条件2つ)
これを式で表すと, 以下の通りです.
$A_1,A_2$ を集合とする.
この時, $$|A_1\cup A_2|=|A_1|+|A_2|-|A_1\cap A_2|$$
先ほどの例で言うと, $A_1=\{120\text{以下の2の倍数である正整数}\},\ A_2=\{120\text{以下の3の倍数である正整数}\}$ となります.
それでは次に条件を3つに増やしてみましょう.
$120$ 以下の正整数のうち, $2$ の倍数または $3$ の倍数または $5$ の倍数であるものはいくつありますか?
- $120$ 以下の正整数のうち, $2$ の倍数は $60$ 個.
- $120$ 以下の正整数のうち, $3$ の倍数は $40$ 個.
- $120$ 以下の正整数のうち, $5$ の倍数は $24$ 個.
です.
今回も, 単純に $60+40+24$ を計算するとどれだけ重複して足してしまっているかを考えてみましょう.
先ほど同様, $2$ の倍数かつ $3$ の倍数すなわち, $6$ の倍数は重複して足しています. 他にも, $2$ の倍数かつ $5$ の倍数である $10$ の倍数, $3$ の倍数かつ $5$ の倍数である $15$ の倍数は重複しています.
- $120$ 以下の正整数のうち, $6$ の倍数は $20$ 個.
- $120$ 以下の正整数のうち, $10$ の倍数は $12$ 個.
- $120$ 以下の正整数のうち, $15$ の倍数は $8$ 個.
であるので, $60+40+24$ から $20+12+8$ を引きましょう.
これで重複は取り除けたでしょうか.
表を書いて確認してみましょう.
以下の表は, $2$ の倍数か否か, $3$ の倍数か否か, $5$ の倍数か否かで$8$通りに分類した時, それが各項の加算減算に寄与しているかを表しています.
| 2の倍数 | 3の倍数 | 5の倍数 | 2の倍数に+1 | 3の倍数に+1 | 5の倍数に+1 | 6の倍数に-1 | 10の倍数に-1 | 15の倍数に-1 | 合計 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| o | o | o | 1 | 1 | 1 | -1 | -1 | -1 | 0 | ||
| o | o | x | 1 | 1 | 0 | -1 | 0 | 0 | 1 | ||
| o | x | o | 1 | 0 | 1 | 0 | -1 | 0 | 1 | ||
| o | x | x | 1 | 0 | 0 | 0 | 0 | 0 | 1 | ||
| x | o | o | 0 | 1 | 1 | 0 | 0 | -1 | 1 | ||
| x | o | x | 0 | 1 | 0 | 0 | 0 | 0 | 1 | ||
| x | x | o | 0 | 0 | 1 | 0 | 0 | 0 | 1 | ||
| x | x | x | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
この表をみると, $2$ の倍数かつ$3$ の倍数かつ $5$ の倍数が上手く計上出来ていないようです. (2の倍数でも3の倍数でも5の倍数でもないものも計上されていませんが, それはもともと足されないのが正解のものなので正常な結果です.)
つまり, $(60+40+24)-(20+12+8)$ に
- $120$ 以下の正整数のうち, $30$ の倍数は $4$ 個.
を足せば過不足なく計算ができることが分かります.
よって, 答えは $(60+40+24)-(20+12+8)+4=88$ です.
これもベン図で確認をします.
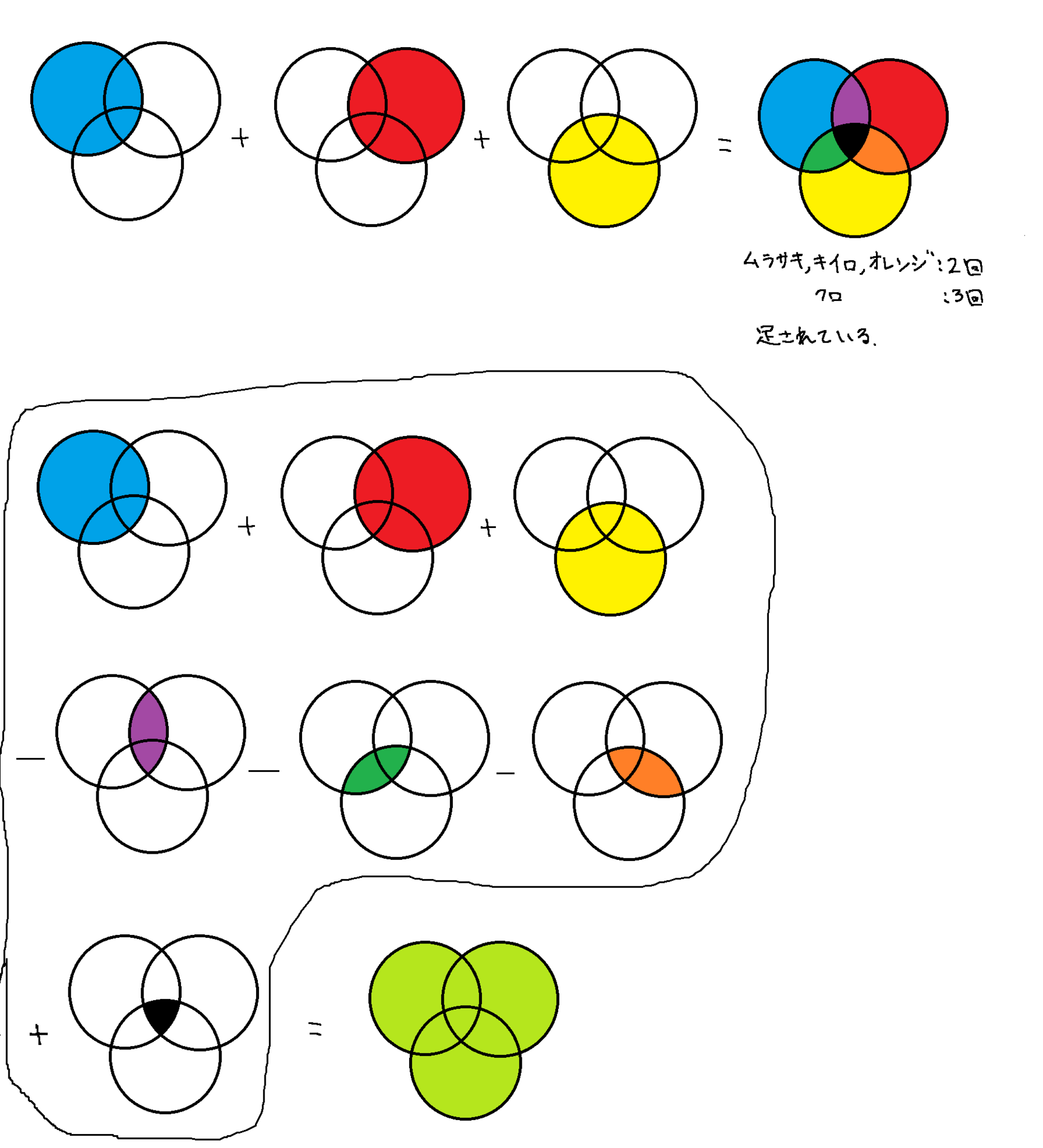包除原理(条件3つ)
線で区切られた各部分が丁度1回ずつ足されているのを確かめてみてください.
$A_1,A_2,A_3$ を集合とする.
この時, $$\begin{aligned}|A_1\cup A_2\cup A_3|=&|A_1|+|A_2|+|A_3|\\
&-|A_1\cap A_2|-|A_1\cap A_3|-|A_2\cap A_3|+|A_1\cap A_2\cap A_3|\end{aligned}$$
条件が2つ,3つ...と来たので次は一般の場合の包除原理を紹介します.
$A_1,A_2,\dots,A_{n}$ を有限集合とする.
$S_n=\{1,2,\dots,n\}$ とする.
$\emptyset\subsetneq T\subset S_n$ に対し,
$\displaystyle\bigcup_{i\in T}A_i$ で, $T$ に含まれるすべての番号 $i$ に対して, $A_i$ の和集合を取った集合を表す.
$\displaystyle\bigcap_{i\in T}A_i$ は共通部分を取った集合を表す.
この時,
$$\left|\bigcup_{i\in S_n}A_i\right|=\sum_{T\subset S_n,T\neq\emptyset}(-1)^{|T|+1}\left|\bigcap_{i\in T}A_{i}\right|$$
が成り立つ.
見た目がとても厳ついですが, やっていることは足してから重複を取り除いて, 取り除きすぎた所を足して, また引いて...を繰り返しているだけです.
$n=2$ の時,
$|A_1\cup A_2|=|A_1|+|A_2|-|A_1\cap A_2|$
$n=3$ の時,
$\begin{aligned}|A_1\cup A_2\cup A_3|=&|A_1|+|A_2|+|A_3|\\
&-|A_1\cap A_2|-|A_1\cap A_3|-|A_2\cap A_3|+|A_1\cap A_2\cap A_3|\end{aligned}$
となり, 確かに上の方で具体例から導いた式と一致している.
帰納法を用いる.
$n=1$ の時, 定理の式は両辺とも $|A_1|$ で一致している.
$n=2$ の時, 定理の式は具体例でみた事を一般の集合にしてちゃんと議論し直すだけなので省略.
$k=n-1$ で,
$$\left|\bigcup_{i\in S_k}A_i\right|=\sum_{T\subset S_k,T\neq\emptyset}(-1)^{|T|+1}\left|\bigcap_{i\in T}A_{i}\right|$$
が成り立つとする.
$\displaystyle \bigcup_{i\in S_k}A_i=B$ とおくと, $\displaystyle \bigcup_{i\in S_n}A_i=B\cup A_n$ である.
また, $B\cap A_n=\bigcup_{i\in S_k}(A_i\cap A_n)$ であるので, $n=2,k$ の場合の包除原理から,
$$\begin{aligned} \left|\bigcup_{i\in S_n}A_i\right|&=|B\cup A_n|\\ &=|B|+|A_n|-|B\cap A_n|\\ &=\sum_{T\subset S_k,T\neq\emptyset}\left((-1)^{|T|+1}\left|\bigcap_{i\in T}A_{i}\right|\right)+|A_n|-\sum_{T\subset S_k,T\neq\emptyset}\left((-1)^{|T|+1}\left|\bigcap_{i\in T}(A_{i}\cap A_n)\right|\right)\\ &=\sum_{T\subset S_k,T\neq\emptyset}\left((-1)^{|T|+1}\left|\bigcap_{i\in T}A_{i}\right|\right)+|A_n|+\sum_{T\subset S_k,T\neq\emptyset}\left((-1)^{|T\cup\{n\}|+1}\left|\bigcap_{i\in T\cup\{n\}}A_{i}\right|\right)\\ &=\sum_{T\subset S_n,T\neq\emptyset}\left((-1)^{|T|+1}\left|\bigcap_{i\in T}A_{i}\right|\right) \end{aligned}$$
よって示された.
かなりごつい式なので補足します.
$2$ 行目から $3$ 行目へは, $n=k$ の場合の包除原理の式をそれぞれ代入しています.
$3$ 行目から $4$ 行目へは, 3項目でシグマを走っていた $T$ を $T\cup\{n\}$ に置き換えています.
ここで $(A_1\cap A_n)\cap(A_2\cap A_n)\cap\dots\cap(A_k\cap A_n)=A_1\cap A_2\cap\dots\cap A_k\cap A_n$ であることを用いています.
$4$ 行目から $5$ 行目へは, シグマを1つに纏めています. 4行目の
- 1項目のシグマは$n$ を含まない全ての $T$ を動いています.
- 2項目は $T=\{n\}$ に対応しています.
- 3項目のシグマは$n$ を含み, $\{n\}$とは異なる全ての $T$ を動いています.
これらを足し合わせると全ての $0\subsetneq T\subset S_n$ が網羅されている事が分かると思います.
さてここまで一般の包除原理を紹介しましたが, 競技数学でこの一般の形の包除原理をやるだけという問題はあまり見ないと思います.
というのも,包除原理右辺のシグマは $0\subsetneq T\subset S_n$ 全体を足し合わせますが, $S_n$ の部分集合は $2^n$ 個あり, とても手計算でできない大きさとなるためです.
実際, $n=5$ で $2^5=32$ であるのでこの時点でかなりの筋力を要するでしょう.
そのため, 手計算で答えを求める類の問題で登場する包除原理は何らかの特殊な形をしていることが多いです.
特殊というのは例えば, "実は大半の部分が消える", "二項係数の計算などに帰着できる" , "集合の大きさに一様性がある" 等様々です.
ここでは, "集合の大きさに一様性がある" 場合にどうなるかを見ていきます.
$\left|\bigcap_{i\in T}A_{i}\right|$ が $|T|$ のみに依存するケースを紹介します.
$\left|\bigcap_{i\in T}A_{i}\right|=f(|T|)$ が任意の $T\subset S_n$ で矛盾なく成り立つような $f$ が存在すれば, 包除原理は以下の通りになります.
$$\left|\bigcup_{i\in S_n}A_i\right|=\sum_{t=1}^{n}\binom{n}{t}(-1)^{t+1}f(t)$$
証明については, $|T|$ の値毎に足し合わせる事で示せます. (これもある種の主客転倒のような考えなので是非証明を完了させてみてください.)
おまけ
包除原理はある種の一般化をすることが出来ます.
$X$ を集合とする.
$f:2^{X}\to \mathbb{R}$ が加法的集合関数であるとは, $A\cap B=\emptyset$ である任意の $A,B\subset X$ に対して, $f(A\cup B)=f(A)+f(B)$ が成り立つことをいう.
ここで, $2^{X}$ は $X$ の冪集合(部分集合を全て集めた集合)である.
一般の文脈では加法的集合関数はもう少し広く扱える定義がされます. 今回のはその特別な場合です.
記号の定義は包除原理の時と同じとする.
$f$ を加法的集合関数とする時,
$$f\left(\bigcup_{i\in S_n}A_i\right)=\sum_{T\subset S_n,T\neq\emptyset}(-1)^{|T|+1}f\left(\bigcap_{i\in T}A_{i}\right)$$
$f(A)=|A|$ で定めると, $f$ は加法的集合関数です. この $f$ に対して加法的集合関数の包除原理を適用すると通常の包除原理が得られます.
証明は大部分が通常の包除原理と同じであるので以下に証明のヒントだけ記載して, 細部は省略します.
証明のヒント
- $A=(A\setminus B)\cup (A\cap B)$
- $B=(B\setminus A)\cup (A\cap B)$
- $A\cup B=(A\setminus B)\cup (B\setminus A)\cup(A\cap B)$
さらに各右辺に表れる集合はそれぞれ互いに素.(共通部分をもたない)
$120$ 以下の正整数で, $2$ の倍数または $3$ の倍数であるような数の総和を求めよ.
解答
$X\subset \{1,2,\dots,120\}$ に対し, $X$ の要素の総和を $f(X)$ とすると, $f$ は加法的集合関数である.
$120$ 以下の正整数で $2,3,6$ の倍数であるものの集合をそれぞれ $A,B,C(=A\cap B)$ とすると, 簡単な計算により, $f(A)=3660,\ f(B)=2460,\ f(C)=1260$ である.
よって, 求める値は $f(A\cup B)=f(A)+f(B)-f(C)=4860$
対象をまとめる, 対象の対称性に注目する
次は知識の典型ではなく, 考え方の典型です.
数え上げでは個々を追うと計算が大変でも, 全体でみると計算がしやすい方法があるというのは主客転倒章でも触れたことです. この章ではそこに再び焦点をあてます.
まずは以下の問題を考えてみましょう.
$99999$ 以下の非負整数のうち, $10$ 進法表記で各位の数の和が $15$ の倍数である数の総和を求めてください.
$99999$ 以下の非負整数の各位の数の和は $0$ 以上 $45$ 以下です.
よって, 各位の数の和が $0,15,30,45$ であるような数の総和が求まれば良いです.
$0,45$ に関してはそれぞれ$1$通りなので簡単です.
各位の数の和が $15,30$ となる数の和はどうでしょうか.
$\vdots\\\vdots$
素直に計算しようとすると大変そうですね. そこで, 対象を纏めるという事をします.
具体的には, $9+9+9+9+9=45=15+30$ を利用します.
すなわち, 非負整数 $n$ の十進法表記 $n=a*10^4+b*10^3+c*10^2+d*10+e$ が $a+b+c+d+e=15$ を満たすとき, $99999-n=(9-a)*10^4+(9-b)*10^3+(9-c)*10^2+(9-d)*10+(9-e)$ であり, $(9-a)+(9-b)+(9-c)+(9-d)+(9-e)=30$ となります.
逆に各位の数の和が $30$ である非負整数 $n$ については, $99999-n$ は各位の数の和が $15$ となります.
よって, 各位の数の和がそれぞれ $15,30$ である数の集合は, $n+m=99999$ となるように1対1のペアが作れます.
従って, 各位の数の和が $15,30$ となる全ての数の総和は, $99999*\text{(各位の数の和が15となる非負整数の数)}$ となります.
各位の数の和が $15$ となる非負整数の個数は, $15$以下の$5$つの非負整数で和が $15$ になる組み合わせ数から $15$以下の$5$つの非負整数で和が $15$ になり, 少なくとも一つが $10$ 以上となる組み合わせ数を引くことで, $\binom{19}{4}-5*\binom{9}{4}=3246$ 通りです.
よって各位の数の和が$0,45$ の場合と合わせて, 求める答えは $0+99999+99999*3246=324696753$ となります.
$9699690(=\text{20以下の素数の総乗}=2*3*5*7*11*13*17*19)$ 未満の非負整数のうち, $20$ 以下の素因数をもつ数の総和を求めてください.
この問題は包除原理の章の最後に紹介した問題の制約が大きいverです.
つまり, 包除原理を用いることで解くことができますが, それは恐らくかなりの計算が必要となってしまいます.
そこで, 対称性を利用した解き方を紹介します.
$20$ 以下の素数で割り切れる非負整数を良い数と呼ぶことにします.
この時, $n$ が良い数$\Leftrightarrow 9699690-n$ が良い数 という, 先ほどの問題と似た性質が現れます.
つまり, $9699690$ 未満の良い数のうち $0$ でない数の平均値は $\dfrac{9699690}{2}$ となります.
総和=平均値*要素数ですので, 後は $9699690$ 未満の良い数の個数が求まればよいです.
$9699690$ 未満の良い数でない数を数えると, $9699690*\frac{1}{2}*\frac{2}{3}*\frac{4}{5}*\frac{6}{7}*\frac{10}{11}*\frac{12}{13}*\frac{16}{17}*\frac{18}{19}=2^{12}*3^{4}*5^{1}=1658880$ 個あることが分かります(なぜこの計算で求まるかは演習とします).
よって$9699690$ 未満の良い数は $9699690-1658880=8040810$ 個あるので, 求める答えは
$$(8040810-1)*\dfrac{9699690}{2}=38996677324605$$
となります.
ここまでは数え上げる対象がバラバラで, それを纏める事で数えやすくするという事を考えてきました.
この章の最後にその逆である数えるべき対象がまとまっているので, バラバラの状態に一旦落とし込むタイプの問題を紹介します.
かなりお気に入りの一問です.
$9$ つの箱 $1,2,\dots,9$ があり，これらに $9$ 種類の玉 $1,2,\dots,9$ を次をみたすように入れることを考えます．
- 各 $i=1,2,\dots,9$ に対し箱 $i$ には 玉 $i$ と玉 $i+1$ が合わせて $10$ 個入っており，それ以外の種類の玉は1つも入っていない．
ただし玉 $10$ は玉 $1$ を表すものとし，また $1$ 種類の玉しか入っていない箱があっても構いません． 箱に入っている玉 $i$ の総数を $a_i$ とするとき，組 $(a_1,a_2,\dots,a_9)$ としてあり得るものは何通りありますか？
問題へのリンク
ヒント
いくつかの "各箱の各玉の数"の組から同じ "各玉の数の和"の組が現れます.
よって, 前者を考えるのは遠回りのようですが, 扱い易いのは圧倒的に前者です.
まずは前者について考えて, どのような条件の前者の組が, 同一の後者の組となるかを考えてみましょう.
二項係数
数え上げの問題では二項係数が度々登場します.
この章では二項係数に因む等式をその導出の道具ごとにいくつか紹介します.
なお実際には素朴な定義等から示した方が早く, 楽な等式もありますが, ここでは分類上難しい方法で示している場合があります. 余力のある方は楽な方法も考えてみてください.
この章では二項係数を $\binom{n}{k}\left(={}_{n}\mathrm{C}_{k}\right)$ で表し, $n< k$ に対して $\binom{n}{k}=0$ とする.
また, 特筆されていない場合全て $n>0$ とする. ($n=0$で成り立たない等式もいくつかあります.)
多項式と絡めるタイプ
多項式, とりわけ二項定理から二項係数の面白い性質が色々と現れます.
$$ (x+y)^n=\sum_{k=0}^{n}x^ky^{n-k}\binom{n}{k}$$
例えば, $x=y=1$ や, $x=-1,\ y=1$ を代入してみると,
$$2^n=\sum_{k=0}^{n}\binom{n}{k},\quad 0=\sum_{k=0}^{n}(-1)^{k}\binom{n}{k}$$
を得ます.
さらに, 定理1は多項式であるので, 微積分ができます.
定理1の両辺を$x$で微分してみましょう.
$$n(x+y)^{n-1}=\sum_{k=1}^{n}kx^{k-1}y^{n-k}\binom{n}{k}$$
ここに再び $x=y=1$ や, $x=-1,\ y=1$ を代入してみると,
$$n2^{n-1}=\sum_{k=0}^{n}k\binom{n}{k},\quad 0=\sum_{k=0}^{n}(-1)^{k-1}k\binom{n}{k}$$
となります.
今度は等式1の両辺を$x$ について $0$ から $x$ まで積分してみると,
$$\frac{(x+y)^{n+1}-y^{n+1}}{n+1}=\sum_{k=0}^{n}\frac{1}{k+1}x^{k+1}y^{n-k}\binom{n}{k}$$
ここに三度 $x=y=1$ や, $x=-1,\ y=1$ を代入してみると,
$$\frac{2^{n+1}-1}{n+1}=\sum_{k=0}^{n}\frac{1}{k+1}\binom{n}{k},\quad \frac{-1}{n+1}=\sum_{k=0}^{n}\frac{(-1)^{k+1}}{k+1}\binom{n}{k}$$
となります.
各式をさらに積分したり, $x$ をかけてから微分したり, $(x,y)$ に他の値を代入した等々, 様々なバリエーションで他の等式を作り出すことができます.
皆さんもガチャガチャ式をいじってみて好きな等式が出来たら是非tweetでもしてください.
組み合わせの本筋から外れますが, 二項係数で問題を作ろうとしてちょっと面白い等式が作れたので観賞用問題として紹介します. (初手発想ゲーです.)
$x$ を $\tan{x}$ が定義される実数とします.
$$\frac{\cos{nx}}{\cos^{n}{x}}=\sum_{k=0}^{\left\lfloor\frac{n}{2}\right\rfloor}(-1)^k\tan^{2k}{x}\binom{n}{2k}$$
を示してください.
解答の概略
$(\cos{x}+i\sin{x})^n$ に二項定理を用いる.
$$\sum_{k=0}^{15}\dfrac{(-1)^k}{(k+1)(k+3)}\binom{n}{k}=\frac{a}{b}$$
を満たす互いに素な正整数 $a,b$ について $a+b$ を求めてください.
解答
$(x+1)^n$ を $0$ から $x$ まで積分, $x$ を掛ける, $0$ から $x$ まで積分をすると,
$$\frac{1}{n+1}\left(\frac{(x+1)^{n+3}-1}{n+3}-\frac{(x+1)^{n+2}-1}{n+2}-\frac{x^2}{2}\right)=\sum_{k=0}^{k}\frac{x^{k+3}}{(k+1)(k+3)}\binom{n}{k}$$
となる. ($x(x+1)^m=(x+1)^{m+1}-(x+1)^m$ を使うと幾分か計算が楽である.)
特に, $x=-1$ を代入して,
$$\begin{aligned}\sum_{k=0}^{15}\dfrac{(-1)^{k}}{(k+1)(k+3)}\binom{n}{k}&=\frac{(n+2)(n+3)-2}{2(n+1)(n+2)(n+3)}\\ &=\frac{n+4}{2(n+2)(n+3)} \end{aligned}$$
である.
$n=15$ で,
$$\frac{19}{612}=\frac{a}{b}$$
である. よって求める答えは $19+612=631$
問題を複数通りで解釈するタイプ
二項係数がらみの問題を2通りの解釈で解くことによって二項係数間の等式を示すことができることがあります.
ここでは汎用性の高そうな2つの等式を紹介します.
正整数 $m,p$ の値と, 長さ $p$ の正整数列 $n_1,n_2,\dots,n_p$ は与えられたものとする.
$$\sum_{\sum_{i=1}^{p}k_i=m}\prod_{i=1}^{p}\binom{n_i}{k_i}=\binom{\sum_{i=1}^{p}n_i}{m}$$
例えば $p=2$ の時 $$\sum_{k_1+k_2=m}\binom{n_1}{k_1}\binom{n_2}{k_2}=\binom{n_1+n_2}{m}$$ となり, 特に $n_1=n_2=m=N$ の時,
$$\sum_{k=0}^{N}\binom{N}{k}^2=\binom{2N}{N}$$
という有名等式が得られます.
ヴァンデルモンドの畳み込みをある問題の答えを2通りに表すことによって示します.
AMC高校には $p$ 個のクラスがあり, $i$ 個目のクラスには $n_i$ 人の生徒が在籍しています.
計 $n_1+n_2+\dots+n_p$ 人の中から計 $m$ 人を選出する方法は何通りありますか.
この問題を解く $1$ つ目の方法はクラスを完全に無視することです.
クラス分けを無視すると, この問題は単に $\sum_{i=1}^{p}n_i$ 人の中から $m$ 人を選ぶ問題なので, $\binom{\sum_{i=1}^{p}n_i}{m}$ 通りが答えであると分かります.
次にクラスごとに考えてみましょう.
$i$ 番目のクラスから $k_i$ 人を選ぶとして,この値を一旦固定すると, 各クラスでの人の選び方は $\binom{n_i}{k_i}$ 通りです. この選び方はクラスごとに独立であるため, 各クラスから $(k_1,k_2,\dots,k_p)$ 人選ぶ方法は $\prod_{i=1}^{p}\binom{n_i}{k_i}$ 通りです.
これを $\sum_{i=1}^{p}k_i=m$ を満たす$k_i$の組について足し合わせればよいので, この問題の答えは $$\sum_{\sum_{i=1}^{p}k_i=m}\prod_{i=1}^{p}\binom{n_i}{k_i}$$ であると分かります.
ここで2通りの表示で得た値は同じ問題の答え(すなわち同じ値)であるので, ヴァンデルモンドの畳み込みが示されました.
続いての等式を紹介します.
$$\sum_{i=k}^{n}\binom{i}{k}=\binom{n+1}{k+1},\quad(n\ge k)$$
この恒等式を経路問題を $2$ 通りの表示で答えることによって示してみましょう.
$xy$ 平面上の点 $(0,0)$ に点 $P$ があります. この点は $(x,y)$ にいる時に $(x+1,y)$ または $(x,y+1)$ に移動することを繰り返します.
$(0,0)$ から $(n-k,k+1)\ (n\ge k)$ へ移動する方法は何通りありますか.
まず$1$ つ目の解法としては素直に経路問題として解く方法で, $\binom{n-k+k+1}{k+1}=\binom{n+1}{k+1}$ がこの問題の答えであると分かります.
次に, ひねくれた解き方をします.
$(n-k,k+1)$ へ移動するとき, $(i,k)$ から $(i,k+1)$ へ移動するような $i$ が各移動経路に対して一意的に存在します.
よって, この $i$ 毎に和を取ることができます.
$(0,0)$ から $(i,k)$ への移動は $\binom{i+k}{k}$ 通り, $(i,k+1)$ から $(n-k,k+1)$ への移動は $1$ 通りであるので, 求める総経路数は
$$\sum_{i=0}^{n-k}\left(\binom{i+k}{k}\times1\right)=\sum_{i=k}^{n}\binom{i}{k}$$
となります.
ここで2通りの表示で得た答えは同じ値であるので, ホッケースティック恒等式が示されました.
$N,M>m$ に対し,
$$\sum_{i=0}^{N}\binom{i+m}{m}\binom{N+M-m-i-1}{M-m-1}=\binom{N+M}{N}$$
を示してください.
解答の概略
$(0,0)$ から $(N,M)$ への移動経路を, $(i,m)$ から $(i,m+1)$ へ移動するような $i$ の値毎に足し合わせる.
二項係数mod $p$
この章の後半では組み合わせ論チックでは無いですが短答式のOMCで役に立つかもしれない二項係数の定理を紹介します.
$p$ を素数, $n>k$ を正整数とする.
この時, $\binom{n}{k}$ が $p$ で割り切れる回数は, $(n-k)+k$ を $p$ 進法表記で(筆算のように)計算する時の繰り上がりの回数と等しい.
$\binom{10}{5}=252$ は $3$ で $2$ 回割り切れる.
$5+5$ を $3$ 進法表記で計算すると,
$
\begin{array}{cc}
&\ \ \ 1\ \ 2 \\
+&\ \ \ 1\ \ 2 \\
&------ \\
&1\ \ 0\ \ 1
\end{array}
$
となり, $1$ の位から $3$ の位へと $3$ の位から $9$ の位への $2$ 回繰り上がりが起こる.
$n,k,n-k$ の $p$ 進法による表示をそれぞれ,
$$n=\sum_{i=0}^{m}a_ip^i,\ k=\sum_{i=0}^{m}b_ip^i,\ n-k=\sum_{i=0}^{m}c_ip^i$$
とする.
この時, $(n-k)+k=n$ の計算時に $p^j$ から $p^{j+1}$ の位へ繰り上がりが
- 起こるとき, $\sum_{i=j+1}^{m}a_ip^i-\sum_{i=j+1}^{m}b_ip^i-\sum_{i=j+1}^{m}c_ip^i= p^{j+1}$
- 起こらないとき, $\sum_{i=j+1}^{m}a_ip^i-\sum_{i=j+1}^{m}b_ip^i-\sum_{i=j+1}^{m}c_ip^i= 0$
に注意する.
$\mathrm{Legendre's}$ の定理より, $\binom{n}{k}$ が $p$ で割り切れる回数 $v$ は,
$\begin{aligned}
v=\sum_{j=1}^{m}\left(\left\lfloor\frac{n}{p^j}\right\rfloor-\left\lfloor\frac{k}{p^j}\right\rfloor-\left\lfloor\frac{n-k}{p^j}\right\rfloor\right)
\end{aligned}$
である.
各 $j$ 毎に, $\left\lfloor\frac{n}{p^j}\right\rfloor-\left\lfloor\frac{k}{p^j}\right\rfloor-\left\lfloor\frac{n-k}{p^j}\right\rfloor$ の値を考える.
$\begin{aligned}
&\left\lfloor\frac{n}{p^j}\right\rfloor-\left\lfloor\frac{k}{p^j}\right\rfloor-\left\lfloor\frac{n-k}{p^j}\right\rfloor\\
&=\sum_{i=j}^{m}a_ip^{i-j}-\sum_{i=j}^{m}b_ip^{i-j}-\sum_{i=j}^{m}c_ip^{i-j}\\
&=\begin{cases}1&(p^{j-1} \text{の位から}p^{j} \text{の位へ繰り上がる})\\0&(p^{j-1} \text{の位から}p^{j} \text{の位へ繰り上がらない})\end{cases}
\end{aligned}$
である.
よって, これを $j=1,2\dots,m$ と足し合わせれば, 定理の主張を得る.
(下から数行目が表示上切れていますが, 上段は繰り上がる, 下段は繰り上がらないです.)
$p$ を素数, $n>k$ を正整数とする.
$n,k$ の $p$ 進法による表示をそれぞれ,
$$n=\sum_{i=0}^{m}a_ip^i,\ k=\sum_{i=0}^{m}b_ip^i,$$
とする.
この時,
$$\binom{n}{k}\equiv\prod_{i=0}^{m}\binom{a_i}{b_i}\mod{p}$$
が成り立つ.
$11=1+2*5, 6=1+1*5$ であり,
$\binom{11}{6}=462\equiv 2=\binom{2}{1}*\binom{1}{1}\mod{5}$ である.
$X=xp+q,\ Y=yp+r$ に対して, $\binom{X}{Y}\equiv \binom{x}{y}\binom{q}{r}\mod{p}$ が示されればこの合同式を $n,k$ について下位の位から順に適用すれば定理の主張が得られる.
- $q< r$ の時
$\begin{aligned}\binom{xp+q}{yp+r}=xp*\binom{xp-1}{yp+r-q-1}*\frac{1}{yp+r-q}*\frac{xp+1}{yp+r-q+1}*\dots*\frac{xp+q}{yp+r}\end{aligned}$
は$p$ の倍数である.
$q< r$ より $\binom{X}{Y}\binom{q}{r}=0$ であるので, 合同式は成立する. - $q\ge r$ の時.
$\begin{aligned}\binom{xp+q}{yp+r}&=\binom{xp+q-r}{yp}*\frac{xp+q}{yp+r}*\frac{xp+q-1}{yp+r-1}*\dots*\frac{xp+q-r+1}{yp+1}\\ &\equiv \binom{xp+q-r}{yp}*\frac{q}{r}*\frac{q-1}{r-1}*\dots*\frac{q-r+1}{1}\\ &=\binom{xp+q-r}{yp}\binom{q}{r}\mod{p} \end{aligned}$
であるので, $r=0$ の場合に合同式 $\binom{xp+q}{yp}\equiv\binom{x}{y}$ が示されればよいが, これは,
$\begin{aligned}\binom{xp+q}{yp}&\equiv\frac{(xp)*((x-1)p)*\dots*((x-y+1)p)}{yp*(y-1)p*\dots*p}*\frac{((p-1)!)^y}{((p-1)!)^y}\\ &\equiv \binom{x}{y}\mod{p}\\ \end{aligned}$
から従う.
$0\le k\le n<3^{10007}$ を満たす整数 $(n,k)$ の組全てについて, $\binom{n}{k}$ を $3$ で割った余りを足し合わせた値を $M$ とします.
$M$ を $10007$ で割った余りを求めてください. 但し, $10007$ は素数です.
解答
$p=10007$ とする.
Lucasの定理より, $2$つの, $3$未満の非負整数からなる長さ$p$ の数列 $(n_0,n_1,\dots,n_{p-1}),\ (k_0,k_1,\dots,k_{p-1})$ の組全てに対して $$\prod_{i=0}^{p-1}\binom{n_i}{k_i}$$ を足し合わせた値を求めればよい.
$3$ 未満の非負整数の組 $n_0,k_0$ の組で $\binom{n_0}{k_0}=1,2$ となる組の数はそれぞれ $5,1$ 通りである.
よって, $a_i,\ b_i$ をそれぞれ $(n_0,n_1,\dots,n_{i}),\ (k_0,k_1,\dots,k_{i})$ の組で, $\prod_{j=0}^{i}\binom{n_j}{k_j}$ の値が $1,2$ となるものの数と定めると,
$a_0=5,\ b_0=1,\ a_{i+1}=5a_{i}+b_{i},\ b_{i+1}=a_{i}+5_{i+1}$ という漸化式がたつ.
これを解くと, $2a_i=6^{i+1}+4^{i+1},\ 2b_i=6^{i+1}-4^{i+1}$ を得る.
よって, $M=3*6^{p-1}+2*4^{p-1}+2(3*6^{p-1}-2*4^{p-1})=9*6^{p-1}-2*4^{p-1}$
である.
Felmatの小定理より, 求める答えは $9*1-2*1\equiv 7$
なお, $a_i,\ b_i$ はFPSを用いると, は $(5+x)^{i+1}$ のそれぞれ偶数次, 奇数次の係数の和であるので, $x=1,-1$ を代入して和や積を取ることで漸化式を陽に解かずに解を求められる.
多項係数
ここで紹介した公式や定理の中には多項係数 $$\frac{\left(\sum_{i=1}^{k}n_k\right)!}{\prod_{i=1}^{k}n_k!}$$
に関する公式や定理に一般化が出来るものがあります.
是非考えてみてください.
おわりに
ここまでお読みいただきありがとうございます.
まだまだ書きたいことはたくさんありましたが, 書き切れなかったのでそれはまたの機会に回そうと思います. (FPSについても書きたかった......)
皆さんも年末年始に是非組み合わせ問題をしましょう!!
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
