4つの円に囲まれたラグビーボールのような図形の面積
問題(数Ⅲ、数Cの範囲で解けます。)
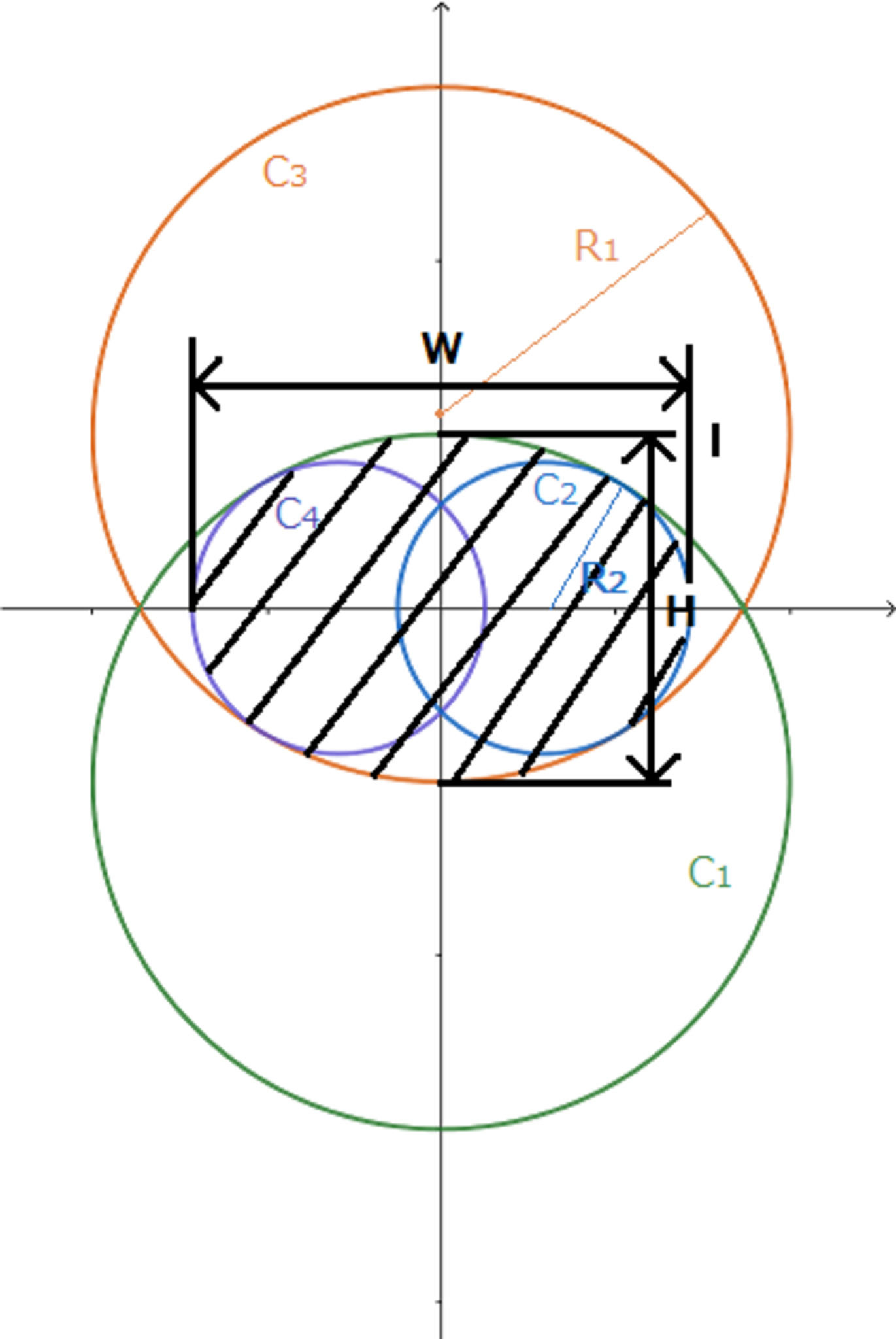円に囲まれた図形
半径$R_1$で中心が$y$軸上にあり、点$(0, \frac{H}{2})$を通る円を円$C_1$、円$C_1$とは$x$軸に対して線対称な円を円$C_3$
半径$R_2$で中心が$x$軸上にあり、点$(\frac{W}{2}, 0)$を通る円を円$C_2$、円$C_2$とは$y$軸に対して線対称な円を円$C_4$とする。
円$C_2、C_4$は、円$C_1$と1点で交わり、円$C_3$とも1点で交わる。
このとき、次の問いに答えよ。
ただし、$0 < 2R_2 < H < W < 2R_1$とする。
１．円$C_1, C_2$を式で表せ。
２．円$C_1, C_2$の交点の一つを点$(x_0, y_0) (x_0, y_0 > 0)$とするとき、$x_0, y_0$をそれぞれ$R_1, R_2, H, W$で表せ。
３．円$C_1, C_2$の中心をそれぞれ点$C_1, C_2$とし、$∠OC_1C_2=θ_0 (0 ≤ θ_0 ≤ \frac{π}{2})$とするとき、円$C_1, C_2, C_3, C_4$で囲まれた図形（図1斜線部）の面積$S$を$θ_0, R_1, R_2, H, W$で表せ。
４．$R_2$を$R_1, H, W$で表せ。
５．次の問いに答えよ。
(a)$\lim_{R_1 \to \infty} R_2$を求めよ。
(b)$\sin θ_0, \tan θ_0, \lim_{R_1 \to \infty} θ_0$をそれぞれ$R_1, R_2, H, W$で表せ。
(c)$\sin θ_0 < θ_0 < \tan θ_0$を利用して$ \lim_{R_1 \to \infty} S$を$H,W$で表せ。
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
模範解答
１．円$C_1, C_2$を式で表せ。
解
円$C_1$
中心を$(0,-y_1) (y_1>0)$とすると
$C_1:x^2+(y+y_1)^2=R_1^2$
$(0,\frac{H}{2})$を通るので
$0^2+(\frac{H}{2}+y_1)^2=R_1^2$
$(\frac{H}{2}+y_1+R_1)(\frac{H}{2}+y_1-R_1)=0$
$y_1=R_1-\frac{H}{2} (∵\frac{H}{2}+y_1+R_1>0)$
$C_1:x^2+(y+R_1-\frac{H}{2})^2=R_1^2$
円$C_2$
中心が$x$軸上、半径$R_2$。
点$(\frac{W}{2},0)$を通るので、中心$(\frac{W}{2}-R_2,0)$。
$C_2:\lbrace x-(\frac{W}{2}-R_2) \rbrace^2+y^2=R_2^2$
$C_2:(x-\frac{W}{2}+R_2)^2+y^2=R_2^2$
$ $
２．円$C_1, C_2$の交点の1つを点$(x_0, y_0) (x_0, y_0 > 0)$とするとき、$x_0, y_0$をそれぞれ$R_1, R_2, H, W$で表せ。
解
![点!FORMULA[71][-1346103092][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20221225171157.png?alt=media)
点$(x_0, y_0)$
円$C_1, C_2$は1点で交わるので、半径が同一線上にある。（図2）
原点$O$, 点$(0, -R+\frac{H}{2})$, 点$(\frac{W}{2}-R_2, 0)$を頂点とする直角三角形と
点$(x_0, 0)$, 点$(x_0, y_0)$, 点$(\frac{W}{2}-R_2, 0)$を頂点とする直角三角形は相似なので
$R_2:(R_1-R_2)=\lbrace x_0-(\frac{W}{2}-R_2) \rbrace:(\frac{W}{2}-R_2)=y_0:(R_1-\frac{H}{2})$
$R_2:(R_1-R_2)=\lbrace x_0-(\frac{W}{2}-R_2) \rbrace:(\frac{W}{2}-R_2)$
$(R_1-R_2)x_0-(R_1-R_2)(\frac{W}{2}-R_2)=R_2(\frac{W}{2}-R_2)$
$(R_1-R_2)x_0=R_1(\frac{W}{2}-R_2)$
$x_0=\frac{R_1}{R_1-R_2}(\frac{W}{2}-R_2) (R_1-R_2>0)$
$R_2:(R_1-R_2)=y_0:(R_1-\frac{H}{2})$
$y_0=\frac{R_2}{R_1-R_2}(R_1-\frac{H}{2})$
$ $
３．円$C_1, C_2$の中心をそれぞれ点$C_1, C_2$とし、$∠OC_1C_2=θ_0 (0 ≤ θ_0 ≤ \frac{π}{2})$とするとき、円$C_1, C_2, C_3, C_4$で囲まれた図形（図1斜線部）の面積$S$を$θ_0, R_1, R_2, H, W$で表せ。
解
（図2）より
$\frac{S}{4}=(中心C_1半径R_1の扇形)-(△OC_1C_2)+(中心C_2半径R_2の扇形)$
$=\frac{θ_0}{2}R_1^2-\frac{1}{2}(R_1-\frac{H}{2})(\frac{W}{2}-R_2)+\frac{1}{2}(\frac{π}{2}-θ_0)R_2^2$
$=\frac{θ_0}{2}R_1^2-\frac{1}{2}R_1(\frac{W}{2}-R_2)+\frac{H}{4}(\frac{W}{2}-R_2)+(\frac{π}{4}-\frac{θ_0}{2})R_2^2$
$S=2θ_0R_1^2-2R_1(\frac{W}{2}-R_2)+H(\frac{W}{2}-R_2)+(π-2θ_0)R_2^2$
$ $
４．$R_2$を$R_1, H, W$で表せ。
$C_1:x^2+(y+R_1-\frac{H}{2})^2=R_1^2$は$(x_0,y_0)$を通るので
$x_0^2+(y_0+R_1-\frac{H}{2})^2=R_1^2$
$x_0^2+y_0^2+2y_0 (R_1-\frac{H}{2})+(R_1-\frac{H}{2})^2=R_1^2$
$\frac{R_1^2}{(R_1-R_2)^2}(\frac{W}{2}-R_2)^2 +\frac{R_2^2}{(R_1-R_2)^2}(R_1-\frac{H}{2})^2 +\frac{2R_2}{R_1-R_2}(R_1-\frac{H}{2})^2+(R_1-\frac{H}{2})^2=R_1^2$
$\frac{R_1^2}{(R_1-R_2)^2}(\frac{W}{2}-R_2)^2 +\frac{R_2^2}{(R_1-R_2)^2}(R_1-\frac{H}{2})^2 +\frac{R_1+R_2}{R_1-R_2}(R_1-\frac{H}{2})^2 -R_1^2=0$
$\frac{R_1^2}{(R_1-R_2)^2}(\frac{W}{2}-R_2)^2 +\frac{R_2^2+R_1^2-R_2^2}{(R_1-R_2)^2}(R_1-\frac{H}{2})^2 -R_1^2=0$
$\frac{R_1^2}{(R_1-R_2)^2}(\frac{W}{2}-R_2)^2 +\frac{R_1^2}{(R_1-R_2)^2}(R_1-\frac{H}{2})^2-R_1^2=0$
$(\frac{W}{2}-R_2)^2+(R_1-\frac{H}{2})^2-(R_1-R_2)^2=0 (\frac{R_1^2}{(R_1-R_2)^2} > 0)$
$(\frac{W}{2}-R_2)^2+ \lbrace (R_1-\frac{H}{2})+(R_1-R_2) \rbrace \lbrace (R_1-\frac{H}{2})-(R_1-R_2) \rbrace =0$
$(\frac{W}{2}-R_2)^2+(2R_1-R_2-\frac{H}{2})(R_2-\frac{H}{2})=0$
$(\frac{W}{2})^2-WR_2+R_2^2+2R_1(R_2-\frac{H}{2})-R_2^2+(\frac{H}{2})^2=0$
$(\frac{W}{2})^2-WR_2+2R_1 R_2-HR_1+(\frac{H}{2})^2=0$
$(2R_1-W)R_2=HR_1-(\frac{H}{2})^2-(\frac{W}{2})^2$
$R_2=\frac{HR_1-(\frac{H}{2})^2-(\frac{W}{2})^2}{2R_1-W} (2R_1-W > 0)$
$=\frac{4HR_1-H^2-W^2}{8R_1-4W}$
$ $
５．次の問いに答えよ。
(a)$\lim_{R_1 \to \infty} R_2$を求めよ。
解
$\lim_{R_1 \to \infty} R_2 = \lim_{R_1 \to \infty} \frac{4HR_1-H^2-W^2}{8R_1-4W}$
$=\lim_{R_1 \to \infty}\frac{4H-\frac{H^2}{R_1}-\frac{W^2}{R_1}}{8-\frac{4W}{R_1}}$
$=\frac{4H}{8}$
$=\frac{H}{2}$
$ $
(b)$\sin θ_0, \tan θ_0, \lim_{R_1 \to \infty} θ_0$をそれぞれ$R_1, R_2, H, W$で表せ。
解
（図2）から
$\sin θ_0 = \frac{1}{R_1-R_2}(\frac{W}{2}-R_2)$
$\tan θ_0=\frac{\frac{W}{2}-R_2}{R_1-\frac{H}{2}}=\frac{1}{R_1-\frac{H}{2}}(\frac{W}{2}-R_2)$
$\lim_{R_1 \to \infty} \sin θ_0$
$= \lim_{R_1 \to \infty} \frac{1}{R_1-R_2}(\frac{W}{2}-R_2) = 0$
$\lim_{R_1 \to \infty} θ_0 = 0 (0 ≤ θ_0 ≤ \frac{π}{2})$
$ $
(c)$\sin θ_0 < θ_0 < \tan θ_0$を利用して$ \lim_{R_1 \to \infty} S$を$H,W$で表せ。
$S=2θ_0R_1^2-2R_1(\frac{W}{2}-R_2)+(π-2θ_0)R_2^2+H(\frac{W}{2}-R_2)$
$2\sin θ_0 R_1^2-2R_1(\frac{W}{2}-R_2)$
$< 2θ_0 R_1^2-2R_1(\frac{W}{2}-R_2)$
$< 2\tan θ_0 R_1^2-2R_1(\frac{W}{2}-R_2)$
$\lim_{R_1 \to \infty} \lbrace 2\sin θ_0 R_1^2-2R_1(\frac{W}{2}-R_2) \rbrace$
$=\lim_{R_1 \to \infty} \lbrace 2\frac{1}{R_1-R_2}(\frac{W}{2}-R_2) R_1^2-2R_1(\frac{W}{2}-R_2) \rbrace$
$=\lim_{R_1 \to \infty} 2R_1(\frac{W}{2}-R_2)(\frac{R_1}{R_1-R_2}-1)$
$=\lim_{R_1 \to \infty} 2R_1(\frac{W}{2}-R_2)\frac{R_2}{R_1-R_2}$
$=\lim_{R_1 \to \infty} 2(\frac{W}{2}-R_2)\frac{R_1R_2}{R_1-R_2}$
$=\lim_{R_1 \to \infty} 2(\frac{W}{2}-R_2)\frac{R_2}{1-\frac{R_2}{R_1}}$
$=2(\frac{W}{2}-\frac{H}{2})\frac{H}{2}$
$=H(\frac{W}{2}-\frac{H}{2})$
$\lim_{R_1 \to \infty} \lbrace 2\tan θ_0 R_1^2-2R_1(\frac{W}{2}-R_2) \rbrace$
$=\lim_{R_1 \to \infty} \lbrace 2\frac{1}{R_1-\frac{H}{2}}(\frac{W}{2}-R_2)R_1^2-2R_1(\frac{W}{2}-R_2) \rbrace$
$=\lim_{R_1 \to \infty} 2R_1(\frac{W}{2}-R_2)(\frac{R_1}{R_1-\frac{H}{2}}-1)$
$=\lim_{R_1 \to \infty} 2R_1(\frac{W}{2}-R_2)\frac{\frac{H}{2}}{R_1-\frac{H}{2}}$
$=\lim_{R_1 \to \infty} 2(\frac{W}{2}-R_2)\frac{\frac{H}{2}R_1}{R_1-\frac{H}{2}}$
$=\lim_{R_1 \to \infty} 2(\frac{W}{2}-R_2)\frac{\frac{H}{2}}{1-\frac{H}{2R_1}}$
$=2(\frac{W}{2}-\frac{H}{2})\frac{H}{2}$
$=H(\frac{W}{2}-\frac{H}{2})$
はさみうちの原理より
$\lim_{R_1 \to \infty} \lbrace 2θ_0 R_1^2-2R_1(\frac{W}{2}-R_2) \rbrace=H(\frac{W}{2}-\frac{H}{2})$
$\lim_{R_1 \to \infty} S$
$=\lim_{R_1 \to \infty} \lbrace 2θ_0R_1^2-2R_1(\frac{W}{2}-R_2)+(π-2θ_0)R_2^2+H(\frac{W}{2}-R_2) \rbrace$
$=H(\frac{W}{2}-\frac{H}{2})+π(\frac{H}{2})^2+H(\frac{W}{2}-\frac{H}{2})$
$=\frac{π}{4}H^2+2H(\frac{W}{2}-\frac{H}{2})$
$=\frac{π}{4}H^2+HW-H^2$