自作問題(1)

今年の大晦日は何曜日か．

$\sqrt{2}$は無理数か．ただし，$\sqrt{2}=1.41$とする．

$2023$を互いに素な$2$つの正整数の和で表す(足す順番は考慮しない)方法は何通りか．

${}^4x = x^{x^{x^x}}$を微分せよ．

${}^nx(n\in\mathbb{Z_{++}})$を微分せよ．

$2023$以下の素数の個数は$300$個以上であることを示せ．

自然数の自然数乗は自然数か．

$0|0$か．

直径の長さが$a$の球を球欠の高さが$\dfrac{a}{3}$となるように切断した立体の体積を求めよ．

問題9で求めた球欠の重心位置を説明せよ．

問題9で求めた球欠の球冠部分の重心位置を説明せよ．

$\phi(n)$が素数となる正整数をすべて求めよ．

$\phi(n)$が半素数となる$100$以下の正整数をすべて求めよ．

$13^4$を$2^4$で割ったあまりを求めよ．

$13^5x-2^5y=1$の整数解$(x,y)$のうち，$x$が正の整数で最小になるものを求めよ．

$2$以上の自然数$n$について$n!!$は累乗数にならないことを示せ．

$2023!!$が$5$で割り切れる最大の回数を求めよ．

($2023!$が$2$で割り切れる最大の回数)が$2$で割り切れる最大の回数を求めよ．

$2023$と互いに素な$2023$以下の自然数の和を求めよ．

$\displaystyle\sum_{n=1}^{2023}gcd(n,2023)$を求めよ．

2023年で(月の数字)(日の数字)を順番に並べた数が平方数となる日は何日あるか．

2023年で(月の数字)(日の数字)を順番に並べた数が回文数となる日は何日あるか．

2023年で(月の数字)(日の数字)を順番に並べた数が$11$の倍数となる日は何日あるか．

2023年で(月の数字)$|$(日の数字)となる日は何日あるか．

$(\sigma(n))^2=\sigma ^2(n)$を満たす正整数をすべて求めよ．

一日の各分において，正確なアナログ時計の長針と短針の間の角度(小さい方)をすべて足し合わせた値は何度か．

長方形の3辺$x,y,z$が$xy+yz+zx=2023$を満たしているとき，長方形の体積の最小値を求めよ．

$p$が素数であるような正整数の組$(a,b,p)$であって，$a^p-b!!=p$を満たすものをすべて求めよ．

2023年の中で土日が最も多い月はどれか．

$\phi(n)=n!!$を満たす正整数$n$をすべて求めよ．

$\displaystyle\sum_{n=1}^{2023}lcm(n,2023)$を求めよ．

底面の半径が$n$，高さが$2n$の円錐がある．この円錐を底面に平行な一致しない$2a-1$個の平面ですべての円錐台・円錐の高さが同じになるように切断する．($a\in\mathbb{Z_{++}}$)
次に$2a$個の物体のうち下から数えて奇数番目のものを順番はそのまま，円錐台の上面の内部にその上の円錐台の下面が完全に含まれるように置く．偶数番目のものも同様に行う．
このときできた2つの立体の体積と表面積の比を求めよ．

平面を放物線で分割するとき，最大でいくつの領域に分割されるか．

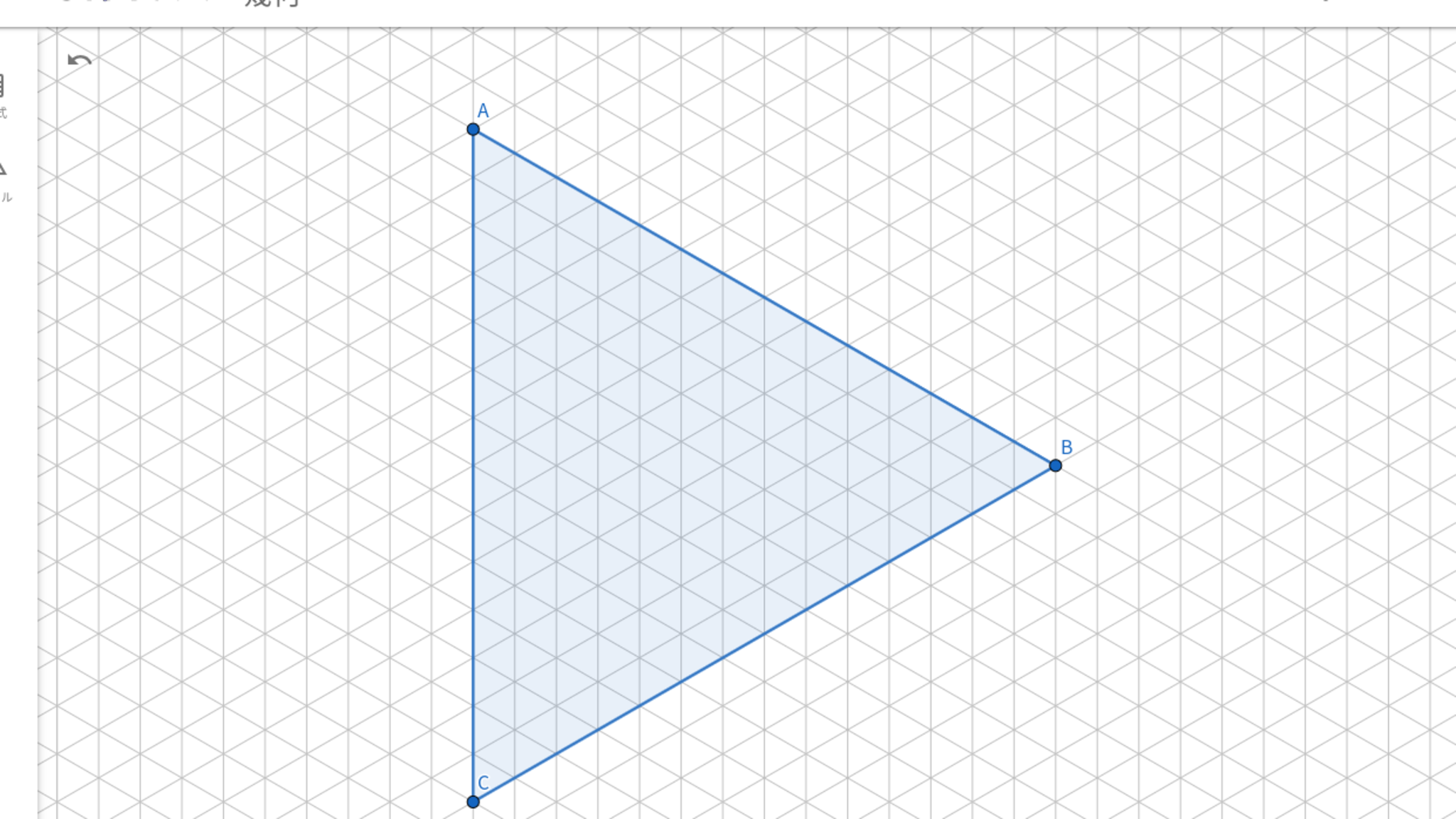
図のように一辺$14$の正三角形があり，辺と平行な直線が間隔$1$おきに引かれている．この直線の交点を三角格子点と呼ぶこととする．
この三角格子点上に$3$点$A,B,C$を配置することを考えます．$3$点は直線上を通ってのみ移動することが出来ます
以下が成り立つような$m$の最小値を求めよ．
　　　　　正三角形の内部(辺上も含む)の三角格子点全ての点$P$において，点$A,B,C$のいづれかが移動距離$m$以内で点$P$に移動する事ができるような点$A,B,C$の配置が存在する．
0.6666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666

円の内部を円で分割するとき，最大でいくつの領域に分割されるか．

円の内部を楕円で分割するとき，最大でいくつの領域に分割されるか．

平面を放物線で分割するとき，最大でいくつの領域に分割されるか．

楕円の内部を円で分割するとき，最大でいくつの領域に分割されるか．

楕円の内部を楕円で分割するとき，最大でいくつの領域に分割されるか．

平面を線分で分割するとき，最大でいくつの領域に分割されるか．

空間を楕円体で分割するとき，最大でいくつの領域に分割されるか．

$3^x-8^y=2xy-1$を満たす正整数の組$(x,y)$をすべて求めよ．

空間を回転放物面で分割するとき，最大でいくつの領域に分割されるか．

球の内部を球で分割するとき，最大でいくつの領域に分割されるか．

空間を面積が有限である長方形の平面で分割するとき，最大でいくつの領域に分割されるか．

空間を高さが無限である円柱で分割するとき，最大でいくつの領域に分割されるか．

軸が$60°$で交わり，半径がともに$1$，高さが無限である$2$つの円柱の共有部分の体積を求めよ．

軸がそれぞれ$x,y,z$軸で，半径がともに$1$，高さが無限である$3$つの円柱の共有部分の体積を求めよ．

$100$をどの2つも互いに素でない$2$つの自然数の和で表す方法は何通りか．

$2023$以下の正整数のうち，正の約数を$6$個持つ数はいくつあるか．

$2023$との差の絶対値が最も小さい素数を求めよ．

$2023$との差の絶対値が最も小さい平方数を求めよ．

$2023$との差の絶対値が最も小さい三角数を求めよ．

面積が$2023$，3辺の長さがすべて整数である三角形はいくつあるか．

リュカ数かつ平方数である数をすべて求めよ．

ぴー君は
　　　　　 うんたらかんたら
　　　　　あなたの好きな自然数$n$を一つ決めて$g(n)$をこの設問におけるあなたの得点とする．
という問題を解いた．
その後，ぴー君は$g(1)=g(2)=\cdots=g(5)=0$だったことから以下の問題を考えた
正整数の定数$m$と$3$以上の自然数$n$に対して$f(n)=\displaystyle\sum_{k=1}^mk^n$とおく．
$f(1)\equiv f(2)\equiv\cdots\equiv f(n-2)\equiv0(modm)$を満たす正整数$m$の必要十分条件を求めよ．

ぴー君は
　　　　　円周率が$3.05$よりも大きいことを証明せよ．
という問題に対して円の中に正十二角形を内接し，周長比較で示した．
その後，ぴー君はもっと厳しい評価もできると考えた．
ぴー君の証明方法では$\pi >x$まで証明できる．$x$の最大値の小数第$4$位以下を切り捨て，小数第$3$位までで答えよ．

フィボナッチ数かつ$2$冪である数をすべて求めよ．

無理数の無理数の無理数乗乗は無理数か．