Projective Geometry @ a view point of Harmonicness

Projective Geometry @ a view point of Harmonicness

Introduction to Cross-ratio: Geometric meaning

The concept of Cross-ratio appears as introduction in many books of projective geometry. For example, Cremona's Elements of Projective Geometry, Bertini's Book, and so on. There is a book for this topic. Cross-ratio is important since this value gives complete invariance between projective ranges of four points. Harmonicness has a geometrical speciality for plane projective geometry.
We introduce to projective geometry at a view point of Cross-ratio, especially Harmonicness.

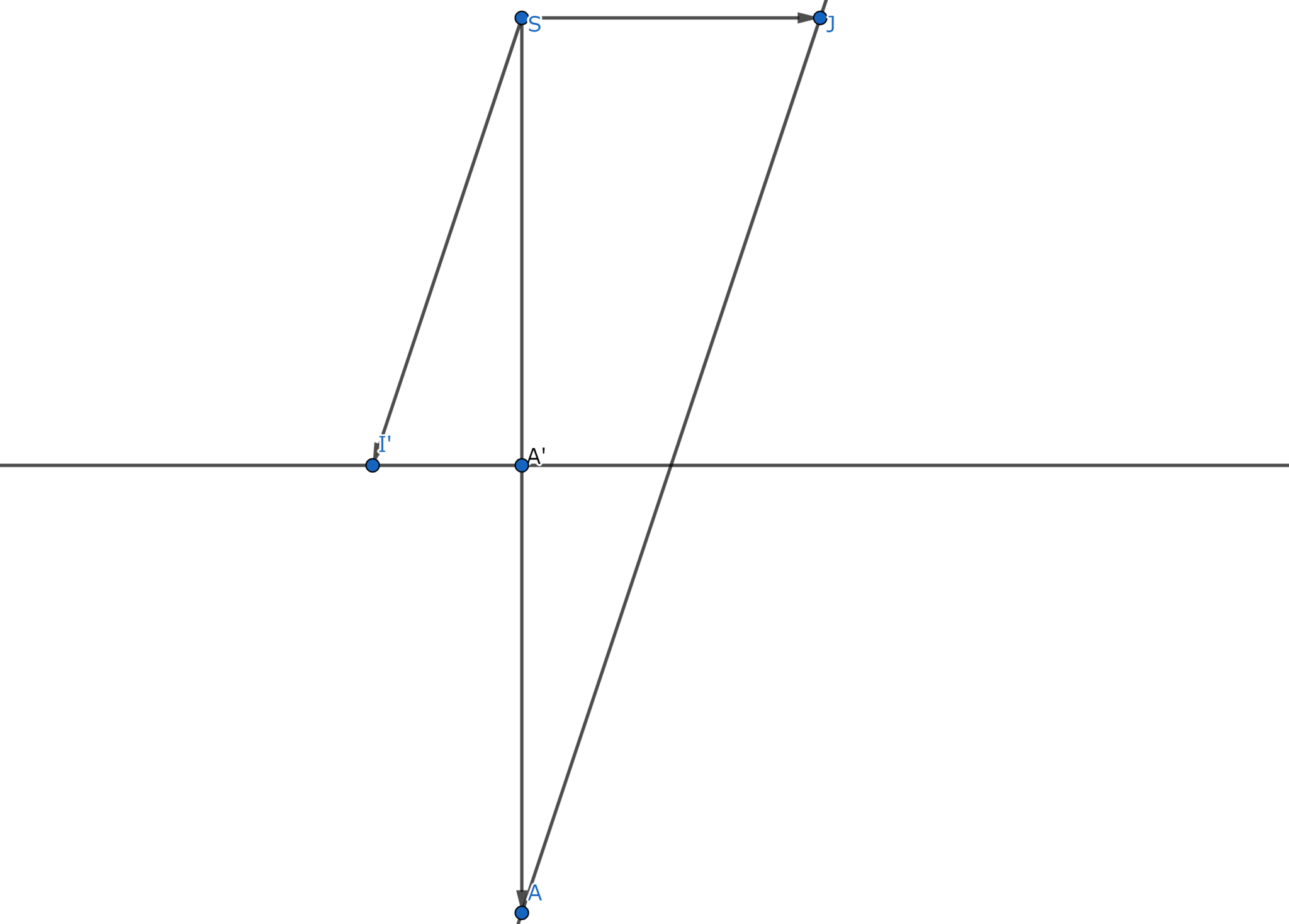Similar triangles
We condider the above picture in a plane.
By the similarity of two triangles $ SAJ,A'SI'$, $ JA/JS = I'S/I'A' $ hence $ JA.I'A' = JS.I'S .$ For another perspective points $ B,B'$ similarly we have $ JB.I'B' = JS.I'S$. So we get $$ JA.I'A' = JB.I'B' .$$ Therefore this value does not depend on the choices of two perspective points.
Let $ k$ be this constant value. Then, $$ AB = JB - JA = k/I'B' - k/I'A' = k.(I'A'-I'B')/I'A'.I'B' = k.B'A'/I'A'.I'B'.$$
Take two other perspective points $ C,D$.
Calculate the ratio $$ AC/BC:AD/BD = A'B'/B'C':A'D'/B'D'.$$
This constant ratio for perspectivity is called Cross-ratio.

Definition of Cross-ratio

Elementary form

$$ (ABCD) = AC/BC : AD/BD $$
where $ A,B,C,D $ are four different points on a projective line, and $ XY $, for two points $ X,Y $ means the distance from $ X$ to $ Y$.
Notice that the distance $ XY$ includes the signs. This means that if the points $ X,Y$ are at finite distance we are on some affine line of the projective line with direction. (Projective lines can not be directed.)
Cross-ratio does not depend on the choices of direction since the ratios $ AC/BC$ and $ AD/BD$ are not affected their values.

Coordinated form

$$ (\lambda_1\lambda_2\lambda_3\lambda_4)= |\lambda_1\lambda_3|/|\lambda_2\lambda_3|:|\lambda_1\lambda_4|/|\lambda_2\lambda_4|$$
where $ \lambda_1,\lambda_2,\lambda_3,\lambda_4$ are four different homogeneous coordinates on a projective line, and $ |\lambda \mu|$ indicates the determinant of the vectors of $ \lambda, \mu$.

Fundamental Properties

Invariance on perspectivity

As we see in the introduction, the value of cross-ratio does not depend on perspectivity. Another proof can be found at coordinated form: The perspectivities are mobius transformations so tansform the coordinates by nonsingular matrix $M$ we get
$$ |M\lambda_1M\lambda_i|/|M\lambda_2M\lambda_i| = |M(\lambda_1\lambda_i)|/|M(\lambda_2\lambda_i)| = |M||\lambda_1\lambda_i|/|M||\lambda_2\lambda_i| = |\lambda_1\lambda_i|/|\lambda_2\lambda_i|.$$
for $i=3,4$.

Complete Invariance on projectivity

Completeness is given by two properties:

• Two ranges which consist of three points respectively are projective.
• Uniqueness of fourth point of a range under a fixed value of cross-ratio.

Give two pairs $A,B,C,D; A',B',C',D'$ of four points resp which have same value of cross-ratio. Since two ranges of three points resp. are projective, we may assume that two ranges are perspective. Then, we can find a point $D''$ in the same line of points $A'B'C'$ by taking the perspectivity D to the line. As perspectivity holds the invariance, we have $(ABCD) = (A'B'C'D'')$. But, by assumption $(ABCD)=(A'B'C'D')$, $(A'B'C'D') = (A'B'C'D'')$. Hence $D'=D''$ as uniqueness of the fourth point under given value of cross-ratio. Therefore we obtain that $A,B,C,D$ and $A'B'C'D'$ are perspective. Taking operations of perspectivities the claim holds: if $A,B,C,D$ and $A',B',C',D'$ are equi-harmonic then they are projective.

Other properties

We note other properties without proofs.
$$(ABDC) = 1/(ABCD)$$
$$(ACBD) = 1-(ABCD)$$
$$(ACDB) = -1/(ABCD)$$
where their values are condidered on some affine line.

Harmonicness

Definition

Geometric

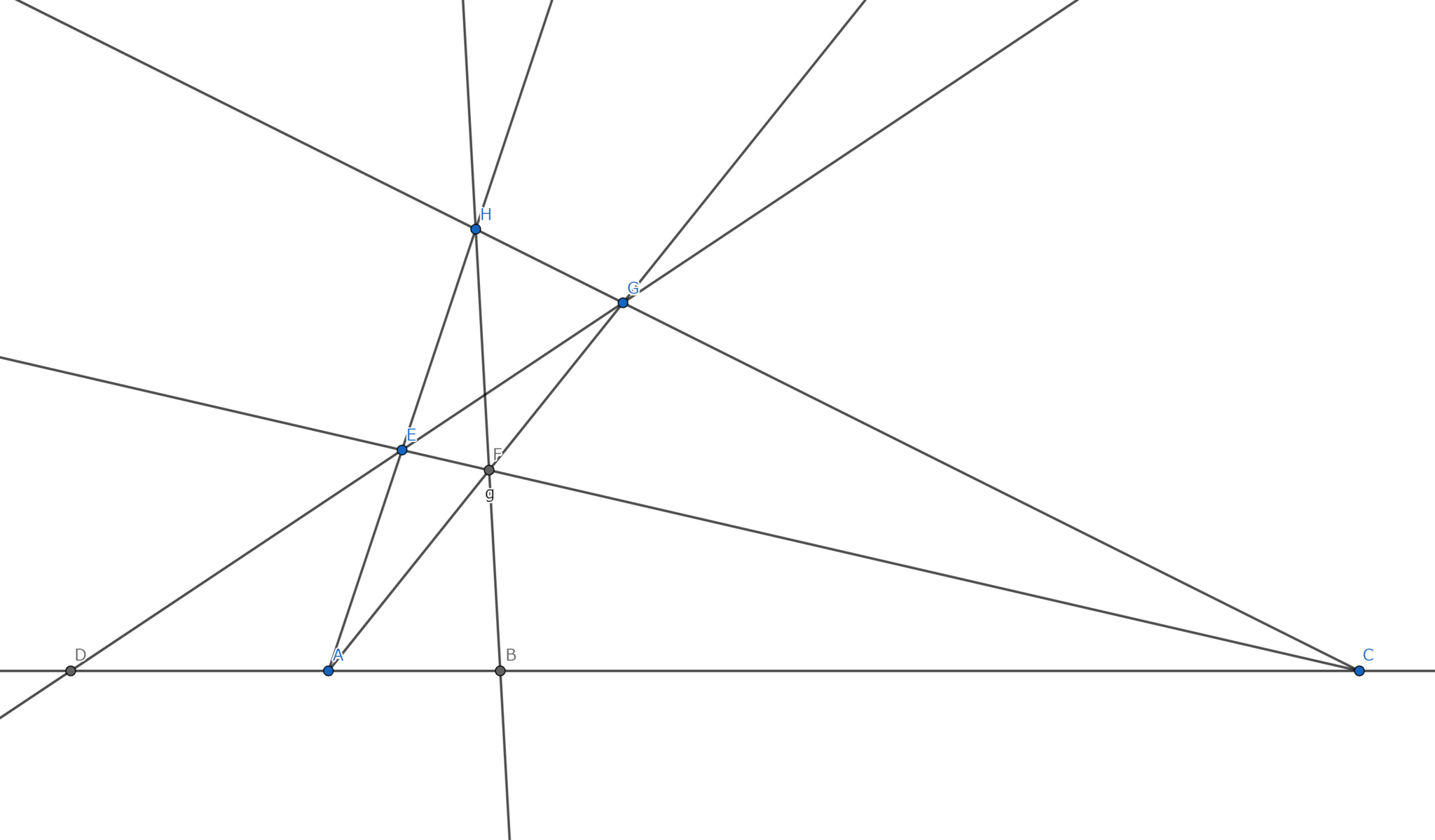Harmonic range
Give four different points $A,B,C,D$ on a line in the plane (see the above picture).
When we draw two lines from the point $A$ and also two lines from the point $C$ we have a rectangle $EFGH$ whose two pairs of diagonals are $EG$ and $FH$ respectively. Futher if drawing two lines along the diagonal pairs the lines intersect at the points $B,D$ on the line $AC$ respectively, we say the points $A,B,C,D$ are harmonic.
Notice that the definition does not ask the choices of every two lines from $A,C$.

Cross-ratio

If the cross-ratio of four different coordinates $\lambda_1,\lambda_2,\lambda_3,\lambda_4$ are given on the line and
$$ (\lambda_1\lambda_2\lambda_3\lambda_4)= |\lambda_1\lambda_3|/|\lambda_2\lambda_3|:|\lambda_1\lambda_4|/|\lambda_2\lambda_4| = -1:1$$
then we call they are harmonic.

Properties

Equivalence of Definitions

Since any range of three points is projective to the range of three points which are positioned at $(-1:1),(1:1),(0:1)$ respectively, it is suffice to show the equivalence for the range of four points $(-1:1),(1:1),(0:1),D$.

Assume that they are harmonic in the geometric meaning. Draw a vertical line from the point $(0:1)$ and two pairs of two lines from $(-1:1),(1:1)$ to be intersected at two points in the vertical line of the same side. Then the line passing through the point $D$ must be horizontal, hence $D$ is the point of infinity $(1:0)$.
Now, calculate the cross-ratio:
$$((-1:1)(1:1)(0:1)(1:0)) = |\begin{bmatrix} -1 & 0 \\ 1 & 1 \\ \end{bmatrix}| / |\begin{bmatrix} 1 & 0 \\ 1 & 1 \\ \end{bmatrix}| : |\begin{bmatrix} -1 & 1 \\ 1 & 0 \\ \end{bmatrix}| / |\begin{bmatrix} 1 & 1 \\ 1 & 0 \\ \end{bmatrix}| = -1/1:-1/-1 = -1:1. $$
Therefore, harmonicness in the geometric meaning is harmonicness in the cross-ratio.

Conversely, we assume that the range is harmonic in the cross-ratio, i.e., $((-1:1)(1:1)(0:1)(\lambda_4:\lambda_4')) = -1/1 : -(\lambda_4'+\lambda_4)/(\lambda_4'-\lambda_4) = -1:1$. Then as it become a linear equation so the fourth coordinate uniquely determined and $(\lambda_4:\lambda_4') = (1:0)$.
Now ,we must verify the geometric definition but it is suffice to show the case that the line from $(0:1)$ is vertical because if it is not vertical then projecting the range fixing the $(0:1)$ we obtain a range $(-t:1),(0:1),(t:1),(1:0) (t\not=0)$ and the line which the range lies and is vertical and whose cross-ratio is still $-1:1$. Then, the line passing through the point $(1:0)$ is horizontal in any way. Therefore, harmonicness in the cross-ratio is harmonicness in the geometric meaning.

Equation

Let $M,O,A_1,A_2$ be four different points on a line, and assume they are harmonic.
From the hamonicness we have an equation $MA_1/OA_1+MA_2/OA_2 = 0$. Taking $MA_i = MO+OA_i$ and dividing by $MO$, we obtain
$$(1/OM-1/OA_1)+(1/OM-1/OA_2) = 0.$$

Generalizing harmonicness

When we consider "Harmonicness" for arbitrary many points of a sequence, we can generalize the already known harmonicness by gaining the sum:
Fix two points $M,O$ and let $A_i (i=1,...,n)$ be $n$ different points on a line. We define harmonicness of the points $A_1,...,A_n$ by the following equation:
$$\sum_{i=1,...,n} (1/OM - 1/OA_i) = 0.$$

We can more generalize this:
$$\sum_{\#I=r,I\subseteq\{1,...,n\}}\prod_{i\in I} (1/OM - 1/OA_i) = 0.$$

Comments for this description

Elementary form of Cross-ratio is introduced in Elements of Projective Geometry written by Cremona. The invarience of cross-ratio appears in many books of projective geometry but the complete invariance appears only in this EPG, not does in other references.
The equations of generalized harmonicness are in papers of Boncelet, Jonquieres, Cremona. The former equation is introduced by Poncelet at first and the latter equation is introduced by Jonquires at first.