競技数学解説

数学オリンピック2023予選解説 1~8編 (JMO2023)

数学オリンピック,JMO2023予選解答解説,JMO

34724

はじめに

2023/1/9に実施された数学オリンピックの1~8の解説をしたいと思います.受験された方はお疲れ様でした。数学オリンピック楽しいよー！ということを布教すべく解説記事を書いてみます.それではよろしくお願いします.

本記事の回答が必ずしも最短,正攻法であるとは限りません.

解説

JMO2023-1

$10$ を足しても $10$ をかけても平方数となる最小の正の整数を求めよ.

ポイント：落ち着いて立式する

求める正の整数を $n$ とおきます.まず, $10$ をかけても平方数となることから $n$ は $10$ の倍数です.従って, $n = 10 n^{' 2}$ と置くことができます. $10 n^{' 2} + 10$ が平方数となるような最小の $n^{'}$ を求めれば良いことになります.小さい数から順に調べていくと $n^{'} = 3$ を得ます.従って, $n = 10 \cdot 3^{2} = 90$ となります.

答： $90$

JMO2023-2

$2$ の方が $3$ より多く各桁に現れるような正の整数を"良い数"と呼び, $3$ の方が $2$ より多く各桁に現れるような正の整数を"悪い数"と呼ぶ.たとえば, $2023$ には $2$ が $2$ 回, $3$ が $1$ 回現れるので, $2023$ は"良い数"であり, $123$ には $2$ が $1$ 回, $3$ が $1$ 回現れるので, $123$ は"良い数"でも"悪い数"でもない. $2023$ 以下の"良い数"の個数と"悪い数"の個数の差を求めよ.

ポイント：求める数が差であることに着目する

"良い数"と"悪い数"の個数をそれぞれ求めてその差を計算しても良いですが,もう少し賢く解くことができます.一桁の"良い数"と"悪い数"の個数は対称的なので等しいです.同様に二桁,三桁,千番台の四桁の"良い数"と"悪い数"の個数は対称的なので等しいです.従って, $2000$ ~ $2023$ までを調べれば十分であることがわかります.全て書き出すと, $22$ 個となります.

答: $22$ 個

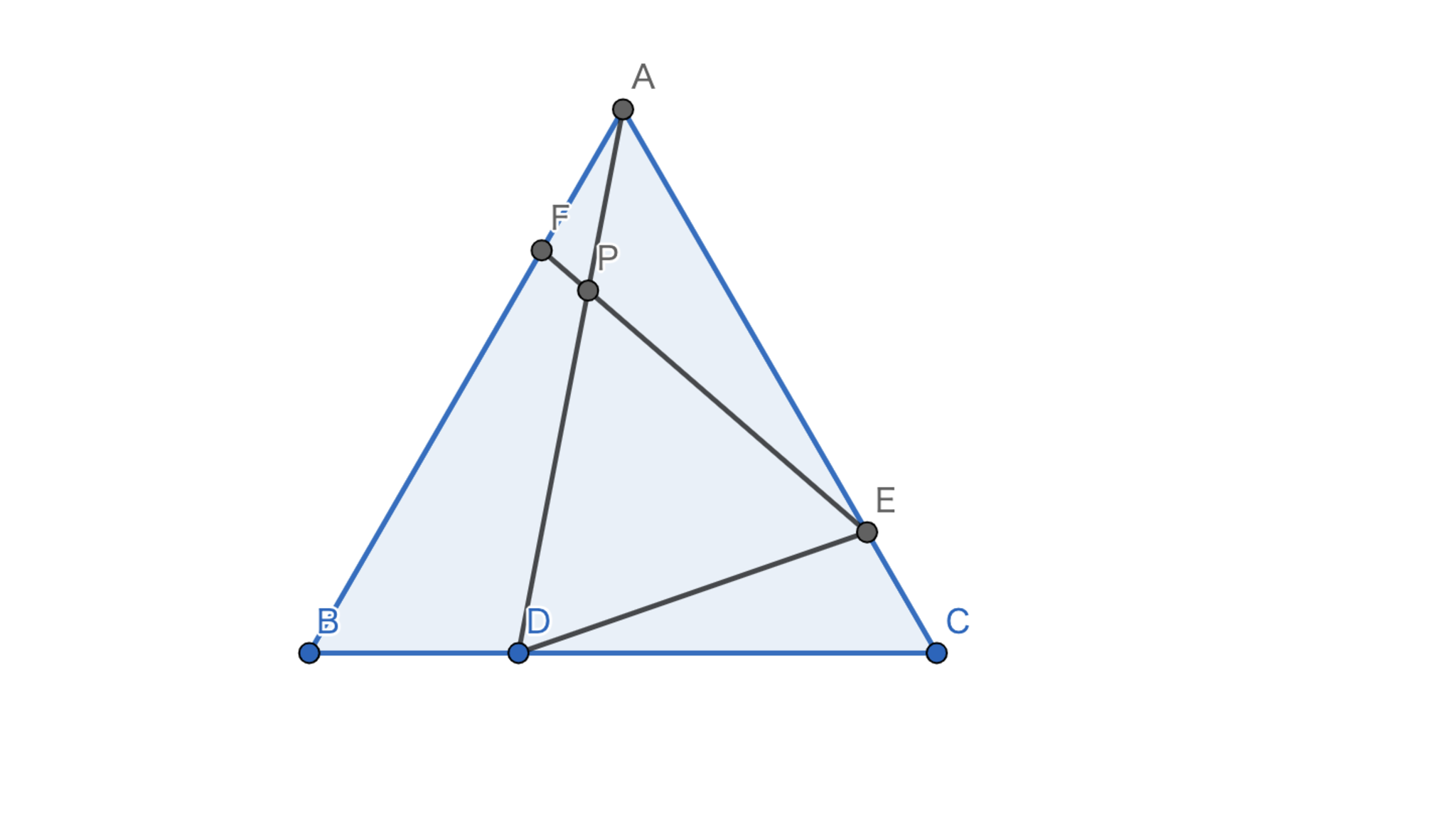
JMO2023-3

一辺の長さが $3$ である正三角形 $A B C$ の辺 $B C, C A, A B$ 上にそれぞれ点 $D, E, F$ があり, $B D = 1$ , $∠ A D E = ∠ D E F = 60 °$ をみたしている.このとき,線分 $A F$ の長さを求めよ.

ポイント:相似を発見する

最終的に $A F$ の長さを求めたいのでそれを含む $△ A F P$ に注目します.簡単な角度計算により $△ A F P ∽ △ D E C$ であるとわかります.従って, $A F : A P = D E : D C$ を得ます. $△ P D E$ が正三角形なのでその一辺の長さを $x$ とおけば $A F : A D - x = x : 2$ となります.さらに,余弦定理より $A D = \sqrt{7}$ なので $A F : \sqrt{7} - x = x : 2$ となります.よって, $x$ を求めれば良いことになります.ここで, $△ A D C ∽ △ A E D$ であるので $A C : D C = A D : E D ⟺ 3 : 2 = \sqrt{7} : x$ を得ます.よって, $x = \frac{2 \sqrt{7}}{3}$ となります.以上より, $A F = \frac{7}{9}$ を得ます.

答: $\frac{7}{9}$

JMO2023-3

JMO2023-4

正の実数 $x, y$ に対し,正の実数 $x * y$ を $x * y = \frac{x}{x y + 1}$ で定める.この時,

(((\dots (((100 * 99) * 98) * 97) * \dots) * 3) * 2) * 1

を計算せよ.ただし解答は

*

を用いずに数値で答えること.

ポイント:うまく計算できるようになっているのだろうと考える

$f (n, a) = (((\dots (((n * (n - 1)) * (n - 2)) * (n - 3)) * \dots) * (a + 1)) * a$ とおきます.(求める数は $f (100, 1)$ )

まともに,100回計算するのは流石にきついですね.どうにかうまいこと計算できるようになっているはずなので問題文の $100$ を $2, 3, 4$ 程度の小さな数に変更して実験してみます.

①

n = 2

の場合

2 * 1 = \frac{2}{3}

②

n = 3

の場合

(3 * 2) * 1 = \frac{3}{7} * 1 = \frac{3}{10}

③

n = 4

の場合

((4 * 3) * 2) * 1 = (\frac{4}{13} * 2) * 1 = \frac{4}{21} * 1 = \frac{4}{25}

これらの実験から $f (n, a) = \frac{1}{\frac{1}{n} + a + (a + 1) + (a + 2) + \dots + (n - 1)}$ と予想が立ちます.これを示します.

$f (n, a + 1) = \frac{1}{\frac{1}{n} + (a + 1) + (a + 2) + (a + 3) + \dots + (n - 1)}$ と仮定します.(これは $a = n$ の時正しい.)
$f (n, a) = f (n, a + 1) * a = \frac{\frac{1}{\frac{1}{n} + (a + 1) + (a + 2) + (a + 3) + \dots + (n - 1)}}{a \cdot \frac{1}{\frac{1}{n} + (a + 1) + (a + 2) + (a + 3) + \dots + (n - 1)} + 1} = \frac{1}{\frac{1}{n} + a + (a + 1) + (a + 2) + (a + 3) + \dots + (n - 1)}$ となるので帰納法より示されました.よって,答えは $\frac{100}{495001}$ となります.

答: $\frac{100}{495001}$

エレガントな別解

エレガントな別解があるので紹介します.
$(x * y) * z = \frac{x}{x y + 1} * z = \frac{x}{x z + x y + 1} = x * (y + z)$ であるので与式は $100 * (1 + 2 + 3 + \dots + 99) = \frac{100}{495001}$ となります.

答: $\frac{100}{495001}$

JMO2023-5

$a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}, a_{7}$ を相異なる正の整数とする.数列 $a_{1}, 2 a_{2}, 3 a_{3}, 4 a_{4}, 5 a_{5}, 6 a_{6}, 7 a_{7}$ が等差数列であるとき, $| a_{7} - a_{1} |$ の最小値を求めよ.

ポイント:公差を $d$ とおく

公差を $d$ とおくと, $k a_{k} = a_{1} + (k - 1) d$ となります.この時,求める $| a_{7} - a_{1} | = \frac{6}{7} | (d - a_{1}) |$ となります. $a_{k} = \frac{a_{1} + (k - 1) d}{k} \in Z$ であるから, $a_{1} + (k - 1) d \equiv 0 (\mod k)$ ,すなわち $a_{1} \equiv d (\mod k)$ を得ます. $k$ は $1$ ~ $7$ までの値をとるから, $1, 2, 3, 4, 5, 6, 7$ の最小公倍数 $420$ を用いて $a_{1} \equiv d (\mod 420)$ と表せます. $d = a_{1}$ とすると,「相異なる」という条件に反するので $d \neq a_{1}$ です.従って, $| (d - a_{1}) |$ の最小値は $420$ となります. $a_{k} = \frac{420}{k}$ とすれば実際にそのような構成は可能なので解答は $360$ となります.

答: $360$

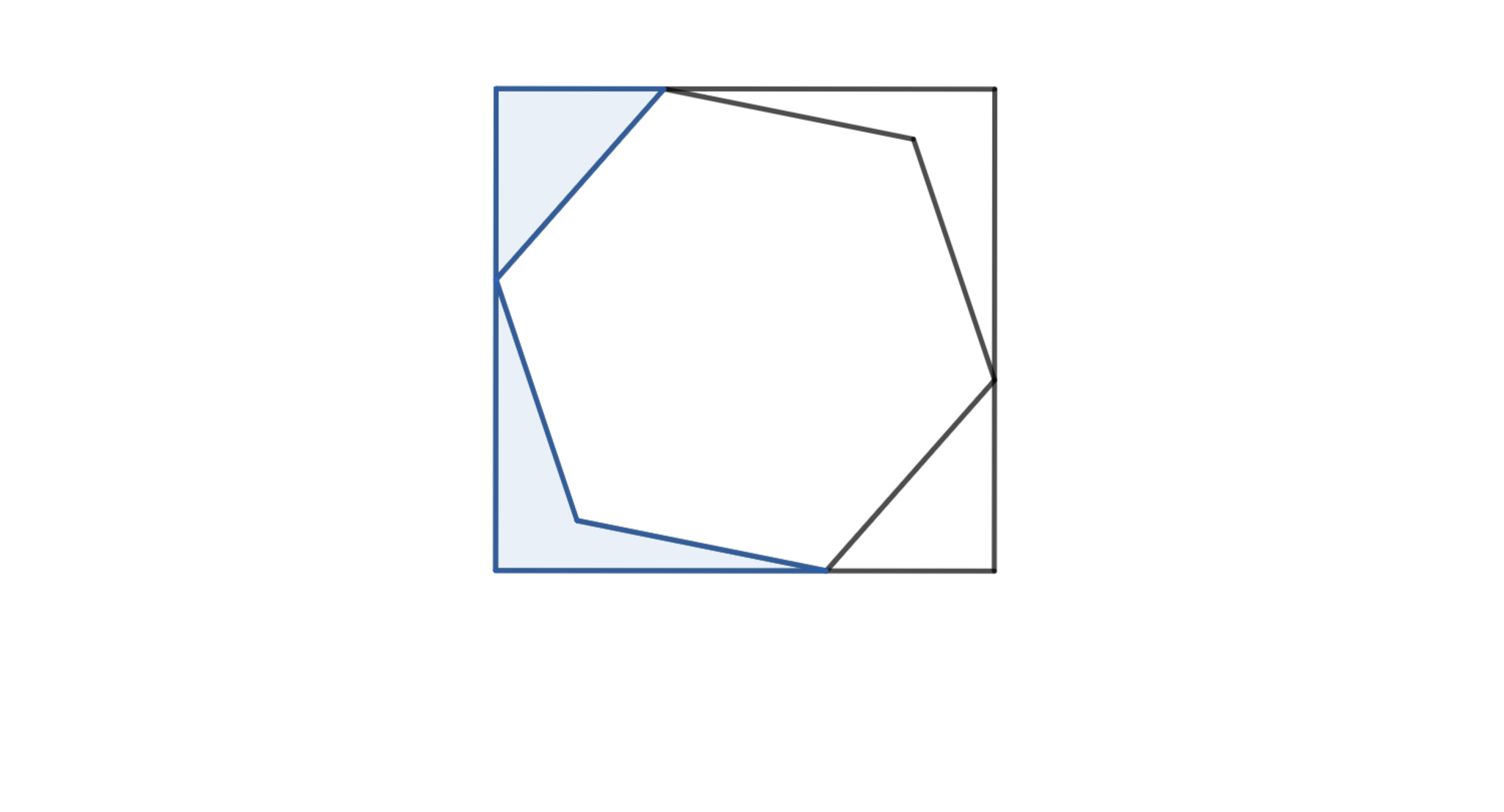
JMO2023-6

正六角形が図のように長方形に内接している.斜線部の三角形と四角形の面積がそれぞれ $20, 23$ である時,正六角形の面積を求めよ.

JMO2023-6

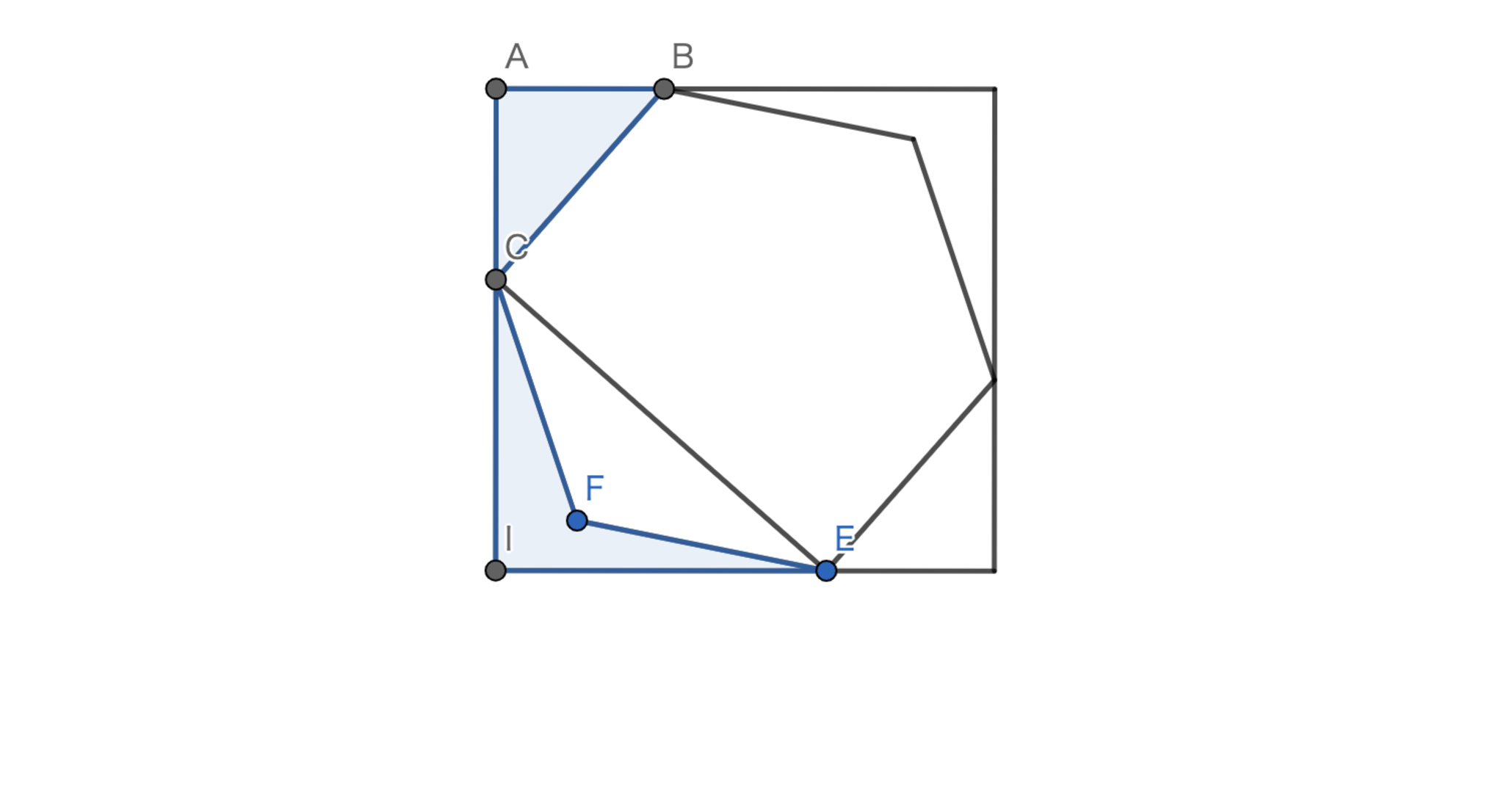
ポイント：具体的な辺の長さを出すのは難しそうなので相似などで面積の関係を考える

求める面積を $S$ とし,下図のように点に名前をつけます.簡単な角度計算より $△ A B C ∽ △ I C E$ であり, $B C$ と $C E$ の辺の比を考えればその相似比は $1 : \sqrt{3}$ であるから面積比は $1 : 3$ である.よって, $△ I C E = 60 = 23 + △ C F E$ であるから $△ C F E = 37$ を得る. $△ C F E = \frac{1}{6} S$ であるから $S = 222$ を得ます.

答: $222$

JMO2023-6(2)

JMO2023-7

正の整数 $a, b, c$ は

\frac{(a b - 1) (a c - 1)}{b c} = 2023, b \leq c

をみたしている.

c

としてありうる値を全て求めよ.

ポイント：不等式で評価する

$\frac{(a b - 1) (a c - 1)}{b c} = (a - \frac{1}{b}) (a - \frac{1}{c}) = 2023$ となる. $a - 1 \leq a - \frac{1}{b}, a - \frac{1}{c} < a$ であることから $a = 45$ を得ます. $b = 1$ の時,実際に代入してみると不適であるとわかります.従って, $b \neq 1$ となります. $b, c$ が共に $1$ でないならば $a b - 1$ は $b$ の倍数とはならないため $\frac{a c - 1}{b} \in Z$ となります.同様に $\frac{a b - 1}{c} \in Z$ となります.

$a c = b k + 1, a b = c l + 1$ とおきます( $k \geq l$ ).すると $k l = 2023$ を得るので $(l, k) = (1, 2023), (7, 17^{2}), (17, 7 \cdot 17)$ となります. $a = 45$ と併せて連立方程式を解くと, $c = 82, 167, 1034$ を得ます.

答: $82, 167, 1034$

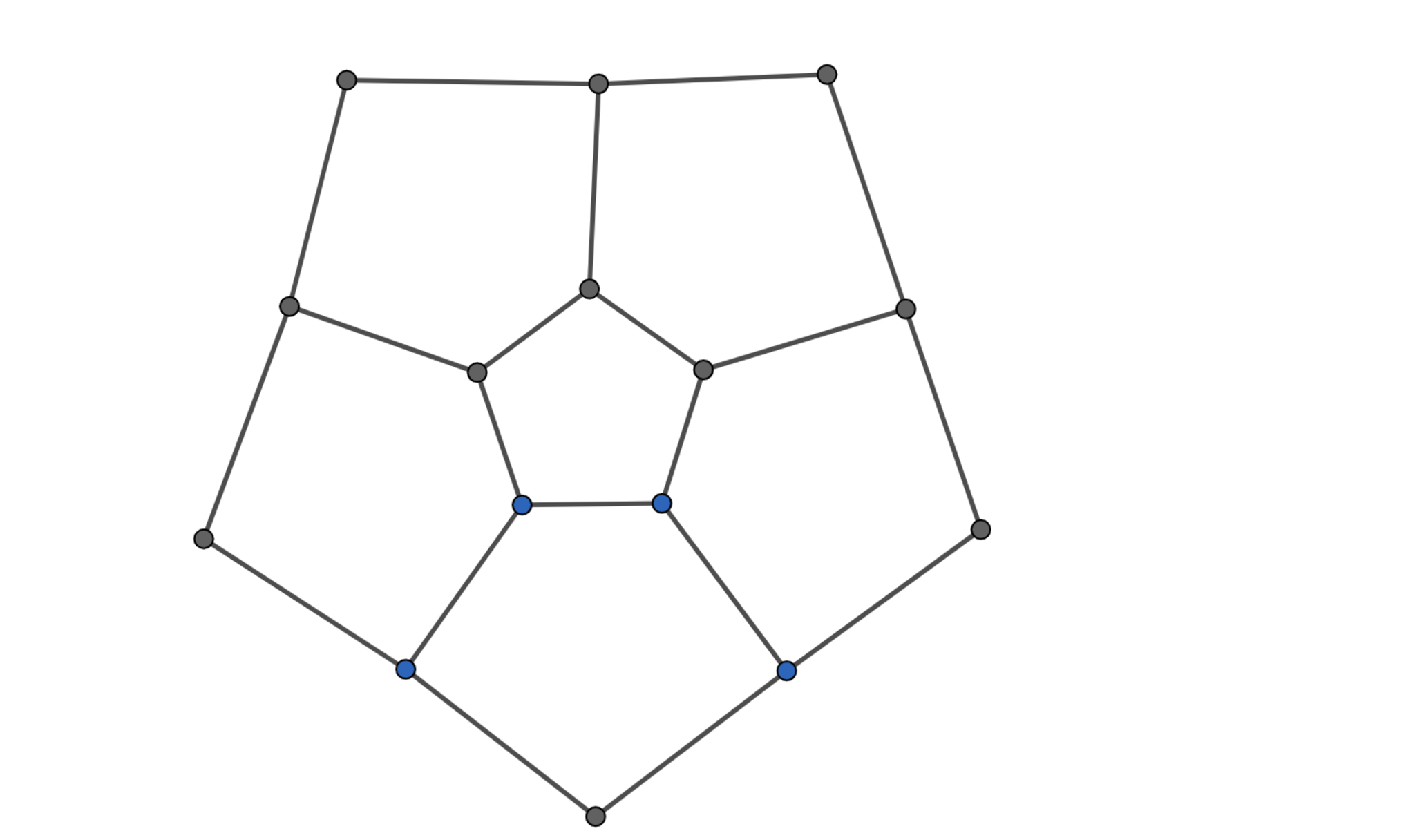
JMO2023-8

図のような $15$ 個の円と $20$ 本の線分からなる図形があり,これらの円のそれぞれに $0, 1, 2$ のいずれかを $1$ つずつ書き込むことを考える.書き込み方の"美しさ"を, $20$ 本の線分のうち,その両端の円に書き込まれた数の差が $1$ であるようなものの個数とする."美しさ"としてありうる最大の値を $M$ とするとき,"美しさ"が $M$ となるような書き込み方は何通りあるか.

JMO2023-8

ポイント:実験をして $M$ のアタリをつける.

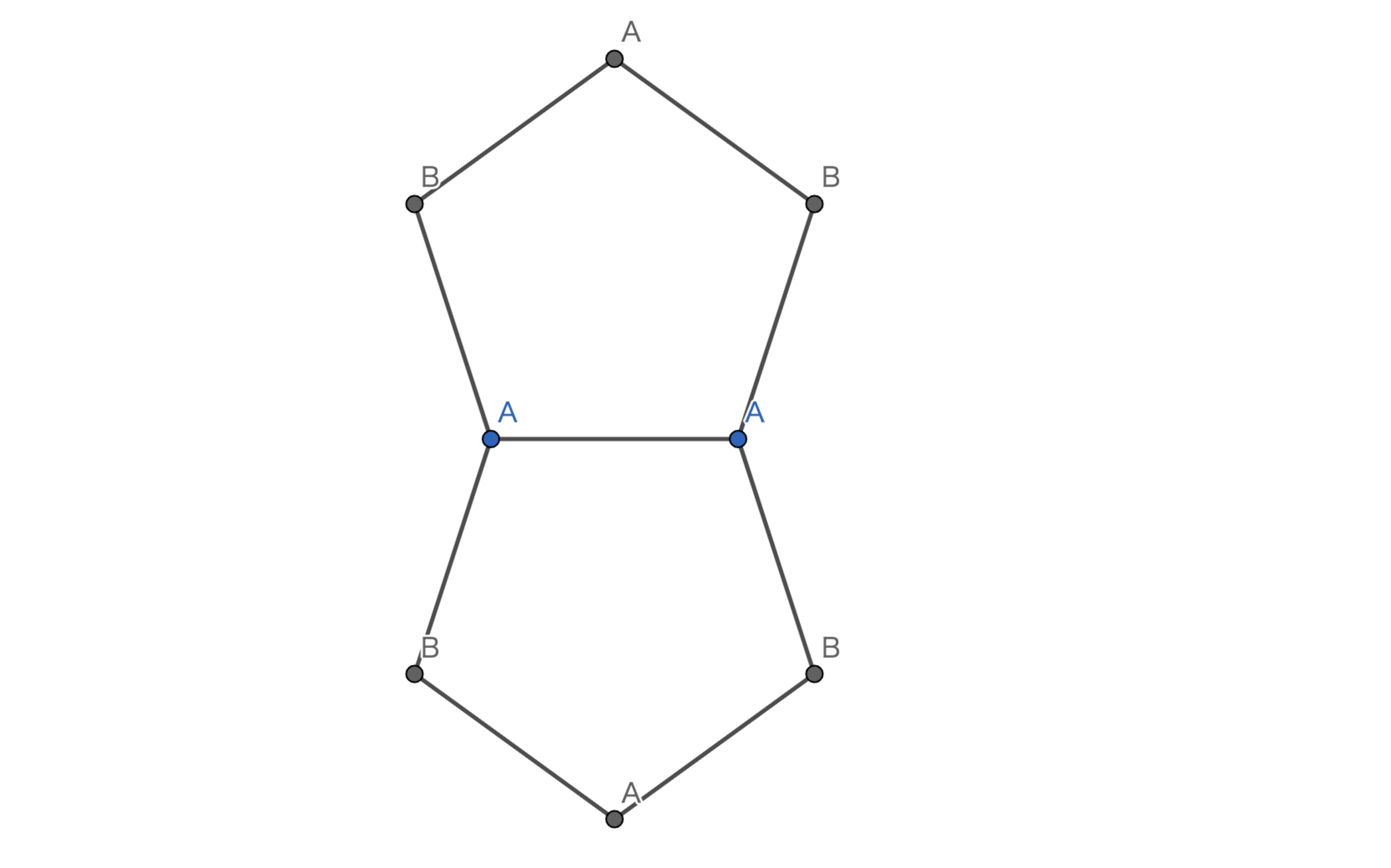
たくさん実験すると, $M = 17$ までは作れることがわかると思います.よって,暫定的に $M \leq 17$ であることを証明してみます.下図のような五角形が二つつながった図形を考えてみましょう.このような図形において,美しさが $9$ となるように書き込むのは不可能であることは容易にわかります.一方で美しさを $8$ とすることは可能です(図を参照).従って,五角形が二つ存在した時に美しくない辺(その両端の円に書き込まれた数の差が $1$ でない線分)は必ず一つ存在します.問題の図に戻ると,五角形は $6$ つあるから最低限美しくない辺が $3$ つ(すなわち $M \leq 17$ )は必要です.美しさを $17$ とすることは可能なので $M = 17$ となります.

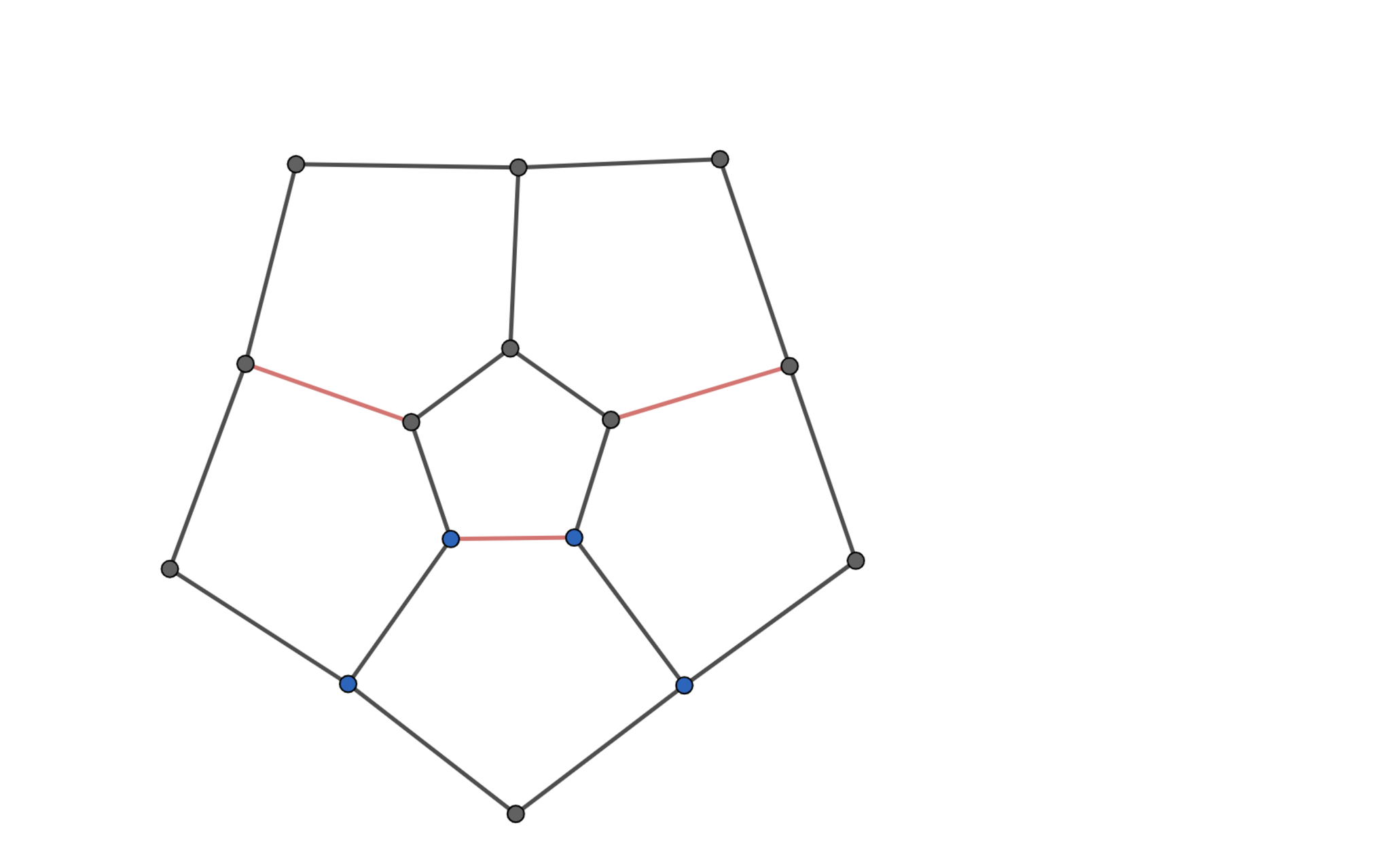
$M = 17$ とわかったので数え上げていきます.中央の五角形は必ず一つ美しくない辺を持ちます.そのような辺の選び方は $5$ 通りです.中央の五角形の美しくない辺が決まれば残りの美しくない辺も決まります.よって,美しくない辺の配置は $5$ 通りです.各 $5$ 通りに対してそれぞれ対称なので代表して下図のような状況を考えます.赤く色をつけた辺が美しくない辺です. $A$ を $1$ , $B$ = $0 o r 2$ とします.( $0$ と $2$ は等価です.)

内側の正五角形の美しくない辺の両端の円に書かれている数字がAかBで場合分けをしましょう.そこを定めてしまえば,残りの円に書かれる数字がAなのかBなのかが定まります.それぞれAに書き込まれる数の候補は $1$ 通り,Bに書き込まれる数の候補は $2$ 通りなのでBの円の数を $x$ とすれば書き込み方は $2^{x}$ となります.それぞれのケースについて $x = 7, 8$ なので求める場合の数は $5 (2^{7} + 2^{8}) = 1920$ が解答となります.