JMO2023予選の10番のみ
こんにちは, 1週間後に†高校受験†が控えている中3のVecです. なので今回のJMOには参加していませんが, 大会後出回っていた問題を見て珍しく難角問題だった10番のみ解いてみたので解説を書いています~
鋭角三角形$ABC$があり, $A$から辺$BC$に下した垂線の足を$D$, 辺$AC$の中点を$M$とする.
線分$BM$上に点$P$を, $\angle PAM = \angle BAM$を満たすように取る. $\angle BAP = 41 ^\circ, \angle PDB = 115^\circ$のとき, $\angle BAC$の大きさを求めよ.
図はこんな感じです.
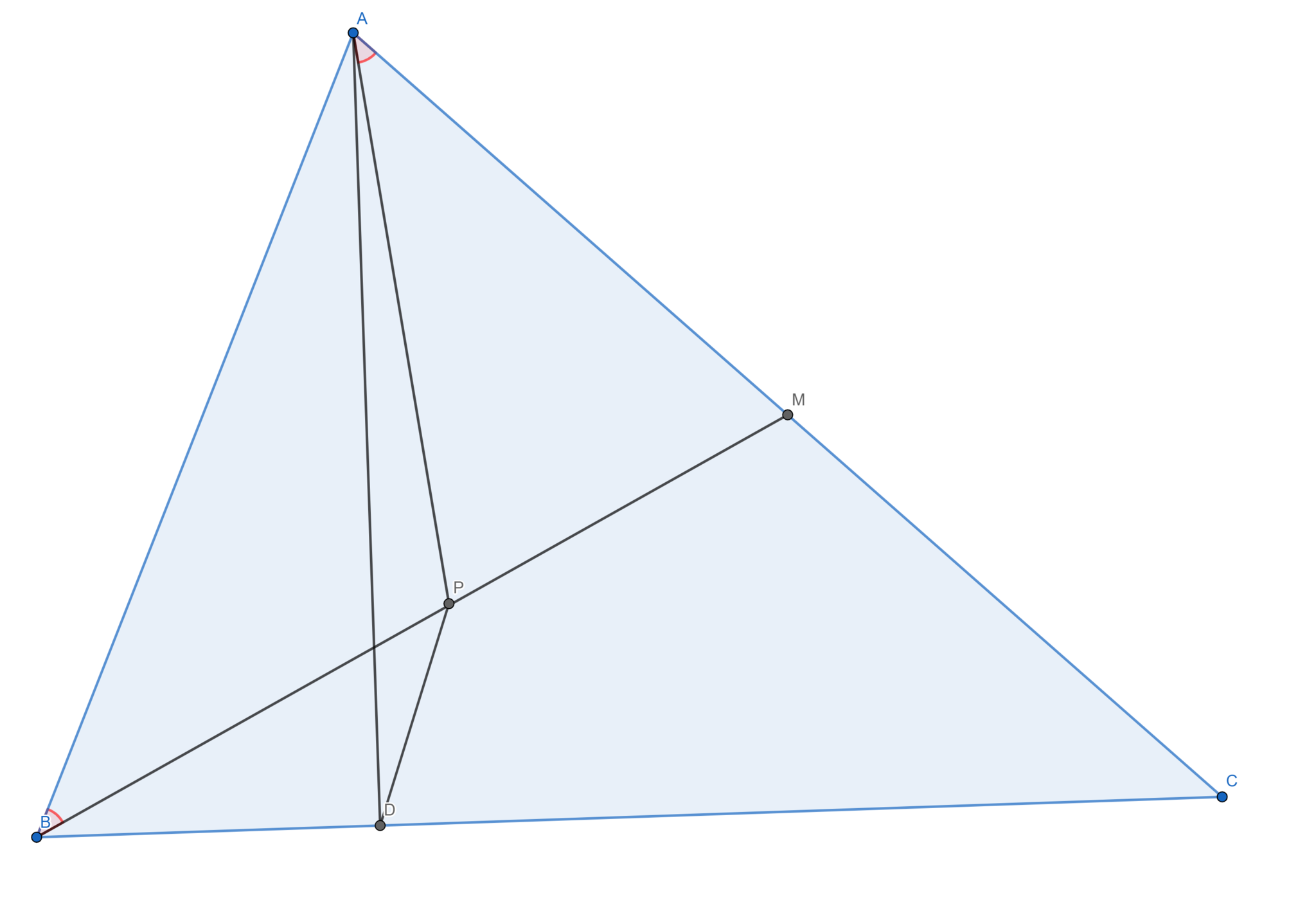 問題
問題
中点と直角があるので, $DM$結んで三角形$AMD$と$DMC$の二等辺ができるのは分かりますが, $\angle PDB = 115^\circ$の条件と結びつきませんね. 別のものを一旦探してみます.
条件から$MAP \sim MBA$は即座に分かります, そして$BM$を伸ばして平行四辺形作ってみたところ, 遠回りでしたが反対側で$MCP \sim MBC$が見つかりました.
実際のところ, これは$\frac{AM} {MP} = \frac{BM}{AM} \Leftrightarrow \frac{CM}{MP} = \frac{BM}{CM}$ から導かれます.
さて, なんとこれで既に必要なものは揃っています.
$\angle MDC = \angle MCD = \angle MPC$から, $4$点$M,C,D,P$は共円です.
よって $\angle PDB = \angle PMC$となり, 外角である$\angle PMA$は$65^\circ$となります.
以上より$\angle BAC = 78^\circ$が答えとなります.$\square$
余談
これだけで終わるのも味気ないので, $BM$伸ばしたときに見つけた, 同じ条件の求値で使えそうな性質の紹介をします.
$AP \cdot BC = CP\cdot AB$が成立.
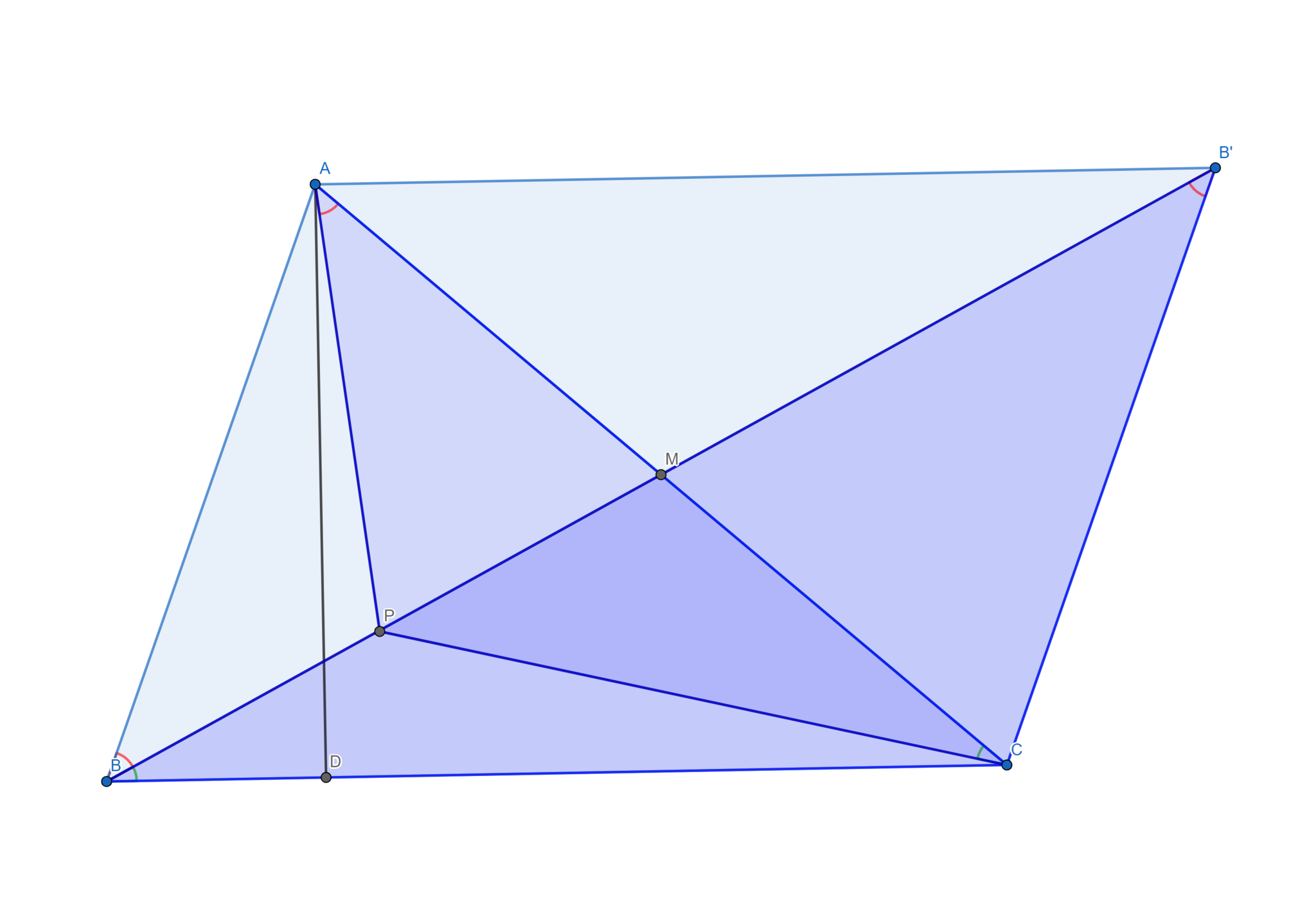 相似
相似
添付した図で$ACP \sim B'BC$となり, $\frac{AP}{CP} = \frac{B'C}{BC} = \frac{AB}{BC}$より成立.$\square$
以上です. 私は難角問題を解いた経験は殆どなかったため, 余計な考察をいろいろする羽目になりましたが, 解けた人には一瞬, 道が見えないと他の数え上げで体育会系するより時間のかかる, そんな問題だったと思います.
