角の二等分線の定理(証明)
はじめに
角の二等分線の定理について、正弦定理をつかって直ちに示されることに気づいたので
記録しておきます。
定理
図のように、三角形において、角の二等分線が対辺を分割する状況を考える。
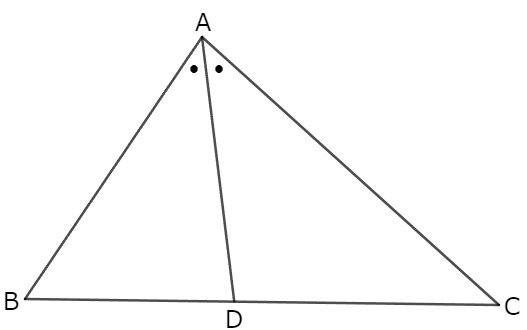
このとき、
$$\mathrm{BD}:\mathrm{DC}=\mathrm{AB}:\mathrm{AC}$$
が成り立つ
証明1
図のように角を$\alpha$,$\theta$とおく。
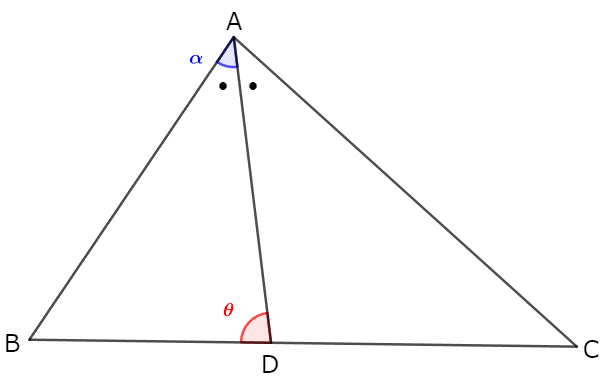
$\triangle \mathrm{ABD}$について正弦定理を考えると
$$\frac{\mathrm{BD}}{\sin \alpha}=\frac{\mathrm{AB}}{\sin\theta}$$
$\triangle \mathrm{ADC}$について正弦定理を考えると
$$\frac{\mathrm{DC}}{\sin \alpha}=\frac{\mathrm{AC}}{\sin\theta}\qquad\because \sin(\pi-\theta)=\sin \theta$$
辺々の比を取ると
$$\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}$$
したがって
$$\mathrm{BD}:\mathrm{DC}=\mathrm{AB}:\mathrm{AC}$$
証明2
点$\mathrm{D}$を通り辺$\mathrm{AC}$に平行な線を引くと下図のようになる。
$\angle \mathrm{ADE}=\angle \mathrm{DAC}$ ($\because$錯角)
$\angle \mathrm{EDB}=\angle \mathrm{ACB}$ ($\because$同位角)
$\mathrm{ED}=\mathrm{AE}$ ($\because$二角が等しいので$\triangle \mathrm{AED}$は二等辺三角形)
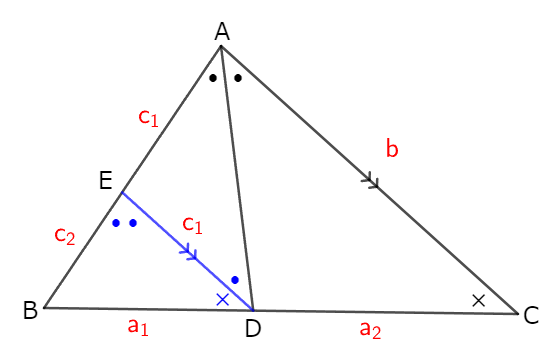
$\triangle \mathrm{ABC}$と$\triangle \mathrm{EBD}$は相似なので
$$(c_1+c_2+b):(a_1+a_2)=(c_2+c_1):a_1$$
よって
$$a_1(c_1+c_2+b)=(a_1+a_2)(c_2+c_1)$$
両辺で共通しているものを取り除くと
$$a_1b=a_2(c_1+c_2) $$
辺の表現を直すと
$$\mathrm{BD}\cdot \mathrm{AC}=\mathrm{DC}\cdot \mathrm{AB}$$
整理して
$$\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}$$
したがって
$$\mathrm{BD}:\mathrm{DC}=\mathrm{AB}:\mathrm{AC}$$