数学オリンピック2008本選解説 1~4 (JMO2008)

はじめに

こんにちは!!
今回は競技数学の典型問題が良い感じに詰まっていたJMO2008本選4を1セット解説します.残念ながら5はわからなかったので除外です.誰か教えてください.それではよろしくお願いします!

問題は こちら です.

解説

第一問

1番なのに主張がとても抽象的で結構難しそうですね.ですが,焦らずに落ち着いて解いていきましょう.僕は30分考えて進捗がなかったので2,3を考えてからまた45分くらい考えました.合計75分くらいで解きました.めちゃくちゃ沼ってますね.

①情報を式に落とし込む

まずは$P(x)$を文字で表さないと始まりません.ここで,整数係数多項式を以下のように表しましょう.$P(x)$は$m$次であるとします.

$$ P(x)=Q(x)(x-n^2) $$

さらに,$a$は有理数であるので$a=\frac{q}{p}$($p$,$q$は整数であり,互いに素)と置くことにしましょう.基本的には有理数であることよりも,$\frac{整数}{整数}$の形の方が扱いやすいです.

②式を処理する

さて,$P(a^2)$,すなわち$P(\frac{q^2}{p^2})$を考えてみましょう.

$$ P(\dfrac{q^2}{p^2})=Q(\frac{q^2}{p^2})(\frac{q^2}{p^2}-n^2) $$

となります.今回はこれが$1$でないことを示したいので背理法が刺さりそうですね.$P(\frac{q^2}{p^2})=1$と仮定します.

$$ Q(\frac{q^2}{p^2})(q^2-n^2p^2)=p^{2}　 \Longleftrightarrow q^2-n^2p^2=\frac{p^2}{Q(\frac{q^2}{p^2})} $$

少し扱いやすそうな式になりました.さらに$p^{2m-2}Q(\frac{q^2}{p^2})$は整数になるので,$q^2-n^2p^2=\dfrac{p^{2m}}{整数}$となります.さらに,左辺は整数であるから右辺の分母は$p^l$の形で表されます.

③仕上げ

$$ q^2-p^2n^2=p^{2m-l} $$

これほどまでに簡単な整数問題に帰着されました.左辺は$p$と$q$が互いに素なことより,$p$の倍数ではない整数となります.従って,右辺:$p^{2m-l}=p^0=1$となる必要があります.ここで,$q^2-p^2n^2=1$の整数解を考えます.$(q+pn)(q-pn)=1$となることになりますが,これは解なしです.よって,$n$が自然数である時矛盾が導かれました.

以上の議論から$P(a^2)=1$という仮定が間違っていたことになり$P(a^2)\not=1$を得ます.

第二問

こちらは方針が見えやすいオーソドックスな問題ですね.ある程度実験すれば見えてきます.僕は30分程度で解けました.

①実験をしてみる

あるプレイヤーが赤と白のカードを持っていた時に(r,w)などと表します.まずは各プレイヤーのカードがどのように変化していくのかを観察してみましょう.

(r,r)→(?,r), (r,w)→(?,w), (w,w)→(?,w)

このようになりますね.この遷移には特徴があります.それは(r,r)となるためには直前が少なくとも(r,r)である必要があるということです.つまり,(r,r)の人の数はターンが進むにつれて広義短調減少していくということです.(r,r)の人が0人になる状況はすなわち全員が(r,w)の状況なので目的の状況になります.なるほど,だいぶ本質的な性質を発見できましたね.

②ターンの最大数を上から評価するために

さて,出来るだけ長続きさせるためには(r,r)の人が一人でもいれば良いです.ということで,ある(r,r)の人に着目してその人を出来るだけ(r,r)の状態に保つことを考えてみましょう.そのためには(r,r)の人が次のターンにも(r,r)であるためにはどういった条件が必要なのかを考えるのが良いですね.(r,r)→(r,r)なので右隣のプレイヤーから$r$をもらう必要があります.つまり,右隣のプレイヤーは(r,r)か(r,w)となります.さて,帰納的に考えていけば(r,r)の人が$k$ターン後も(r,r)であるためにはその人から右隣$i$人の人が計$i$枚以上の赤いカードを所持している必要があります.($i$は$0$以上$k$以下の任意の正整数を動く.)

③ターンの最大数を上から評価する

　最初に(r,r)である人の中で最後まで(r,r)であるような人の一人に着目します.その人が$k$ターン後も(r,r)であるためにはその人から右隣$i$人の人が計$i$枚以上の赤いカードを所持している必要があります.ここで,赤いカードの残り枚数は$2006$枚なので最大で$2006$ターンは(r,r)を保つことができます.逆に$2007$ターン以上(r,r)に保つことはできないですね.よって(r,r)を保てる最大ターン数は$2006$以下です.逆にある人を(r,r),その左隣の人を(w,w),その他の人を(r,w)とすれば$2006$ターン(r,r)を保つことができます.よって,最大$2007$ターンで所望の状態にすることができるわけですね.

第三問

3番級にしては簡単な幾何ですね.個人的には1番でも違和感はないと思います.僕は大体45分くらいで解きました.

①図を描いてみる

まずは,図を書きましょう.大きくコンパスなどで正確に作図しながらです.

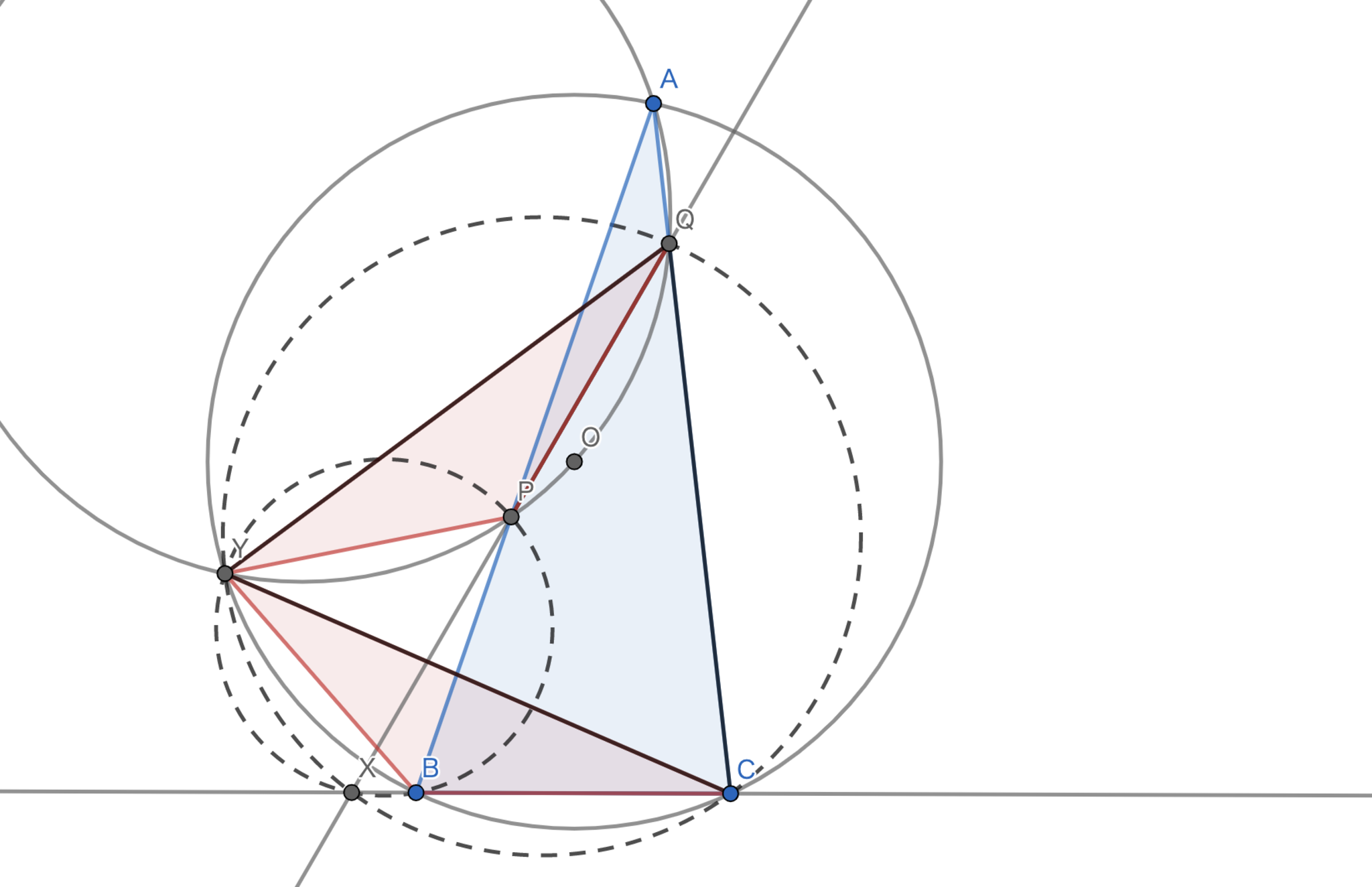JMO2008-3

こんな感じの図になりますね.今回は一般性を失わず$AB \ge AC$の図で考えます.さらに$X$を図のように$BC,PQ$の交点とします.ここで,$Y$も図のように定めます.(円の交点は情報が多いのでその点を利用したいという発想からです.)

②angle-chaseやlength-chaseで情報を増やす

情報を増やしていきましょう!共円がたくさんあるのでとりあえず,円周角の定理でたくさん情報を移していきましょう.
$\angle{BYC}=\angle{BAC}=\angle{PAQ}=\angle{PYQ}$,$\angle{BCY}=\angle{BAY}=\angle{PAY}=\angle{PQY}$の二点が得られます.このことから,$\triangle{YPQ} \backsim \triangle{YBC}$であることがわかります.このことの何が嬉しいかというと,$PQ=BC$という条件が刺さりそうなことです.$PQ=BC$なので$\triangle{YPQ}\equiv \triangle{YBC}$であるとわかります.合同は情報の宝庫です.例えば,$YQ=YC$であることがわかります.角度の問題において,二等辺三角形は強力ですからありがたいですね.

③角度を文字で置いてさらに追ってみる

二等辺三角形が出てきたのでその底角を文字で置いてみましょう.$\angle{YBC}=\alpha$とおきます.すると二等辺三角形なので$\angle{YQC}=\alpha$ですね.まだ,Oが外心であることを利用してないですから,利用しましょう.中心角の定理より$\angle{YOA}=2\angle{YCA}=q\angle{YCQ}=2\alpha$となります.また,共円より$\angle{YOA}=\angle{YQA}$なので$\angle{YQA}=2\alpha$となります.$\angle{YQA}+\angle{YQC}=3\alpha=180°$なので$\alpha=60°$となります.

④仕上げ

一つ角度が出てしまえばこっちのもんです.まずは$\triangle{YCQ}$が正三角形であることがわかります.また,$\angle{YQX}=\angle{YCX}$であるから$Y,Q,C,X$は共円です.従って,$\angle{QXC}=\angle{QYC}=60°$となります.ということで,答えは$60°$です.

第四問

FEは4番級以降はどれもかなり難しい印象があります.この問題は個々のステップの難易度は低いですが,ステップ数がかなり多いので総合的に難しい問題でした.僕もかなり苦戦しました.

①解の予想

まずは解の予想です.これは非常に重要なステップです.ここを間違えると結構沼にハマってしまったりするので慎重に予想しましょう.まずは明らかに$f(x)=x$はokそうだなと予想ができます.では$f(x)=cx$や$f(x)=x+k$などはどうでしょうか?これらを実際に試してみるとダメそうだなとわかります.二次式はどうでしょう?こちらも無理そうですね.最後に定数関数です.$f(x)=0$なんかは容易に満たすことがわかりますね.

ということで,暫定的には$f(x)=x,f(x)=0$の二つが解であると予測してみましょう.

②代入しまくる

$P(a,b)$で$(x,y)$に$(a,b)$を代入することを表すものとします.（以下では解答に一直線に正しい代入を次々としていますが,もちろんそんなことは現実的には不可能です.色々な代入をして試行錯誤して発見していきましょう.）

$P(0,0)$より$f(0)f(f(0))=0$を得ます.この式はあまり役立たないように見えるかもしれませんが,さらにシンプルな情報に変換することができます.ここでは$f(0)$か$f(f(0))$のどちらかが整数であるので場合わけをしましょう.$f(0)=0$の時,$f(f(0))=f(0)=0$となります.$f(f(0))=0$の時はそのまま$f(f(0))=0$です.つまりどちらのケースにおいても$f(f(0))=0$となる訳です.

$P(0,x)$より,$f(x)f(f(0)-x)=-xf(x) \ \forall_x \in \mathbb{R}$を得ます.これと似た形を$f(f(0))=0$を使えば作れそうなので次のようなことを考えます.

$P(f(0),-x)$より,$f(f(0)-x)f(f(f(0))+x)=f(0)f(f(0))+xf(-x)$すなわち$f(x)f(f(0)-x)=xf(-x)　\ \forall_x \in \mathbb{R}$を得ます.

従って,任意の実数$x$に対して$xf(x)=-xf(-x) ... ①$です.これは嬉しいですね.もう少し代入して式を集めてみましょう.

$P(x,-x)$より,$f(0)f(f(x)+x)=xf(x)+xf(-x) \ \forall_x \in \mathbb{R}$を得ます.
$P(x,f(x))$より,$f(0)f(f(x)+x)=xf(x)-f(x)f(f(x)) \ \forall_x \in \mathbb{R}$を得ます.
これらを比較して$xf(-x)=-f(x)f(f(x)) \ \forall_x \in \mathbb{R} ... ②$を得ます.

①や②から$x\not=0$かつ$f(x)\not=0$だったりすると割れたりして嬉しそうです.(ゼロで割ることはできないので気をつける必要があります.)

では,もし$x\not=0$かつ$f(x)\not=0$だとどんな嬉しいことがあるでしょうか?①から$-f(x)=f(-x)$を得ます.これは奇関数の性質ですね.さらに,$f(x)=f(x')$となる$x'$を取ります.②より$xf(x)=-f(f(x))f(x)=-f(f(x'))f(x')=x'f(x')$となって,$x=x'$となります.すなわち$f(x)=f(x')$ならば$x=x'$となる訳です.

③議論を進める

とりあえず,$f(x)=0$が解となっていることはわかるのでここで大事なのはそれ以外の解が存在するかどうかですから,$f(x)\not=0$なる$x$が存在するとしても良いですね.ここで,ゼロ除算の都合で$f(x)\not=0$なる$x$が$0$のみである場合とそうでない場合で場合分けして考えましょう.

case1:$f(x)\not=0$なる$x$が$0$のみである場合

この時,$f(x)= \begin{eqnarray} \left\{ \begin{array}{l} 0 \ (x \not=0) \\ c \ (x=0) \end{array} \right. \end{eqnarray}$($c$は任意の実数.)となります.これは与式を満たすので解の一つです.

case2:$f(x)\not=0$なる$0$でない$x$が存在する場合

$k$を$f(k)\not=0$なる実数とします.この時,$P(0,x)$と奇関数の性質より$k=f(k-f(0))$となり,②より$k=f(f(k))$であるから$f(f(k))=f(k-f(0))$となります.さらに,$f(x)=f(x')$ならば$x=x'$なので$f(k)=k-f(0)$となります.$f(f(k))=f(k-f(0))$となります.ここで,$f(k-f(0))\not=0$で$k-f(0)\not=0$ならば$f(k-f(0))=k-2f(0)=k$となり$f(0)=0$を得ます.$f(k-f(0))=k$なので一つ目はクリアです.だからなんとかしてそれらを証明したいですね.二つ目は$k\not=f(0)$であることを示せればよさそうです.背理法を使いましょう.$f(k)=0$と仮定します.すると,$f(k)=f(f(0))=0$となってしまうので矛盾します.従って,$f(k)\not=0$です.よって,$x,f(x)$が共に$0$でないならば$f(x)=x$となります.

今度は$f(l)=0$なる実数$l$を考えてみます.$|k|\not=|l|$であることに注意しましょう.$P(k,l):f(k+l)f(k-l)=k^2$を得ます.このことから,$f(k+l),f(k-l)$は共に$0$でないことがわかります.$x,f(x)$が共に$0$でないならば$f(x)=x$となるので$f(k+l)f(k-l)=k^2-l^2=k^2$となり$l=0$を得ます.すなわち,$f(l)=0$ならば$l=0$となるわけです.

よって,$f(0)=0$であり,$0$でない任意の実数$x$に対して$f(x)=x$であるとわかります.これらを併せて$f(x)=x \ \forall_x\in \mathbb{R}$となる訳です.

④結論(十分性の確認も含めて)

以上より,$f(x)=x,f(x)= \begin{eqnarray} \left\{ \begin{array}{l} 0 \ (x \not=0) \\ c \ (x=0) \end{array} \right. \end{eqnarray}$($c$は任意の実数.)の二つが解となります.これらがちゃんと与式を満たしていることも確認しておきましょう.

総括

この年はとても解きやすい年だったと思います.EGMO一次レベルの問題が解けるようになってきた人はJMOの2004~2008あたりをまず解くと良いと思います.ここら辺は良問がかなり多いです.個人的にはJMO2007-1,JMO2007-3,JMO2004-2,JMO2007-4あたりがかなりオススメです.

この年の平均点は高そうですが,1,2,4の記述を全て完璧にするのはかなり難しいと思います.

個人的な難易度の順番:3<2<1<4
例年の$n$番級との難易度の比較(左から順に$n=1,2,3,4$):標準やや難,易標準,易,標準