初等幾何の観点から「軌跡と領域」を嗜む
はじめに
『初等幾何の観点から「軌跡と領域」を嗜む』などと大層なタイトルを掲げてしまいましたが,要するに初等幾何的な別解を考えようという記事です.元の解法よりも遠回りなものもあるかもしれませんが,面白いのでよかったらみていって下さい!それではよろしくお願いします.
軌跡と領域を初等幾何でねじ伏せよう
アポロニウスの円
平面上に二点$A,B$をとる.$A,B$からの距離の比がそれぞれ$1:2$であるような点の軌跡を求めよ.
まずは,ウォーミングアップに定番の初等幾何的解法を紹介していきます.
直線$AB$を$1:2$に内分する点を$C$,外分する点を$D$とする.この時,$P$を$PA:PB=1:2$を満たすような点とします.すると$PA:PB=CA:CB, \ PA:PB=AB:AD$となるので角の二等分線となるわけです.よって,$PA:PB=1:2$が成り立っているならば必然的に$\angle{CPD}=90°$であるから$P$は$CD$を直径とする円上にあるというわけです.(逆は簡単に確認できます.)
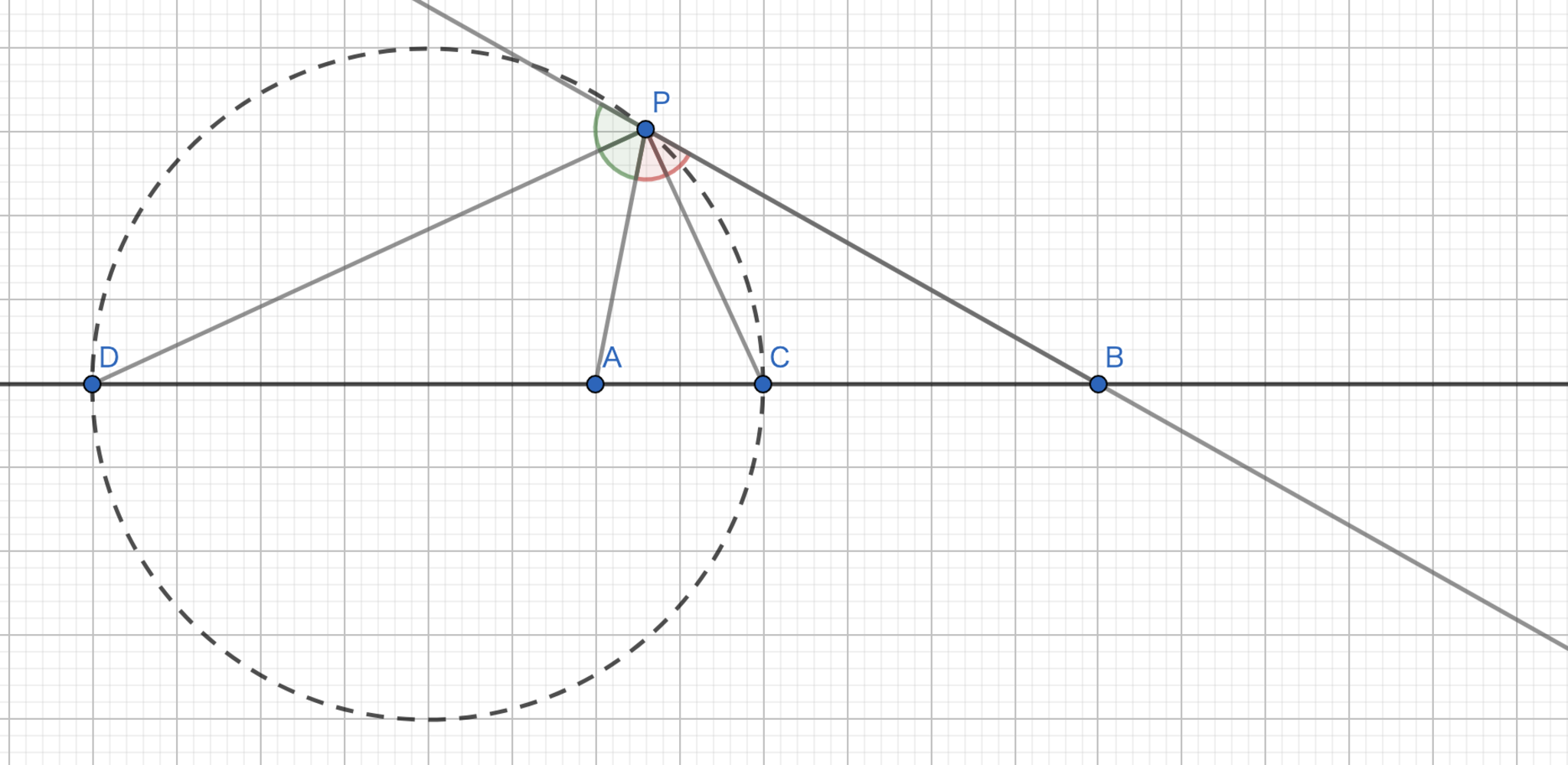 アポロニウスの円めっちゃ好き
アポロニウスの円めっちゃ好き
相似拡大
$A(-2,0)と$単位円$c$:$x^2+y^2=1$上に点$P$をとる.$P$が$c$上を動く時,$AP$の中点$M$の軌跡を求めよ.
$M$は$A$を中心に$B$を$\frac{1}{2}$倍に拡大した点であるから,その軌跡は$c$を$A$を中心に$\frac{1}{2}$倍に拡大したものとなります.よって,$(x+1)^2+y^2=(\frac{1}{2})^2$が求める軌跡です.
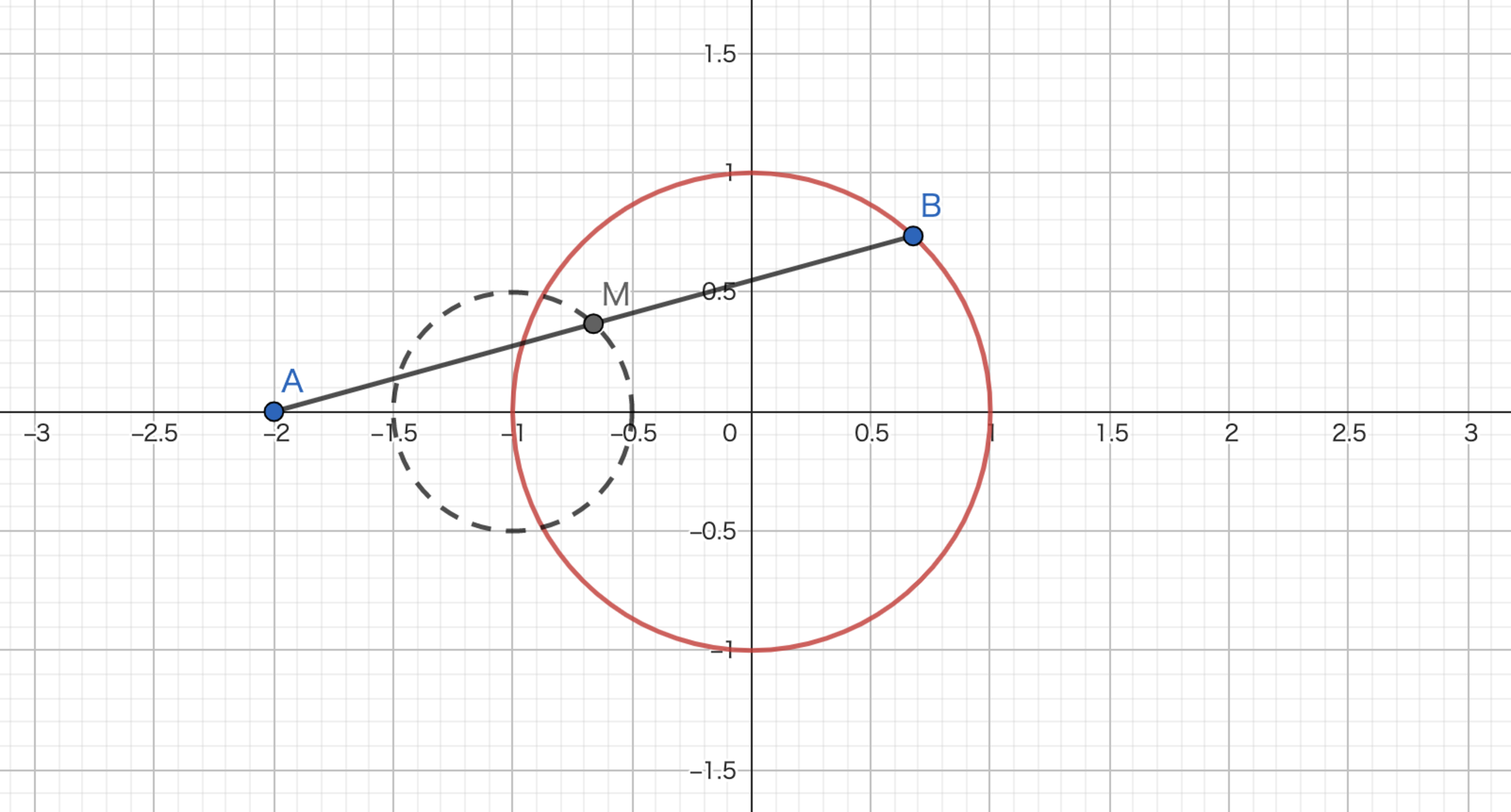 相似拡大いっぱいちゅき
相似拡大いっぱいちゅき
円
$A(1,0)$とし,$y=kx$に関して$A$と対称な点を$P$とする.$k$が任意の実数をとるとき,$P$の軌跡を求めよ.
対称移動した点であるから$OA=OP=1$が常に成り立つので$P$は$O$を中心とする半径$1$の円$\Gamma$上にあることがわかります.よって,軌跡は$\Gamma$の一部(もしくは全部)であることがわかります.逆に,$\Gamma$上$(-1,0)$以外の任意の点においては題意を満たす$k$が存在するので求める奇跡は$\Gamma$の$(-1,0)$以外の部分になります.
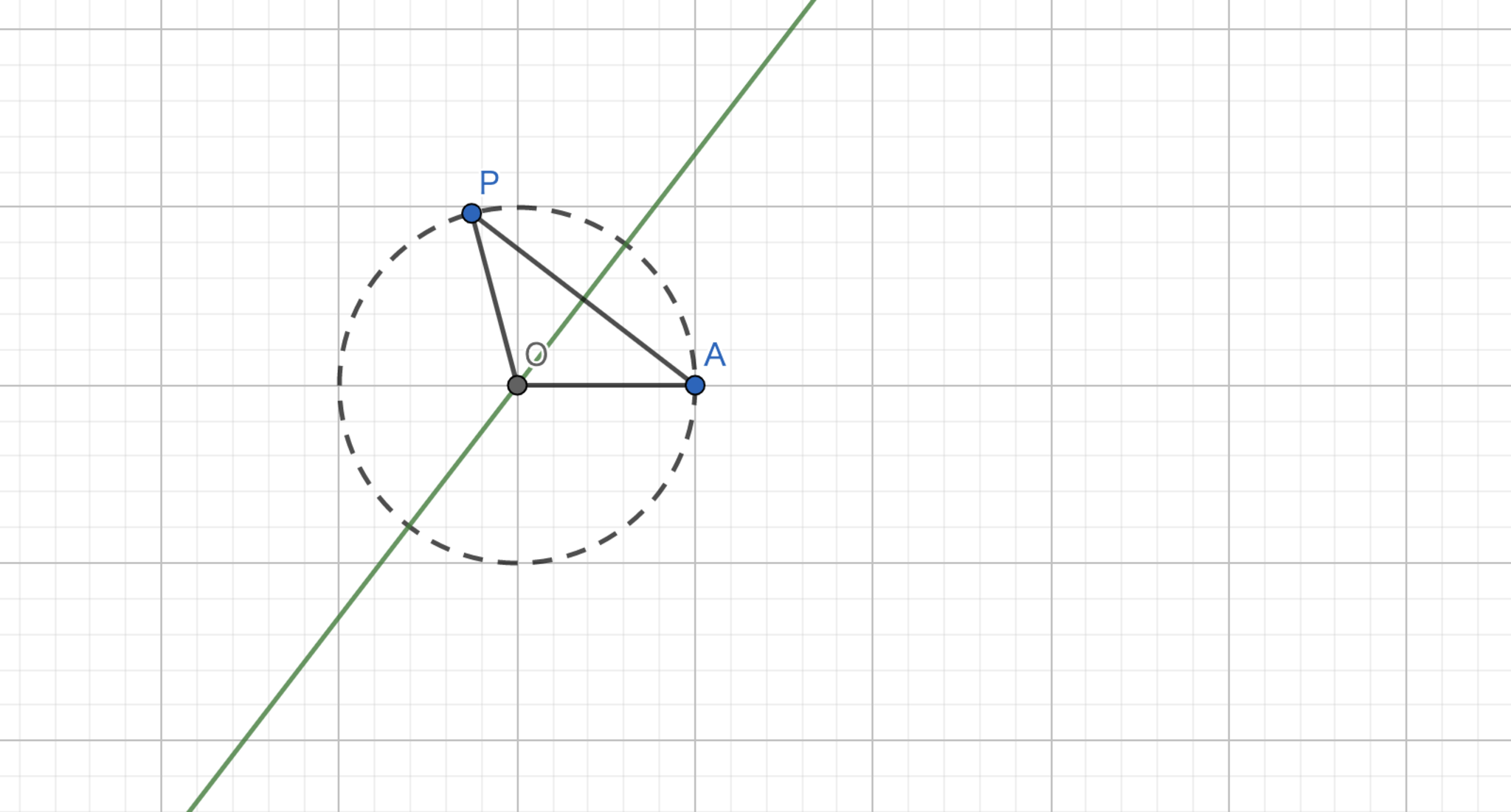 定義から円を考える
定義から円を考える
放物線+相似
放物線:$y=ax^2$の準線の式を求めよ.
全ての放物線は相似なのです!
ポイント:任意の放物線は相似の関係にあるので$y=x^2$の場合についてのみ考える
まずは,$P(1,1)$における接線を考えます.微分して,$y=2x-1$を得ます.これの法線を考えると$y=-\frac{1}{2}x+\frac{3}{2}$を得ます.ここで,焦点を$Q(0,q)$,法線に関して$Q$と対称な点を$R$とし,$P$に関して$R$と対称な点を$R'$とします.
このとき,$PQ=PR=PR'$であるので$\angle{RQR'}=90°$を得ます.また,法線と$QR$は直行するので$QR'$と法線は平行となります.よって,$QR'$の式は$y=-\frac{1}{2}x+q$であることがわかります.あとは,この直線を通る点が一つ分かれば$q$の値が定まります.
$H$を$R'$から$x$軸へ下ろした垂線の足とし,$S$を$OH,QR'$の交点とします.この時,$\angle{QSO}=\angle{R'SH},QO=R'H,\angle{QOS}=\angle{R'HS}=90°$となるので$\triangle{QSO} \equiv \triangle{R'SH}$を得ます.よって,$S$は$OH$の中点となるわけですね.以上より,$QR'$は$S(\frac{1}{2},0)$を通るので$q=\frac{1}{4}$を得ます.よって準線の式は$y=-\frac{1}{4}$となります.
$y=x^2$と$y=ax^2$の相似比は$1:\frac{1}{a}$であるので一般に$y=ax^2$の準線の式は$y=-\frac{1}{4a}$となります.
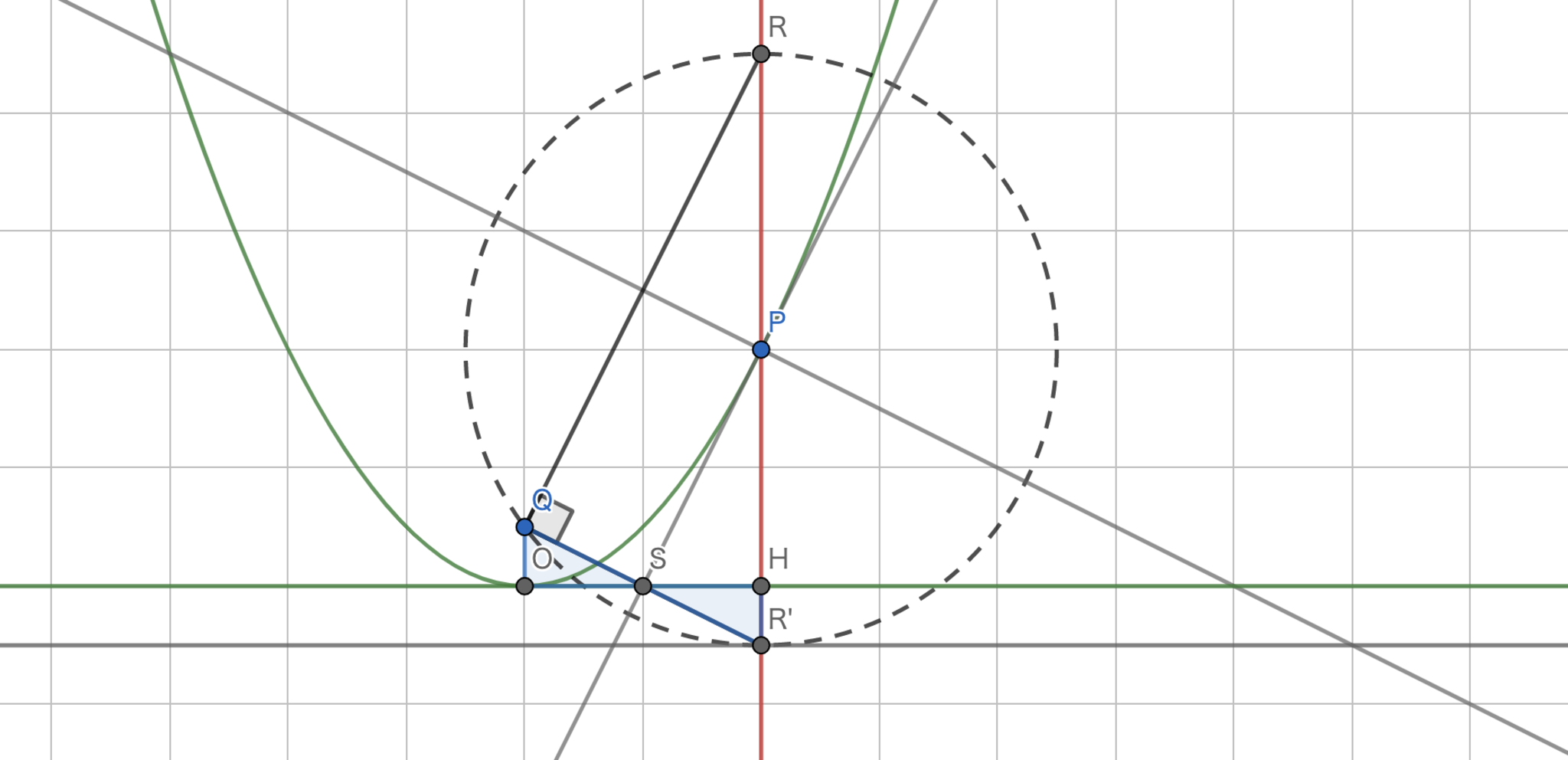 放物線を幾何的に見るの最高に楽しい
放物線を幾何的に見るの最高に楽しい
放物線+相似2
放物線$y=x^2$上に相異なる二点$A,B$をとった時,それらの接線が点$C$で直交した.$C$の軌跡を求めよ.
これも気持ちよく初等幾何的に解けます!
焦点を$P(0,q)$,準線を$y=-q$とし,$A,B$から準線へと下ろした垂線の足を$X,Y$とします.問題2でやった通り,$AC \perp PX, BC \perp PY$を得ます.よって,四角形$PDCE$は長方形となります.また,定義より$AP=AX, BP=BY$であるので$D,E$はそれぞれ$PX,PY$の中点となります.すなわち,$D,E$は$x$軸上に位置することになります.よって問題を以下のように言い換えることができます.
$P$を固定した長方形$PDCE$は$D,E$を$x$軸上に持つ.このとき,$C$の軌跡を求めよ.
長方形の対角線がそれぞれ中点で交わることより,求める$C$の軌跡は準線となります.
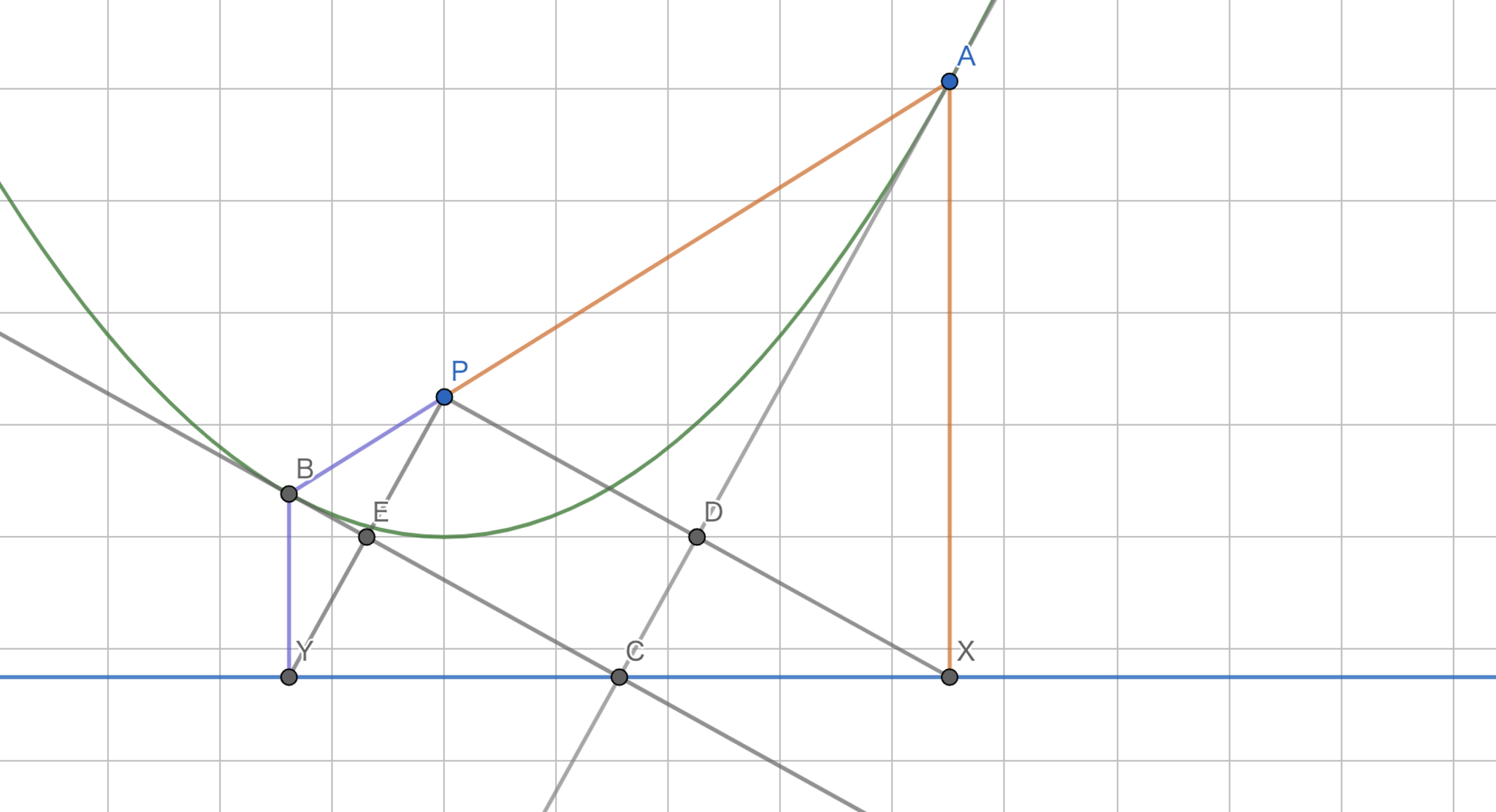 放物線気持ちいいいいい!
放物線気持ちいいいいい!
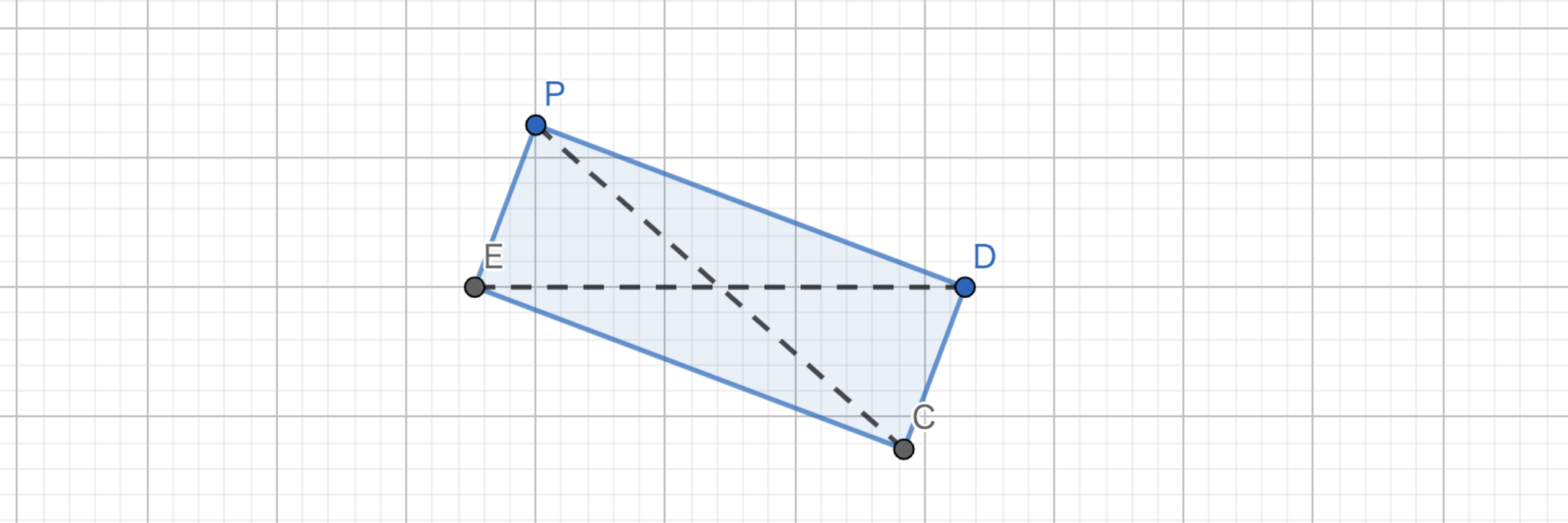 長方形!
長方形!
方べきの定理
単位円$c$:$x^2+y^2=1$上の点$P$をとり,定点$A(-2,0)$から$P$へ線分を引き,その線分の$P$の側の延長線上に点$Q$を$AP\cdot PQ=3$となるようにとる.$P$が$C$上を動くとき,$Q$の軌跡を求めよ.
まずは,方べきの定理で長さの情報を出していきます.$AR \cdot AP=AB \cdot AC =3$を得ます.一方で$AP \cdot PQ =3$であることから$AR=PQ$を得ます.つまり,$QP \cdot QR = 3$であるので方べきの定理を再び適用することにより$QO=2$を得ます.
上の議論から,常に$OQ=2$が成り立っていることがわかります.よって,$Q$の軌跡は$O$を中心とする半径$2$の円$\Gamma$の一部(あるいは全部)ということになります.$Q$は直線$AP$上にあることから,直線$AP$が取りうる範囲内かつ$\Gamma$上である必要があります.逆にそのような範囲内では題意を満たすことが容易にわかります.よって答えは$\Gamma$上の$x$座標が$1$以上の部分となります.
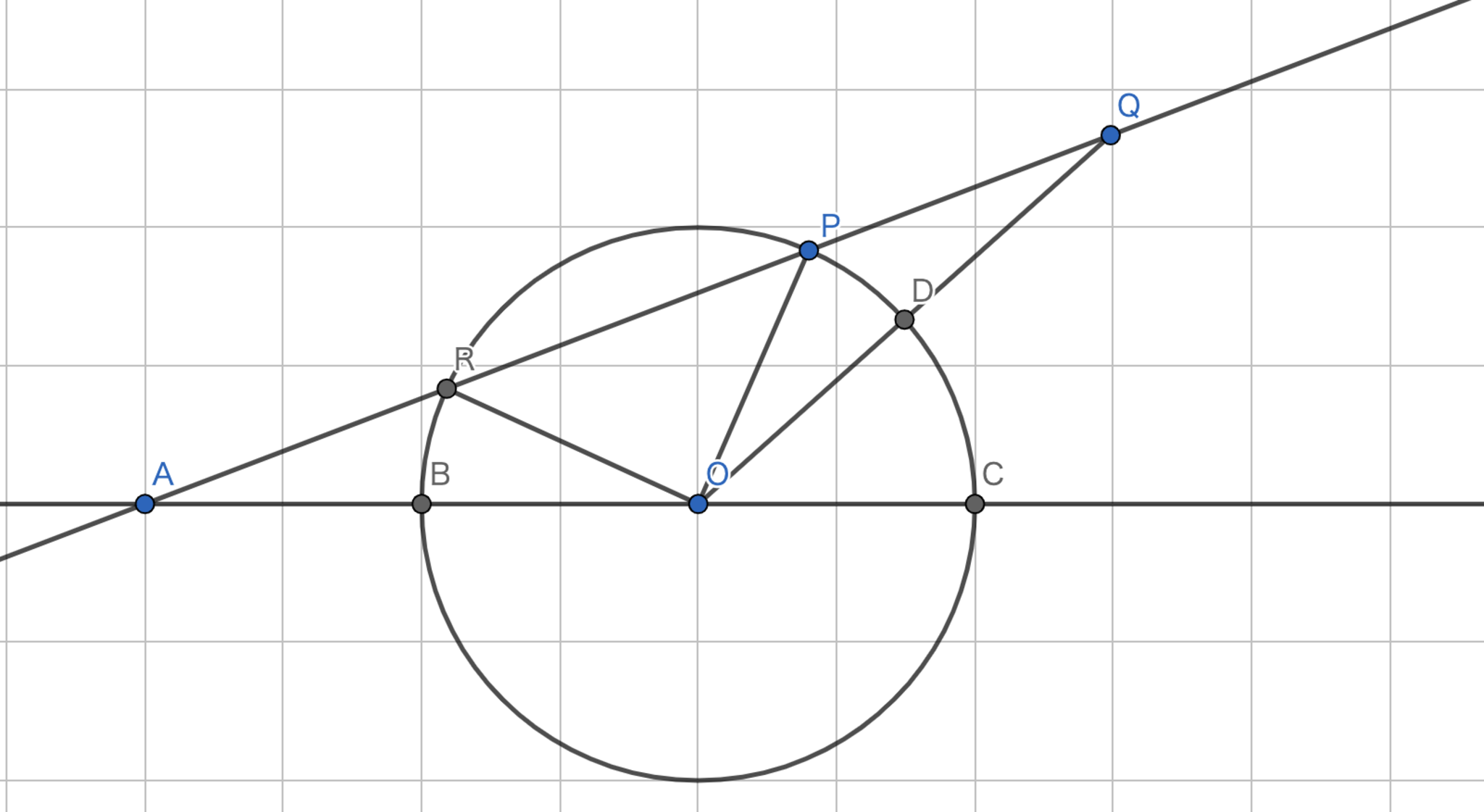 方べきの定理!!
方べきの定理!!
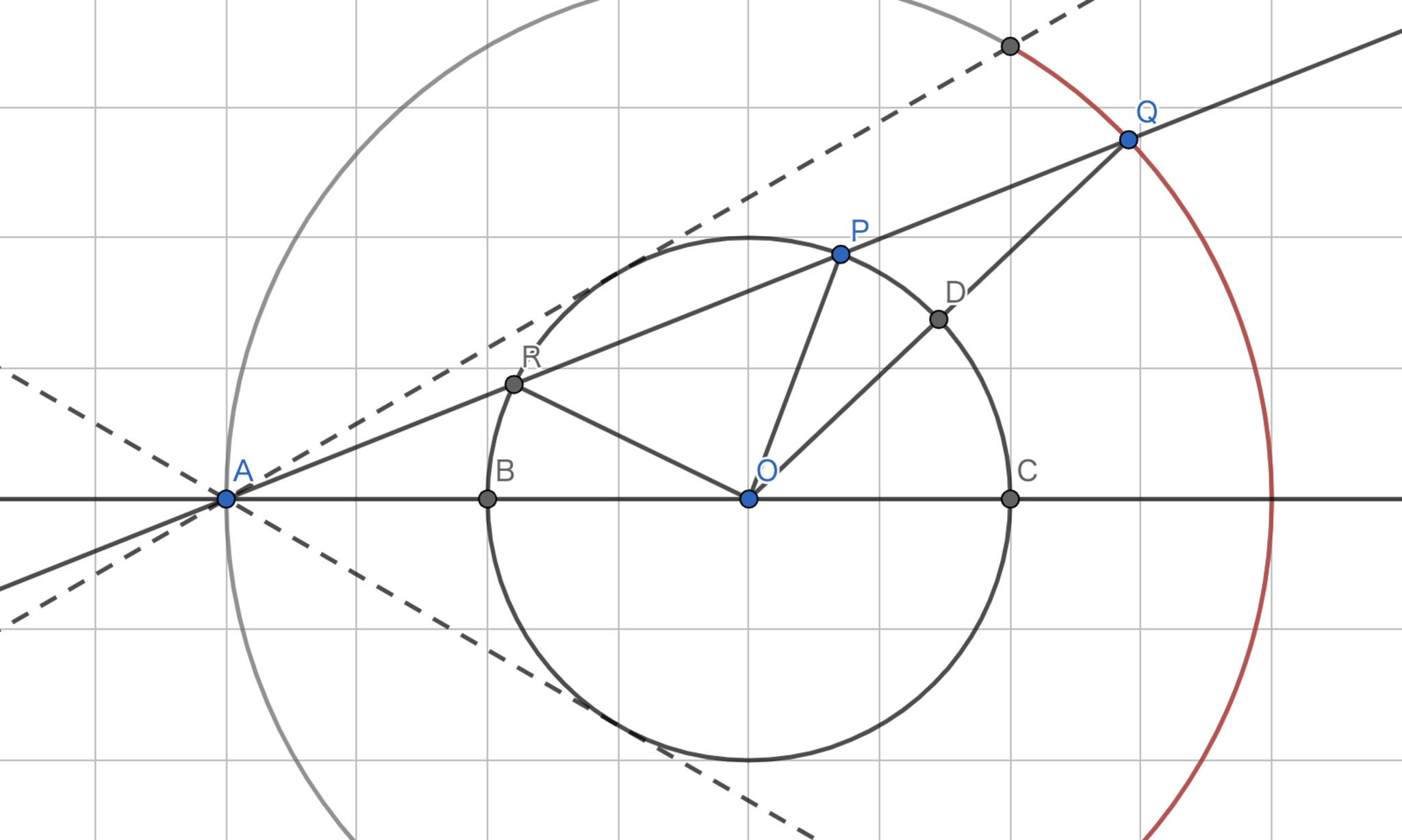 接線で挟もう!!!
接線で挟もう!!!
円周角の定理+平面の場合分け
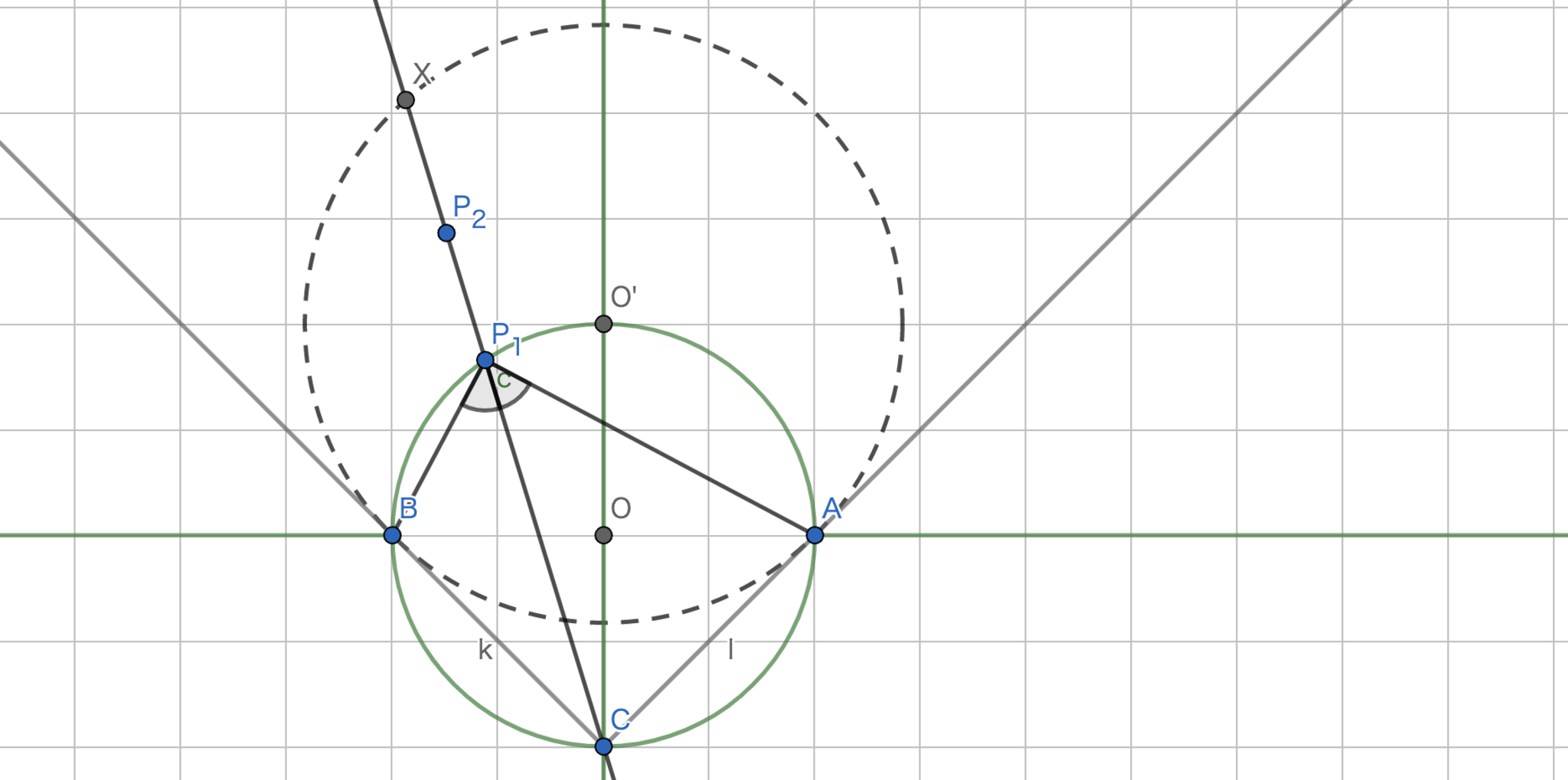
座標平面上の三点$A(1,0),B(-1,0),C(0,-1)$に対し,$\angle{APC}=\angle{BPC}$をみたす点$P$の軌跡を求めよ.ただし,$P\not=A,B,C$とする.
これは座標で解くのはちょっと重そうな問題ですよね.ちなみに,こういった構図がシンプルな奇跡と領域の問題は大抵初等幾何で解けます.
まず,この図を見たときに図のように点$X,P$を取れば$XP$が三角形$XAB$の$X-Symmedian$となり,Symmedianの構図なので,角の二等分線が登場しそうだなと発想することができます.よって,$\triangle{ABC}$の外接円をメインに議論を進めていきましょう.(Symmedianが背景にあることを強調したいのでこのように書きましたが,円周角の定理に気づくことでも発想できます.)
$\triangle{ABC}$の外接円を$\Gamma$とします.ここで,$y$軸上の点,$x$軸上の点のうち線分$AB$でないものは明らかに解であるので以下では除外して考えていきます.
$ $
case1.$y>0$,$x\not=0$かつ$\Gamma$上の点$P_1$
まずは$y>0$,$x\not=0$かつ$\Gamma$上の点$P_1$を考えます.これは円周角の定理より題意を満たします.
$ $
case2.$CP_1$上の$P_1$でない点$P_2$
$P_1$はcase1で定めたものとします.$CP_1$上の$P_1$でない点$P_2$を考えます.ここで,$\angle{P_1P_2A}=\angle{P_1P_2B}$と仮定します.すると,$\angle{P_1P_2A}=\angle{P_1P_2B}$と併せて$\triangle{P_1P_2A} \backsim \triangle{P_1P_2B}$を得ます.すなわち,$\frac{P_1A}{P_1P_2}=\frac{P_1B}{P_1P_2}$であるから,$P_1A=P_1B$を得ます.これは仮定に矛盾するので$CP_1$上の$P_1$でない点は題意を満たしません.
$ $
case3.直線$CA$に関して$O$を含まない側かつ直線$CB$に関して$O$を含む側にある点$P_3$
このとき,$\angle{BP_3C}=\angle{BP_3A}+\angle{CP_3A}$となるので不適です.
$ $
case4.直線$CB$に関して$O$を含まない側かつ直線$CA$に関して$O$を含む側にある点$P_4$
case3と同様.
$ $
 Symmedianの知識から攻略のヒントが見える!!
Symmedianの知識から攻略のヒントが見える!!
正三角形を作る+相似変換
問題8を@aburi_roll_cakeさんから教えていただきました.ありがとうございます!
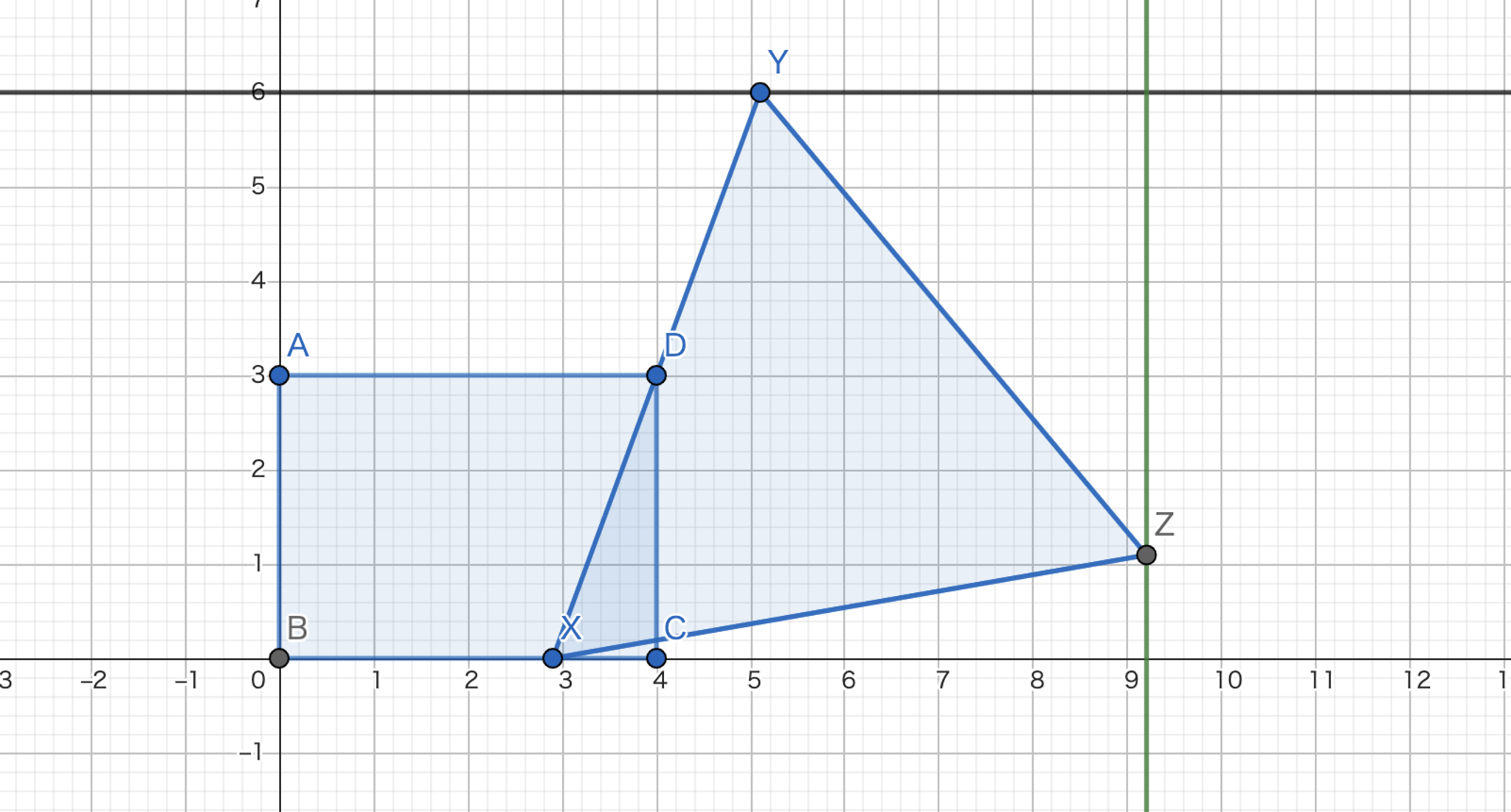
長方形$ABCD$は$AB=3,BC=4$を満たす.点$P$が頂点$B$から出発して以下の条件を満たしながら移動するとき,頂点$D$へ到達する時間が最短の経路を求めよ.
条件:辺$AB,BC$上では速さ$2$で移動し,それ以外では速さ$1$で移動する.
微分したくなるけど,これが回避できるらしい!すごすぎ!!この問題は辺の上をいい塩梅で伝って効率よく反対の頂点へ行く方法は?ということを聞いているのですね.
「辺を伝う」→「$D$へと直進する」の流れ(どちらかのステップがない場合もある)が最短経路であることがわかります.まず,$BC$を伝っていく方法を考えてみましょう.辺$BC$上の点$X$で方向転換するとします.$BX+2XD$の長さの最小値を計算すれば良いことになります.$2DX$という長さは初等的に扱いづらいので,$X$を$D$に関して対称移動させた点を$Y$として$BX+XY$の長さを計算することにします.$X$が$x$軸上を動く時,$Y$がなす軌跡は$y=6$となります.ここで,$XY$が扱いにくいので正三角形を作って情報を移してみます.$BX+XY=BX+XZ$なので$BX+XZ$を最小化すれば良いことがわかります.$Z$がなす軌跡が知りたいので$Y$と$Z$の関係を見てみましょう.$Z$は$Y$を$D$を中心に時計回りに$90°$回転させて$\sqrt{3}$倍に相似拡大した点となります.よって,$Y$の軌跡が$y=6$なので$x$の軌跡は$x=4+3\sqrt{3}$となります.問題を簡略化することができましたね!
$B$から直線$x=4+3\sqrt{3}$への最短距離は$4+3\sqrt{3}$となり,それは$x(4-\sqrt{3},0)$の時に実現できるのでこの場合の最短時間経路の長さは$4+\sqrt{3}$となります.いやぁ,すごいですね.
 これを、こうじゃ。
これを、こうじゃ。
正三角形+相似変換+平面の場合分け
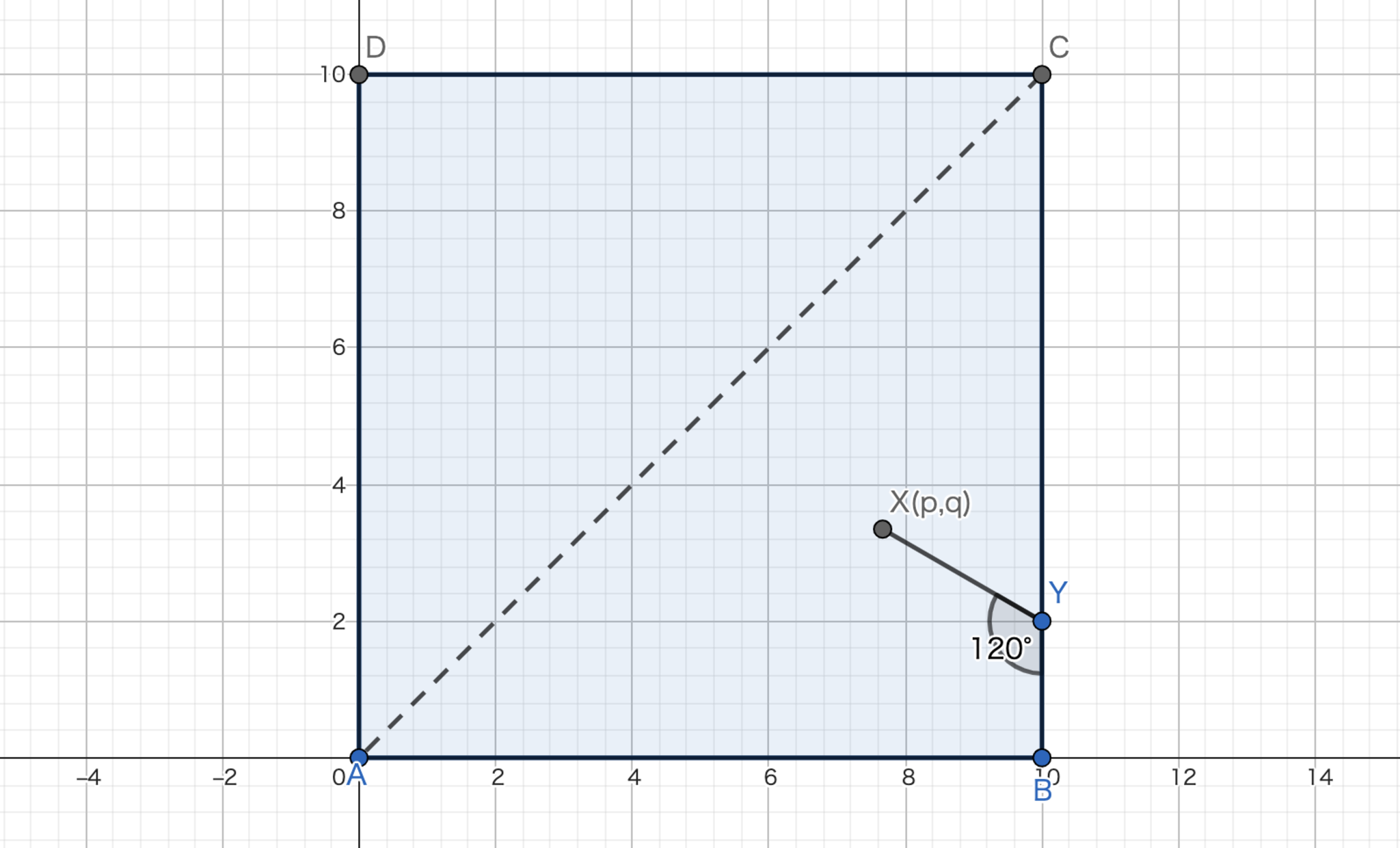
いっぺんの長さが$10$mの正方形のプールの一つの角に監視員を置く.この監視員は水中は秒速$1$m,プールの縁上は秒速$2$mで移動するとする.この監視員がプールのどこへでも到達しうるには最短で何秒必要か計算せよ.ただし,物事を単純化するため監視員は点,プールの縁は線と考え,監視員はプールを自由に方向転換して泳げるものとする.
東工大で類似の問題が出題されているのを発見しました.基本的な問題ですので頑張りましょう!僕が調べた範囲では初等幾何的解法は見つかりませんでした.どれも微分で解いていましたが,微分は回避できます!!
$ $
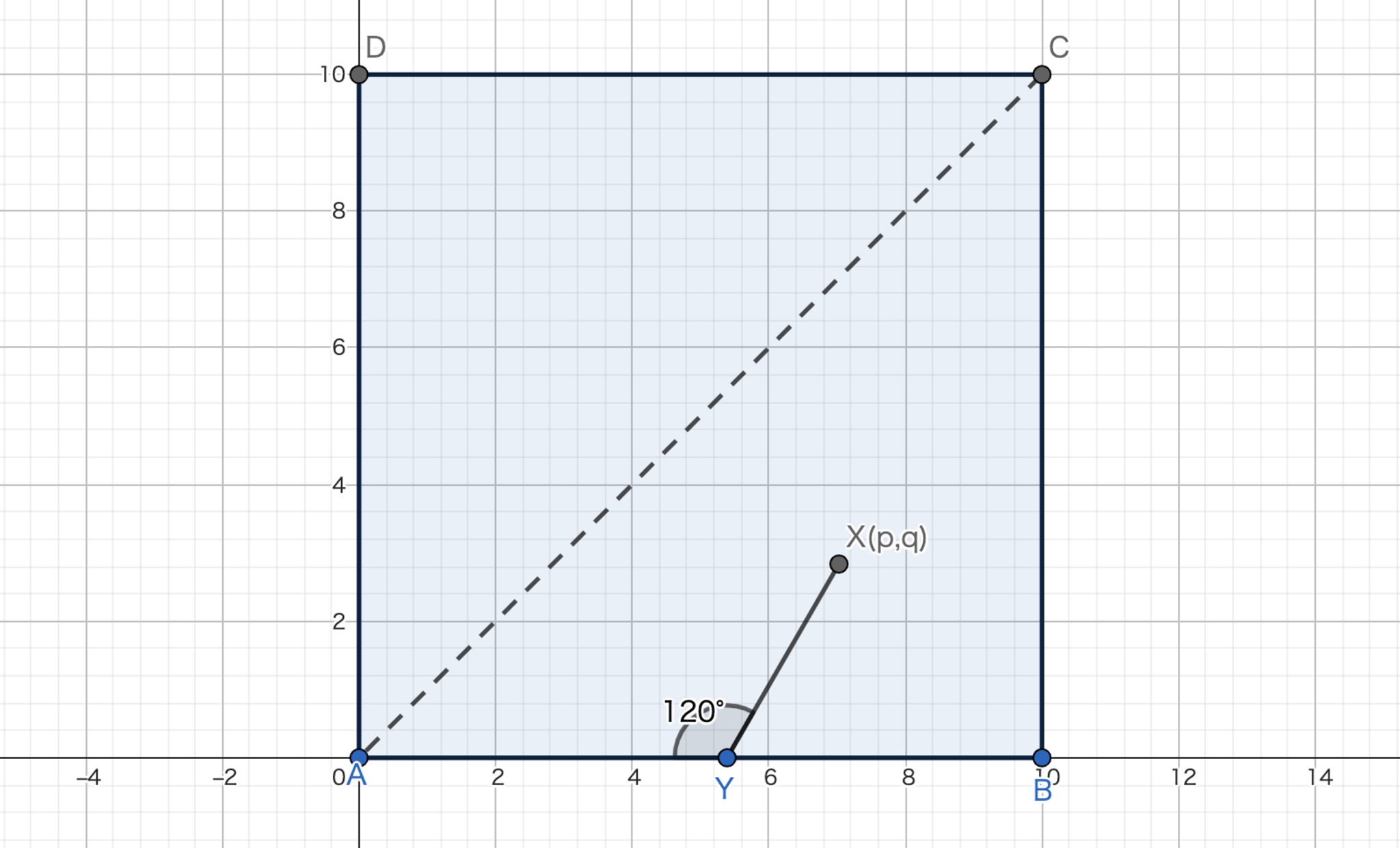
まず,以下のように図を定めます.このとき,$x$負方向と,$y$負方向に進むことはないとして良いですね.さらに図のには対称性があるので右下半分だけを考えれば十分であることがわかります(周を含む$\triangle{ABC}$のこと).
case1.辺$AB$を伝うが辺$BC$は伝わない場合
さて,まずは辺$AB$を伝うが辺$BC$は伝わない場合を考えてみましょう.この場合は問題8より,ある点$X(p,q)$へ行くには$\angle{AYX}=120°$を満たす辺$AB$上の点$Y$まで縁を進み,そこから方向転換すれば良いですね.そこまでにかかる時間は$\frac{1}{2}\left(p-\frac{q}{\sqrt{3}}\right)+\frac{2q}{\sqrt{3}}=\frac{p}{2}+\frac{\sqrt{3}q}{2}$秒となりますね.
 プールです。
プールです。
case2.辺$AB$と$BC$を共に伝う場合
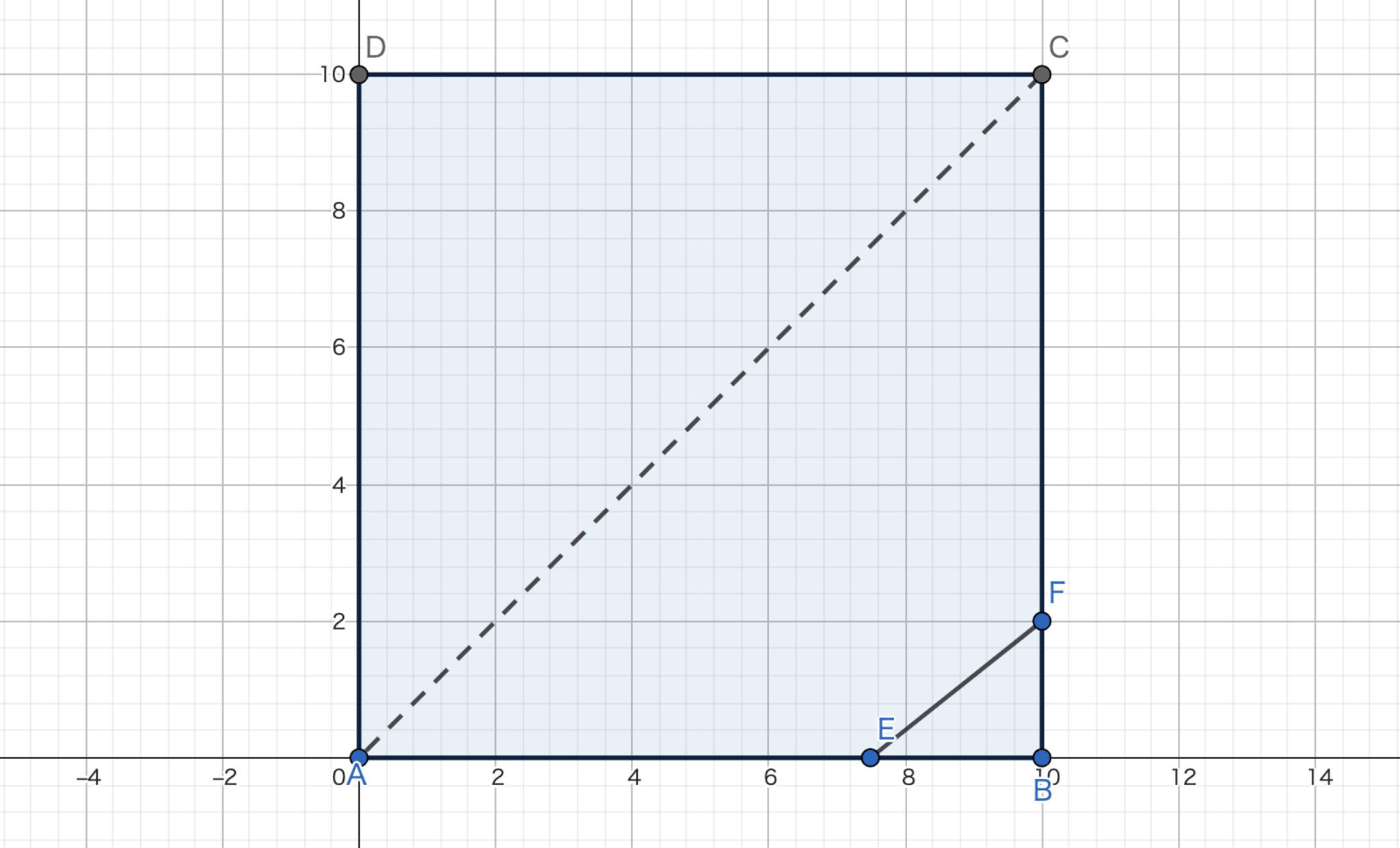
次に,辺$AB$から辺$BC$を伝ってから$X$へと方向転換する場合を考えてみましょう.ここで,辺$AB$から辺$BC$に行くときに,プールを泳ぐのが速いのか,辺を伝うのが速いのかを考慮する必要があります.図12のように点$E,F$をとり,$CE=e,CF=f$としてみます.
このとき,プールでショートカットを試みると$\sqrt{e^2+f^2}$秒かかります.縁を歩くと$\frac{1}{2}(e+f)$秒かかります.
$$ (\sqrt{e^2+f^2})^2-(\frac{1}{2}(e+f))^2=e^2+f^2-\frac{1}{4}(e^2+f^2+2ef)=\frac{1}{4}\left(3e^{2}+3f^{2}-2ef\right) \ge 0 $$
以上のようになるので縁を歩く方が速いですね.よって,$X$までに到達する時間は$5+\frac{q}{2}+\frac{\sqrt{3}}{2}\left(10-p\right)$秒となります.
 プールでショートカットはできるのか?
プールでショートカットはできるのか?
 プールサイドは走ると危ないですよ。
プールサイドは走ると危ないですよ。
仕上げ
ということである点$X$に行くまでにかかる時間は,$\min\left(\frac{p}{2}+\frac{\sqrt{3}q}{2},\ 5+\frac{q}{2}+\frac{\sqrt{3}}{2}\left(10-p\right)\right)$となります.ここで,$0 \le p,q \le10, \ p \ge q$を満たすことに注意しましょう.
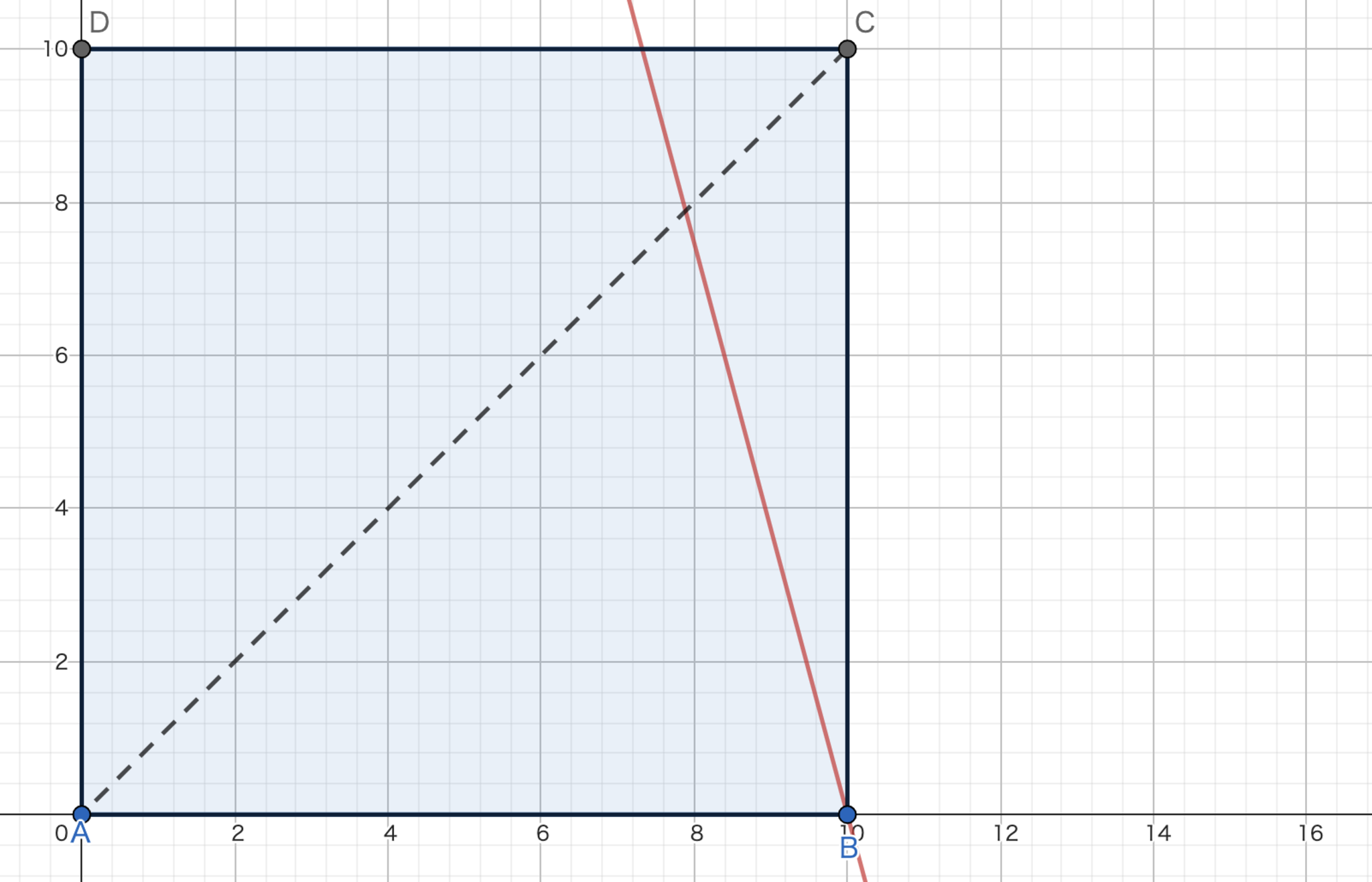
この$\min$関数についてもう少し詳しく考えてみます.大小関係が分かれば$\min$関数が外せるので大小関係に注目してみましょう.$\min\left(\frac{p}{2}+\frac{\sqrt{3}q}{2},\ 5+\frac{q}{2}+\frac{\sqrt{3}}{2}\left(10-p\right)\right)$の二つをイコールで結んで線分を作ればそこがcase1を用いるか,case2を用いるかの境界線になりますよね.ちなみに,式は以下のようになります.
$$ \frac{x}{2}+\frac{\sqrt{3}y}{2}=5+\frac{y}{2}+\frac{\sqrt{3}}{2}\left(10-x\right) $$
case1の場合はかかる時間が$\frac{p}{2}+\frac{\sqrt{3}q}{2}$秒だったので$p,q$に関して単調増加であるから最も時間がかかる点は右上の境界線上にあることがわかり,その中で最も時間がかかるのは境界線と対角線の交点となります.
case2の場合はかかる時間が$5+\frac{q}{2}+\frac{\sqrt{3}}{2}\left(10-p\right)$秒だったので$p$に関して単調減少,$q$に関して単調増加であるから最も時間がかかる点は対角線上にあることがわかりその中で最も時間がかかるのは境界線と対角線の交点となります.よって,最も時間がかかる点がわかりました!
あとはここまでの到達時間を計算して,$\frac{3}{5}\left(3+2\sqrt{3}\right)$秒となります.いやぁ〜計算が少し重かった.お疲れ様でした!
 境界線
境界線
終わりに
お疲れ様でした.書いていてとっても楽しい記事でした.ここまで読んでくださった皆さん,本当にありがとうございました!
