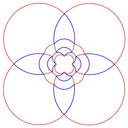
混線内接円を反転

720

はじめに

　curvilinear incircle の angle chase がややこしく，手順を忘れたり，頭が混線したりしたので，mixitilinear incircle (以下，「混線内接円」) のいくつかの性質を，反転で(curvilinear incircleなしに)示します．

準備

　混線内接円を定義します．

混線内接円

　$\triangle ABC$において，半直線$AB,AC$に接し，$ABC$の外接円に内接する円を ($\angle A$内の) 混線内接円という．

　今回の記事では，「$P_1,P_2, \dots, P_n$ の外接円」を$(P_1P_2 \dots P_n)$と略記します．

　必要な点と円を定義します．

基本的な点・円の名前

　$\triangle ABC$において，

$\Gamma$: 外接円
$\omega$: 内接円
$\omega _A$:$\angle A$内の傍接円
$\Omega _A$:$\angle A$内の混線内接円
$I$: 内心
$I _A$ : $\angle A$内の傍心
とする．

接点の名前

$\Omega _A$ と$AC,AB,\Gamma$の接点をそれぞれ$K_1,K_2,T$とする．
$\omega _A$ と$AB,AC,BC$の接点をそれぞれ${K_1}^{\prime},{K_2}^{\prime},E$とする．

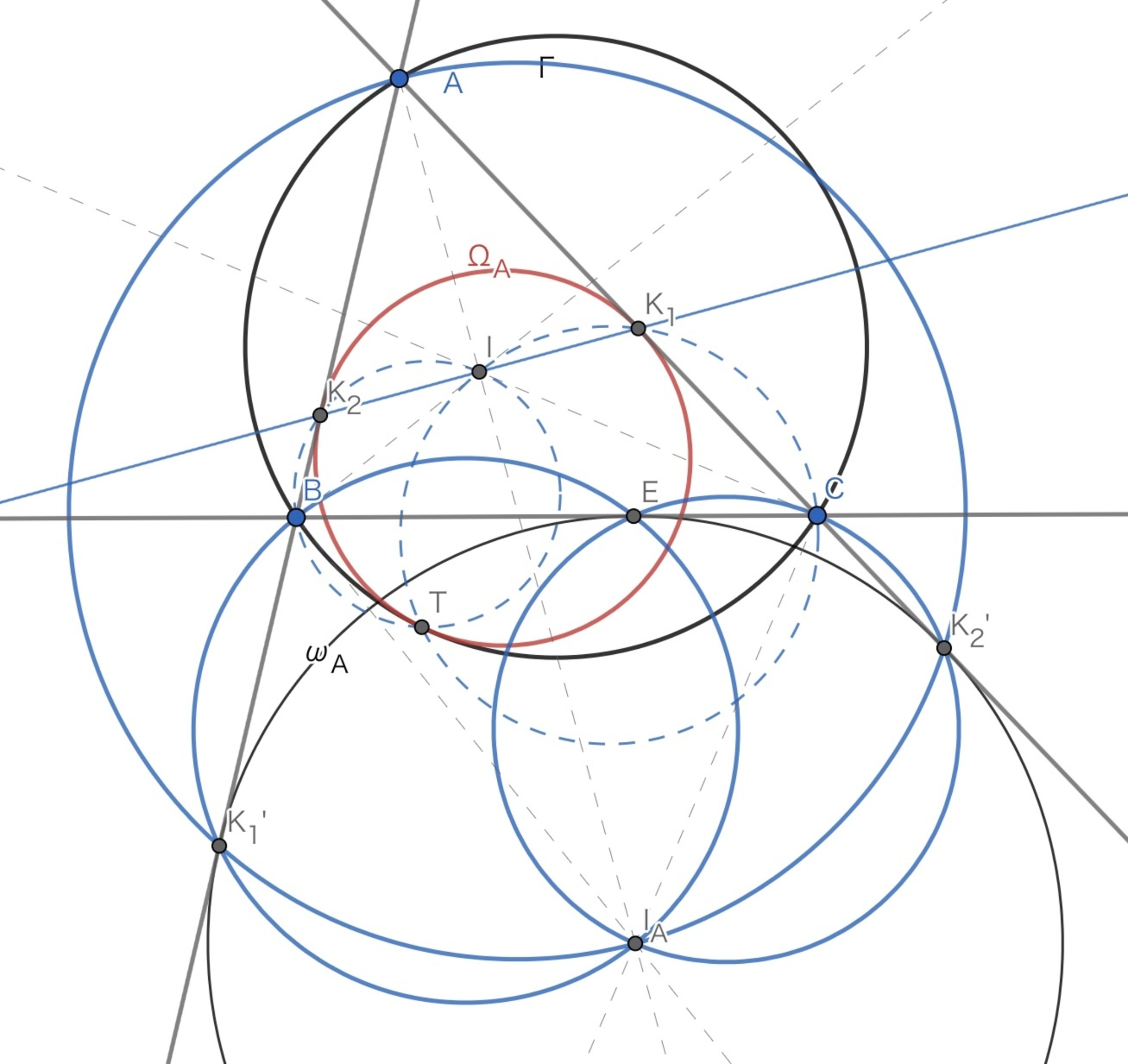
こんな感じの図になります．
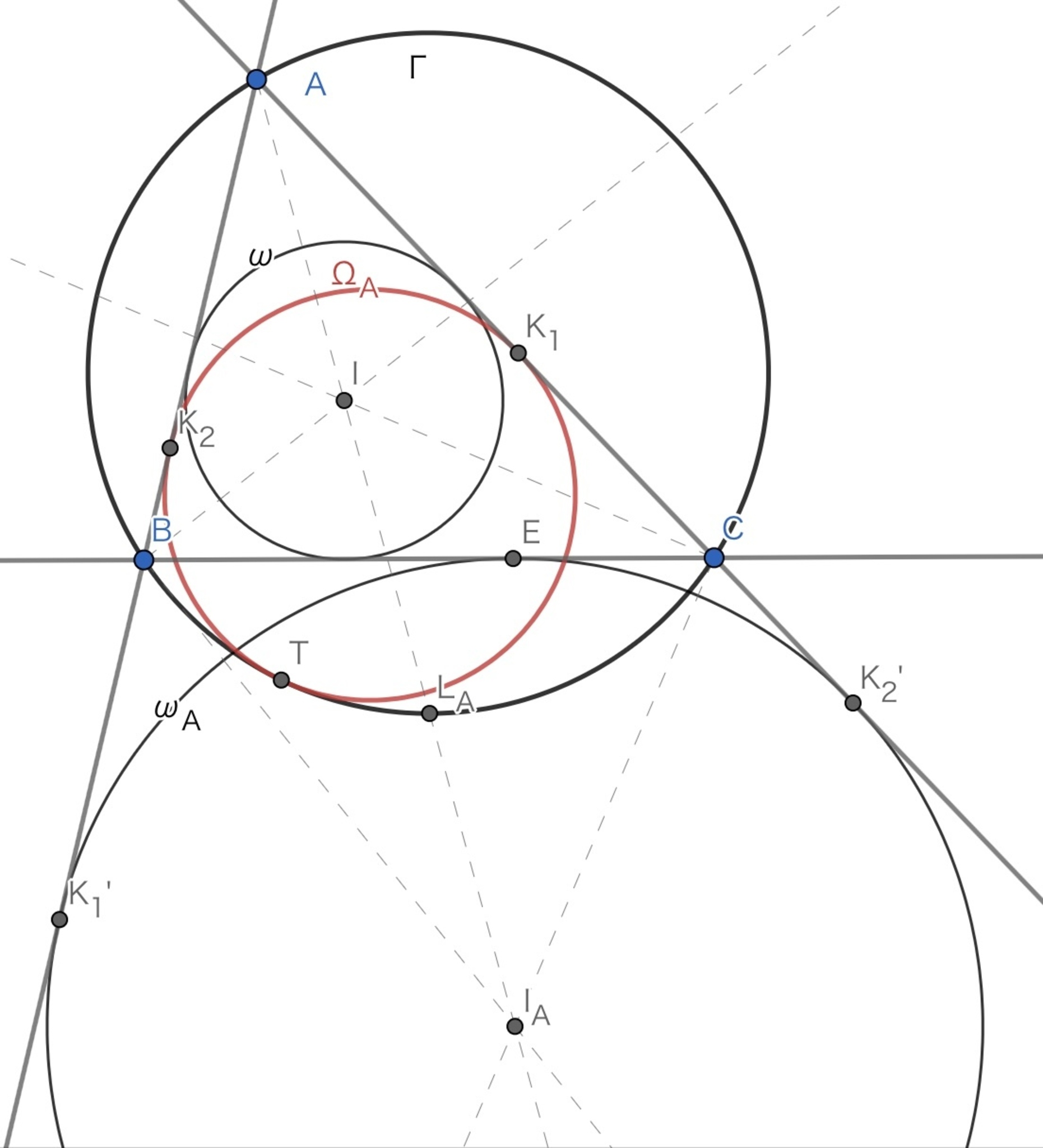定義した点

最終的にはもっと混線した図になります．
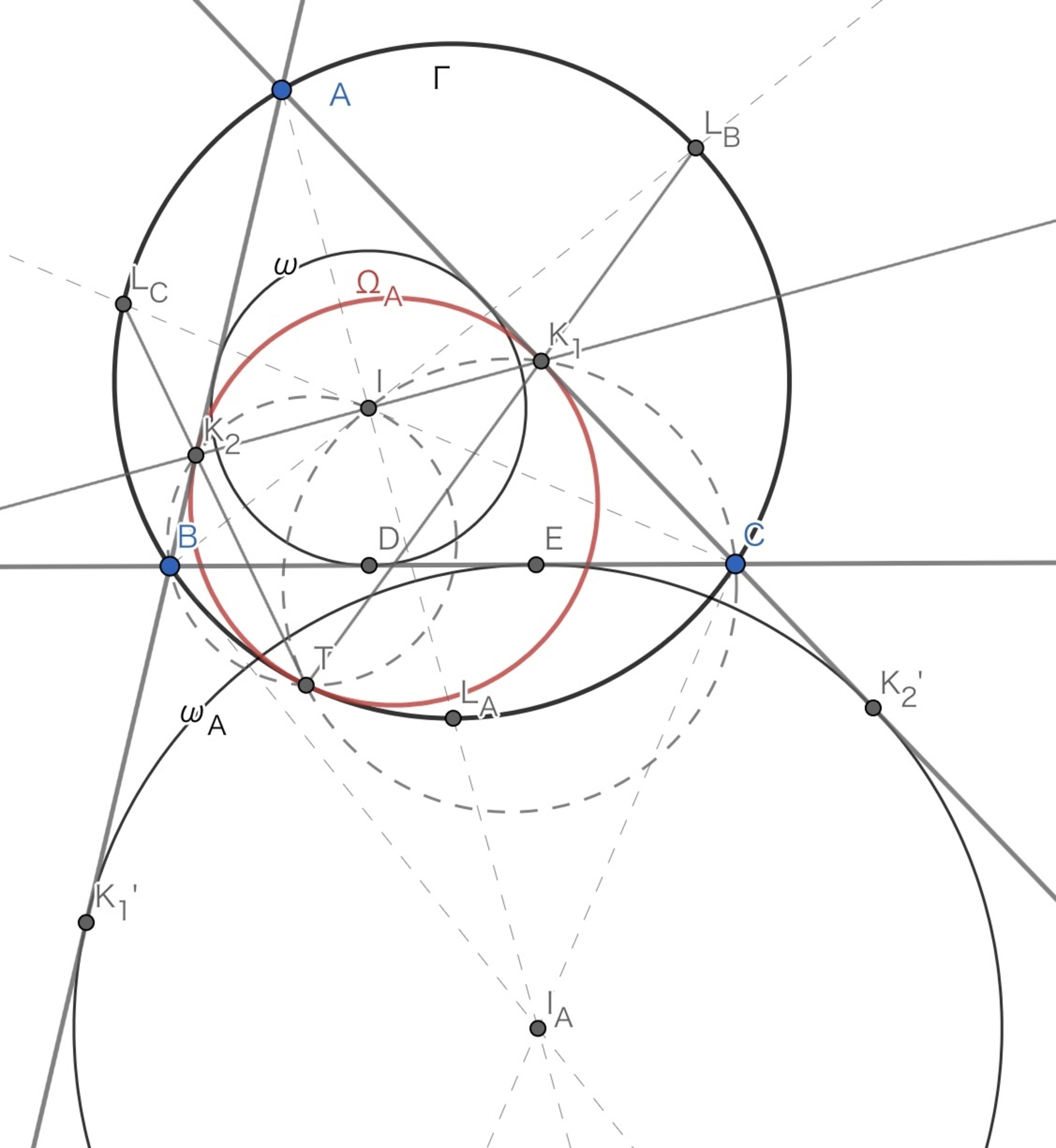ごちゃごちゃした図

反転！

　ユークリッド平面に無限遠点$P_{\infty}$を付け加えます．
中心$A$，半径$\sqrt{AB \cdot AC}$ での反転を行う写像を$f_1$，直線$AI$での鏡映を行う写像を$f_2$とすると，$f_2(f_1(B))=C,f_2(f_1(C))=B$です．
　$f_1$と$f_2$は大体一緒に使うので，$f_2(f_1(X))$を$X^{\star}$と書くことにします．
また，集合$\Sigma$の像$f_2[f_1[\Sigma]]$$({}=\{X^{\star}|X \in \Sigma\})$も${\Sigma}^{\star}$と書きます．

${\Omega _A}^{\star} = \omega _A$

$B^{\star}=C,C^{\star}=B$より，$\Gamma = (ABC)$は直線$BC$にうつる．
よって，${\Omega _A}^{\star}$は直線$AC,AB,BC$に，それぞれ${K_1}^{\star},{K_2}^{\star},E$で接する．
$\Omega _A$は$\angle BAC$の内側に位置し，反転と鏡映でこれは変わらない．
$AK_1 \lt AC$より，$AB \lt {AK_1}^{\star}$であるから，${\Omega _A}^{\star}$は$\triangle ABC$の外側に存在する．
したがって，${\Omega _A}^{\star}$は$\triangle ABC$の$\angle A$内の傍接円．

命題 1

${K_1}^{\star}={K_1}^{\prime}$
${K_2}^{\star}={K_2}^{\prime}$
${T}^{\star}=E$

$I^{\star}=I_A$

$\angle If_2(C)I_A = \angle ICI_A = \angle IBI_A = 90^{\circ}$より，$I,B,C,f_2(C),I_A$は共円．
方べきの定理より，$AI \cdot AI_A = AB \cdot Af_2(C) = AB \cdot AC$で，$A,I,I_A$は共線であるから，$I^{\star} =f_2(f_1(I)) = f_2(I_A) = I_A$

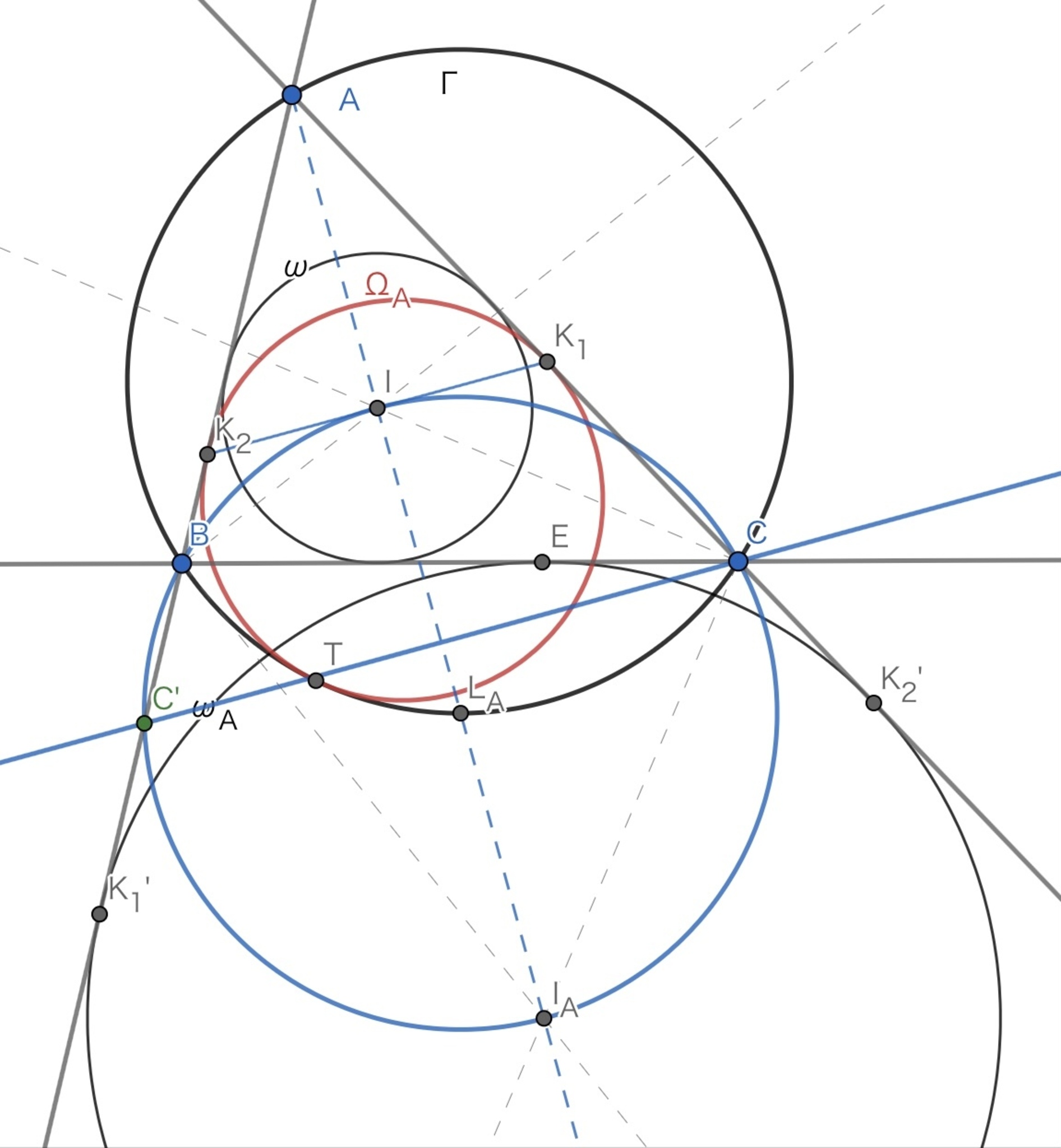共線にして方べき

これを使って，$I$が絡む共円性・共線性を示します．

$(a)$ $K_1,I,K_2$は共線で，特に$K_1,I,K_2,P_{\infty}$は調和点列．
$(b)$ $I,K_2,B,T$は共円で，特に四角形$IK_2BT$は調和四角形．
$(c)$ $I,K_1,C,T$は共円で，特に四角形$IK_1CT$は調和四角形．

$A{K_1}^{\prime} \perp {K_1}^{\prime}I_A, A{K_2}^{\prime} \perp {K_2}^{\prime}I_A$であるから，
四角形${K_1}^{\prime}I_A{K_2}^{\prime}A,$$I_A{K_2}^{\prime}CE,$$I_A{K_1}^{\prime}CE$は，それぞれ，$AI_A,$$BI_A,$$CI_A$を直径とする円に内接する．
さらに，これらはそれぞれ外接円の直径を軸として対称であるから，調和四角形である．
よって，反転して$(a),(b),(c)$が得られる．
直角による共円

直線$TK_1,BI$と円$\Gamma$は共点．
直線$TK_2,CI$と円$\Gamma$は共点．

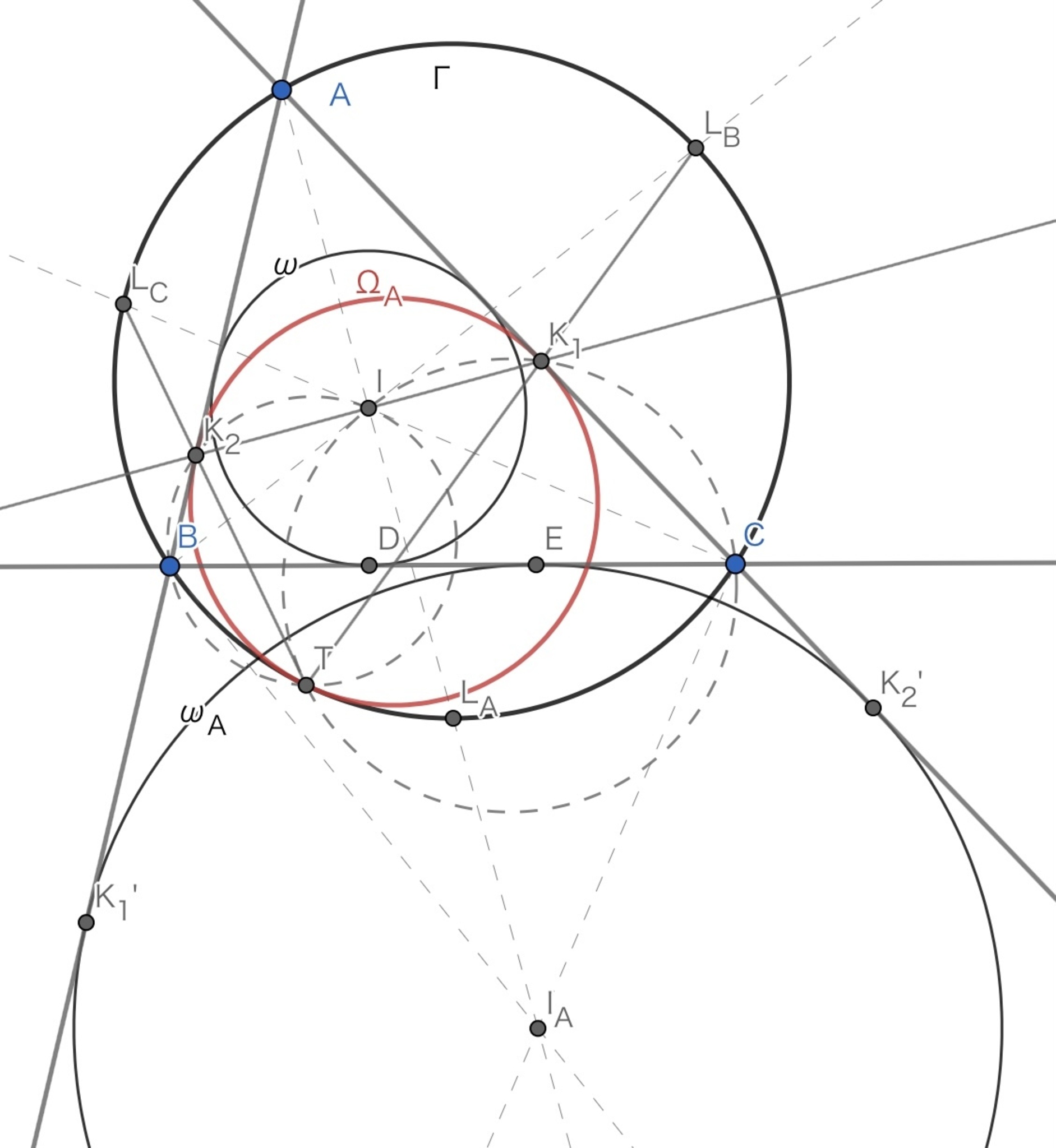共点性

直線$BI$と円$\Gamma$の交点の，$B$でない方を$L_B$とおく．
直線$CI$と円$\Gamma$の交点の，$C$でない方を$L_C$とおく．
点$T$を中心として，$\Omega_A$を$\Gamma$にうつすような相似拡大で，$AB$は$AB$に平行な$\Gamma$の接線に，$AC$は$AC$に平行な$\Gamma$の接線にうつる．
これらは，それぞれ$L_C,L_B$における$\Gamma$の接線であるから，この相似拡大は，$K_1,K_2$をそれぞれ$L_B,L_C$にうつす．
したがって，$T,K_1,L_B$は共線，$T,K_2,L_C$は共線．