Metachick's Math Problems 001~020

352

はじめに

今回は過去に作った数学の問題の一部をまとめてみました.とりあえず,20問です!

・難易度：★☆☆☆☆〜★★★★★までの五段階評価になっています.(高難易度の問題はストックしてあったりするので少ないです...)
・出題範囲：データの分析などを除く数学Ⅲ以前の知識に加え,グラフ理論などやや発展的な内容も必要になります.(ただし,ほとんどが数学ⅡB以前の知識で解けます)
・解答：解答は一部労力削減のために,「有名事実より」などと書くことがあります。全体的に行間が広いかもしれませんが,ご了承ください.わからないところがありましたら,TwitterのDMかコメント欄にて質問していただければ解答します.

問題

MMPs001/★★☆☆☆

$0$ 以上 $1$ 未満の実数からなる集合 $G$ の任意の二要素 $a, b$ の和 $a + b$ の小数部分も $G$ の要素になる.このとき、 $G$ としてありうるもののうち,要素数が $n$ 個であるようなものを全て求めよ.

$n = 1$ ならば $G = 0$ のみが解であることが容易にわかるので $n \neq 1$ とする. $G$ の要素を $x_{1}, x_{2}, \dots, x_{n}$ とする.このとき, $G$ のある $0$ でない要素をとることができるのでそれを $x$ とする. ${x + x_{1}, x + x_{2}, \dots, x + x_{n}}$ も $G$ である.

よって, $x_{1} + x_{2} + \dots + x_{n} \equiv (x + x_{1}) + (x + x_{2}) + \dots + (x + x_{n}) (\mod 1)$ であるから, $n x \equiv 0 (\mod 1)$ である.よって, $x$ は $\frac{k}{n}$ の形で表される.逆に, $\frac{0}{n}$ ~ $\frac{n - 1}{n}$ までの $n$ 個の数字は解を満たすので $G = {0, \frac{1}{n}, \frac{2}{n}, \dots, \frac{n - 1}{n}}$ が唯一の解となる.

複素数による置換の方が見えやすそう

$G$ の要素を $x_{1}, x_{2}, \dots, x_{n}$ とし,絶対値が $1$ で偏角が $2 x_{i} π$ の複素数を $y_{i}$ とする.集合 $G^{'}$ を $y_{1}, y_{2}, \dots, y_{n}$ からなる集合とすれば $G^{'}$ の任意の二つの要素の積も $G^{'}$ の要素となっていることがわかる.

$G^{'}$ のある要素 $z$ をとれば, $G^{'}$ の要素を $z y_{1}, z y_{2}, \dots, z y_{n}$ と表すこともできるので $y_{1} \times y_{2} \times \dots \times y_{n} = z^{n} \times y_{1} \times y_{2} \times \dots \times y_{n}$ となるから $z^{n} = 1$ を得る.よって、 $G^{'}$ の任意の要素は $1$ の $n$ 乗根となる必要がある。逆に, $1$ の $n$ 乗根 $n$ 個は条件を満たすから $G^{'}$ は $1$ の $n$ 乗根の集合である.よって,解答は $G = {0, \frac{1}{n}, \frac{2}{n}, \dots, \frac{n - 1}{n}}$ となる.

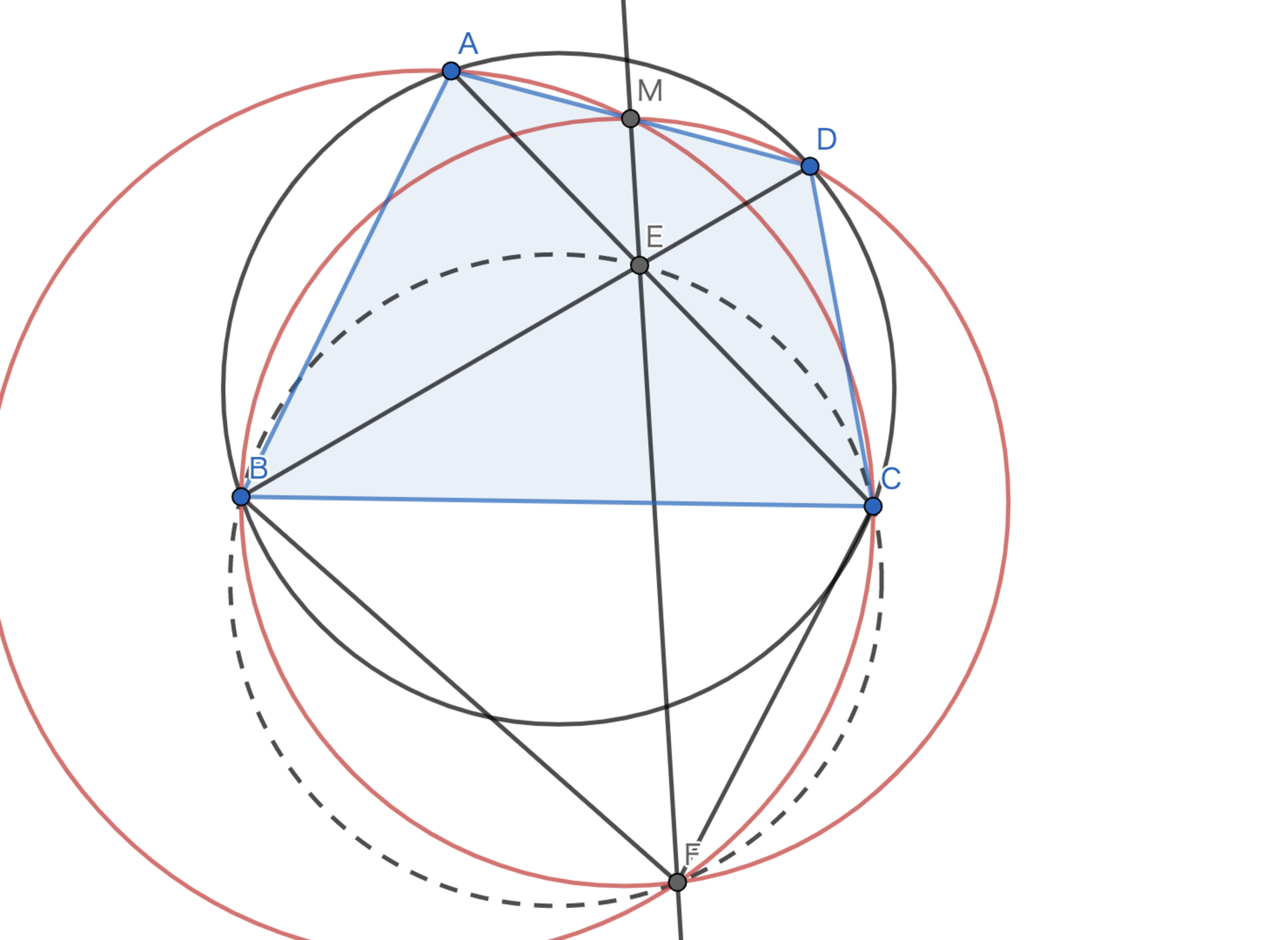
MMPs002/★★★☆☆

放物線 $c_{1}$ : $y = x^{2} - 4$ と放物線 $c_{2}$ : $x = y^{2} - 3$ の交点を第一象限から反時計回りにそれぞれ $A, B, C, D$ とし, $A C$ と $B D$ の交点を $E$ とする. $A B$ の中点を $M$ , $C D$ の中点を $N$ とするとき, $∠ B M E = ∠ C N E$ を示せ.

有名事実より, $A, B, C, D$ は共円である.(これは座標を計算して方べきの定理などを用いればよい.)よって,円に内接する四角形 $A B C D$ においてその対角線の交点を $E$ とし, $A B, C D$ の中点 $M, N$ としたとき, $∠ B M E = ∠ C N E$ であることを示せば良い.

簡単な角度計算により,示すべきことは直線 $M E$ が $△ C D E$ の類似中線であることを示すことと同値であることがわかる.ここで, $△ B E C$ の外接円と $M E$ の交点を $F$ とすれば,簡単な角度計算により $△ A M E ∽ △ F C E, △ D M E ∽ △ F B E$ を得る.よって,これらの比を考えれば $E C : C F = E M : M A$ , $E B : B F = E M : M D$ を得る.また, $M$ が中点であるので $E C : C F = E B : B F$ であるから $E C \cdot B F = C F \cdot E B$ を得る.有名事実としてこれを満たす円に内接する四角形は調和四角形であるから直線 $M E$ は $△ E B C$ の $E - S y m m e d i a n$ である.よって,題意は示された.

MMPs002 MMPs002

MMPs003/★★☆☆☆

以下の式を整数係数の範囲で因数分解せよ.

$x^{4} + y^{4} + z^{4} + w^{4} + (x y + y z + z w + w x + x z + y w) (x^{2} + y^{2} + z^{2} + w^{2}) + 4 x y z w$

解答

$t$ に関する以下の方程式を考える.
$t^{4} - (x + y + z + w) t^{3} + (x y + y z + z w + w x + x z + y w) t^{2} - (x y z + y z w + z w x + w x y) t + x y z w = 0$
この方程式に $t = x, y, z, w$ を代入したものを辺々足すことによって以下の式を得る.
$x^{4} + y^{4} + z^{4} + w^{4} + (x y + y z + z w + w x + x z + y w) (x^{2} + y^{2} + z^{2} + w^{2}) + 4 x y z w = (x + y + z + w) (x^{3} + y^{3} + z^{3} + w^{3} + y z w + z w x + w x y + x y z)$
右辺の $(x^{3} + y^{3} + z^{3} + w^{3} + y z w + z w x + w x y + x y z)$ は既約なので $(x + y + z + w) (x^{3} + y^{3} + z^{3} + w^{3} + y z w + z w x + w x y + x y z)$ である.

MMPs004/★☆☆☆☆

$f (x)$ を $x$ の $200$ 以上の約数の個数とする.このとき以下の値を計算せよ.

f (1) + f (2) + \dots + f (1000)

$200$ 以上の整数が何回寄与するかを考えれば良い.例えば $200$ は $f (200), f (400), \dots, f (1000)$ の計 $5$ 回数えられると言った具合である.
$\sum_{n = 200}^{1000} ⌊ \frac{1000}{n} ⌋ = 5 \cdot 1 + 4 \cdot 50 + 3 \cdot 83 + 2 \cdot 167 + 1 \cdot 500 = 1228$

MMPs005/★★☆☆☆

正実数 $A, B, C$ は $A + B + C = π$ を満たす.この時,以下の不等式を示せ.
$\sin A \cos B \cos C + \sin B \cos C \cos A + \sin C \cos A \cos B \leq \frac{3 \sqrt{3}}{8}$

$\begin{aligned} \sum_{c y c}^{} \sin A \cos B \cos C & = \sin A \cos B \cos C + \sin B \cos C \cos A + \sin C \cos A \cos B \\ = (\sin A \cos B \cos C + \sin B \cos C \cos A + \sin C \cos A \cos B) \cdot \frac{\cos A \cos B \cos C}{\cos A \cos B \cos C} \\ = \cos A \cos B \cos C (\tan A + \tan B + \tan C) \\ = \cos A \cos B \cos C \cdot \tan A \tan B \tan C \\ = \sin A \sin B \sin C \end{aligned}$

$\frac{\sin A + \sin B + \sin C}{3} \geq \sqrt[3]{\sin A \sin B \sin C}$

両辺を三乗すると,

${(\frac{\sin A + \sin B + \sin C}{3})}^{3} \geq \sin A \sin B \sin C$

等号成立は, $A = B = C = \frac{π}{3}$ の時. $s i n X$ は $0 < X < π$ で上に凸だから左辺をイェンゼンの不等式を用いて左辺を評価すると

${(\frac{3 \sin \frac{A + B + C}{3}}{3})}^{3} \geq {(\frac{\sin A + \sin B + \sin C}{3})}^{3}$

が成立する.これを整理すると,

$\frac{3 \sqrt{3}}{8} \geq {(\frac{\sin A + \sin B + \sin C}{3})}^{3} \geq \sin A \sin B \sin C = \sum_{c y c}^{} \sin A \cos B \cos C$

この時,全ての不等号について等号成立条件は $A = B = C = \frac{π}{3}$ で一致しているため題意は示された.

MMPs006/★★☆☆☆

正実数 $a, b, c$ は $a + b + c = a b c$ を満たす.このとき,以下の不等式を示せ.
$\frac{{(a b c)}^{2}}{(a^{2} + 1) (b^{2} + 1) (c^{2} + 1)} \leq \frac{27}{64}$

$\tan A = a, \tan B = b, \tan C = c$ となるように $A, B, C$ を定める.ただし, $0 \leq A, B, C < 2 π$ である.この時,条件より, $\tan A + \tan B + \tan C = \tan A \tan B \tan C$ であるから, $A + B + C = π$ となる.

$\begin{aligned} \frac{{(\tan A \tan B \tan C)}^{2}}{(\tan^{2} A + 1) (\tan^{2} B + 1) (\tan^{2} C + 1)} & = {(\sin A \sin B \sin C)}^{2} \\ \leq {(\frac{\sin A + \sin B + \sin C}{3})}^{6} ∵ (A M - G M) \\ \leq {(\frac{3 \sin (\frac{A + B + C}{3})}{3})}^{6} ∵ (J e n s e n) \\ = \sin^{6} \frac{π}{3} \\ = \frac{27}{64} \end{aligned}$

不等号の等号成立条件は全て一致しているため題意は示された.

MMPs007/★★☆☆☆

$n, k$ を $2$ 以上の正整数とする. $n^{k!} - 1$ は $k$ 未満の任意の素数 $p$ に対して $p$ で割って $1$ 余る $1$ でない約数を持つことを示せ.

$\begin{aligned} n^{k!} - 1 & = (n - 1) (n^{k! - 1} + n^{k! - 2} + \dots + n^{2} + n + 1) \end{aligned}$
である.ここで $p$ を $k$ 未満の素数とすると, $(n^{k! - 1} + n^{k! - 2} + \dots + n^{2} + n + 1)$ は $S = (n^{p} + n^{p - 1} + \dots + n^{2} + n^{1} + 1)$ , $S^{'} = (n^{p - 1} + n^{p - 2} + \dots + n^{2} + n^{1} + 1)$ を約数に持つ.ここで, $n \equiv 1 (m o d p)$ の時 $S \equiv 1 (m o d p)$ であり, $n ≢ 1 (m o d p)$ の時 $S^{'} = \frac{n^{p} - 1}{n - 1} \equiv \frac{n - 1}{n - 1} = 1 (m o d p)$ となる.これらは明らかに $1$ ではないので題意は示された.

(約数に持つことは因数分解を考えればわかります.これは項を $i$ 個ずつまとめる方法での因数分解を考えれば良いですね.)

階乗進法を用いた別解

$\begin{aligned} n^{k!} - 1 & = (n - 1) (n^{k! - 1} + n^{k! - 2} + \dots + n^{2} + n + 1) \\ = (n - 1) (n^{1!} + 1) (n^{2 \cdot 2!} + n^{2!} + 1) \dots (n^{(k - 1) (k - 1)!} + n^{(k - 2) (k - 1)!} + \dots + n^{2 (k - 1)!} + n^{(k - 1)!} + 1) \end{aligned}$
ただし,最後の変形に関しては階乗進法の一意性を用いた.

$n^{p!} - 1$ の約数 $S = n^{p \cdot p!} + n^{(p - 1) p!} + \dots + n^{2 \cdot p!} + n^{p!} + 1$ を考える.このとき,フェルマーの小定理より $n$ が $p$ の倍数でないならば $n^{p!} \equiv 1 (m o d p)$ であるから, $S \equiv 1 (m o d p)$ が従う. $n$ が $p$ の倍数であるなら明らかに $S \equiv 1 (m o d p)$ である.よって題意は示された.

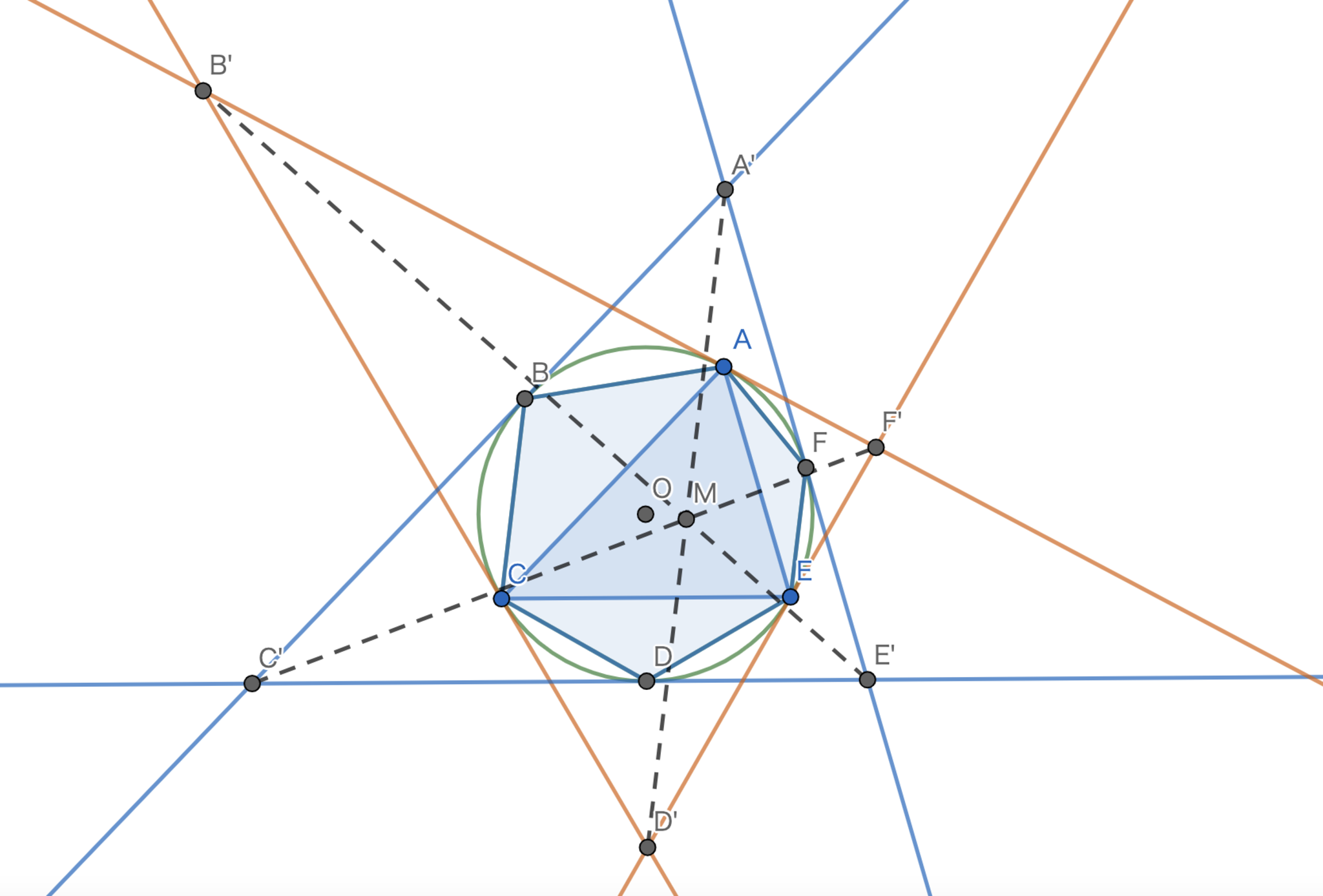
MMPs008/★★★☆☆

円 $Ω$ に内接する六角形 $A B C D E F$ は $| A B | = | B C |, | C D | = | D E |, | E F | = | F A |$ を満たす. $Ω$ の $A, B, C, D, E, F$ における接線をそれぞれ $L_{A}, L_{B}, L_{C}, L_{D}, L_{E}, L_{F}$ とする. $L_{A}$ と $L_{C}$ の交点を $B^{'}$ , $L_{B}$ と $L_{D}$ の交点を $C^{'}$ , $L_{C}$ と $L_{E}$ の交点を $D^{'}$ , $L_{D}$ と $L_{F}$ の交点を $E^{'}$ , $L_{E}$ と $L_{A}$ の交点を $F^{'}$ , $L_{F}$ と $L_{B}$ の交点を $A^{'}$ とするとき, $A^{'} D^{'}, B^{'} E^{'}, C^{'} F^{'}$ は一点で交わることを示せ.

難易度に関して悩みました.初等的に解こうとすると難易度は高くなってしまいますが,複素では簡単に解けるのでここでは簡単な解法に合わせる方針で行きます.

複素座標

方針:うまく三点 $A, C, E$ の座標を定めて使う文字数を減らす.(一度は初等的に考えてみましょう.すると,角の二等分線が登場することに気付けると思います.そこで,うまく座標設定ができることを思いつくでしょう.)
$A (a^{2}) B (- a c) C (c^{2}) D (- c e) E (e^{2}) F (- e a)$
となるようにうまく座標を定める.このとき
$A^{'} (- \frac{2 a c e}{c + e}) B^{'} (\frac{2 a^{2} c^{2}}{a^{2} + c^{2}}) C^{'} (- \frac{2 a c e}{e + a}) D^{'} (\frac{2 c^{2} e^{2}}{c^{2} + e^{2}}) E^{'} (- \frac{2 a c e}{a + c}) F^{'} (\frac{2 e^{2} a^{2}}{e^{2} + a^{2}})$
が得られる. $A^{'} D^{'}$ の式を考えていく.このとき, $\bar{A^{'}} (- \frac{2}{a (c + e)}), \bar{D^{'}} (\frac{2}{c^{2} + e^{2}})$ であることに留意して,
$A^{'} D^{'} : (\bar{A^{'}} - \bar{D^{'}}) z - (A^{'} - D^{'}) \bar{z} = \bar{A^{'}} D^{'} - A \bar{D^{'}} ⟺ - \frac{2 c^{2} + 2 e^{2} + 2 a c + 2 a e}{a (c + e) (c^{2} + e^{2})} z + \frac{2 c e (a c^{2} + a e^{2} + c^{2} e + c e^{2})}{(c + e) (c^{2} + e^{2})} \overset{―}{z} = - \frac{4 c^{2} e^{2}}{a (c + e) (c^{2} + e^{2})} + \frac{4 a c e}{(c + e) (c^{2} + e^{2})} ⟺ - (a c + a e + c^{2} + e^{2}) z + a c e (a c^{2} + a e^{2} + c^{2} e + c e^{2}) \overset{―}{z} = 2 a^{2} c e - 2 c^{2} e^{2}$
となる.ここで, $z = - (a c + c e + e a)$ を代入する.(内心)
$(a c + a e + c^{2} + e^{2}) (a c + c e + e a) - a c e (a c^{2} + a e^{2} + c^{2} e + c e^{2}) (\frac{1}{a c} + \frac{1}{c e} + \frac{1}{c a}) = 2 a^{2} c e - 2 c^{2} e^{2}$
が成り立つので $A^{'} D^{'}$ は内心を通る.このとき,対称性より $B^{'} E^{'}, C^{'} F^{'}$ も内心を通るので三直線は一点,特に内心で交わることが示された.

MMPs008 MMPs008

MMPs009/★☆☆☆☆

四角形 $A B C D$ において, $A B$ の中点を $M_{A B}$ などと表すとき, $M_{A B} M_{C D}, M_{B C} M_{D A}, M_{A C} M_{B D}$ は一点で交わることを示せ.

$M_{A B} M_{C D}, M_{B C} M_{D A}$ の交点を $P$ とする.中点連結定理より,四角形 $M_{A B} M_{B C} M_{C D} M_{D A}$ は平行四辺形となるので $P$ は $M_{A B} M_{C D}, M_{B C} M_{D A}$ の中点である.

$M_{A B} M_{C D}, M_{A C} M_{B D}$ の交点を $Q$ とする.中点連結定理より,四角形 $M_{A B} M_{A C} M_{C D} M_{B D}$ は平行四辺形となるので $Q$ は $M_{A B} M_{C D}, M_{A C} M_{B D}$ の中点である.よって, $P = Q$ であるから題意は示された.

複素平面を用いた別解

複素平面上に $A (a), B (b), C (c), D (d)$ とおく.このとき, $M_{A B} M_{C D}, M_{B C} M_{D A}, M_{A C} M_{B D}$ は全て $\frac{a + b + c + d}{4}$ を通るので題意は示された.

MMPs010/★☆☆☆☆

$a_{1} = a_{2} = 2$ なる数列 ${a_{n}}$ は以下を満たす.数列 ${a_{n}}$ の一般項を求めよ.
$a_{n + 1}^{100} = a_{n}^{100} + a_{n - 1}^{100} + \dots + a_{1}^{100}$

$a_{n + 1}^{100} = 2 a_{n}^{100}$ であるので $b_{n} = a_{n}^{100}$ 　などとして計算すれば一般項は $\begin{array}{r} a_{n} = {\begin{cases} \sqrt[100]{2^{n + 98}} (n \neq 1) \\ 2 (n = 1) \end{cases} \end{array}$ となる.

MMPs011/★★★☆☆

$k$ を正整数とする.このとき,以下の不等式を示せ.
$\sum_{n = 1}^{6 k} \sqrt{1 + n^{2}} > \sum_{n = 1}^{3 k} \sqrt{4 + {(4 n - 1)}^{2}} > \sum_{n = 1}^{k} \sqrt{36 + {(36 n - 15)}^{2}}$

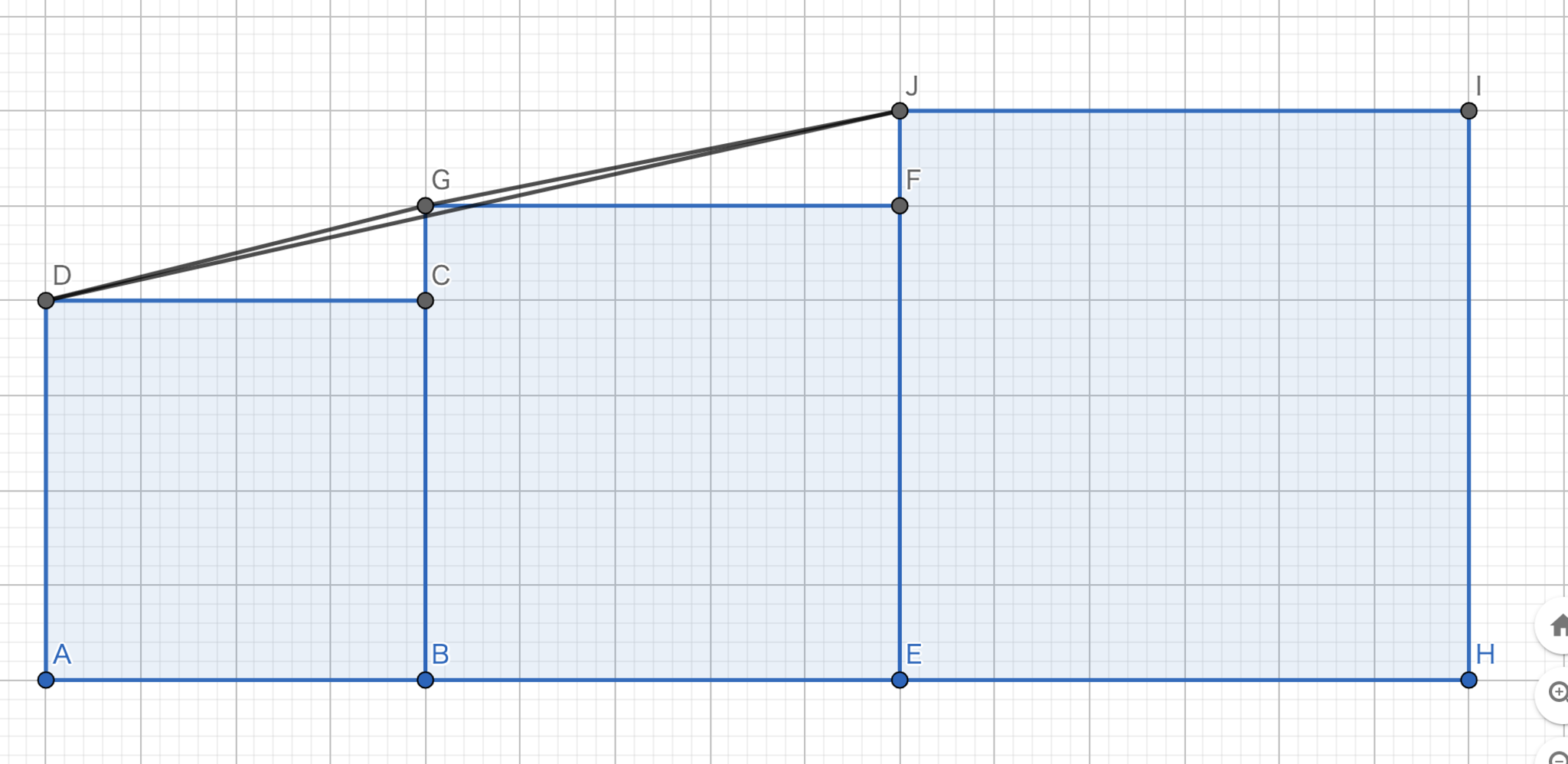
$左辺 > 中辺$ が成り立つことは
$\begin{array}{r} \sum_{n = 1}^{3 k} (\sqrt{{(2 n - 1)}^{2} + 1} + \sqrt{{(2 n)}^{2} + 1}) > \sum_{n = 1}^{3 k} \sqrt{{(4 n - 1)}^{2} + 4} \end{array}$
が成り立つことと同値である.したがって, $\sqrt{{(2 n - 1)}^{2} + 1} + \sqrt{{(2 n)}^{2} + 1} > \sqrt{{(4 n - 1)}^{2} + 4}$ を示せば十分である.上の図において, $| A B | = 2 n - 1, | B E | = 2 n$ とすると $| D G | = \sqrt{{(2 n - 1)}^{2} + 1}, | G J | = \sqrt{{(2 n)}^{2} + 1}, | D J | = \sqrt{{(4 n - 1)}^{2} + 4}$ となる.三角不等式より, $| D G | + | G J | > | D J |$ であるから $左辺 > 中辺$ は示された.

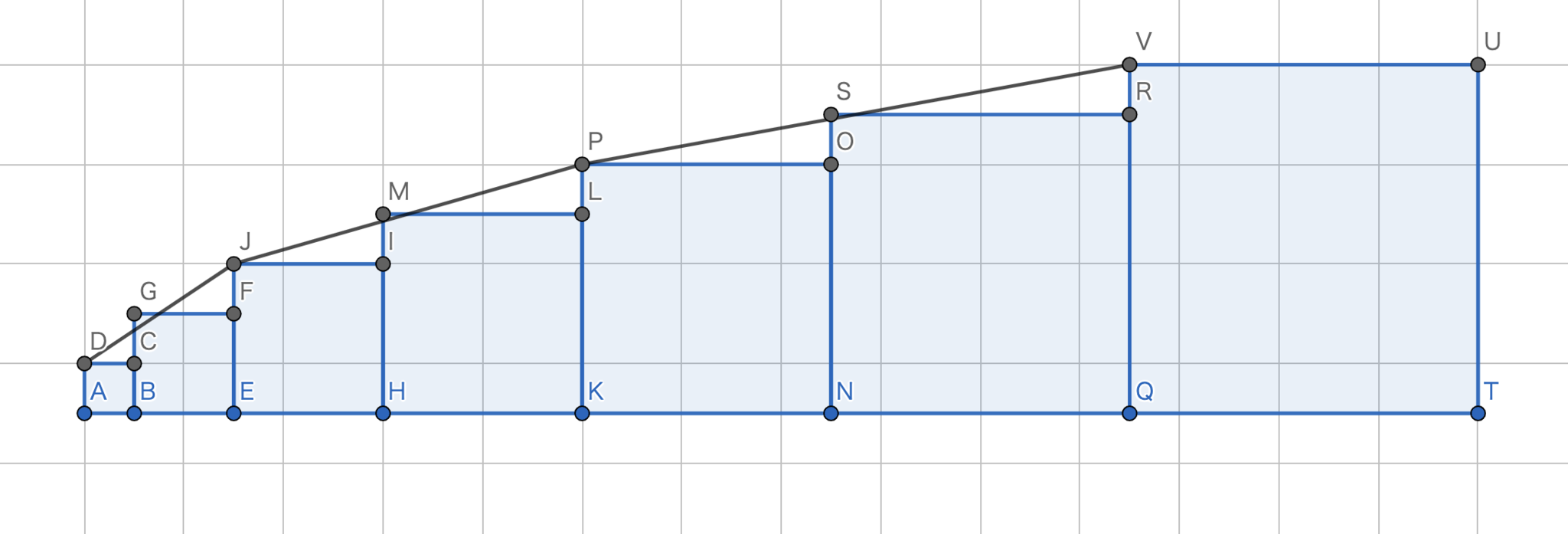
$中辺 > 右辺$ が成り立つことは
$\sum_{n = 1}^{k} (\sqrt{{(4 (3 n - 2) - 1)}^{2} + 4} + \sqrt{{(4 (3 n - 1) - 1)}^{2} + 4} + \sqrt{{(4 (3 n) - 1)}^{2} + 4}) > \sum_{n = 1}^{k} \sqrt{36 + {(36 n - 15)}^{2}}$
が成り立つことと同値である.したがって, $\sqrt{{(12 n - 9)}^{2} + 4} + \sqrt{{(12 n - 5)}^{2} + 4} + \sqrt{{(12 n - 1)}^{2} + 4} > 3 \sqrt{{(12 n - 5)}^{2} + 4}$ を示せば十分である.下の図においても $左辺 > 中辺$ の証明と同様に考えると
$(中辺) = | D G | + | G J | + | J M | + | M P | + | P S | + | S V |$ , $(右辺) = | D V |$
となって,三角不等式より $中辺 > 右辺$ が示された.

したがって,題意は示された.

MMPs011-1

MMPs011-2

MMPs012/★★☆☆☆

連続する素数 $p, q, r, s, t$ は $p < q < r < s < t$ を満たす.このとき,以下の不等式を示せ.ただし,正整数 $n$ の正の約数の個数を $d (n)$ で表す.

$d (p + q) + d (q + r) + d (r + s) + d (s + t) \geq 18$

$a, b$ を連続奇素数とする. $a + b$ は偶数であり, $a, b$ は連続素数なので, $a + b = 2 c$ となる素数 $c$ は存在しない.従って, $a + b$ の素因数の個数は $3$ つ以上である.(重複も含めて)素因数を $3$ つ以上持つような数について考える.(重複も含めて)素因数を $3$ つ持つ数のうち約数の個数が最小となるものは立方数であり,その個数は $4$ である.また,その次に約数の個数が小さいものは $p_{2}^{2} \cdot p_{2}$ ( $p_{1}, p_{2}$ は素数)の形で表されるもので,約数の個数は $6$ である.連続奇素数の和は偶数であるので,連続奇素数の和かつ立方数として有り得る数は $8$ のみである.　ここで, $p \geq 3$ とする.この時, $(左辺) \geq 2 + 4 + 6 + 6 = 18$ であるから $p$ として確認すべきものは $2$ のみである.実際, $p = 2$ の時等号が成立する.

MMPs013/★★☆☆☆

三角形 $A B C$ の外心を $O$ とする. $O A, O B, O C$ を直径とする円をそれぞれ $ω_{1}, ω_{2}, ω_{3}$ とし, $O B C, O C A, O A B$ の外接円をそれぞれ $Γ_{1}, Γ_{2}, Γ_{3}$ とする. $ω_{1}$ と $Γ_{1}$ の交点を $P_{1}$ とし,同様に $P_{2}, P_{3}$ についても定めた時, $O, P_{1}, P_{2}, P_{3}$ は同一円周上に存在することを示せ.

$A B C$ の外接円での反転を考える. $X$ を反転したものを $X^{'}$ と表現する.このとき,示すべきことは $P_{1}^{'}, P_{2}^{'}, P_{3}^{'}$ の共線である.　 $Γ_{1}, Γ_{2}, Γ_{3}$ はそれぞれ反転によって $B C, C A, A B$ に移る. $ω_{1}, ω_{2}, ω_{3}$ はそれぞれ反転によって $A, B, C$ に関する外接円の接線へと移る. $ω_{1}, ω_{2}$ の交点の反転先を $M_{1}$ などとすれば, $M_{1} C, M_{2} A, M_{3} B$ は全て内心を通る.したがって. $P_{1}^{'}, P_{2}^{'}, P_{3}^{'}$ はデザルグの定理より,共線である.

MMPs014/★☆☆☆☆

正整数に対して定義され,非負整数値をとる関数 $f$ であって,任意の正整数 $x$ に対して以下を満たすものを全て求めよ.
$f (x + 1) = f (f (x) + 1) + f (x)$

$f (x + 1) - f (x) = f (f (x) + 1) \geq 0$ より $f$ は広義単調増加関数である. $f (1) \geq 1$ と仮定する. $f (2) - f (1) = f (f (1) + 1) \geq f (2)$ より, $f (1) \leq 0$ を得るので矛盾する.よって, $f (1) = 0$ である.ここで, $f (k) = 0$ と仮定したときに $f (k + 1) = f (f (k) + 1) + f (k) = f (1) = 0$ となるので帰納的に $f (x) = 0 \forall_{x} \in Z^{+}$ を得る.

MMPs015/★☆☆☆☆

実数に対して定義され実数値をとる関数 $f$ であって、任意の実数 $x, y$ に対して以下が成り立つようなものを全て求めよ.

$f (f (x) + y) = x + f (f (y))$

$(x, y) = (x, 0)$ より, $f (f (x)) = x$ であるから $f$ は全射である. $f (c) = 0$ なる実数 $c$ をとり, $(x, y) = (c, x)$ とすると $f (x) = c + x$ となる.逆に, $f (x) = x + c$ ( $c$ は任意の定数)とすれば与式を満たすことから $f (x) = x + c$ が解である.

MMPs016/★★☆☆☆

${a_{n}}$ を以下で定まる数列とする.任意の正整数 $k$ ,素数 $p$ に対して $a_{p} \cdot (k + 1)$ は $p$ の倍数であることを示せ.

$a_{1} = 0, a_{2} = k a_{n + 2} = (k - 1) a_{n + 1} + k a_{n}$

ここで,円を $p$ 個の扇型に区切り,隣り合う二つの扇型を同じ色で塗らないように,全体を $k + 1$ 色で塗り分ける方法の総数を考える.(ただし,回転して一致するものは同じものとして数える.)

扇型を $X_{1}$ ~ $X_{k + 1}$ と時計回りに名前をつける.この時, $X_{1}$ に色 $A$ を塗ったとして, $X_{n}$ に色 $A$ 以外のを塗る方法の総数を $a_{n}$ とすると $a_{n + 2} = (k - 1) a_{n + 1} + k a_{n}, a_{1} = 0, a_{2} = k$ を得る.ここで,求めるものは $\frac{(k + 1) a_{p}}{p}$ と表され,これは整数なので題意は示された.

MMPs017/★☆☆☆☆

$f (x)$ を以下のように定める.このとき, $f (p + 6)$ が $p$ の倍数となるような素数 $p$ を全て求めよ.

$f (x) = \sum_{i = 0}^{x - 1}_{x} p_{i}$

条件より, $f (x + 1) = (x + 1) f (x) + 1$ を得る. $f (p) = p a_{p - 1} + 1 \equiv 1 (\mod p)$ である.漸化式より, $f (p + 1) = (p + 1) f (p) + 1 \equiv 2 (\mod p)$ を得る.同様にして計算していくことにより, $f (p + 6) \equiv 1957 (\mod p)$ を得るので $1957$ は $p$ の倍数であることがわかる. $1957 = 19 \cdot 103$ であることより, $p = 19, 103$ である.

MMPs018/★★☆☆☆

${a_{n}}$ を $a_{1} = 1, a_{n + 1} = n a_{n} + 1$ で定まる数列とする.任意の正整数 $x, y$ に対して以下の式が整数となることを示せ.( $x \neq y$ )

$\frac{a_{x} - a_{y}}{x - y}$

帰納法を用いて $a_{n} = \sum_{i = 0}^{n - 1} \frac{(n - 1)!}{i!}$ であることを示す.(ここでは便宜上 $0! = 1$ とする.)

(i) $n = 1$ のとき, $a_{1} = 1 = \frac{0!}{0!}$ である.

(ii)　 $n = k$ のとき, $n = k + 1$ において
$\begin{aligned} a_{k + 1} & = k \sum_{i = 0}^{k - 1} \frac{(k - 1)!}{i!} + 1 \\ = \sum_{i = 0}^{k - 1} \frac{k!}{i!} + \frac{k!}{k!} \\ = \sum_{i = 0}^{k} \frac{k!}{i!} \end{aligned}$
よって, $a_{n} = \sum_{i = 0}^{n - 1} \frac{(n - 1)!}{i!}$ である.今, $a_{n + m} \equiv a_{n} (\mod m)$ を示せば良い.

$\begin{aligned} a_{n + m} & = (n + m - 1) \times (m + n - 2) \times \dots \times 2 \times 1 + (n + m - 1) \times (n + m - 2) \times \dots \times 2 + \dots + (n + m - 1) \end{aligned}$

$\begin{array}{r} a_{n} = (n - 1) \times (n - 2) \times \dots \times 2 \times 1 + (n - 1) \times (n - 2) \times \dots \times 2 + \dots + (n - 1) \end{array}$
$k$ 連続整数の積が $k$ の倍数であることに留意すれば以下が成り立つ.

$\begin{aligned} a_{n + m} & = (n + m - 1) \times (n + m - 2) \times \dots \times (n + 1) + (n + m - 1) \times (n + m - 2) \times \dots \times (n + 2) + \dots + (n + m - 1) \\ \equiv (n - 1) \times (n - 2) \times \dots \times 1 + (n - 1) \times (n - 2) \times \dots \times 2 + \dots + (n - 1) (\mod m) \\ = a_{n} \end{aligned}$
(これは $m \leq n$ の場合は明らかであるが, $m > n$ の場合もうまく消えるので各自で確認してみてほしい.)

MMPs019/★☆☆☆☆

任意の正整数 $n, m$ に対して以下が成り立つことを示せ.
$\begin{aligned} \sum_{i = 1}^{n}_{n} C_{i} \cdot m^{n - i} \cdot {(- 1)}^{i + 1} & = m^{n} - (m - 1)^{n} \end{aligned}$

$m a x (a_{1}, a_{2}, \dots, a_{n}) = m$ なる正整数の組は $m^{n} - (m - 1)^{n}$ 通り(右辺)である.また,包除原理を用いると左辺の表示も得られるので題意は示された.

MMPs020/★☆☆☆☆

$| A C | > | A B |$ , $∠ A = 60 °$ なる不等辺三角形 $A B C$ において,その外接円を $Ω$ とし, $Ω$ と $B C$ の垂直二等分線の交点のうち, $A$ を含む側の交点を $D$ とする. $A D$ の垂直二等分線と $A C$ の交点を $E$ とするとき, $| A B | = | C E |$ となることを示せ.