JMO2023問題だけ

　$5×5$のマス目に，図のような$4$マスからなるタイル何枚かをマス目に沿って置く．ここで，タイルは$\textbf{重ねて置いても良い}$が，マス目からはみ出してはならない．どのマスについても，そのマスを覆うタイルが$0$個以上$2$個以下であるとき，少なくとも$1$枚のタイルで覆われているマスの個数としてありうる最大の値を求めよ．
　ただし，タイルを回転させたり裏返したりしてもよい．

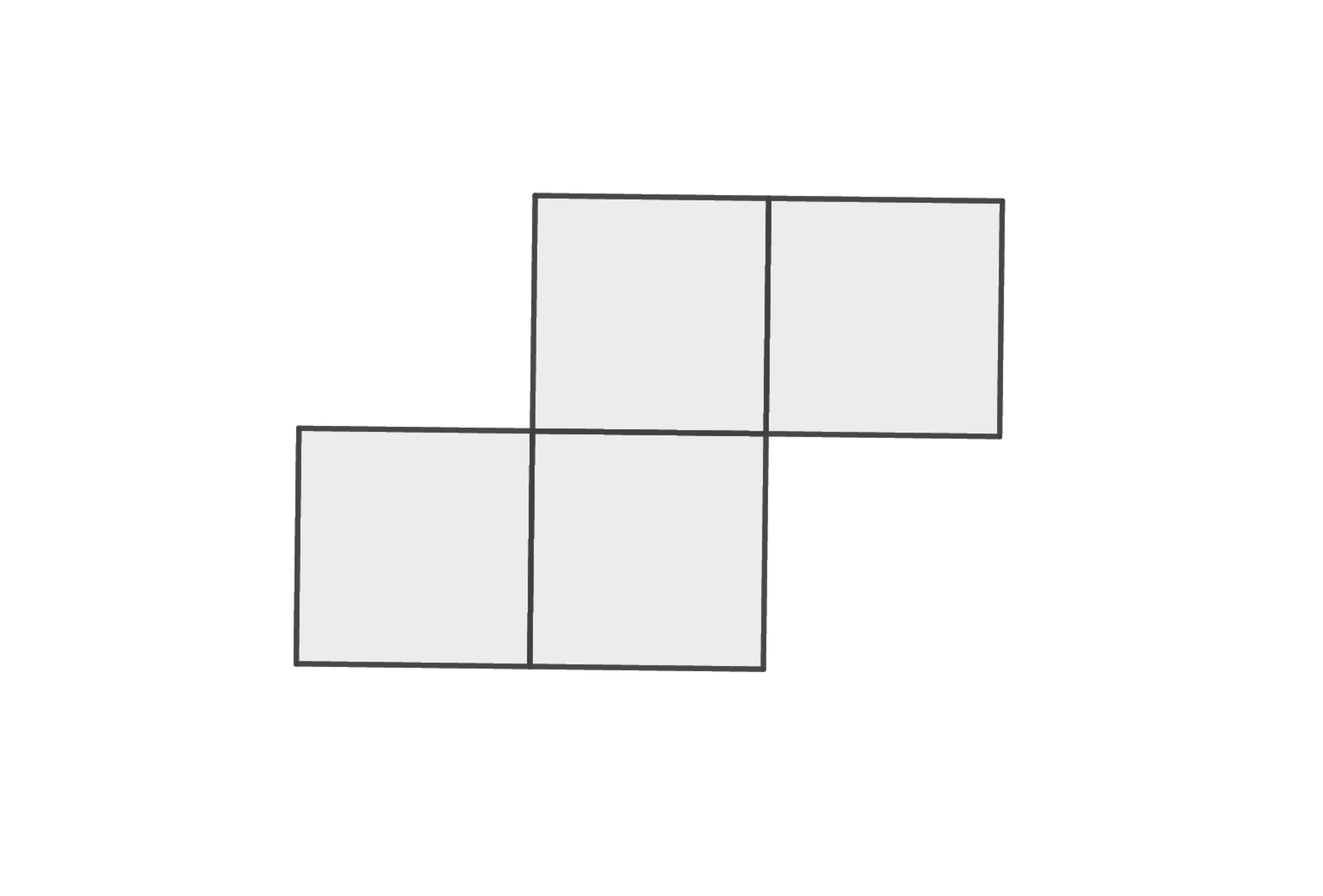図

　鋭角三角形$ABC$があり，辺$BC,CA,AB$の中点をそれぞれ$D,E,F$とし，$D$から辺$AB,AC$に下ろした垂線の足をそれぞれ$X,Y$とする．$F$を通り直線$XY$に平行な直線と直線$DY$が$E$と異なる点$P$で交わっている．このとき，直線$AD$と直線$EP$は垂直に交わることを示せ．

　$c$を非負整数とする．正の整数からなる数列$a_1,a_2,\ldots$であって，任意の正の整数$n$に対して次の条件をみたすものを全て求めよ．

　$a_i \geq a_{n+1}+c$をみたす正の整数$i$がちょうど$a_n$個存在する．

　正の整数$n$であって，$\dfrac{\phi(n)^{d(n)}+1}{n}$が整数であり，$\dfrac{n^{\phi(n)}-1}{d(n)^5}$が整数でないものをすべて求めよ．ただし，$n$と互いに素な$1$以上$n$以下の整数の個数を$\phi(n)$で表し，$n$の正の約数の個数を$d(n)$で表す．

　$S = \{1,2,\ldots,3000\}$とおく．このとき，次の条件を満たす整数$X$としてありうる最大の値を求めよ．

　任意の全単射$f:S→S$に対して，全単射$g:S→S$をうまくとることで，
$$\sum_{k=1}^{3000} \max\{f(f(k)),f(g(k)),g(f(k)),g(g(k))\}-\min\{f(f(k)),f(g(k)),g(f(k)),g(g(k))\}$$
を$X$以上にできる．