JMO2011-5の微分を使った解法
はじめに
JMO2023 お疲れ様でした
タイトルの通りです
本解を知らないのでただ自分の解法紹介になってるかもしれません。
前提知識は数III微分と数IIがいろいろ出てきます. 受験数学の知識で何とかなる気がします.
問題文
https://www.imojp.org/archive/challenge/old/jmo21mq.html
平面上に異なる4点があり, どの3点も同一直線上にないとする. このうち3点を頂点とする4つの三角形の内接円の半径の長さがすべて等しいならば, これら4つの三角形はすべて合同であることを示せ.
解法
まず自明考察（ここはすぐわかるので飛ばしても良い）
4点をA, B, C, Dとする. また共通の内接円半径を$r$とする.
4点ABCDは（適切に並び替えれば）凸四角形をなす
三角形ABCのなかに点Dが含まれるとき,
\begin{align}
\triangle{\mathrm{ABC}}&=\frac{r}{2}(\mathrm{AB+BC+CA})\\
&<\frac{r}{2}(\mathrm{AB+BD+DA})+\frac{r}{2}(\mathrm{BC+CD+DB})\\
&+\frac{r}{2}(\mathrm{CA+AD+DC})\\
&=\triangle{\mathrm{ABD}}+\triangle{\mathrm{BCD}}+\triangle{\mathrm{CDA}}=\triangle{\mathrm{ABC}}
\end{align}
となって矛盾する.
AC=BDが成立
\begin{equation}
\triangle{\mathrm{BCD}}+\triangle{\mathrm{ABD}}
=\triangle{\mathrm{ABC}}+\triangle{\mathrm{ADC}}
\end{equation}
および各三角形の内接円半径が等しいことから式変形すると導かれる.
本題
この後の議論として, AC=BD, AB=ABかつ$\triangle{\mathrm{ABD}}$と$\triangle{\mathrm{ABC}}$の内接円半径が等しいときにこの2三角形は合同であるかが気になります. すなわち, 長さが固定された二辺を動かした時, その二辺で張られる三角形の内接円半径はいつ等しくなるのかが気になるわけです.
そこで今回の本題です.
$a, b$を正実数とする.
長さが$a, b$である2つのベクトルで張られる三角形の内接円半径はなす角$\theta$を用いて$r(\theta)$と表される.
このときある$\theta_0\in(\frac{\pi}{3}, \frac{\pi}{2})$が存在して
\begin{equation}
r(\theta) \text{は}\begin{cases}
\mbox{単調増加} &(0<\theta<\theta_0) \\
\text{単調減少} & (\theta_0<\theta<\frac{\pi}{2})
\end{cases}
\end{equation}
が成立.
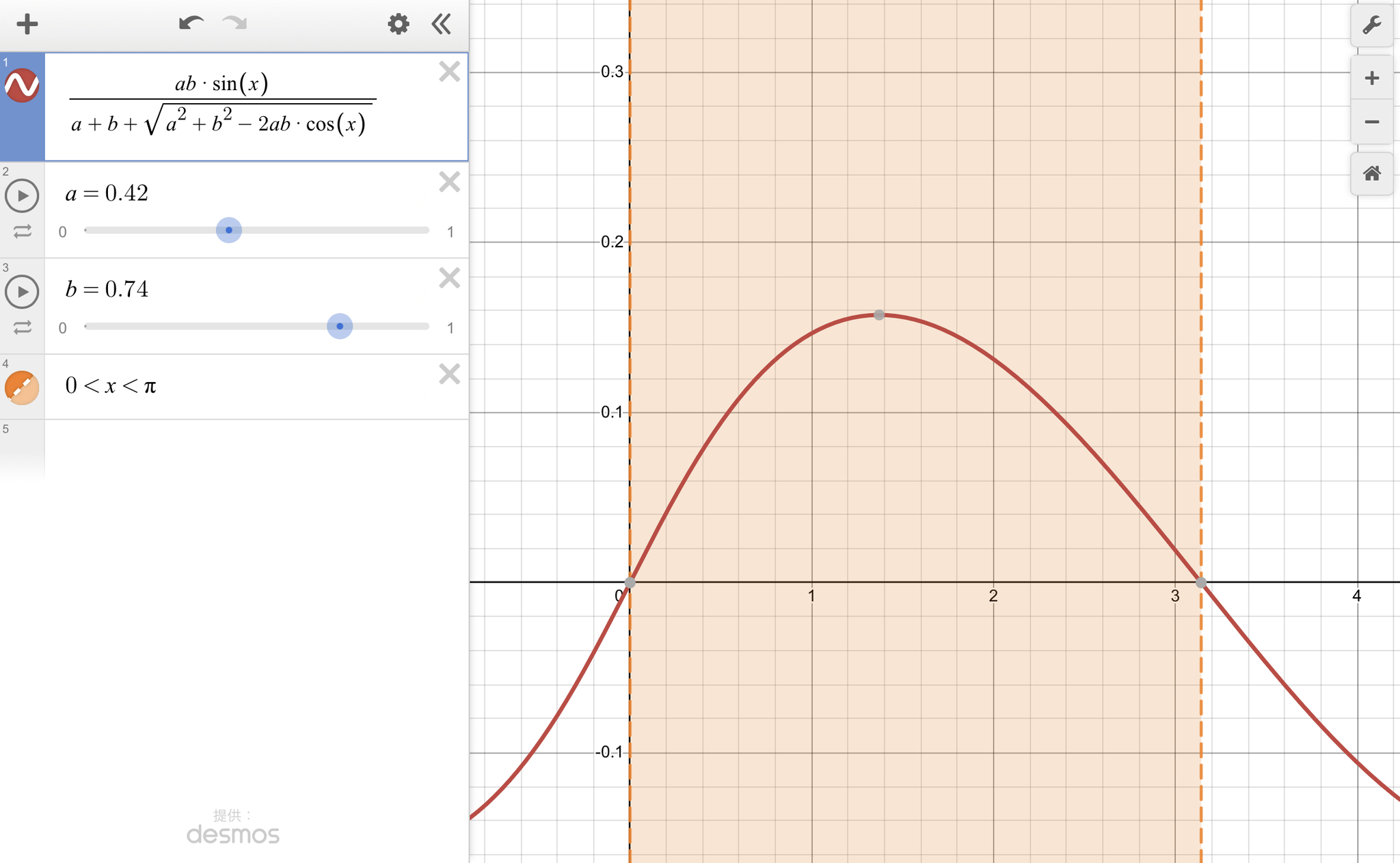グラフの概形
与えられた条件から$r(\theta)$は計算することができ,
\begin{equation}
r(\theta)=\frac{ab\sin{\theta}}{a+b+\sqrt{a^2+b^2-2ab\cos{\theta}}}
\end{equation}
と求まる.
微分して
\begin{equation}
r'(\theta)=
\frac{ab}{(a+b+\sqrt{a^2+b^2-2ab\cos{\theta}})^2}\{(a+b
+\sqrt{a^2+b^2-2ab\cos{\theta}})\cos{\theta}
-\frac{1}{2}\sin{\theta}
(a^2+b^2-2ab\cos{\theta})^{-\frac{1}{2}}
(2ab\sin{\theta})\}
\end{equation}
$t=\cos{\theta}$とおいて計算すると, $-1<\theta<1$のとき
\begin{equation}
r'(\theta)=0 \Leftrightarrow t^3+3t^2
-\frac{2a^2+ab+b^2}{ab}t+1=0
\end{equation}
$k=\frac{2a^2+ab+b^2}{ab}$とすることで, $t^3+3t^2-kt+1=0$を満たす解を求めることに帰着される.
いま$k\ge 5$なので, この三次方程式の解を考えると
\begin{equation}
0< t<\frac{1}{2}\Leftrightarrow \frac{\pi}{3}<\theta<\frac{\pi}{2}
\end{equation}
に一つのみ存在することがわかる. この値を$\theta_0$ とする.
あとは微分係数の正負をみれば示せる.
$r(\alpha)=r(\beta), \alpha\neq\beta$ならば$\alpha+\beta>90^\circ$
対称性より$\alpha<\beta$としてよい. $\alpha+\beta\le90^\circ$と仮定して矛盾を示す.
このとき$\alpha<\theta_0<\beta$を満たす. 特に$\beta>60^\circ$であり, 仮定より$\alpha<30^\circ. $
いま
\begin{equation}
r(\beta)=r(\alpha)< r(30^\circ)<\frac{ab}{2(a+b)}< r(90^\circ)
\end{equation}
より$\beta>\theta_0$における単調性から$\beta>90^\circ. $
これは仮定に矛盾.
解法（続き）
いま四角形ABCDは凸なので,
\begin{equation}
(\angle{\mathrm{BAC}}, \angle{\mathrm{ABD}}),
(\angle{\mathrm{CBD}}, \angle{\mathrm{BCA}}),
(\angle{\mathrm{DCA}}, \angle{\mathrm{CDB}}),
(\angle{\mathrm{ADB}}, \angle{\mathrm{DAC}})
\end{equation}
のすべての和は$360^\circ$であり, 上のいずれかの組はその和が$90^\circ$以下.
補題4を用いると, その組は二つの角度が等しいことが分かる.
ここでは$\angle{\mathrm{BAC}}= \angle{\mathrm{ABD}}$とする.
このとき$\triangle{\mathrm{ABC}}\equiv \angle{\mathrm{BAD}}$となり, 対称性から四角形ABCDは$\mathrm{AC}=\mathrm{BD}$なる等脚台形となる.
いま, 四角形ABCDの外接する円の半径を$R$とすれば
\begin{equation}
\triangle{\mathrm{ABC}}
=\frac{r}{2}(\mathrm{AB+BC+CA})
=\frac{\mathrm{AB\cdot BC\cdot CA}}{4R}
\end{equation}
\begin{equation}
\triangle{\mathrm{ADC}}
=\frac{r}{2}(\mathrm{AD+DC+CA})
=\frac{\mathrm{AD\cdot DC\cdot CA}}{4R}
\end{equation}
辺々割って
\begin{equation}
\frac{\mathrm{AB+BC+CA}}{\mathrm{AD+DC+CA}}
=\frac{\mathrm{AB\cdot BC\cdot CA}}{\mathrm{AD\cdot DC\cdot CA}}
\end{equation}
これに$\mathrm{BC=AD}$を用いると$\mathrm{AB=DC}$が導かれる.
四角形ABCDはAC=BDなる等脚台形であったから特に長方形となる.
このとき四つの三角形はすべて合同となり, 示される. $\blacksquare$
感想など
合同な組があるのを見つけるのが本質っぽくて, きっとうまい示し方があるんでしょうね. それでも命題3の結果は面白いなと感じました.
それにしてもJMO2011って割と簡単目なセットですね. まあもうJMO本選を受けることはないのでいまさら言っても仕方ありませんが。
この記事を高評価した人
この記事に送られたバッジ
投稿者
