2回合成関数が一次関数となる離散単調増加関数について

元になった問題をまず紹介しよう。

$\displaystyle \begin{array}{{>{\displaystyle}l}} 解法\\ 1< f( 1) < f( f( 1)) =3より、f( 1) =2,f( 2) =3\\ n\in \mathbb{N} について、f( k) =nとなるkが存在するとき、\\ f( n) =2a+1\\ よって、f( n+1) -f( n) =1のとき、m=f( n) として、\\ f( m+1) -f( m) =f( f( n+1)) -f( f( n)) =2\\ このとき、x=\frac{1}{2}( f( m+1) +f( m)) とすると、\\ f( m) < x< f( m+1) であり、f( f( m)) < f( x) < f( f( m+1))\\ つまり、2m+1< f( x) < 2m+3であり、f( x) =2m+2\\ 以上より、\Delta f( n) =f( n+1) -f( n) とすると、\\ \Delta f( n) は1がm個続くと、2がm個続き、1が2m個続き、2が2m個続き、\dotsc \\ を繰り返す数列になる。したがって、\\ f( 2024) =f( 1) +\sum _{n=1}^{2023} g( n) =2+1\times 1023+2\times 1000=3025\\ \\ この問題を解くだけでは面白くない。\\ 折角だしf_{1} の一般項の公式を入手しよう。詳しいことは後に回す\\ \\ f^{n}( 1) =A_{n} とする。\\ A_{0} =1\\ A_{1} =2\\ A_{n+2} =2A_{n} +1より、\\ A_{n+2} +1=2( A_{n} +1)\\ A_{2n} =2^{n+1} -1\\ A_{2n+1} =3\times 2^{n} -1\\ よって、\\ f\left( 2^{n+1} -1\right) =3\times 2^{n} -1\\ f\left( 3\times 2^{n} -1\right) =2^{n+2} -1\dotsc ①\\ この情報は今後も用いる。\\ f_{1}( n) =2,3,5,6,7,9,11,12,13,14,15,17,19,21,23,24,25\dotsc \\ f_{1}( n) =1,1,2,2,2,3,4,4,4,4,4\\ \Delta f_{1}( n) =f_{1}( n+1) -f_{1}( n) =1,2,1,1,2,2,1,1,1,1,2,2,2,2\\ \uparrow 1,2のどちらかしか出現しない\\ [ 証明]\\ fの出力には任意のnで2n+cが出現するから。\\ \rightarrow cが奇数なら2+c以上の全ての奇数、cが偶数なら2+c以上の全ての偶数が出現\\ \rightarrow 間隔は高々2\\ \\ A=\lfloor log_{2}( n+1)\rfloor \\ B=\left\lfloor log_{2}\left(\frac{n+1}{3}\right)\right\rfloor \\ として、\\ A-B=2\Leftrightarrow 2^{A} -1\leq n< 3\times 2^{A-1} -1\Leftrightarrow \Delta f_{1}( n) =1\\ A-B=1\Leftrightarrow 3\times 2^{A-1} -1\leq n< 2^{A+1} -1\Leftrightarrow \Delta f_{1}( n) =2\dotsc ②\\ ①、②より、\\ f_{1}( n) =\begin{cases} 2^{A-1} +n & \mathrm{if} \ \ 2^{A} -1\leq n< 3\times 2^{A-1} -1\ \\ 2n+1-2^{A} & \mathrm{if} \ 3\times 2^{A-1} -1\leq n< 2^{A+1} -1 \end{cases}\\ したがって、\\ f_{1}( n) =( A-B-1)\left( 2^{A-1} +n\right) -( A-B-2)\left( 2n+1-2^{A}\right)\\ =\left(\lfloor log_{2}( n+1)\rfloor -\left\lfloor log_{2}\left(\frac{n+1}{3}\right)\right\rfloor -1\right)\left( 2^{\lfloor log_{2}( n+1)\rfloor -1} +n\right) -\left(\lfloor log_{2}( n+1)\rfloor -\left\lfloor log_{2}\left(\frac{n+1}{3}\right)\right\rfloor -2\right)\left( 2n+1-2^{\lfloor log_{2}( n+1)\rfloor }\right)\\ \\ \end{array}$
この式にn=2024を代入して得たものが答えである。ちなみに、\
これをもとに2024までpythonで計算すると、
f(n)=2, 3, 5, 6, 7, 9, 11, 12, 13, 14, 15, 17, 19, 21, 23, 24, 25, 26, 27, 28, 29, 30, 31,
33, 35, 37, 39, 41, 43, 45, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62,
63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 96, 97, 98, 99, 100,
101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117,
118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 129, 131, 133, 135…,3025,…
複雑な形をしているが、それは重要ではない。この手の問題において一般項を求めるのは数学的には重要ではないと考えている。任意の項を計算で算出できることを視覚的に示すのが重要である。当然、この式よりもシンプルな式で表すのは可能かもしれない。

これを一般のf( x) =bx+c( b+c=3) に拡張するのは読者への挑戦状とする。考え方はこれまでと同じだ。
★実際にb,cに対応する解fの様子を計算するpythonソースコード\
https://github.com/Youteru/Functions-For-Which-the-Second-Composition-Becomes-A-Linear-Function
$\displaystyle \begin{array}{{>{\displaystyle}l}} f\left( f\left( x\right)\right) =2x+2ならどうなるだろうか。\\ f\left( 1\right) =2\\ f\left( 2\right) =4\\ f\left( 4\right) =6\\ f\left( f\left( x\right)\right) =2x+3なら\\ f\left( 1\right) =3\\ f\left( f\left( x\right)\right) =2x+4なら\\ f\left( 1\right) =3\\ f\left( 3\right) =6\\ f\left( 2\right) は4,5どちらかであり、それぞれ一意に定まる\\ f\left( f\left( x\right)\right) =2x+5なら\\ f\left( 1\right) =3,4\\ どちらも一意に定まる\\ f\left( f\left( x\right)\right) =2x+6なら\\ f\left( 1\right) =4\\ f\left( 4\right) =8\\ f\left( 2\right) ,f\left( 3\right) のあり得る値は5と6,5と7,6と7のどれか\\ 3通りある。\\ f\left( f\left( x\right)\right) =2x+7なら\\ f\left( 1\right) =4で3通り\\ f\left( 2\right) =5で1通り\\ f\left( f\left( x\right)\right) =2x+8なら\dotsc \\ \end{array}$

ここから本題に入ろう。ただただこの問題を一般化しよう。
fは単調増加関数で、f(f(x))=bx+cを満たすものとする。
各々の(b,c)に対応する解fの個数を表にまとめるとこうなる。
なぜこのような表になるのかっていう理由は省略する。
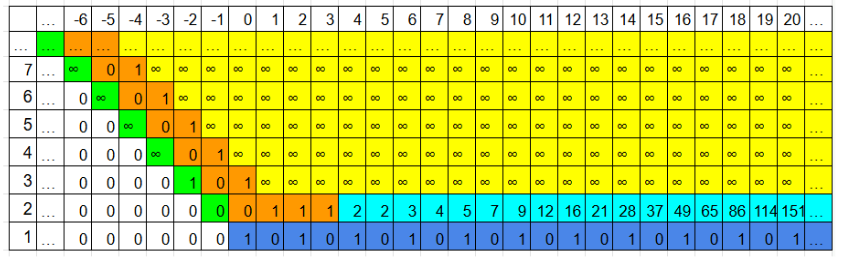(b,c)に対応するfの個数

$\displaystyle \begin{array}{{>{\displaystyle}l}} この公式のいい所は、cを負にも拡張されていることにある。\\ b >2のとき、fの解の個数は\\ b+c\leqq 0\Rightarrow 解0個\\ \left( f\left( f\left( 1\right)\right) が0以下になる\right)\\ b+c=1\Rightarrow b`=b,c`=0の\left( b`,c`\right) と同じ\\ \left( 理由はポスター参照\right)\\ b+c=2\Rightarrow 解0個\\ \left( f\left( f\left( 1\right)\right) =2より1< f\left( 1\right) < 2で、解なし\right)\\ b+c=3\Rightarrow 解1個\\ \left( f\left( f\left( 1\right)\right) =3より1< f\left( 1\right) < 3,f\left( 1\right) =2\right)\\ b+c\geqq 4\Rightarrow 解無限個\\ b >3のとき、解が2個以上存在するならば、無限個存在する。\\ \left( 理由はポスター参照\right)\\ \\ これによって、f\left( f\left( x\right)\right) が与えられたときに、条件を満たすfが存在するか否か、\\ 1個か2個以上かを瞬時に判定できるようになった。\\ \\ ここで、解fがいくつ存在するかは重要な問題である。\\ f_{1} ,f_{2} ,f_{3} は解は1つだけ\\ \left( b,c\right) =\left( 2,4\right) のとき解は2個、\left( b,c\right) =\left( 3,0\right) で解は無限個ある。\\ さらなる宇野公式\\ f_{c}\left( f_{c}\left( x\right)\right) =2x+cとして、\\ f_{1}\left( n\right) =2,3,5,6,7,9,11,12,13,14,15\dotsc \\ f_{2}\left( n\right) =2,4,5,6,8,10,11,12,13,14\dotsc \\ f_{3}\left( n\right) =3,4,5,7,9,10,11,12,13,15\dotsc \\ なんか規則性が見えてくる。それもそのはず。\\ \\ \end{array}$

メモ
定期テストの保健って暇だよね。余った時間で数学の研究をしました。
後々、先生に「答案用紙の裏に数式を書くな」って言われた。

$\displaystyle \begin{array}{{>{\displaystyle}l}} f_{c} の個数は有限であるため、\\ このような考え方は全ての解について成立する。\\ f_{c} 、f_{d} の個数をC,Dとして、c< dならばC\leqq Dということも分かる。\\ \\ 話はそれるが、f_{2} ,f_{3} の一般項の公式も獲得しよう。\\ f_{2}\left( n\right) =\left(\left\lfloor log_{2}\left( n+2\right)\right\rfloor -\left\lfloor log_{2}\left(\frac{n+2}{3}\right)\right\rfloor -1\right)\left( 2^{\left\lfloor log_{2}\left( n+2\right)\right\rfloor -1} +n+1\right) -\left(\left\lfloor log_{2}\left( n+2\right)\right\rfloor -\left\lfloor log_{2}\left(\frac{n+2}{3}\right)\right\rfloor -2\right)\left( 2n+3-2^{\left\lfloor log_{2}\left( n+2\right)\right\rfloor }\right) -1\\ f_{3}\left( n\right) =\left(\left\lfloor log_{2}\left( n+3\right)\right\rfloor -\left\lfloor log_{2}\left(\frac{n+3}{3}\right)\right\rfloor -1\right)\left( 2^{\left\lfloor log_{2}\left( n+3\right)\right\rfloor -1} +n+2\right) -\left(\left\lfloor log_{2}\left( n+3\right)\right\rfloor -\left\lfloor log_{2}\left(\frac{n+3}{3}\right)\right\rfloor -2\right)\left( 2n+5-2^{\left\lfloor log_{2}\left( n+3\right)\right\rfloor }\right) -2\\ f_{4} は2通り存在するのだった。\\ 片方は、\\ f_{4}\left( n\right) =\left(\left\lfloor log_{2}\left( n+4\right)\right\rfloor -\left\lfloor log_{2}\left(\frac{n+4}{3}\right)\right\rfloor -1\right)\left( 2^{\left\lfloor log_{2}\left( n+4\right)\right\rfloor -1} +n+3\right) -\left(\left\lfloor log_{2}\left( n+4\right)\right\rfloor -\left\lfloor log_{2}\left(\frac{n+4}{3}\right)\right\rfloor -2\right)\left( 2n+7-2^{\left\lfloor log_{2}\left( n+4\right)\right\rfloor }\right) -3\\ だが、もう片方は読者への宿題とする。\\ \\ 次に、あり得るパターンに関する公式の獲得を考えよう。\\ 宇野関数を定義する。\\ f_{c} としてあり得る個数をU\left( c\right) と表し、これを宇野関数とする。\\ 前述よりこの関数は広義単調増加である。\\ U\left( 1\right) =U\left( 2\right) =U\left( 3\right) =1\\ U\left( 4\right) =U\left( 5\right) =2\\ U\left( 6\right) =3\\ U\left( 7\right) =4\\ U\left( 8\right) =5\\ 宇野関数の正体は何だろうか。\\ \\ aを\frac{c+4}{3} \leq a\leq \frac{c+3}{2} となる任意のaとして、\\ f\left( 1\right) =a\\ f\left( a\right) =2+c\\ ①\frac{c+3}{2} =a\\ f\left( 1\right) \sim f\left( a\right) は一意に定まる。よって一意に定まる。\\ \rightarrow 1通り\\ ②\frac{c+4}{3} =a\\ f\left( a\right) \sim f\left( 2+c\right) は一意に定まる。f\left( 1\right) \sim f\left( a\right) はいい感じの値にして、一意に定まる。\\ \rightarrow 1通り\\ ③\\ 前提として、\frac{c+4}{3} \leqq a\leqq \frac{c+3}{2} である。この中の任意のaについて、\\ f\left( a\right) \sim f\left( 2+c\right) の対応する値\left( 2+c\sim 2a+c\right) を決定すると、f\left( 1\right) \sim f\left( a\right) は\\ 一意に定まる。\left( 証明は補題②を参照\right) fの出力には2n+c\left( n=1,2\dotsc a\right)\\ が含まれるので、それ以外に何が出現するかを決定したらよい。\\ \\ これは、cと偶奇が異なるので、\frac{2a+c-\left( 2+c\right)}{2} =a-1個のボールから\\ \left(\left( 2+c\right) -a+1\right) -a=3+c-2a個を選ぶ\\ 組合せの総数と一致するので、_{a-1} C_{3+c-2a} 通り\\ \\ よって、\\ U\left( c\right) =\sum _{a=\left\lceil \frac{c+4}{3}\right\rceil }^{\left\lfloor \frac{c+3}{2}\right\rfloor } \ _{a-1} C_{3+c-2a} =\sum _{a=\left\lceil \frac{c+1}{3}\right\rceil }^{\left\lfloor \frac{c+1}{2}\right\rfloor } \ _{a} C_{1+c-2a}\\ という公式を得ることができる。コンビネーションの足し算\\ であることに着目して、パスカルの三角形を召喚しよう。 \end{array}$
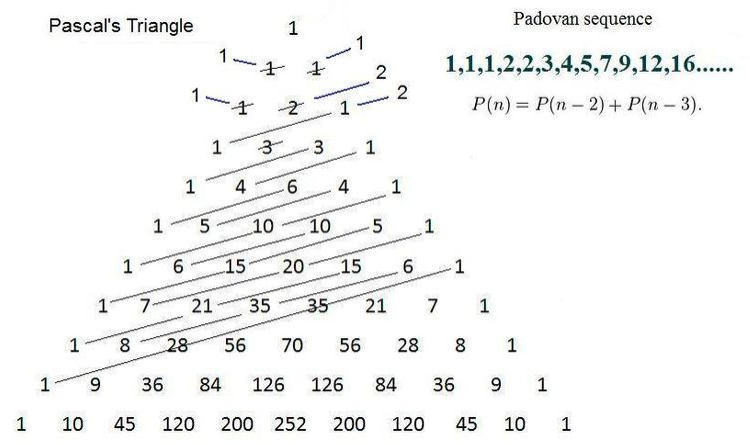パスカルの三角形
$\displaystyle \begin{array}{{>{\displaystyle}l}} 対応するコンビネーションがパスカルの三角形上で一直線に\\ 並んでいることが分かる。実はU\left( n\right) はパドヴァン数列と一致する。\\ 具体的には、P\left( 0\right) =P\left( 1\right) =P\left( 2\right) =1,\\ P\left( n\right) =P\left( n-2\right) +P\left( n-3\right) として、\left( n >2\right) U\left( n\right) =P\left( n-1\right) となる。\\ \\ \end{array}$

別の捉え方
長さnの直線グラフの極大独立集合の数はP(n-1)である。
これは階段を登るゆーてるくんを言い換えただけだ。

$\displaystyle \begin{array}{{>{\displaystyle}l}} ここまで来ると、今度はパドヴァン数列の一般項が気になる。\\ wolfram曰く、\\ x^{3} -x-1=0の解をp,q,rとして\\ 1の3乗根\upomega を用いて、\\ p=\sqrt[3]{\frac{1}{2} +\frac{\sqrt{69}}{18}} +\sqrt[3]{\frac{1}{2} -\frac{\sqrt{69}}{18}}\\ q=\upomega \sqrt[3]{\frac{1}{2} +\frac{\sqrt{69}}{18}} +\upomega ^{2}\sqrt[3]{\frac{1}{2} -\frac{\sqrt{69}}{18}}\\ r=\upomega ^{2}\sqrt[3]{\frac{1}{2} +\frac{\sqrt{69}}{18}} +\upomega \sqrt[3]{\frac{1}{2} -\frac{\sqrt{69}}{18}}\\ と表すことができる。\\ \left[ 証明\right] カルダノの公式に3次方程式の各係数を代入しなさい。\\ \\ P\left( n\right) =\frac{\left( q-1\right)\left( r-1\right) p^{n}}{\left( p-q\right)\left( p-r\right)} +\frac{\left( r-1\right)\left( p-1\right) q^{n}}{\left( q-r\right)\left( q-p\right)} +\frac{\left( p-1\right)\left( q-1\right) r^{n}}{\left( r-p\right)\left( r-q\right)}\\ \\ \left[ 証明\right] 行列の対角化を用いる\\ 出典　wolfram\ mathworld\\ \\ ここで|q|< 1,|r|< 1より、第二項、第三項は0に収束する。\\ これは、pがピゾ数であることに由来する。\\ よって,nが自然数のとき、\\ \\ P\left( n\right) =\left\lfloor \frac{\left( q-1\right)\left( r-1\right) p^{n}}{\left( p-q\right)\left( p-r\right)} +\frac{1}{2}\right\rfloor =\left\lfloor \frac{\left( p^{4} +1\right) p^{n}}{2p +3} +\frac{1}{2}\right\rfloor \\ =\left\lfloor \frac{\left(\sqrt[3]{\frac{1}{2} +\frac{\sqrt{69}}{18}} +\sqrt[3]{\frac{1}{2} -\frac{\sqrt{69}}{18}}\right)^{4} +1}{2\left(\sqrt[3]{\frac{1}{2} +\frac{\sqrt{69}}{18}} +\sqrt[3]{\frac{1}{2} -\frac{\sqrt{69}}{18}}\right) +3}\left(\sqrt[3]{\frac{1}{2} +\frac{\sqrt{69}}{18}} +\sqrt[3]{\frac{1}{2} -\frac{\sqrt{69}}{18}}\right)^{n} +\frac{1}{2}\right\rfloor \\ \\ ※式変形:a=\sqrt[3]{\frac{1}{2} +\frac{\sqrt{69}}{18}} ,b=\sqrt[3]{\frac{1}{2} -\frac{\sqrt{69}}{18}} として。\\ p=a+b\\ q=\upomega a+\upomega ^{2} b\\ r=\upomega ^{2} a+\upomega b\\ として代入してゴリ押し計算をしたら獲得できる。\\ \\ ※この公式は\sqrt[3]{\frac{1}{2} +\frac{\sqrt{69}}{18}} +\sqrt[3]{\frac{1}{2} -\frac{\sqrt{69}}{18}} の値が正確に分かっていないと使えないため、\\ 何らかのプログラミング言語で計算させる場合、\\ 行列の繰り返し2乗法を用いたほうが速い\\ 具体的には、\\ A=\begin{pmatrix} 0 & 1 & 0\\ 0 & 0 & 1\\ 1 & 1 & 0 \end{pmatrix} として、\\ A^{n} =\begin{pmatrix} P\left( n-5\right) & P\left( n-3\right) & P\left( n-4\right)\\ P\left( n-4\right) & P\left( n-2\right) & P\left( n-3\right)\\ P\left( n-3\right) & P\left( n-1\right) & P\left( n-2\right) \end{pmatrix}\\ となることを用いる\\ \left[ 証明\right] 難しくない。本筋ではないので省略する。\\ 出典　wolfram\ mathworld\\ \\ \\ \\ \bigstar パドヴァン数列を高速で計算するpythonソースコード\\ https://github.com/Youteru/Padovan-Sequence-with-Takahashi-s-Basics-in-Education-and-Learning\\ \\ 実際に\frac{\left( p^{4} +1\right) p^{n}}{2p +3} を計算させると、\\ n=1\rightarrow 0.9566111842910547\\ n=2\rightarrow 1.2672400139315272\\ n=3\rightarrow 1.6787356025941813\\ n=4\rightarrow 2.223851198222598\\ n=5\rightarrow 2.94597561652573\\ n=6\rightarrow 3.9025868008168083\\ n=7\rightarrow 5.169826814748367\\ n=8\rightarrow 6.84856241734259\\ n=9\rightarrow 9.072413615565242\\ n=10\rightarrow 12.018389232091046\\ どれも、誤差が\pm 0.5以内に収まり、\left\lfloor \frac{\left( p^{4} +1\right) p^{n}}{2p+3} +\frac{1}{2}\right\rfloor で一般項が計算できていることが\\ 分かる。\\ 最終的に宇野関数の一般項を求めることに成功した。\\ ちなみにパドヴァン数列に登場する素数が無限個あるか否かは未解決問題である。\\ これはフィボナッチ数列、ペル数列、一般のリュカ数列、ペラン数列に関しても\\ 同様である。\\ \\ 次に気になるのはb=3のときだ。\\ f\left( f\left( x\right)\right) =3xのときは一意に定まる。\\ f\left( f\left( x\right)\right) =3x+1のときは無限個生まれてしまう。\\ これはなぜか\\ 差が3になると、その間に入る自然数は2個生まれてしまうからだ。\\ これが無限の分岐を生み出す。しかし、特定のnに対するf\left( n\right) のとりうる値は常に\\ 有限である。なぜならfは単調増加であり、aによってA_{m} は確定するからだ。\\ \\ 一般に表にまとめるとこうなる。\\ やはり、b=2\ が異彩を放っている。\\ \\ 追求\\ ①f\left( f\left( f\left( x\right)\right)\right) =bx+cも考えてみよう\\ b=1なら、cが3の倍数ならf\left( x\right) =x+c/3\\ そうでないなら解なし\\ b=2以降が興味深い\\ 試しに、f^{3}\left( x\right) =2x+2\\ として、\\ f\left( n\right) =2,3,4,6,7,8,9,10,12,14,15,16,17,18\dotsc と続く\\ 考え方は全く同じで、数字の間隔は、2+c以降は1,2しか現れない。\\ f^{n}\left( 1\right) =A_{n} としよう。\\ A_{1} =a\\ A_{2} =p\\ A_{3} =2+c\\ A_{4} =2a+2\\ A_{5} =2p+c\\ \dotsc と一意に定まる。\\ つまり、3回合成のときでも行う議論は殆ど変わらないことが判明するのだ。\\ b,c,a,pが確定していたらあり得るfの個数はコンビネーションで表すことができる。\\ しかし、b,cが与えられた状態であり得るfの個数を求めるのは2回合成のときよりも\\ 困難である。なぜならa,p両方が動くからだ。\\ 一般にm回合成のとき、動く変数A_{1} ,A_{2} ,\dotsc ,A_{m-1} はm-1個だ。\\ \\ いかなるm回合成全てに共通するのは、\\ b=1のときはcがmで割り切れるなら1個、\\ 割り切れないなら0個\\ b=2のときはあり得るfの個数が有限であり非常に興味深い\\ b\geqq 3のときはあり得るfの個数は0,1,\infty のいずれかである\\ \\ ②f\left( f\left( x\right)\right) =bx^{2} +cx+dも考えてみよう。\\ 実は、解は必ず0個か無限個である。みんなも考えてみよう。\\ \left( 傾きが2の一次関数っていうのがいかに美しいかがここで分かるだろう\right) \end{array}$