数学第3回演習類題

まえがき

自校での数学αの問題演習の類題です。同校の者は復習用にお使いください。 記事をPDFにして使うのがよいでしょう。掲示されている問題から下に進むと解答が見られます。

第3回 類題：

$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $
$ $

解答

第3回大問1 座標平面と接線

$\text{(1)}$ $C_1$ について、半径は$\text{AP}=\sqrt{1+t^2}$ より、$C_1: \left(x-1\right)^2+y^2=1+t^2$.

また、$l_1$ は点$\text{A}$を通り $\displaystyle \overrightarrow{\text{AP}}=\begin{pmatrix} 1 \\ t\end{pmatrix}$ に垂直であるから、$l_1:\left(x-2\right)+t\left(y-t\right)=0 $ $\therefore \;$ $l_1:x+ty=2+t^2$ $\quad$ ($\displaystyle l_1:y=-\frac{1}{t}x+\frac{2+t^2}{t}$ も可)

$l_1$ 式導出別解：
$l_1$ は $\text{A}$ における $C_1$ の接線より、
$l_1 : \left(2-1\right)\left(x-1\right)+ty=1+t^2$
$\therefore \;$ $x+ty=2+t^2$

また、円$C_1$ 上の点 $\text{A}$ を通り $l_1$ に垂直な直線$l_2$ は直線 $\text{PA}$ を通るから、 $l_2: y=t\left(x-1\right)$, したがって、$l_2:y=tx-t$

$ $

$\text{(2)}$ $C_2$ は原点を通るので、実数$a,b$ を用いて $C_2:y=ax^2+bx$ と表される。
$f(x)=ax^2+bx$ とおくと、$l_2$ は $\text{A}$ を通る$C_2$ の接線であるから、$f'(2)=t -①,\quad f(2)=t -②$
$①\cdots \; 4a+b=t ,\quad ②\cdots \; 4a+2b=t$ より $\displaystyle a=\frac{1}{4}t,b=0$ であるから、$\displaystyle f(x)=\frac{1}{4}tx^2$
したがって、$\displaystyle C_2:y=\frac{1}{4}tx^2$

$ $

$\text{(3)}$ $C_2$ は$y$軸を軸として原点を頂点とする下に凸の放物線。したがって$D_2$ は下図着色部。(境界含む)
※ 図の着色部全体を円$C_1$ は含む。
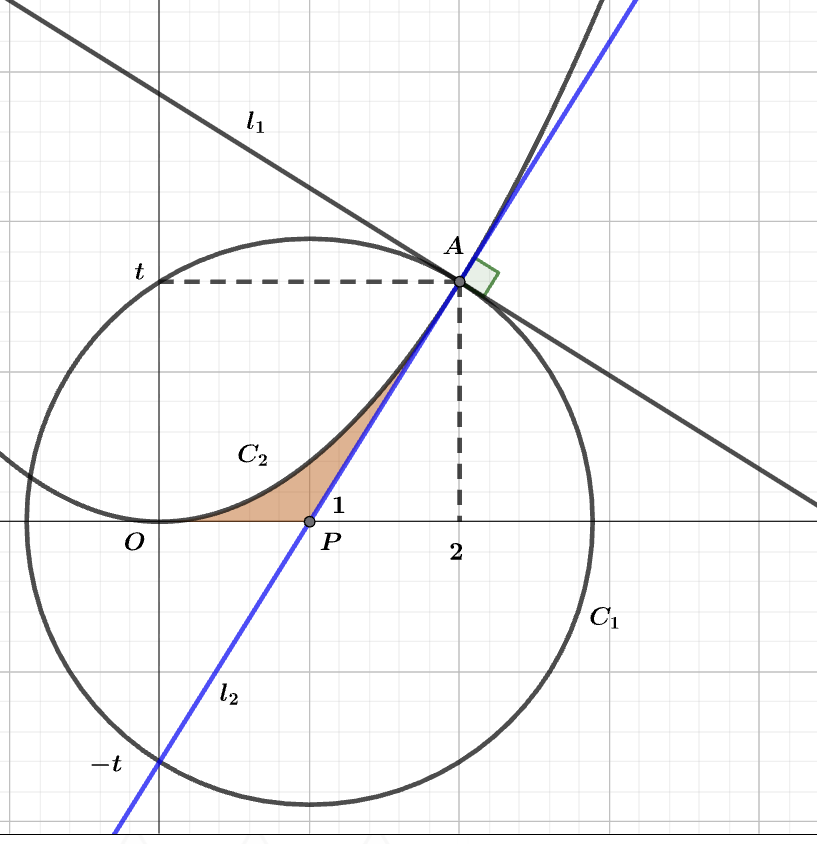図

$D_1$の面積：$π\left\{\sqrt{1+t^2}\right\}^2=π\left(1+t^2\right)$

$D_2$の面積：$\displaystyle \int_{0}^{2} \frac{1}{4}tx^2 dx-\frac{1}{2}\cdot 1\cdot t=\frac{1}{6}t$

したがって、$\displaystyle M=\frac{\left(D_2\text{の面積}\right)}{\left(D_1\text{の面積}\right)}$ とおくと、 $\displaystyle M=\frac{\frac{1}{6}t}{π\left(1+t^2\right)}=$$\displaystyle \frac{1}{6π}\cdot\frac{1}{t+\frac{1}{t}}$

$ $
$t>0$ より、$\displaystyle \frac{1}{t}>0$ であるから、相加相乗平均の関係より

$\displaystyle t+\frac{1}{t} \geq 2\sqrt{t\cdot \frac{1}{t}}=2$ $\quad$ (等号成立は $\displaystyle t=\frac{1}{t}$ すなわち $t=1$ のとき)

したがって、$\displaystyle M=\frac{1}{6π}\cdot\frac{1}{t+\frac{1}{t}}\leq \frac{1}{6π}\cdot \frac{1}{2}=\frac{1}{12π}$ で、等号成立は$t=1$ のとき。

以上から、$\displaystyle M=\frac{\left(D_2\text{の面積}\right)}{\left(D_1\text{の面積}\right)}$の最大値は $\displaystyle \frac{1}{12π} \;\left(t=1\right)$

第3回大問2 方程式と解の個数

$x^6-9x^4-12kx^3-9x^2+1=0 \quad -①$ とする。
$①$ は明らかに $x=0$ を解ににもたない。両辺を $x^3$ で割ると
$\displaystyle x^3-9x-12k-\frac{9}{x}+\frac{1}{x^3}=0 \quad -①'$

ここで、$\displaystyle t=x+\frac{1}{x}$ とおく。
$t$ と $x$ の値の対応を調べる。

また、$\displaystyle t=x+\frac{1}{x}$について、

$\displaystyle t^2-2=x^2+\frac{1}{x^2}$
\begin{aligned} x^3+\frac{1}{x^3} &=\left(x+\frac{1}{x}\right)\left(x^2-1+\frac{1}{x^2}\right) \\ &=t\left(t^2-3\right) \\ &=t^3-3t \end{aligned}
したがって、

$①'\cdots \quad \left(t^3-3t\right)-9t-12k=0$
$\qquad \qquad \displaystyle \frac{1}{12}t^3-t=k \quad -②$

$ $

$\displaystyle f(t)=\frac{1}{12}t^3-t$ とおいて、$②\cdots\quad f(t)=k\quad$ を満たす $t$ の値と個数について調べる。

以上から、

であるので、$①$の$x$の解の個数は
\begin{cases} \displaystyle k<-\frac{4}{3},\quad \frac{4}{3}< k \text{ のとき 2 個} \\ \displaystyle k=\pm \frac{4}{3} \text{ のとき 3 個} \\ \displaystyle -\frac{4}{3}< k<\frac{4}{3} \text{ のとき 4 個} \\ \end{cases} である。

第3回大問3 複素数平面

$\text{(1)}$ $K_1$ は $\displaystyle \frac{z}{z-2}$ が純虚数である$z$ の軌跡であるから、

$\displaystyle \frac{z}{z-2}=-\overline{\left(\frac{z}{z-2}\right)} \cdots -①$ として、

「$z$ が $K_1$ 上」 $\Leftrightarrow$ 「$z\neq 0,2$ かつ $①$」

$z\neq 0,2$ において
\begin{aligned} ①&\Leftrightarrow \frac{z}{z-2}+\frac{\overline{z}}{\overline{z}-2}=0 \\ \\ &\Leftrightarrow z\left(\overline{z}-2\right)+\overline{z}\left(z-2\right)=0 \\ \\ &\Leftrightarrow z\overline{z}-z-\overline{z}=0 \\ \\ &\Leftrightarrow \abs{z-1}^2=1 \\ \\ &\Leftrightarrow \abs{z-1}=1 \end{aligned}

したがって、$K_1$ は$2$点$0,2$ を除く円 $\abs{z-1}=1$
$K_1$

$ $

$\text{(2)}$ $\left(1-\sqrt{3}i\right)z+\left(1+\sqrt{3}i\right)\overline{z}=12 \quad -②$ について、整理すると

$\displaystyle ②\cdots \quad \frac{z+\overline{z}}{2}+\sqrt{3} \cdot \frac{z-\overline{z}}{2i}=6$

$z=x+iy \quad (x,y\in\mathbb{R})$ とおくと、$②\cdots\quad x+\sqrt{3}y=6$

したがって、実軸を$x$軸、虚軸を$y$軸とすると、$K_2$は直線$x+\sqrt{3}y=6$ を表す。
(複素平面上でいえば、実切片$6$,虚切片$2\sqrt{3}i$の直線を表す。)

$ $

$\text{(3)}$ 以降、 実軸を$x$軸、虚軸を$y$軸とする$xy$平面で考える。$K_1,K_2$ はそれぞれ　
$K_1: \left(x-1\right)^2+y^2=1 \quad \left(-1< x<1\right)$
$K_2: x+\sqrt{3}y=6$

で表される。$\displaystyle K_2: \frac{x}{6}+\frac{y}{2\sqrt{3}}=1$ であるから、$K_2$ は $x$切片$6$, $y$切片$2\sqrt{3}$ の直線である。

$xy$平面における$K_1$(黄色) , $K_2$(青色)

条件を満たす($\abs{\beta-\alpha}$が最小となる)のは図のときである。

したがって、$\displaystyle w-1=\frac{1+\sqrt{3}i}{2} \quad \therefore $ $\displaystyle w=\sqrt{3}\left(\cos{\frac{π}{6}}+i\sin{\frac{π}{6}}\right)$.

ここで、$w^{12}-1=\sqrt{3}^{12}\left(\cos 2π -\sin 2π\right)-1 \quad =728$ より、
\begin{aligned} \sum_{k=1}^{11}w^{k} &=-1+\sum_{k=1}^{12} w^{k-1} \\ \\ &= -1+ \frac{w^{12}-1}{w-1} \\ \\ &=-1+\frac{728}{\cos \frac{π}{3}+i\sin\frac{π}{3}} \\ \\ &=-1+728\left(\cos \frac{π}{3}-i\sin\frac{π}{3}\right) \\ \\ &=-1+728\cdot \frac{1-\sqrt{3}i}{2} \end{aligned}

$\quad$ $\quad =363-364\sqrt{3}i$

第3回大問4 区分求積法の収束速度

$\text{(1)}$ 区分求積法より
$\displaystyle \lim_{n\rightarrow ∞} a_n $ $ \displaystyle =\int_{0}^{1} \sin{x} \; dx$ $=\displaystyle \left[-\cos{x}\right]_{0}^{1}$ $\displaystyle =1-\cos{1}$

$ $

$\text{(2)}$ $xy$ 平面について、曲線 $C: y=\sin{x}$ を考える。また、$f(x)=\sin x$ を考える。
$0\leq x\leq 1$ において、 $f(x)=\sin{x}\geq 0, \quad$ $ f'(x)=\cos{x}>0, \quad f''(x)=-\sin{x}\leq 0$ であるから、曲線$C$ は$0 \leq x \leq 1$ で単調増加かつ上に凸

ここで、$1\leq k \leq n$ を満たす $k$ について、次のように点をとる。

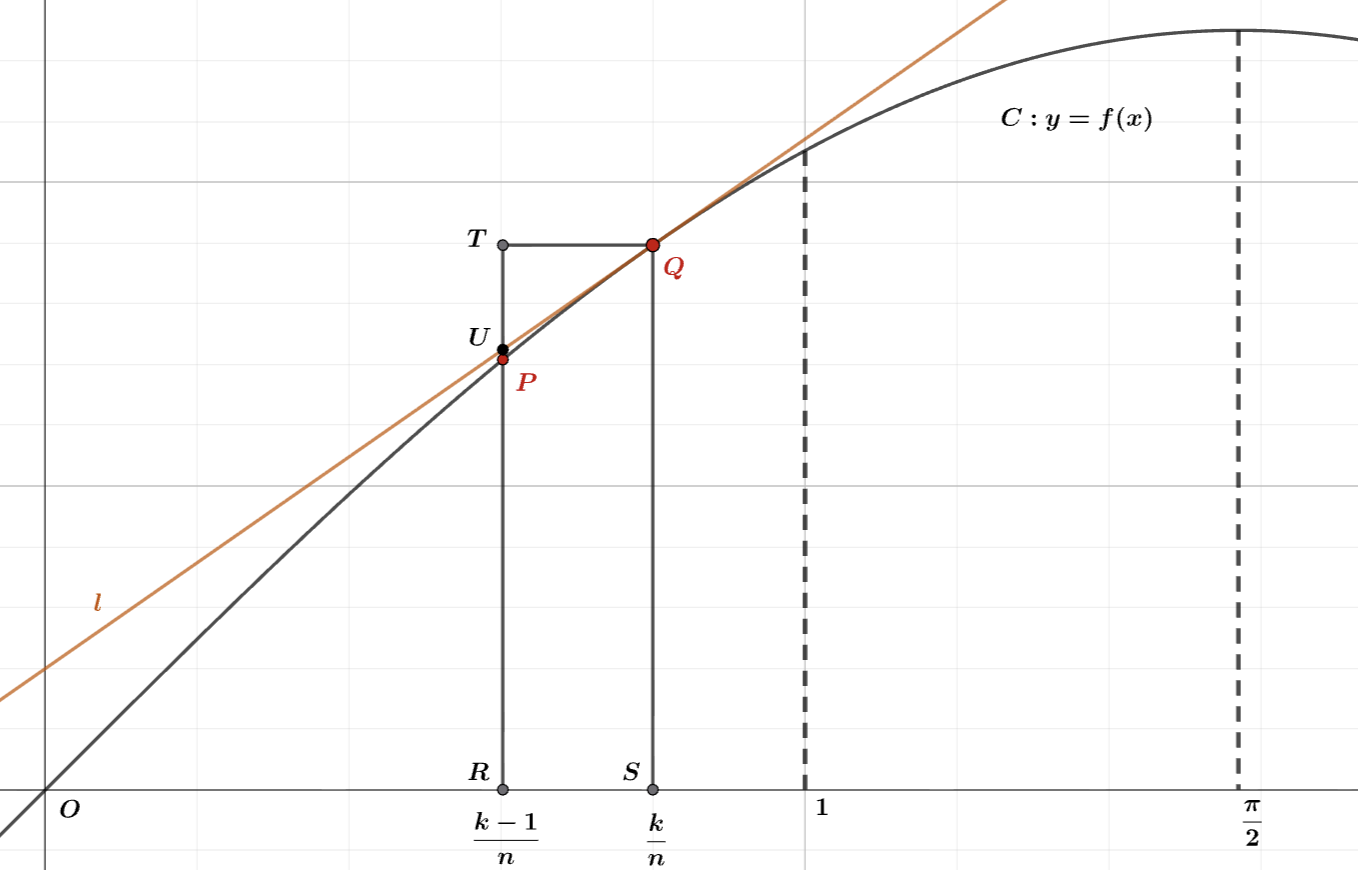図1

($\text{P},\text{Q}$ は $C$ 上の点で$x$座標がそれぞれ$\displaystyle \frac{k-1}{n} , \frac{k}{n}$であり、 $\text{PQ} \; // \; \text{QS} \; // \; y$軸, $\text{QT} \; // \; x$軸, $\text{T,P,R}$ は共線。)
$l$ を点$\text{Q}$ における$C$ の接線であり、$l$ と $\text{TR}$ の交点を $\text{U}$ とする。

下図の着色部$(*1)$ の領域の面積を$S_1$ とする。

$\displaystyle (*1) \cdots\quad \frac{k-1}{n} \leq x\leq \frac{k}{n}$ かつ $\displaystyle f(x)\leq y\leq f\left(\frac{k}{n}\right)$ の部分。

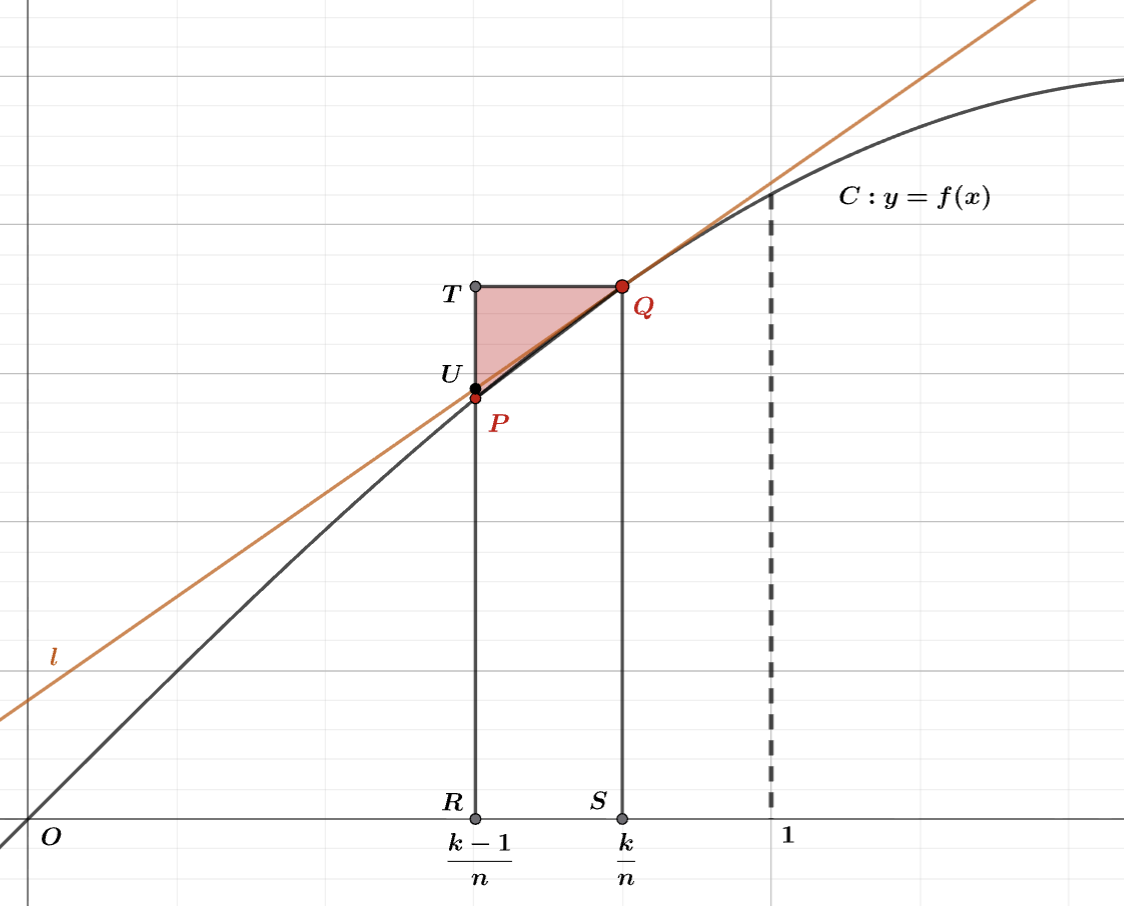図2

$0\leq x \leq 1$ で$f(x)$ は単調増加で $C$ が上に凸であるから、 $\triangle\text{TQU}< S_1<\triangle\text{TQP} \quad -①$

$S_1$ について：
$\displaystyle S_1=\frac{1}{n} f\left(\frac{k}{n}\right) \;- \int_{\frac{k-1}{n}}^{\frac{k}{n}} f(x) \;dx$

$ $

$\triangle\text{TQP}$ について：
・$\displaystyle \text{TQ}=\frac{1}{n}$
・$\displaystyle \text{TP}=f\left(\frac{k}{n}\right)-f\left(\frac{k-1}{n}\right)$

$\triangle\text{TQP}$ $\displaystyle =\frac{1}{2} \cdot \text{TQ} \cdot \text{TP} $

$\qquad$ $\; $ $\displaystyle =\frac{1}{2n}\left\{f\left(\frac{k}{n}\right)-f\left(\frac{k-1}{n}\right)\right\} $

$ $

$\triangle\text{TQU}$ について：
・$\displaystyle \text{TQ}=\frac{1}{n}$
・$l$ の傾きは $\displaystyle f'\left(\frac{k}{n}\right) \left(>0\right)$ であるから、$\displaystyle \text{TU}=\frac{1}{n}f'\left(\frac{k}{n}\right)$

$\triangle\text{TQU}$ $\displaystyle =\frac{1}{2} \cdot \text{TQ} \cdot \text{TU} $

$\qquad$ $\; $ $\displaystyle =\frac{1}{2n^2}f'\left(\frac{k}{n}\right)$

$ $

以上から、$\displaystyle ① \cdots \quad \frac{1}{2n^2}f'\left(\frac{k}{n}\right)\;\;<\frac{1}{n} f\left(\frac{k}{n}\right) \;- \int_{\frac{k-1}{n}}^{\frac{k}{n}} f(x) \;dx\;\;<\frac{1}{2n}\left\{f\left(\frac{k}{n}\right)-f\left(\frac{k-1}{n}\right)\right\}$

$f(x)=\sin{x}, \quad f'(x)=\cos{x}$ であるから、
$\displaystyle \frac{1}{2n^2}\;\cos\frac{k}{n} \; <\; \frac{1}{n} \; \sin \frac{k}{n} \;- \int_{\frac{k-1}{n}}^{\frac{k}{n}} \sin{x} \;dx \; <\; \frac{1}{2n} \left\{\sin\frac{k}{n}-\sin\frac{k-1}{n}\right\} \quad -(*)$

が導かれる。

$ $

$\text{(3)}$ $(*)$ は $k=1,2,3,\cdots,n$ で成り立つから、辺々を足して
$$\frac{1}{2n^2}\sum_{k=1}^{n}\cos\frac{k}{n} \; <\; \sum_{k=1}^{n}\left\{\frac{1}{n} \; \sin\frac{k}{n} \;- \int_{\frac{k-1}{n}}^{\frac{k}{n}} \sin{x} \;dx \right\} \; <\; \frac{1}{2n} \sum_{k=1}^{n}\left\{\sin\frac{k}{n}-\sin\frac{k-1}{n}\right\} $$
$$\frac{1}{2n^2}\sum_{k=1}^{n}\cos\frac{k}{n} \; <\; \frac{1}{n} \sum_{k=1}^{n} \sin\frac{k}{n} \;- \int_{0}^{1} \sin{x} \;dx \; <\; \frac{1}{2n} \; \sin 1 $$

ここで、 $\displaystyle \int_{0}^{1} \sin{x} \;dx \; =\lim_{n\rightarrow ∞} a_n=\alpha$ であるから、

$$\frac{1}{2n^2}\sum_{k=1}^{n}\cos\frac{k}{n} \; <\; a_n \;- \alpha \; <\; \frac{1}{2n} \; \sin 1 $$
両辺$n\;\left(>0\right)$ 倍して

$$\frac{1}{2n}\sum_{k=1}^{n}\cos\frac{k}{n} \; <\; n\left( a_n \;- \alpha \right)\; <\; \frac{1}{2} \; \sin 1 \quad -②$$

$ $

ここで、
\begin{aligned} \lim_{n\rightarrow ∞} \frac{1}{2n}\sum_{k=1}^{n}\cos\frac{k}{n} &= \frac{1}{2}\int_{0}^{1} \cos{x} \;dx \\ \\ &=\frac{1}{2}\left[\sin{x}\right]_{0}^{1} \\ \\ &=\frac{1}{2}\sin{1} \end{aligned}
$\displaystyle \lim_{n\rightarrow ∞} \frac{1}{2}\sin{1} \quad =\frac{1}{2}\sin{1}$

$ $
であるから、はさみうちの原理より

$②\cdots \quad$ $\displaystyle \lim_{n\rightarrow ∞} n\left(a_n-\alpha \right)=\frac{1}{2}\sin{1}$.