眠り姫問題：コイントスの結果に応じて実現する事象の確率について

　手前味噌で申し訳ありませんが、拙書『 こうして眠り姫問題は解決しましたとさ… 』の第３章では、眠り姫問題の質問「コイントスの結果が表だったということに対する、今のあなたの信用度は（確率で表せば）どのくらいですか？」の答を、主にベイズの定理を使って考えて、「それは1/2である」と結論しています。そして第４章では、眠り姫問題の実験中に行われるコイントスの結果に応じて実現する事象、つまり

　「今」は、コインが…
　　Hm：表だった時の月曜日である
　　Tm：裏だった時の月曜日である
　　Tt：裏だった時の火曜日である

これらの事象それぞれの、それが実現する確率を、これらの事象を標本点に持つ標本空間はどのようなものかを考えて、

　「事象Tmと事象Ttが互いに排反であると見做すならば、
　　P(Hm)=1/2, P(Tm)=P(Tt)=1/4 である」

と結論しています。
　本記事では、これらの、私が導き出した確率の値が正しいことを実験で確認します。

　上の実験中、起こされて質問された後、あなたは、コイントスの結果が表／裏か・今日は月曜日／火曜日か に応じて、それぞれ決められた色と枚数のチップを貰えるものとします。そして、貰ったチップは、あなたが再度眠りに就く前に、あなたの枕元にある箱に入れられるとします。
　それでは、

■ P(Hm)=1/2, P(Tm)=P(Tt)=1/4 と仮定して実験する

　P(Hm)=1/2, P(Tm)=P(Tt)=1/4 と仮定します。その上で、事象Hm, Tm, Ttそれぞれに対応する、その内側の面積が それに対応する事象が実現する確率の大きさに相当する「枠」を考えます。そして、これらの枠の中に図１のようにチップを置き（そうすると、全てのチップに同じ“価値”を持たせるならば、チップ１枚の“額”は確率1/4になります）、実験中に先の事象のいずれかが実現したら、その事象に対応する枠の中にあるチップを貰えるものとします。
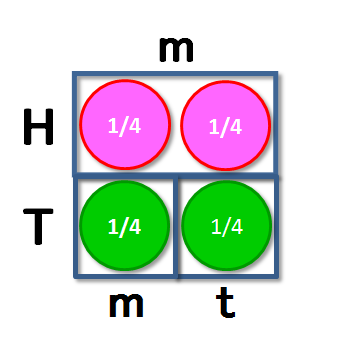私の答に基づいた、Hm, Tm, Ttの枠と その中に置かれたチップ
つまり、あなたがコイントスの結果が表だった場合の月曜日に起こされた（Hm）時にはピンク色のチップを２枚、コイントスの結果が裏だった場合の月曜日に起こされた（Tm）時には緑色のチップを１枚、そしてコイントスの結果が裏だった場合の火曜日に起こされた（Tt）時にも緑色のチップを１枚貰えます。
　とすれば、あなたが起こされて、「実験は終了しました」と知らされた「今」が「コイントスの結果が表だった場合」の水曜日であったなら、箱の中には（月曜日に貰った）ピンク色のチップが２枚有るはずです。このことは、コイントスが、事象Hm, Tm, Ttの内どれを実現させるか、すなわち、あなたを何度・何曜日に起こすかを決める唯一の試行であるので、「コイントスで表がでたら、あなたは（水曜日の起床時に）ピンク色のチップ２枚を得る」のと同じことです。チップ１枚の額は1/4でしたので、「コイントスで表がでた場合に あなたが得る」チップの総額は 1/4×2=1/2 であり、これは「コイントスで表がでる」確率1/2と一致します。
　一方、あなたが起こされて、「実験は終了しました」と知らされた「今」が「コイントスの結果が裏だった場合」の水曜日であったなら、箱の中には（月曜日と火曜日に１枚ずつ貰った）緑色のチップが２枚有るはずです。このことは、「コイントスで裏がでたら、あなたは（水曜日の起床時に）緑色のチップ２枚を得る」のと同じことです。チップ１枚の額は1/4でしたので、「コイントスで裏がでた場合に あなたが得る」チップの総額は 1/4×2=1/2 であり、これは「コイントスで裏がでる」確率1/2と一致します。
　以上のことは、初めの、事象Hm、Tm、Ttそれぞれに対応する枠の“大きさ”の設定が適正であったこと、つまり、P(Hm)=1/2, P(Tm)=P(Tt)=1/4 が正しいことの証左となります。
　では今度は、1/3派が主張するように、P(Hm)=P(Tm)=P(Tt)=1/3 だと仮定して実験したらどうでしょうか？

■ P(Hm)=P(Tm)=P(Tt)=1/3 と仮定して実験する

　P(Hm)=P(Tm)=P(Tt)=1/3 と仮定します。その上で、事象Hm, Tm, Ttそれぞれに対応する、その内側の面積が それに対応する事象が実現する確率の大きさに相当する「枠」を考えます。そして、これらの枠の中に図２のようにチップを置き（そうすると、全てのチップに同じ“価値”を持たせるならば、チップ１枚の“額”は確率1/3になります）、実験中に先の事象のいずれかが実現したら、その事象に対応する枠の中にあるチップを貰えるものとします。
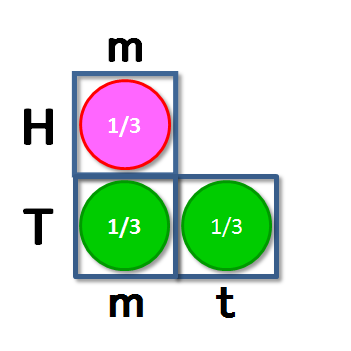1/3派の答に基づいた、Hm, Tm, Ttの枠と その中に置かれたチップ
　つまり、あなたがコイントスの結果が表だった場合の月曜日に起こされた（Hm）時にはピンク色のチップを１枚、コイントスの結果が裏だった場合の月曜日に起こされた（Tm）時には緑色のチップを１枚、そしてコイントスの結果が裏だった場合の火曜日に起こされた（Tt）時にも緑色のチップを１枚貰えます。
　とすれば、あなたが起こされて、「実験は終了しました」と知らされた「今」が「コイントスの結果が表だった場合」の水曜日であったなら、箱の中には（月曜日に貰った）ピンク色のチップが１枚有るはずです。このことは、「コイントスで表がでたら、あなたは（水曜日の起床時に）ピンク色のチップ１枚を得る」のと同じことです。チップ１枚の額は1/3でしたので、「コイントスで表がでた場合に あなたが得る」チップの総額は 1/3×1=1/3 であり、これは「コイントスで表がでる」確率1/2と一致しません。
　一方、あなたが起こされて、「実験は終了しました」と知らされた「今」が「コイントスの結果が裏だった場合」の水曜日であったなら、箱の中には（月曜日と火曜日に１枚ずつ貰った）緑色のチップが２枚有るはずです。このことは、「コイントスで裏がでたら、あなたは（水曜日の起床時に）緑色のチップ２枚を得る」のと同じことです。チップ１枚の額は1/3でしたので、「コイントスで裏がでた場合に あなたが得る」チップの総額は 1/3×2=2/3 であり、これは「コイントスで裏がでる」確率1/2と一致しません。
　以上のことは、初めの、事象Hm、Tm、Ttそれぞれに対応する枠の“大きさ”の設定が適正ではなかったこと、つまり、P(Hm)=P(Tm)=P(Tt)=1/3 が間違いであることの証左となります。

■ おしまいに

　以上で、私の答、P(Hm)=1/2, P(Tm)=P(Tt)=1/4 が正しいことが実験で確認できました。従って、眠り姫問題の本来の質問「コイントスの結果が表だったということに対する、今のあなたの信用度は（確率で表せば）どのくらいですか？」の答は、コイントスの結果が表だった場合に実現するのは事象Hmのみなので、P(Hm)と同じ1/2となります。
　ちなみに、私は、Adam Elga氏による次の論述は承知しています。

そして、この「論述」が間違っていることについても 拙書『 こうして眠り姫問題は解決しましたとさ… 』の第４章で論証しています。