自作置き場

平行四辺形$ABCD$において, 点$E,F$はそれぞれ線分$AB,DA$上の点であり, $AE=AF$を満たす. 直線$EF$と直線$AC$の交点を$G$とすると, $\angle AGE=80^{\circ}$であった. 線分$BC$上に$HA=HC$を満たす点$H$をとったとき, $\angle BAH$の大きさを求めよ.
なお, $\angle BAC>\angle CBA$とする.

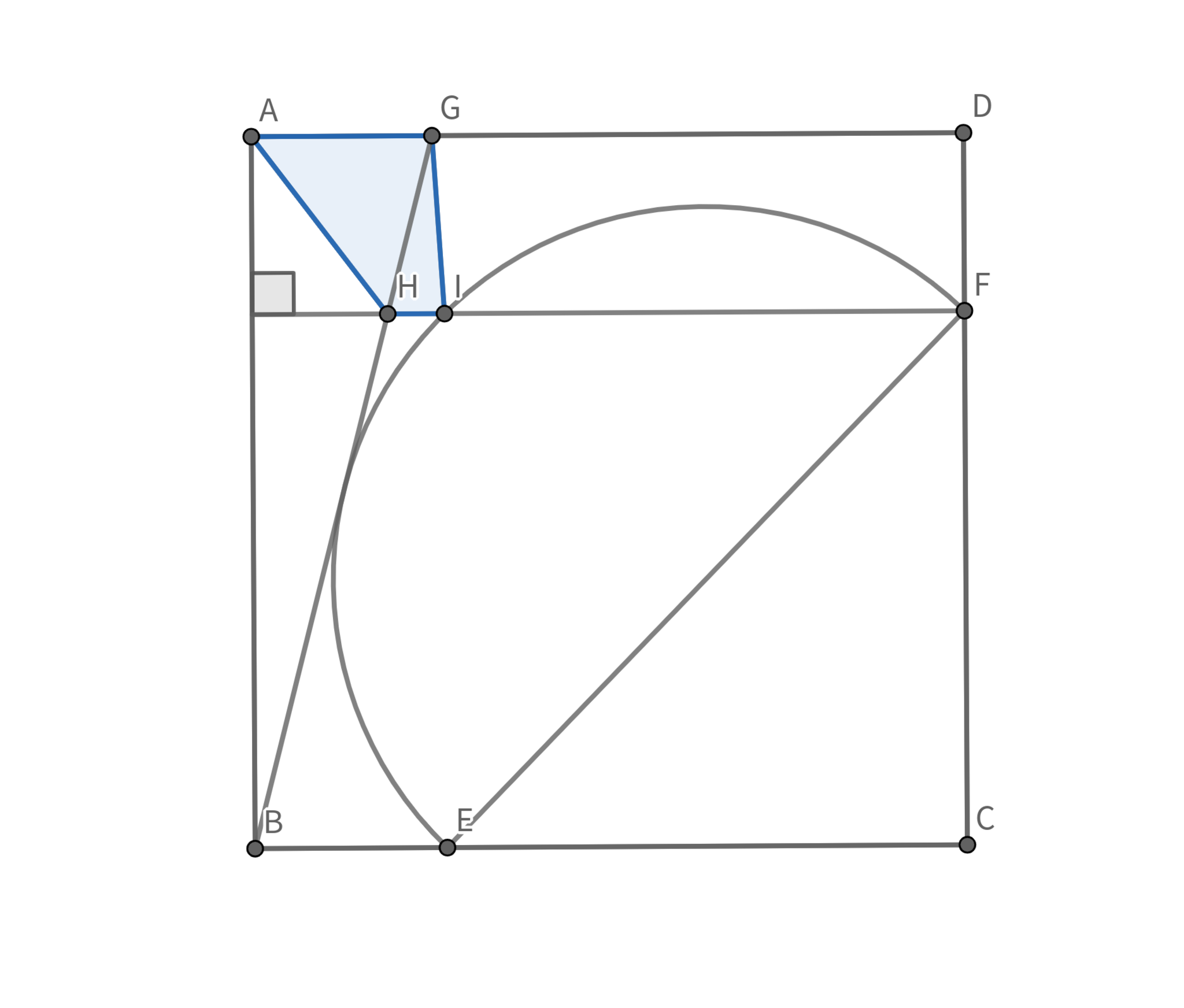
一辺の長さが$10$の正方形$ABCD$の内部に線分$EF$を直径とする半円$\Gamma$がある. なお, 点$E,F$はそれぞれ線分$BC, CD$上の点である.
点$B$から半円$\Gamma$に接線を引き, 直線$AD$との交点を点$G$とする.点$F$から直線$AB$へ垂線をおろし, 直線$BG$, 半円$\Gamma$との交点をそれぞれ点$H,I$とする.
$CF=\frac{15}{2}$, $\angle EFC+\angle AGB=120^{\circ}$であるとき,四角形$AHGI$の面積を求めよ.

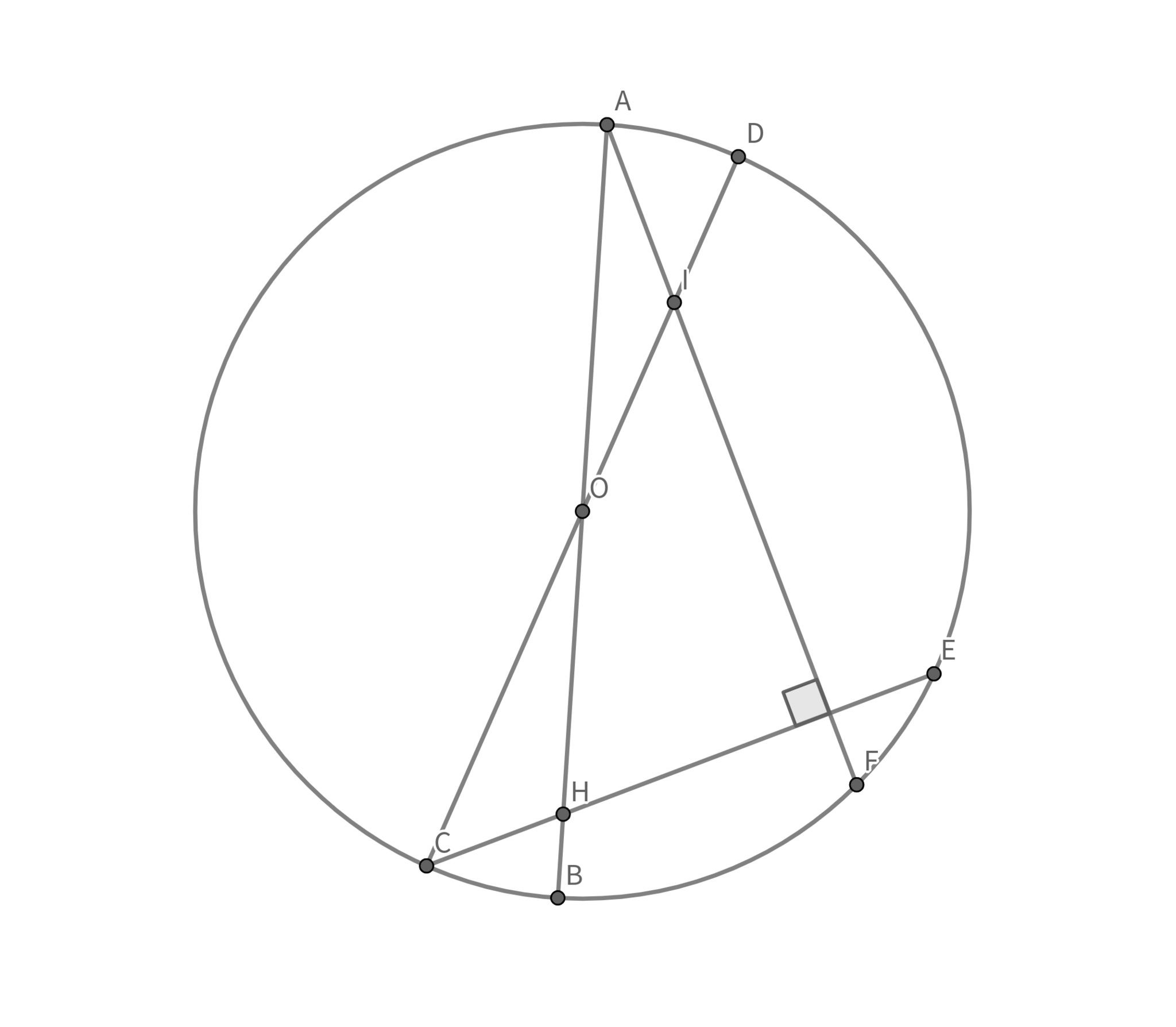
線分$AB$を直径とする円$\Gamma$上に互いに対蹠点となるような点$C,D$をとる.弧$ADB$上の点$E$に対し$CE\perp AF$となるような点$F(\neq A)$を円$\Gamma$上にとる. また, 直線$CE$と$AB,AF$と$CD$の交点を点$H,I$とする.
$CH:AI=4:3,BH:DI=2:3,AB=2$であるとき, 線分$DF$の長さを求めよ.

鈍角三角形$ABC$において, 点$C$から直線ABにおろした垂線の足を点$D$, 点$D$から直線$AC$におろした垂線の足を点$E$とする. また, 三角形$ABC$の外心を$O$とする.
三角形$ABC=10$, 三角形$OCE=6$であるとき, 三角形$BDC$の面積を求めよ.　

三角形$ABC$は$AB=AC$の二等辺三角形である. 線分$AC$上に点$D$をとり, 三角形$BCD$の外接円を$\Gamma$ , 線分$BC$の中点を$M$とする. 直線$AM$を直線$BD$関して対称移動させた直線と円$\Gamma$との交点をそれぞれ点$P,Q$としたとき, $∠PBA=∠DQA$であることを示せ. なお, 点$P$は直線$AM$で分割された領域のうち$B$を含む領域上の点で, 点$Q$は$C$を含む領域上の点である.

三角形$ABC$の外心を$O$, 三角形$OAB,OBC,OCA$の外心をそれぞれ$O_A,O_B,O_C$とする. 三角形$O_AO_BO_C$の外心は三角形$ABC$のオイラー線上にあることを示せ.

$O$を原点とする. $xy$平面上の点列$\{P_k\}_{k=1,2,3...}$を
\begin{align*} \overrightarrow{OP_k}\cdot\overrightarrow{P_kP_{k+1}}=0,\quad \overrightarrow{P_kP_{k+1}}\cdot\overrightarrow{P_{k+1}P_{k+2}}>0,\quad |\overrightarrow{P_kP_{k+1}}|=\frac{1}{k+1},\quad P_1=(1,0),\quad P_2=\Bigl(1,\frac{1}{2}\Bigl) \end{align*}
により定めるとき, 以下の命題(*)の真偽を答え, その証明をせよ.
なお, $\sum_{m=1}^{\infty}\frac{1}{m^2}$がある正の値に収束することは自由に用いて良い.
\begin{align*} \text{命題:点列 }\{P_k\}\text{はある点Pに収束する. }\cdots (*) \end{align*}

$m$を自然数として$f(x)$を$m$次のモニック多項式とする.
(1)任意の自然数$n$に対して$\sqrt[\huge m]{f(n)}$が有理数となるとき, $f(x)$は有理数$r$を用いて$f(x)=(x+r)^m$と表されることを示せ.
(2)任意の無理数$\omega$に対して$\sqrt[\huge m]{f(\omega)}$が無理数となるような$f(x)$は存在しないことを示せ.