定数係数線形漸化式の演算子的解法

演算子$S$の導入
定数係数同次線形漸化式の解法その１
隣接２項間漸化式$a_{n+1}=\lambda a_n+f(n)(\lambda\in\mathbb{C} \verb|\| \{0\})$の解
隣接３項間漸化式$a_{n+2}+pa_{n+1}+qa_n=0(p,q\in\mathbb{C})$の解
特殊解を使った非同次線形漸化式の解法
定数係数同次線形漸化式の解法その2
特性方程式が重解を持たない場合
特性方程式が重解を持つ場合

高校数学解説

定数係数線形漸化式の演算子的解法

漸化式,数列

416

読めばわかると思いますがこの記事は微分演算子を参考にして自分なりにまとめたものです。参考程度にお読みください。

演算子 $S$ の導入

$S a_{n} = a_{n + 1}$ や $S^{k} a_{n} = a_{n + k} (k = 0, 1, 2, \dots)$ となるように、演算子 $S$ を次のように定義します。

任意の数列 ${a_{n}}_{0, 1, 2, \dots}$ に対して、 $(C_{0} S^{k} + C_{1} S^{k - 1} + \dots + C_{k - 1} S + C_{k}) a_{n} = C_{0} a_{n + k} + C_{1} a_{n + k - 1} + \dots + C_{k - 1} a_{n + 1} + C_{k} a_{n}$ とする。ただし $C_{i} (i = 0, 1, \dots, k)$ は定数とする。

$a_{n + 1} - 2 a_{n} = (S - 2) a_{n}$
$a_{n + 2} + 2 a_{n + 1} + 3 a_{n} = (S^{2} + 2 S + 3) a_{n}$
$a_{n + 2} + a_{n + 1} = (S^{2} + S) a_{n} = (S + 1) a_{n + 1}$
$a_{n + k} - a_{n} = (S^{k} - 1) a_{n}$

$S$ の多項式に対して次の性質が成り立ちます。

基本性質

$f (S), g (S)$ を $S$ の複素係数多項式とする。
$𝟙 . f (S) (c a_{n}) = c f (S) a_{n}, f (S) (a_{n} + b_{n}) = f (S) a_{n} + f (S) b_{n}$
$𝟚 . f (S) + g (S) = g (S) + f (S), f (S) g (S) = g (S) f (S)$
$𝟛 . {f (S) \pm g (S)} a_{n} = f (S) a_{n} \pm g (S) a_{n}$
$𝟜 . f (S) {g (S) a_{n}} = {f (S) g (S)} a_{n}$ が成り立つ。

𝟙,𝟚,𝟛は省略。
𝟜は $\begin{array}{r} f (S) = \sum_{i = 0}^{k} C_{i} S^{i} (C_{i} \in C (i = 0, 1, \dots, k)) \end{array}$ として、 ${(S - λ) f (S)} a_{n} = (S - λ) {f (S) a_{n}} (λ \in C)$ を示せばよい。
$\begin{array}{rcl} {(S - λ) f (S)} a_{n} & = & {(S - λ) \sum_{i = 0}^{k} C_{i} S^{i}} a_{n} \\ = & (\sum_{i = 0}^{k} C_{i} S^{i + 1} - λ \sum_{i = 0}^{k} C_{i} S^{i}) a_{n} \\ = & \sum_{i = 0}^{k} C_{i} a_{n + i + 1} - λ \sum_{i = 0}^{k} C_{i} a_{n + i} \\ = & (S - λ) (\sum_{i = 0}^{k} C_{i} a_{n + i}) \\ = & (S - λ) {\sum_{i = 0}^{k} C_{i} S^{i} a_{n}} \\ = & (S - λ) {f (S) a_{n}} \end{array}$

$Δ = S - 1$ と定義すると数列 ${Δ a_{n}}$ は数列 ${a_{n}}$ の階差数列になります。

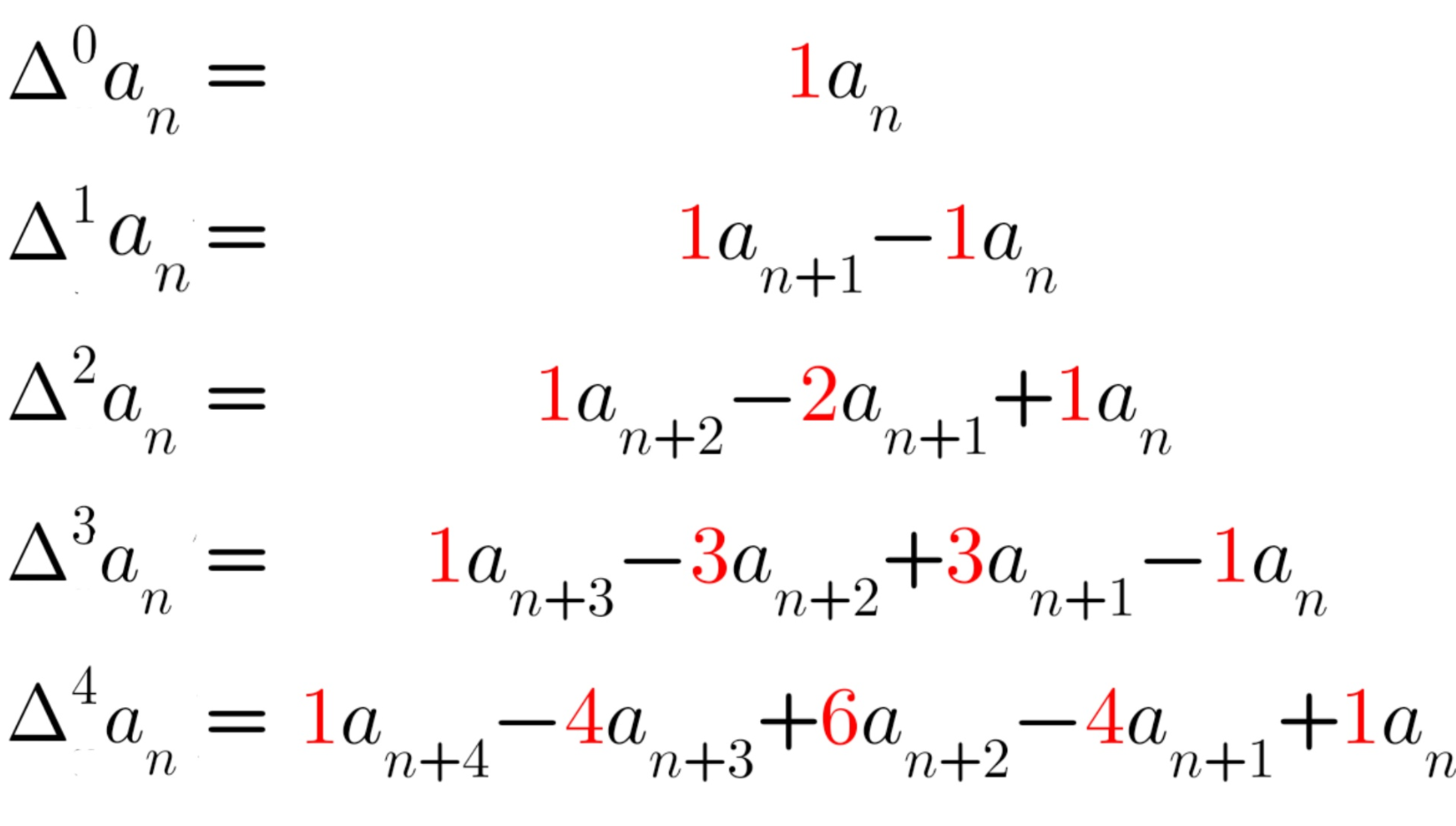パスカルの三角形

このように何回も階差を取り続けるとパスカルの三角形が現れますが、 $(S - 1)^{k}$ を展開してるだけと思えば当たり前です。

定数係数同次線形漸化式の解法その１

漸化式 $f (S) a_{n} = g (n)$ が与えられたとき、 $g (n) = 0$ なら同次漸化式、 $g (n) \neq 0$ なら非同次漸化式と呼ぶことにします。

ここで、 $f$ が $k$ 次の多項式ならこの漸化式を満たす数列 ${a_{n}}_{0, 1, 2, \dots}$ は $a_{i} (i = 0, 1, \dots, k - 1)$ を与えれば一意に定まるのでこれらが各々実数値を動くときの漸化式 $f (S) a_{n} = g (n)$ を満たす数列 ${a_{n}}_{0, 1, 2, \dots}$ 全体の集合を漸化式 $f (S) a_{n} = g (n)$ の解と呼ぶことにします。

そして、解が $\begin{array}{r} {h (n, C_{1}, C_{2}, \dots, C_{k}) | C_{i} \in C (i = 1, 2, \dots, k)} \end{array}$ であるとき、一般解は $a_{n} = h (n, C_{1}, C_{2}, \dots, C_{k})$ ( $C_{i} (i = 1, 2, \dots, k)$ は任意定数)であるともいうことにし、漸化式 $f (S) a_{n} = g (n)$ の解の要素を漸化式 $f (S) a_{n} = g (n)$ の特殊解と呼ぶことにします。

隣接２項間漸化式 $a_{n + 1} = λ a_{n} + f (n) (λ \in C \ {0})$ の解

$f (n) = 0$ のとき

$a_{n + 1} = λ a_{n}$ なので $a_{0} = C$ ( $C$ は任意定数)とすると、一般解は $a_{n} = C λ^{n}$ になります。

$λ = 1$ のとき

$a_{n + 1} = a_{n} + f (n)$ なので $a_{0} = C$ ( $C$ は任意定数)とすると、一般解は $a_{n} = C + \sum_{k = 0}^{n - 1} f (k) (n \geq 1)$ となります。

$a_{n + 1} = λ a_{n} + f (n)$ の解

$\begin{array}{rcl} a_{n + 1} & = & λ a_{n} + f (n) \\ \frac{a_{n + 1}}{λ^{n + 1}} & = & \frac{a_{n}}{λ^{n}} + \frac{f (n)}{λ^{n + 1}} \\ Δ \frac{a_{n}}{λ^{n}} & = & \frac{f (n)}{λ^{n + 1}} \\ \frac{a_{n}}{λ^{n}} & = & C + \sum_{k = 0}^{n - 1} \frac{f (k)}{λ^{k + 1}} \\ a_{n} & = & C λ^{n} + \sum_{k = 0}^{n - 1} λ^{n - k - 1} f (k) \end{array}$
よって

$λ \neq 0$ とする。漸化式 $a_{n + 1} = λ a_{n} + f (n)$ の一般解は
$a_{n} = C λ^{n} + \sum_{k = 0}^{n - 1} λ^{n - k - 1} f (k)$ ただし $C$ は任意定数で、 $n \geq 1$ とする。

が成り立ちます。

隣接３項間漸化式 $a_{n + 2} + p a_{n + 1} + q a_{n} = 0 (p, q \in C)$ の解

３項間漸化式なので $q \neq 0$ とします。
$λ^{2} + p λ + q = 0$ の解を $λ = α, β$ とすると、 $α \neq 0$ かつ $β \neq 0$ であり、
$\begin{array}{rcl} (S - α) (S - β) a_{n} & = & 0 \\ (S - β) a_{n} & = & \frac{1}{S - α} 0 \\ (S - β) a_{n} & = & C α^{n} \\ a_{n} & = & \frac{1}{S - β} (C α^{n}) \\ a_{n} & = & C^{'} β^{n} + C β^{n - 1} \sum_{k = 0}^{n - 1} {(\frac{α}{β})}^{n} \\ a_{n} & = & {\begin{matrix} C_{0} α^{n} + C_{1} β^{n} (α \neq β) \\ (C_{2} + C_{3} n) α^{n} (α = β) \end{matrix} \end{array}$
ただし $\begin{array}{r} C_{0} = \frac{C}{α - β}, C_{1} = C^{'} - C_{0}, C_{2} = C^{'}, C_{3} = \frac{C}{α} \end{array}$ とおいた。

漸化式 $(S - α) (S - β) a_{n} = 0$ の一般解は
$\begin{array}{r} a_{n} = {\begin{cases} C_{0} α^{n} + C_{1} β^{n} (α \neq β) \\ (C_{2} + C_{3} n) α^{n} (α = β) \end{cases} \end{array}$ ただし $C_{0}, C_{1}, C_{2}, C_{3}$ は任意定数

４項間以上のときも同様にすれば解を求めることができますが場合分けが少々面倒です。特殊解を使うともう少し簡単にできます。

特殊解を使った非同次線形漸化式の解法

漸化式 $a_{n + 1} = p a_{n} + q$ を解くとき、 $x = p x + q$ を満たす $x$ を求めて辺々引いて $(a_{n + 1} - x) = p (a_{n} - x)$ としました。この操作の利点は邪魔な定数 $q$ が消えて等比数列に帰着することでした。

いま、非同次線形漸化式 $f (S) a_{n} = g (n) \dots (1)$ が与えられていて、 $f (S) a_{n} = 0$ の一般解 $G_{n}$ （これを同次解と呼ぶことにします）がわかっているとします。ただし $f (S)$ は多項式です。特殊解を $a_{n} = P (n)$ とおくと $f (S) P (n) = g (n) \dots (2)$ であるので、式(1),(2)で辺々引いて $f (S) a_{n} - f (S) P (n) = 0$ すなわち $f (S) {a_{n} - P (n)} = 0$ となります。特殊解を用いることで邪魔だった $g (n)$ が消えて非同次漸化式を同次漸化式に帰着させることができました。よって、漸化式 $f (S) a_{n} = g (n)$ の一般解は
$\begin{array}{rcl} a_{n} - P (n) & = & G_{n} \\ a_{n} & = & P (n) + G_{n} \end{array}$
となります。特殊解と同次解の和です。

隣接３項間漸化式

$α \neq β$ とする。 $(S - β) a_{n} = C α^{n}$ の特殊解として $α^{n}$ の定数倍が思いつくと思います。 $a_{n} = C_{0} α^{n}$ としてみると $(S - β) a_{n} = (C_{0} α - C_{0} β) α^{n}$ となるので、 $\begin{array}{r} C_{0} = \frac{C}{α - β} \end{array}$ とすると $a_{n} = C_{0} α^{n}$ が特殊解になります。同次解は $C_{1} β^{n}$ であるので解は $a_{n} = C_{0} α^{n} + C_{1} β^{n}$ となります。

命題２の別証明

$a_{n} = \sum_{k = 0}^{n - 1} λ^{n - k - 1} f (k)$ とすると
$\begin{array}{rcl} (S - λ) a_{n} & = & \sum_{k = 0}^{n} λ^{n - k} f (k) - λ \sum_{k = 0}^{n - 1} λ^{n - k - 1} f (k) \\ = & (f (n) + \sum_{k = 0}^{n - 1} λ^{n - k} f (k)) - \sum_{k = 0}^{n - 1} λ^{n - k} f (k) \\ = & f (n) \end{array}$
であるから、これは特殊解である。同次解は $C λ^{n}$ であるから、
漸化式 $a_{n + 1} = λ a_{n} + f (n)$ の一般解は
$a_{n} = C λ^{n} + \sum_{k = 0}^{n - 1} λ^{n - k - 1} f (k)$

例２で急に特殊解を思いついていますが、次の事実によるものです。

$f (S)$ は多項式で、 $f (λ) \neq 0$ とする。漸化式 $f (S) a_{n} = λ^{n}$ に対して、
$a_{n} = \frac{1}{f (λ)} λ^{n}$
は特殊解である。

$f (S) = \sum_{i = 0}^{k} c_{i} S^{i}$ とおくと
$\begin{array}{rclrclrcl} f (S) λ^{n} & = & (\sum_{i = 0}^{k} c_{i} S^{i}) λ^{n} & = & \sum_{i = 0}^{k} c_{i} λ^{n + i} & = & (\sum_{i = 0}^{k} c_{i} λ^{i}) λ^{n} & = & f (λ) λ^{n} \end{array}$
となるから、
$f (S) (\frac{1}{f (λ)} λ^{n}) = \frac{1}{f (λ)} f (S) λ^{n} = \frac{1}{f (λ)} f (λ) λ^{n} = λ^{n}$

特殊解を分解して考えることもできます。

$f (S)$ を多項式とし、 $C_{i} (i = 1, 2, \dots, k)$ を定数とする。漸化式
$f (S) a_{n} = C_{1} g_{1} (n) + C_{2} g_{2} (n) + \dots + C_{k} g_{k} (n)$ の特殊解の１つ $P (n)$ は、 $f (S) a_{n} = g_{i} (n) (i = 1, 2, \dots, k)$ の特殊解を $a_{n} = P_{i} (n)$ とすると
$P (n) = C_{1} P_{1} (n) + C_{2} P_{2} (n) + \dots + C_{k} P_{k} (n)$ で与えられる。

$f (S) P_{i} (n) = g_{i} (n) (i = 1, 2, \dots, k)$
であるから、
$\begin{array}{rcl} f (S) (\sum_{i = 1}^{k} C_{i} P_{i} (n)) & = & \sum_{i = 1}^{k} C_{i} f (S) P_{i} (n) \\ = & \sum_{i = 1}^{k} C_{i} g_{i} (n) \end{array}$

漸化式 $(S - γ) a_{n} = C_{0} α^{n} + C_{1} β^{n} (α \neq γ, β \neq γ)$ の同次解は $C_{2} γ^{n}$ で、 $(S - γ) a_{n} = α^{n}, (S - γ) a_{n} = β^{n}$ の特殊解の１つとしてそれぞれ $\begin{array}{r} \frac{1}{α - γ} α^{n}, \frac{1}{β - γ} β^{n} \end{array}$ が取れるので、一般解は $a_{n} = C_{3} α^{n} + C_{4} β^{n} + C_{2} γ^{n}$ である。ただし $\begin{array}{r} C_{3} = \frac{C_{0}}{α - γ}, C_{4} = \frac{C_{1}}{β - γ} \end{array}$ とおいた。

定数係数同次線形漸化式の解法その2

特性方程式

$f (S)$ を多項式とする。漸化式
$f (S) a_{n} = 0$
に対して、方程式
$f (λ) = 0$
をこの漸化式の特性方程式という。

x = p x + q

僕が持っている参考書の中には、 $a_{n + 1} = p a_{n} + q$ に対して $x = p x + q$ を特性方程式という、と書かれているものがありましたが２項間のときだけ定義を変えるのも変なので、ここでは $x = p x + q$ は特性方程式と呼ばないことにします。（高校の教科書を確認したところ、そもそも特性方程式という言葉は出てきていませんでした。）

特性方程式が重解を持たない場合

例４では特性方程式が重解を持たないような定数係数隣接４項間同次線形漸化式の一般解を求めています。

例４のように補題３と補題４を使うことで、特性方程式が重解を持たないようなような定数係数隣接 $k$ 項間同次線形漸化式の一般解なら求めることができます。

$f (S)$ は重根を持たない $k$ 次多項式とする。方程式 $f (λ) = 0$ の異なる $k$ 個の解を $λ = λ_{i} (i = 1, 2, \dots, k)$ とすると、漸化式 $f (S) a_{n} = 0$ の一般解は
$a_{n} = C_{1} λ_{1}^{n} + C_{2} λ_{2}^{n} + \dots + C_{k} λ_{k}^{n}$
である。 $C_{i} (i = 1, 2, \dots, k)$ は任意定数とする。

全ての自然数 $k$ で成り立つことを数学的帰納法で示す。
[1] $k = 1$ の場合は前に証明しているので省略します。
[2] $k = m (m \geq 1)$ で成り立つと仮定すると、
$(S - λ_{1}) (S - λ_{2}) \dots (S - λ_{m}) a_{n} = 0$ の一般解は
$a_{n} = C_{1} λ_{1}^{n} + C_{2} λ_{2}^{n} + \dots + C_{m} λ_{m}^{n}$ であるから、
$(S - λ_{1}) (S - λ_{2}) \dots (S - λ_{m}) (S - λ_{m + 1}) a_{n} = 0$ は
$(S - λ_{m + 1}) a_{n} = C_{1} λ_{1}^{n} + C_{2} λ_{2}^{n} + \dots + C_{m} λ_{m}^{n} \dots (A)$
と変形できる。同次解は $C_{m + 1} λ_{m + 1}^{n}$ である。
補題３から、 $(S - λ_{m + 1}) a_{n} = λ_{i}^{n} (i = 1, 2, \dots, m)$ の特殊解は
$a_{n} = \frac{1}{λ_{i} - λ_{m + 1}} λ_{i}^{n}$ で与えられるから、補題４より $(A)$ の一般解は
$a_{n} = C_{1}^{'} λ_{1}^{n} + C_{2}^{'} λ_{2}^{n} + \dots + C_{m}^{'} λ_{m}^{n} + C_{m + 1} λ_{m + 1}^{n} (C_{i}^{'} = \frac{C_{i}}{λ_{i} - λ_{m + 1}})$
である。よって $k = m + 1$ でも成り立つ。
[1],[2]より、全ての自然数 $k$ で成り立つ。

途中で $\begin{array}{r} \frac{1}{λ_{i} - λ_{m + 1}} \end{array}$ が出てきているので $f (S)$ が重解を持つときは残念ながらこの方法は使えません。

特性方程式が重解を持つ場合

まずは次の等式を証明します。（ $Δ = S - 1$ です。）

$k$ は自然数の定数とする。
$(S - λ)^{k} a_{n} = λ^{n + k} Δ^{k} (λ^{- n} a_{n})$ ただし $λ \neq 0$ とする。

二項係数は $\begin{array}{r} (\binom{n}{k}) \end{array}$ $(=_{n} C_{k})$ で書きます。
$\begin{array}{rcl} (S - λ)^{k} a_{n} & = & \sum_{i = 0}^{k} (\binom{k}{i}) (- λ)^{k - i} S^{i} a_{n} \\ = & \sum_{i = 0}^{k} (\binom{k}{i}) (- 1)^{k - i} λ^{k - i} a_{n + i} \\ = & λ^{n + k} \sum_{i = 0}^{k} (\binom{k}{i}) (- 1)^{k - i} \frac{a_{n + i}}{λ^{n + i}} \\ = & λ^{n + k} \sum_{i = 0}^{k} (\binom{k}{i}) (- 1)^{k - i} S^{i} \frac{a_{n}}{λ^{n}} \\ = & λ^{n + k} (S - 1)^{k} \frac{a_{n}}{λ^{n}} \\ = & λ^{n + k} Δ^{k} (λ^{- n} a_{n}) \end{array}$

これを使って $(S - λ)^{k} a_{n} = 0$ の一般解を求めると、
$\begin{array}{rcl} (S - λ)^{k} a_{n} & = & 0 \\ λ^{n + k} Δ^{k} (λ^{- n} a_{n}) & = & 0 \\ Δ^{k} (λ^{- n} a_{n}) & = & 0 \end{array}$
であるので
$\begin{array}{rcl} Δ^{k - 1} (λ^{- n} a_{n}) & = & C_{0} \\ Δ^{k - 2} (λ^{- n} a_{n}) & = & C_{1} + C_{2} n \\ ⋮ \end{array}$
$\begin{array}{rcl} λ^{- n} a_{n} & = & C_{0}^{'} + C_{1}^{'} n + C_{2}^{'} n^{2} + \dots + C_{k - 1}^{'} n^{k - 1}) \\ a_{n} & = & (C_{0}^{'} + C_{1}^{'} n + C_{2}^{'} n^{2} + \dots + C_{k - 1}^{'} n^{k - 1}) λ^{n} \end{array}$

ここで、命題2と $\begin{array}{r} \sum_{i = 0}^{n} i^{k} \end{array}$ は $n$ の $k + 1$ 次式で表されることを用いています。また、その式は $n = 0$ を代入すると0になるので、 $n = 0$ のときも成り立ちます。

よって、

$k$ は自然数の定数とする。漸化式 $(S - λ)^{k} a_{n} = 0$ の一般解は
$a_{n} = (C_{0} + C_{1} n + C_{2} n^{2} + \dots + C_{k - 1} n^{k - 1}) λ^{n}$
ただし $λ \neq 0$ であり、 $C_{i} (i = 0, 1, \dots, k - 1)$ は任意定数とする。

そして、次が成り立ちます。

$λ \neq 0, 1$ とし、漸化式 $(S - λ)^{m} a_{n} = 0$ の解を $G (λ, m)$ とする。任意の $\begin{array}{r} f (n) \in G (λ, m) \end{array}$ に対して、漸化式 $Δ^{k} a_{n} = f (n)$ の特殊解であって $G (λ, m)$ に属するものがただ１つ存在し、逆に、任意の $\begin{array}{r} g (n) \in G (λ, m) \end{array}$ に対して $Δ^{k} g (n) \in G (λ, m)$ となる。

$\begin{array}{r} g (n) \in G (λ, m) \end{array}$ ならば $g (n) = (C_{0} + C_{1} n + C_{2} n^{2} + \dots + C_{m - 1} n^{m - 1}) λ^{n}$ とおけて、
$\begin{array}{rcl} Δ g (n) & = & (C_{0} + C_{1} (n + 1) + C_{2} (n + 1)^{2} + \dots + C_{m - 1} (n + 1)^{m - 1}) λ^{n + 1} - (C_{0} + C_{1} n + C_{2} n^{2} + \dots + C_{m - 1} n^{m - 1}) λ^{n} \\ = & (C_{0} λ - C_{0} + C_{1} λ (n + 1) - C_{1} n + C_{2} λ (n + 1)^{2} - C_{2} n^{2} + \dots + C_{m - 1} λ (n + 1)^{m - 1} - C_{m - 1} (n + 1)^{m - 1}) λ^{n} \end{array}$
であるので、常に $\begin{array}{r} Δ g (n) \in G (λ, m) \end{array}$
また、 $i$ 次の係数は $C_{j} (j = i, i + 1, \dots, m - 1)$ で表されるので、任意の $\begin{array}{r} f (n) \in G (λ, m) \end{array}$ で $Δ g (n) = f (n)$ となるような定数 $C_{i} (i = 0, 1, \dots, k - 1)$ は一意に決定される。
これを $k$ 回繰り返せば、題意が従う。

これで準備は整いました。

$k$ は自然数の定数とする。漸化式
$(S - λ_{1})^{m_{1}} (S - λ_{2})^{m_{2}} \dots (S - λ_{k})^{m_{k}} a_{n} = 0$ の一般解は
$a_{n} = \sum_{i = 1}^{k} (λ_{i}^{n} \sum_{j = 0}^{m_{i} - 1} C_{i, j} n^{j})$
である。ただし $λ_{i} (i = 1, 2, \dots, k)$ は0でない相異なる実数であり、 $m_{i} (i = 1, 2, \dots, k)$ は正の整数であり、 $C_{i, j}$ は任意定数とする。

全ての自然数 $k$ で成り立つことを数学的帰納法で示す。
[1] $k = 1$ のときは補題7より成立する。
[2] $k = N (\geq 1)$ で成り立つと仮定すると、
$(S - λ_{1})^{m_{1}} (S - λ_{2})^{m_{2}} \dots (S - λ_{N})^{m_{N}} a_{n} = 0$ の一般解は $a_{n} = \sum_{i = 1}^{N} (λ_{i}^{n} \sum_{j = 0}^{m_{i} - 1} C_{i, j} n^{j})$ であるから、 $(S - λ_{1})^{m_{1}} (S - λ_{2})^{m_{2}} \dots (S - λ_{N})^{m_{N}} (S - λ_{N + 1})^{m_{N + 1}} a_{n} = 0 \dots (B)$ は $(S - λ_{N + 1})^{m_{N + 1}} a_{n} = \sum_{i = 1}^{N} (λ_{i}^{n} \sum_{j = 0}^{m_{i} - 1} C_{i, j} n^{j})$ と変形できる。これの同次解は $λ_{N + 1}^{n} \sum_{j = 0}^{m_{N + 1} - 1} C_{N + 1, j} n^{j}$ である。
ここで、 $(S - λ_{N + 1})^{m_{N + 1}} a_{n} = λ_{i}^{n} \sum_{j = 0}^{m_{i} - 1} C_{i, j} n^{j} (i = 1, 2, \dots, m) \dots (C)$ は補題6より $\begin{array}{rcl} λ_{N + 1}^{n + m_{N + 1}} Δ^{m_{N + 1}} (λ_{N + 1}^{- n} a_{n}) & = & λ_{i}^{n} \sum_{j = 0}^{m_{i} - 1} C_{i, j} n^{j} \\ Δ^{m_{N + 1}} (λ_{N + 1}^{- n} a_{n}) & = & λ_{N + 1}^{m_{N + 1}} {(\frac{λ_{i}}{λ_{N + 1}})}^{n} \cdot \sum_{j = 0}^{m_{i} - 1} C_{i, j} n^{j} \dots (D) \end{array}$ と変形でき、補題7より、漸化式 $(S - λ)^{m} a_{n} = 0$ の一般解を $a_{n} = g (λ, m)$ とすると、 $g (\frac{λ_{i}}{λ_{N + 1}}, m_{i}) = {(\frac{λ_{i}}{λ_{N + 1}})}^{n} \cdot \sum_{j = 0}^{m_{i} - 1} C_{i, j} n^{j}$ であるので、 $Δ^{m_{N + 1}} (λ_{N + 1}^{- n} a_{n}) = g (\frac{λ_{i}}{λ_{N + 1}}, m_{i}) \dots (E)$
よって補題8より、 $(E)$ の特殊解であって $\begin{array}{r} G (\frac{λ_{i}}{λ_{N + 1}}, m_{i}) \end{array}$ に属するものが存在するから、適切に定数 $C_{i, j}^{'}$ を取って、 $λ_{N + 1}^{- n} a_{n} = {(\frac{λ_{i}}{λ_{N + 1}})}^{n} \sum_{j = 0}^{m_{i} - 1} C_{i, j}^{'} n^{j}$ とすれば、これは(E)を満たす。また、補題8より、 $C_{i, j}^{'}$ は任意定数としてよい。
ゆえに、 $λ_{i}^{n} \sum_{j = 0}^{m_{i} - 1} C_{i, j}^{'} n^{j}$ が(C)の特殊解となるので、補題4より、 $\sum_{i = 1}^{N} (λ_{i}^{n} \sum_{j = 0}^{m_{i} - 1} C_{i, j}^{'} n^{j})$ は(B)の特殊解となるから、(B)の一般解は、 $a_{n} = λ_{N + 1}^{n} \sum_{j = 0}^{m_{N + 1} - 1} C_{N + 1, j} n^{j} + \sum_{i = 1}^{N} (λ_{i}^{n} \sum_{j = 0}^{m_{i} - 1} C_{i, j}^{'} n^{j})$ である。
$C_{N + 1, j} = C_{N + 1, j}^{'}$ とおけば、 $a_{n} = \sum_{i = 1}^{N + 1} (λ_{i}^{n} \sum_{j = 0}^{m_{i} - 1} C_{i, j}^{'} n^{j})$ よって $k = N + 1$ でも成り立つ。
[1],[2]より、全ての自然数 $k$ で成り立つ。

これですべての定数係数隣接 $k$ 項間同次線形漸化式の一般解を求めることができるようになりました！

命題9で $m_{i} = 1 (i = 1, 2, \dots, k)$ とすると、
$(S - λ_{1}) (S - λ_{2}) \dots (S - λ_{k}) a_{n} = 0$ の一般解は
$a_{n} = \sum_{i = 1}^{k} C_{i} λ_{i}^{n}$
となり、これは命題5の結果と一致する。

漸化式 $(S - α)^{p} (S - β)^{q} a_{n} = 0$ ( $α \neq β$ 、 $p, q$ は正の整数)の一般解は
$a_{n} = (C_{1, 0} + C_{1, 1} n + \dots + C_{1, p - 1} n^{p - 1}) α^{n} + (C_{2, 0} + C_{2, 1} n + \dots + C_{2, q - 1} n^{q - 1}) β^{n}$ である。

2005年の東京医科歯科大学の数学入試問題の第１問（２）です。

(2)次のように定義される数列 ${b_{n}}$ の一般項を求めよ。
$b_{1} = 2, b_{2} = \frac{5}{2}, b_{3} = \frac{17}{4}$
$b_{n} = \frac{7}{2} b_{n - 1} - \frac{7}{2} b_{n - 2} + b_{n - 3} (n = 4, 5, 6, \dots)$

まず一般解を求めます。

$\begin{array}{rcl} b_{n} = \frac{7}{2} b_{n - 1} - \frac{7}{2} b_{n - 2} + b_{n - 3} \\ b_{n + 3} - \frac{7}{2} b_{n + 2} + \frac{7}{2} b_{n + 1} - b_{n} & = & 0 \\ (S^{3} - \frac{7}{2} S^{2} + \frac{7}{2} S - 1) b_{n} & = & 0 \\ (S - \frac{1}{2}) (S - 1) (S - 2) b_{n} & = & 0 \\ b_{n} = C_{1} {(\frac{1}{2})}^{n} + C_{2} + C_{3} 2^{n} \end{array}$
ここで $C_{1}, C_{2}, C_{3}$ は定数とする。

次に初期条件から一般項を求めます。

$b_{1} = 2, b_{2} = \frac{5}{2}, b_{3} = \frac{17}{4}$ より、
$\begin{array}{r} {\begin{cases} \frac{1}{2} C_{1} + C_{2} + 2 C_{3} = 2 \\ \frac{1}{4} C_{1} + C_{2} + 4 C_{3} = \frac{5}{2} \\ \frac{1}{8} C_{1} + C_{2} + 8 C_{3} = \frac{17}{4} \end{cases} \end{array}$
これを解いて、 $C_{1} = 2, C_{2} = 0, C_{3} = \frac{1}{2}$
よって、 $b_{n} = {(\frac{1}{2})}^{n - 1} + 2^{n - 1}$

非同次の線形漸化式を解くには特殊解を1つ見つける必要がありますが、その詳しい求め方に関しては、また時間のあるときに調べてみようと思います。

投稿日：2023年3月15日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

Omicron

1636

オミクロン株出てくる前からこの名前でした。

他の人のコメント

コメントはありません。

読み込み中

Omicron

定数係数線形漸化式の演算子的解法

演算子$S$の導入
定数係数同次線形漸化式の解法その１
隣接２項間漸化式$a_{n+1}=\lambda a_n+f(n)(\lambda\in\mathbb{C} \verb|\| \{0\})$の解
隣接３項間漸化式$a_{n+2}+pa_{n+1}+qa_n=0(p,q\in\mathbb{C})$の解
特殊解を使った非同次線形漸化式の解法
定数係数同次線形漸化式の解法その2
特性方程式が重解を持たない場合
特性方程式が重解を持つ場合

定数係数線形漸化式の演算子的解法

演算子Sの導入

定数係数同次線形漸化式の解法その１

隣接２項間漸化式an+1=λan+f(n)(λ∈C\{0})の解

f(n)=0のとき

λ=1のとき

an+1=λan+f(n)の解

隣接３項間漸化式an+2+pan+1+qan=0(p,q∈C)の解

特殊解を使った非同次線形漸化式の解法

定数係数同次線形漸化式の解法その2

特性方程式が重解を持たない場合

特性方程式が重解を持つ場合

まず一般解を求めます。

次に初期条件から一般項を求めます。

この記事を高評価した人

この記事に送られたバッジ

投稿者

コメント

他の人のコメント

演算子 $S$ の導入

隣接２項間漸化式 $a_{n + 1} = λ a_{n} + f (n) (λ \in C \ {0})$ の解

$f (n) = 0$ のとき

$λ = 1$ のとき

$a_{n + 1} = λ a_{n} + f (n)$ の解

隣接３項間漸化式 $a_{n + 2} + p a_{n + 1} + q a_{n} = 0 (p, q \in C)$ の解